“减负增效”背景下初中数学作业设计策略研究
2023-10-07林秀玉福建省平潭县城关中学强兴校区350400
林秀玉 (福建省平潭县城关中学强兴校区 350400)
怎样提高作业布置的“有效性”,促使学生在有限的课后时间内达成知识巩固、拓展提升的目标,实现任务和负担之间的“平衡”,就成为一个非常现实的话题。
一、“减负增效”背景下的初中数学作业设计要求
1.巩固提升,以完成基础知识学习为导向
作业是对课堂教学内容的有力补充,需要以巩固基础知识、整合知识网络为根本目标,可以被细化为学习理解、实践应用、创新迁移三个阶段。“减负增效”的提出,意味着对“作业量”直接打了“折扣”,初中数学教师仍需要将作业布置的基点置于巩固层面,让学生在复习总结、应用锻炼中,间接达到提升知识应用效率和熟练度的目的。
2.拓展丰富,以发展核心素养为目标
事实证明,要想提高学生对数学知识的理解和应用能力,不断发展核心素养,就需要基于一定的展示平台、数学情境.数学作业刚好就是这样的“舞台”,教师可以在作业设置时,利用具有一定的开放性、拓展性以及探究性的内容,引导学生发散思维、整合知识点,提高理论联系实际能力。
3.分层试练,以实现个性成长为原则
作业布置的四大关键点在于规范、数量、质量以及形式,任何时期、任何政策之下,学生个体发展都必然存在着差异性。坚持因材施教、个性发展,是“双减”背景下实施“减负增效”所绕不开的一个话题。根据新课程标准要求,初中数学教师在课后布置数学作业,强调分层试练,本身就是尊重学生个性所做出的选择。
二、“减负增效”背景下的初中数学作业设计实践
1.巩固性作业
“双减”政策明确指出,要“发挥作业诊断、巩固、学情分析等功能”,所以巩固性作业设置的关键在于生成高质量的、基础性作业类型且辐射全班不同层次学生。巩固性作业要求教师基于新课程标准,结合数学学科特点,坚持多个作业类型(基础的背诵和习题练习、跨学科作业、综合实践性作业等)的“整合”。
举例来说,初中一年级利用一元一次方程解决实际问题这部分内容,对于很多学生而言,难点在于如何寻找题目当中潜在的等量关系。因此,在课后进行作业设置,笔者设置了若干个可以通过一元一次方程解决问题的场景,让学生寻找其中潜在的等量关系,不以解题或者列出方程式为作业要求。如例题:
已知某企业为严重缺水的甲、乙两所学校捐赠矿泉水共计2000件,其中捐赠给甲学校的矿泉水数量是乙矿泉水数量的2倍少400件,分别求该企业为两所学校各自捐赠了多少件矿泉水。
可以发现,题目当中包含着两种等量关系,一是两个学校共同捐赠的矿泉水数量之和“等于”2000,二是捐赠给甲学校的矿泉水数量“等于”乙矿泉水数量的2倍少400件。这意味着后期在使用方程求解过程中,列出方程式的方式至少有两种。
学生会逐渐发现,等量关系的寻找往往在题目当中有着较为清晰的隐藏字样,如“……等于……”“……是……的”“由……组成”“包括……”等。当学生接触到一定量的题目后,可以对其进行内容要素的类型分解,进而把握“一元一次方程解决实际问题”的潜在性规律。
2.拓展性作业
拓展性作业,需要教师向学生布置具有开放性的作业,让学生展开想象、发散思维,完成作业。以这样一道平行四边形题目为例:
▱ABCD的对角线AC,BD相交于点O(如图1所示),EF过点O且与AD,BC分别相交于点E,F,则OE=OF。若将EF向两方延长与平行四边形的两对边的延长线分别相交(图2和图3),OE与OF还相等吗? 若相等,请说明你的理由。
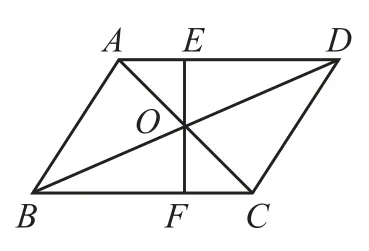
图1
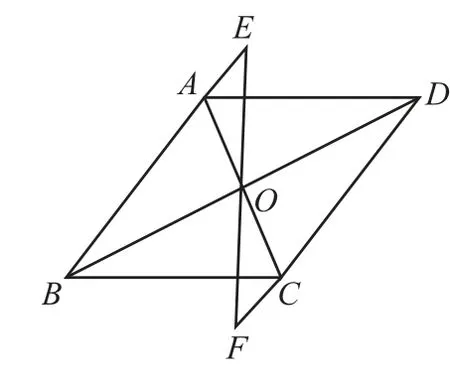
图2

图3
要想证明OE与OF相等,可以通过创造全等三角形的方式进行求解。解题过程,是对学生课堂所学基础性知识(包括平行四边形的性质、全等三角形的判定方法)的巩固。以此为基础,对这道题进行变式,可以得到这样一道题目:
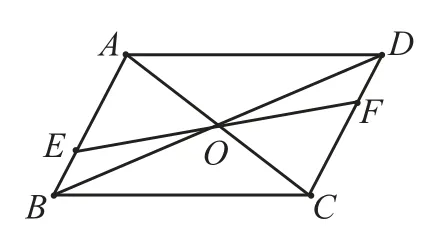
如图,在四边形ABCD中,AB//CD,对角线AC,BD相交于点O,EF过点O交AB于点E,交CD于点F,且OE=OF。
(1)求证:四边形ABCD是平行四边形;
(2)若S四边形AEFD=5,则S四边形ABCD=________。
不难发现这道题目是对前一题目的变式和升级,考验的是学生逆向思维能力,应用到平行四边形的判定方法。在考查基础知识的前提下,题目对四边形面积的计算考验的是学生思维转换能力。此时,如果学生单纯去考虑套用平行四边形的面积公式进行计算,很有可能陷入“僵局”。此题的关键就在于从单纯的求解图形的面积转变为判断其与已知图形之间的关系,进而得出相应答案。
而综合前两道题的命题思路和考查要点,可以通过对题目已知条件和位置条件进行适度调整和改变,让题目本身具有开放性,并且起到启迪学生思维,培养其探究意识的效果。
如图4,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O与AB,CD分别相交于点E,F,(1)求证:OE=OF;

图4
(2)若上图中的条件都不变,将EF转动到图5的位置,那么上述结论是否成立?
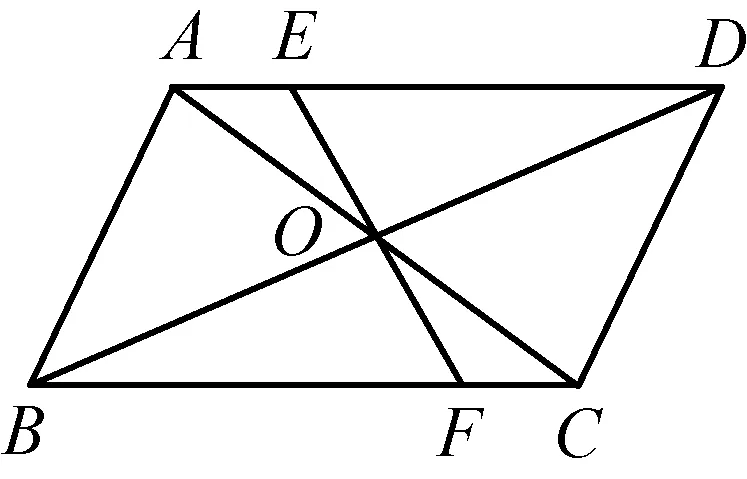
图5
(3)若将EF向两方延长与平行四边形的两对边的延长线分别相交(图6 和图7),结论是否成立,说明你的理由。
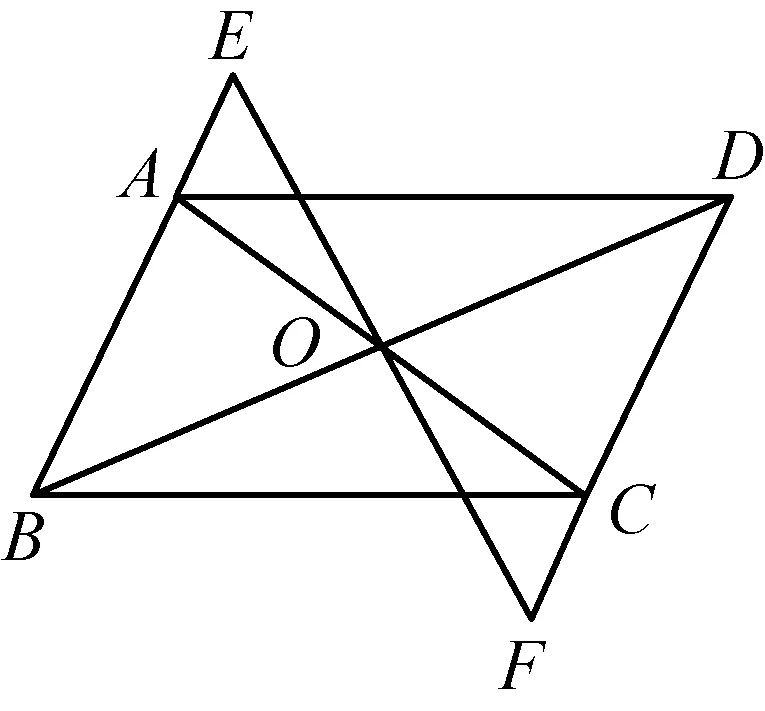
图6
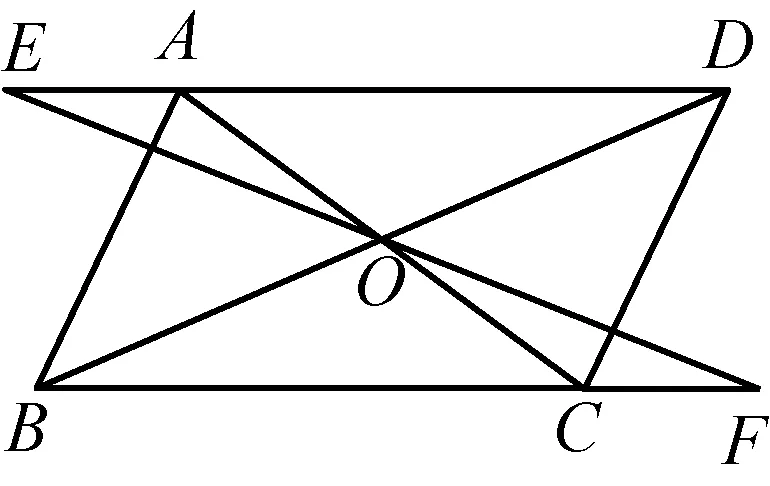
图7
相对于上两种提出明确问题的试题,最新一道题目的特点在于其问题指向的不明确性,即带有开放性特征,需要学生自行进行猜测、自行进行求解和证明。如果同时将这三道题布置给学生,感受学生思维从按部就班到逐渐开放的过程,学生探究能力会得到显著提升。
3.分层式作业
分层作业的实施目标在于,将全班同学划分为学困、中档以及良好三个类别,针对性设置作业,确保所有学生都有所得。
以九年级下册学习到的锐角三角函数为例,因为Rt三角形当中,锐角的三角函数计算有着清晰的公式,根据角的边长、度数等信息已知程度的不同,直接将问题难度划分为不同层次,正好可以辐射初中数学三种不同学习状态学生。
首先,对于学习困难的学生,可以进行基础锐角三角函数知识的巩固和简单计算。比如,已知在Rt△ABC当中,∠C=90°,BC=4、AB=5,求cosB的值。根据锐角三角形的三角函数计算公式可知,直角三角形中,某锐角的余弦函数等于邻边与对边的比值,此时根据题目已知条件,就可以达到轻松求解的目的;同理,教师可以根据这种题目类型衍生出很多变式,保证本身对数学学习感到压力的学生,能够基于已有条件,巩固概念和知识,并完成基本求解。
其次,对于中档的学生,教师需要为学生设置障碍,让学生通过更多步骤灵活调度自己学习过的知识,进而达到解决问题的目的。比如,已知在Rt△ABC当中,∠C=90°,,则cosB的值为_________。相对于之前的提问,这一类型题目的特点在于没有将能够直接用来求解的条件摆放在学生面前(简单套公式就可以求解),而是让学生进行二次计算,根据求解判断所需要的已知。
最后,对于良好的学生,作业设置要尽可能激发其数学思维,巩固和不断提升其数学思想,确保其能够在既定内容中挖掘潜在信息,甚至判断出命题意向、动机。比如,已知在Rt△ABC当中,∠C=90°,CD是高,在AC=4、AD=3的情况下,求解cosB。很明显,这道题融入了三角函数和勾股定理知识,需要学生对过往学习过的相关知识进行系统性整合以及应用。后期随着学生所学知识不断丰富,这道题目还可以融入包括相似三角形、转化法等多种角度进行求解,对学生思维能力拓展是不小考验。
三、“减负增效”背景下的初中数学作业评价与反馈
1.通过作业评价与反馈,实现为学生“减负”的目的
针对学生上交的,最终以书写形式呈现的作业,需要教师做到及时批改以及精细化批改。前者的目的是为了及时纠正学生通过作业表现出的问题、错误,防止不正确的观念被进一步带到下一阶段学习中;后者则需要教师针对学生作业思路、书写规范等连带性的内容进行批改,让学生快速从教师批改的印记中了解思路错误的原因,既懂得如何去思考,也懂得如何规范解题。
2.“双主体”的作业评价与反馈
“双主体”的作业评价与反馈意味着改变过往单纯由教师主导的作业评价和批改方式,强调学生也可以进行批改,成为评价与反馈工作的主体。教师和学生具体的评价重点必然有所不同,学生需要结合教师所制定的评价标准(如结果的正确与否、书写是否规范、步骤是否正确和清晰)进行对标评价;教师针对学生作业进行的评价属于过程性、原因性评价,需要对问题产生原因进行剖析,需要对学生解决问题的思路进行研究,同时做好问题整改及优秀学习方法的推介和分享。如此,学生主体地位得到进一步提升,对提高其学习积极性会产生良好促进作用。
