对小学生数形结合能力现状的调查与教学建议

李杲

［摘 要］教材中有大量数形结合的身影，通过分析学生习题检测结果，结合调查与访谈发现，受传统教学观念与教学方式的影响，部分教师对数形结合思想没有足够的重视，导致学生经验欠缺，运用能力不足。结合实际情况，建议教师在教学过程中转变观念，认真研读课程标准和教材，采用“以形助数”“以数解形”“数形互助”等学习策略，丰富数形结合思想的教学资源。

［关键词］小学数学； 数形结合；调查；分析；策略

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）20-0028-04

一、問题的缘起

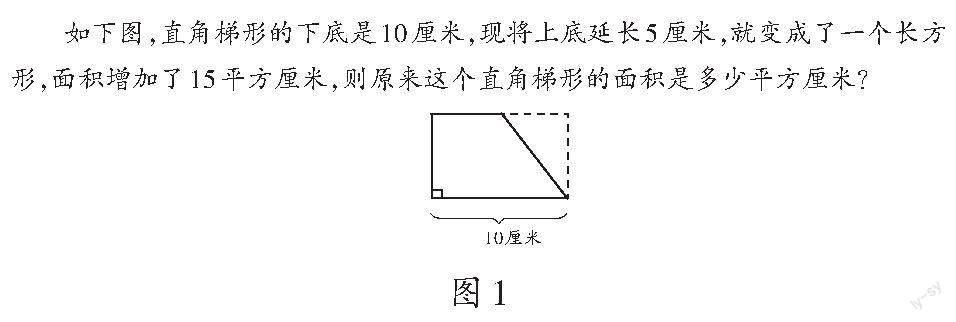
在我校五年级“多边形的面积”单元的学生作业中，一名学生解答题目 “有一个直角梯形，它的下底是12厘米，现将上底延长5厘米，就变成了一个长方形，面积增加了15平方厘米，原来这个直角梯形的面积是多少平方厘米？”的方法让笔者产生了疑虑。

这道题考查的是学生是否能运用数形结合思想画图解决问题。可是，这道题目的正确率只有76.31%，且尝试运用数形结合思想解决问题的学生只占52.63%。这是本班的个例，还是五年级学生的普遍现象？带着这个疑问，笔者调查并统计了本校五年级5个班和另一所学校五年级3个班的学生答题情况，结果见表1。

分析发现，无论是本校还是外校，运用数形结合思想解题的学生人数所占比例均不足70%，甚至出现50%的比例。为了更深入地了解学生对数形结合思想的认识的现状，笔者决定从教材、学生、教师三方面着手进行调查分析。

二、调查设计与调查过程

1.对教材的调查

数形结合思想在教材知识体系中是如何呈现的？笔者翻阅人教版教材时发现，在教学“乘法分配律”时，渗透的重要思想就是数形结合思想。教材引导学生采用不完全归纳法发现规律，启发学生用自己喜欢的方式表示规律，并突出要求“用图形、字母和其他符号表示规律”，针对a×（b+c）=a×b+a×c这种形式，说一说a和b可以表示什么数，以促使学生深入理解分配律的内涵。可以看出，在四、五年级的教材中，教材编者注重数形结合思想的渗透和应用。

2.题组训练跟进调查

在跟进调查中，笔者决定更改题目数据，并给出相应图形（如图1），以检测学生的正确率是否有提高。

检测发现，学生的正确率大大提高，可见运用数形结合思想确实可以帮助学生提高解决问题的能力。之前答错的大部分学生在解这题时都能够根据图来说明思考过程。

3.问卷调查

问卷内容 （学生版）：

（1）你听说过数形结合思想吗？如果听说过，请用你喜欢的方式描述出来。

（2）你的数学老师经常在教学中应用数形结合思想吗？

（3）你会主动运用数形结合思想解决问题吗？说出你的理由。

对于第（1）题，有90.5%的学生表示听说过数形结合思想。其中有11.5%的学生认为数形结合思想是代数知识，有22.8%的学生认为数形结合思想是几何知识，有39.5%的学生认为数形结合思想既是代数知识又是几何知识，有11.5%的学生认为数形结合思想通过代数知识研究几何知识和通过图示来理解数学知识。

对于第（2）题，有47.2%的学生表示教师上课时经常运用数形结合思想来教学，有21.5%的学生表示老师偶尔运用数形结合思想来教学。

对于第（3）题，有56.9%的学生表示自己会主动运用数形结合思想来学习，因为通过图示可以提升解决问题的速度；有31.7%的学生表示自己偶尔会运用数形结合思想来解题，因为有时候画图比较麻烦，也不知道该怎么画出清晰的图示。

问卷内容 （教师版）：

（1）你认为数形结合思想重要吗？

（2）教学中，你经常向学生提及数形结合思想吗？

（3）对于运用数形结合思想解题的学生，你会怎么做？

（4）人教版教材哪些章节中出现过“数形结合”的模型？（至少5 个）

对于第（1）题，100%的教师认为数形结合思想对数学教学很重要。

对于第（2）题，67.1%的教师表示上课时经常运用数形结合思想来教学，32.9%的教师表示偶尔运用数形结合思想来教学。

对于第（3）题，32.6%的教师表示会积极表扬运用数形结合思想来思考的学生，45.9%的教师表示偶尔会表扬运用数形结合思想来思考的学生。

对于第（4）题，63.7%的教师能够说出5个以上的模型，27.3%的教师能说出10个以上的模型。

三、原因分析

从学生、教材、教师三方面的调查结果可以看出，促进学生运用数形结合思想来解决问题，看似简单，实则是一大难题。

首先，如果教师没有积极转变教学理念，学生对数形结合思想的认识就不会很清晰。其次，对于数形结合思想的运用方法，如果教师教学不够灵活、系统，不知道如何引导学生，学生在学习数学的过程中就不能体会到运用数形结合思想解决问题的便利，从而丧失积极思考、寻求突破的兴趣。

四、教学建议

1.“以形助数”，培育沃土

“以形助数”是指借助图形的直观特点，促进学生理解抽象概念的数、数量和数量关系，帮助学生精准掌握并运用数学知识。

（1）借助实物，感受数的内涵

运用数形结合思想能够将题目信息转化成对应的图形或直观符号，促进学生建构数与形之间的关系，引导学生深入思考问题并解决问题，进而使学生归纳出“形”对“数”的帮助。

例如，对于“体积和体积单位”，有些学生对体积的概念掌握熟练，却对具体实物的体积大小判断出现差错，这有可能是因为教师在教学时没有将体积单位和所对应的实物进行联系。因此，教师在教学时可先通过乌鸦喝水的情境导入，引导学生在讨论和交流中感悟有关体积的表象；再让学生通过观察、比较实验过程中的现象，概括体积的概念，并比较不同物体的体积大小；最后引出体积单位的学习，引导学生根据长度单位和面积单位的学习经验进行类推，进而想到比较体积大小同样需要一个统一的体积单位作为标准。此外，教师还可以借助直观的教具进行演示，或利用学生熟知的物体，引导学生将体积单位和生活实物进行联系（如图2），让学生通过观察对比建立清晰的表象。

建构完体积单位的模型后，教师让学生思考生活中的物品可以用哪些体积单位来度量，并完成练习（如图3）。

（2）依托线段图或实物，简化抽象问题

①借助线段图理解数学问题

线段图能将抽象的数量关系直观化。在教学中，教师可以引导学生感悟线段的妙用，培养学生运用数形结合思想解决问题的能力。

例如，学习“植树问题”时，学生受到负迁移的影响，解决简单问题的时候更容易出错。

对于题目“同学们在全长40米的小路一边上植树，每隔8米栽一棵（两端要栽），一共需要栽多少棵树？”，学生一看到题目就会觉得答案是40÷8=5（棵）。显然，这个答案是错误的。此时，教师要指导学生画线段图（如图4），把分割的点数和棵数进行一一对应，帮助学生发现两端都栽的情况下，棵数=间隔数+1，进而延伸一端栽一端不栽和两端都不栽的情况的规律，以此丰富“植树问题”的数学模型。

②借助实物，理解算理和算法

要掌握计算的知识与技巧，关键在于建构算理和算法模型。

例如，在教学“两位数除以一位数”时，对于48÷3，笔者借助实物——小棒，使计算具体化：先在3个方框中分10根小棒，再把剩下的18根小棒平均分到3个方框中（如图5）。

2.“以数解形”，厚积薄发

在小学阶段，学生对平面图形的学习是建立在实物之上的，而组合图形的面积的学习又是建立在平面图形的学习之上的。因此，引导学生对比、分析、建构，可以帮助学生归纳图形之间的联系。

例如，在回顾多边形的面积公式时，教师可引导学生对学过的图形进行归纳，了解它们之间的联系，将脑海中的知识碎片归整成块（如图6）。

当学生掌握了图形之间的转化之后，便能发现梯形与平行四边形和三角形之间的图形联系（如图7）。

经历这两个活动后，学生进一步加深了对图形面积公式的理解，深化了几何直观。

3.“数形互助”，融会贯通

（1）挖掘“数”与“形”内在联系，构造图像

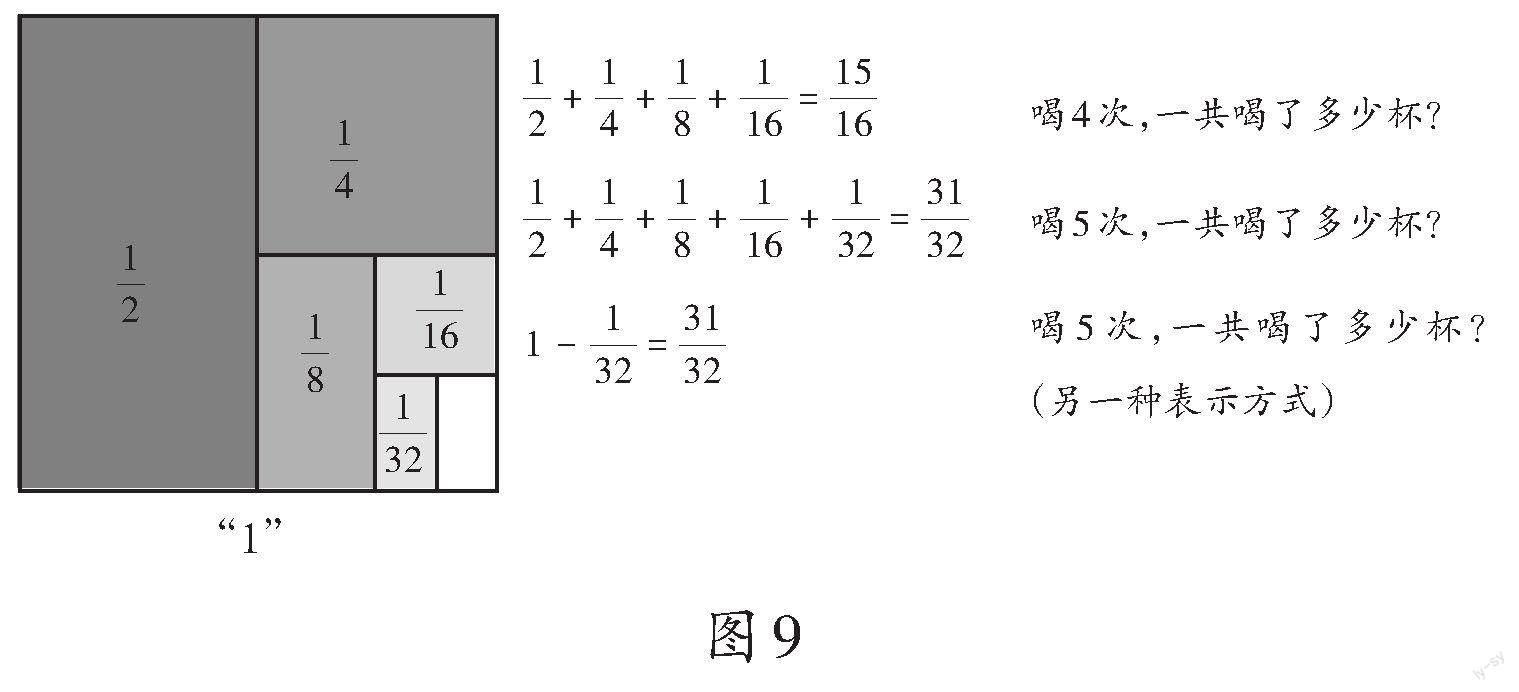
在五年级的学习中，“喝牛奶問题”是一个典型的数形结合例子，对学生来说是一个难点。为突破这个难点，教师需要引导学生在解决问题的过程中画图示，建构出纯牛奶模型，让图示发挥在题意理解、数量分析和问题解决上的优势，提升学生的几何直观素养。

教师在教学中需要突出借助图示解决问题的策略，通过画图（如图8）帮助学生把题目信息直观化、数量关系清晰化，从而能结合分数的意义找到解决问题的方法。

经过观察、分析，学生发现每一次喝的牛奶量是上一次剩下的一半。这时教师可以提问：“你能用一幅图来表示吗？”以此引导学生进行迁移思考。学生可以用一个正方形表示一杯牛奶，用不同的颜色表示每一次喝的量，再用一个算式概括出规律（如图9）。

（2）借助数对，渗透函数思想

教师要善于从学生的生活中挖掘其积累的感性经验，激发学生学习兴趣的同时借助数形结合思想向学生渗透函数思想。

例如，“用数对确定位置”的一道习题（如图10）。

教师要结合平移知识，引导学生思考“图形平移后，表示顶点位置的数对有什么变化”。学生思考后可以发现图形平移引起数对变化的规律。通过图形变换对应数对的变化，学生建构出图形和数量间的联系，体会到数形结合的思想，也在不知不觉中接触了函数思想。

（3）结合图示，用“形”的变化体会“数”的神奇

折线统计图是数形互助的有力体现。教师要引导学生观察表格内数据的大小、感受图表上数据的变化情况，顺势而导，引出折线统计图。在学习过程中，学生经历了折线统计图的形成过程，体会到“数—形—数”的完整分析过程，从而体会到数形结合看问题的好处。

例如，“统计”的一道习题（如图11）。

面对这样一道综合题，教师可以先让学生独立完成，引导学生在描点连线的过程中感悟数据与所画折线图之间的联系，深入思考所画的折线图反映的数据增减变化情况，促进学生进行合理推理。

“数无形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。”数形结合的数学思想方法并不是多么深奥的知识。在小学的数学知识体系中，只要教师做好教学设计，学生就能自觉地运用数形结合思想去解决一些实际问题，主动用数学的眼光去认识和处理生活中的事件，感受数学的魅力，去欣赏数学那片独特的风景！

［ 参 考 文 献 ］

[1] 田丹妹. 数形结合思想方法在小学数学教学中的应用策略研究：以人教版五年级为例[D].锦州：渤海大学，2017.

[2] 王舒瑶.数形结合思想在小学数学教学中的应用研究[D].重庆：西南大学，2015.