巧用平移建联系，数形结合探性质

张艳

摘   要：从单元整体视角出发，通过唤醒学生学习y=ax2的相关内容与经验，结合解析式、表格、图象，引导学生探究y=a（x-h）2与y=ax2从数到形的区别与联系，从而自主得到形如y=a（x-h）2的二次函数图象与性质.数形结合是解决函数问题的重要数学思想 .从特殊到一般，利用平移探究函数图象是初中阶段研究函数的重要方法.

关键词：单元整体；深度学习；直观想象；代数推理；类比迁移

华罗庚曾说过“数缺形时少直观，形少数时难入微”，二次函数因其既有解析式又有图象，利用数形结合思想常常能够巧妙地解决相关问题.在新授课的教学中，就应该注重数形结合的渗透.然而由于二次函数解析式形式相比于一次函数更多样，图象性质也比一次函数更复杂，学生在解析式系数与图象的关系上更容易混淆.因此在二次函数图象和性质一节中，针对从y=ax2到y=a（x-h）2+k的探究，若能从单元整体视角设计，结合函数的平移，即可以让学生更深刻地理解不同形式的二次函数解析式之间的关系，又可以让数形结合的渗透更加水到渠成.下面将以y=a（x-h）2图象与性质一节课教学设计为例，阐释如何借助单元整体视角，抓住解析式从特殊到一般的内在关联，自然地渗透数形结合思想.

1  回顾旧知，唤醒研究方法

（1）在坐标纸上画出函数y=x2的图象，并归纳步骤.

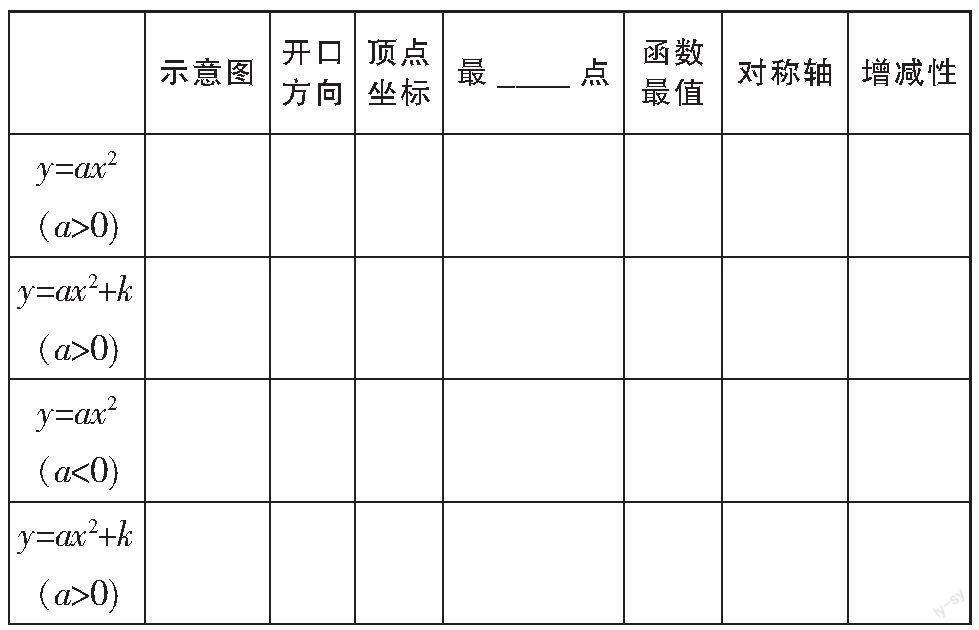
（2）以表格形式让学生回顾，如表1.

（3）问题1：从解析式和图象上思考y=ax2与y=ax2+k的联系.

问题2：k的意义？

设计意图：（1）画y=x2函数图象既能让学生回顾研究函数图象与性质的一般步骤，其表格和图象对后续新函数y=（x-1）2还起到参照作用，更直观地得出两个函数之间的联系.（2）表格的呈现，一方面让学生回忆起前两次课从哪些方面研究二次函数图象与性质，另一方面直观地感受y=ax2与y=ax2+k在填写内容上的区别与联系，从而使学生更好地回忆起后续的两个问题.（3）问题1提示学生从数和形两方面思考联系，代数方面，解析式y=ax2+k比y=ax2多了一个k，图象方面，y=ax2+k可以由y=ax2上（下）平移k個单位得到.这两方面联系均与k有关，从而引出k的意义：从数上说，他是自变量为0时的函数值，从形上看，他是函数与y轴交点的纵坐标.

2  研究方法迁移，探索表格奥秘

任务：以y=（x-1）2为例，研究形如y=a（x-h）2的函数图象与性质.

步骤1：列表

问题1：许多同学填写表2的第一行延续了表3第一行的取值，回忆表3的画图过程，这种自变量取值方式对画图有何帮助？可以得出什么结论？

问题2：猜想y=（x-1）2图象是否也会关于y轴对称？是否也具有对称性？

问题3：未画图，如何让猜想更具有说服力？

问题4：表2的自变量取值有没有更好的方式？

问题5：填好表2后，通过表格，你能初步想象出y=（x-1）2的图象形状与位置吗？

设计意图：函数表格中的每一列x，y和点坐标一一对应，因此表格中数的规律可以反映其图形特征.通过问题1，唤醒学生通过两对y值相等得出对称轴从而画出对称的函数图象这一经验，思考表2的填写方式，调整自变量的取值，使得y的值与表3相同.从而透过表格验证问题2的猜想.在动手画图之前提出问题5，旨在发展学生的直观想象能力，渗透数形结合思想.

3  画图验证猜想，直观揭示联系

步骤2：在坐标纸上描点，连线，获得函数图象.

问题1：通过5个点，我们描绘出的函数图象直观上看是关于x=1对称的，你能利用点与图象的位置关系证明这个结论吗？

问题2：将函数y=（x-1）2补充在表1最后一行下方，自行完成相关性质的填写.

问题3：结合上课初始所画y=x2的图象，思考二者联系.

问题4：你是如何发现二者联系的？

问题5：利用表格，能否佐证你的发现？

问题6：结合表格，思考如何证明y=（x-1）2可由y=x2向右平移1个单位得到？

设计意图：直观的结论需要通过严谨的推理方可成立，问题1和6对学生的要求较高，例如问题1学生需要设x=a，带入解析式得到y的值，再将A（a，（a-1）2）通过x=1对称得到新的点坐标A' （2-a，（a-1）2），最后验证A'落在y=（x-1）2上.设计问题1，可以发展学生的代数推理能力，也让学生进一步体会形的直观与数的严谨.

利用课前的知识回顾表格，能更直观地感受y=（x-1）2和之前的函数在性质上的区别与联系.问题3-5引导学生思考产生这些联系的本质原因.问题3 先从图象入手，能较为直观地得到平移的关系，再从两个表格第一行每个数值对应差1，第二行相同，这一代数角度印证5个点存在平移关系，问题6要求学生将5个点的平移关系一般化到任意点，从而推理证明结论，再次让学生经历由直观猜想到严谨论证的思维过程，培养学生思维的严谨性.

4  从特殊到一般，归纳图象性质

步骤3：以y=（x-1）2的图象性质结论，推广得出y=a（x-h）2的函数图象与性质

问题1：不画图，你能说出y=（x-2）2是如何由y=x2平移得到的吗？

问题2：解析式如何反映平移情况？

问题3：将函数y=（x-h）2补充在表1最后一行下方，自行完成相关性质的填写

问题4：y=（x-h）2与y=x2解析式是否也有相同之处？

问题5：将函数y=a（x-h）2继续补充在表1最后一行下方，完成相关性质的填写

问题6：类比y=ax2+k中k的意义，思考h的意义

设计意图：通过问题1，2让学生感受解析式中参数h和图象平移之间的关系，利用控制变量法，先让学生理解y=（x-h）2与y=x2的平移关系后，通过问题4，让学生关注到二者的二次项系数相同，再次体会参数a决定了二次函数图象的开口大小与方向，即二次函数的形状.从而自然地将y=a（x-h）2与y=ax2联系起来，得到y=a（x-h）2的图象与性质.

5  教学思考

《义务教育数学课程标准（2022年版）》中指出，课程目标的确定，立足学生核心素养发展，集中体现数学课程育人价值.而结构化、情境化、凸显学科大概念的知识，发展核心素养的功能最强.单元是知识结构化的重要表现，深度学习倡导单元学习[ 1 ].二次函数解析式形式多样，人教版《义务教育教科书数学》九年级上册“二次函数的图象和性质”中包含了y=ax2，y=ax2+k，y=a（x-h）2和y=a（x-h）2+k四部分内容，传统教学中教师往往是通过对某个具体函数进行五点法画图，观察图象特征，或通过几何画板展示若干同样形式的函数图象，由学生观察共性，从而得到函数性质.采用这样的教学设计，学生往往是以孤立的方式记忆每个形式解析式的图象性质，对于学困生而言，知识容易遗忘混淆.本节课从单元整体视角出发，抓住研究函数图象的基本步骤：列表，描点，连线，将y=（x-1）2和y=x2分别从表格、点、图象方面进行对比，从数和形感知二者的平移关系，使学生在掌握了y=ax2图象性质的基础上，仅需部分调整，就能得到y=a（x-h）2的图象性质.这种教学设计同样适用于研究y=ax2+k，即教材中探究完y=ax2后，对于y=a（x-h）2和y=ax2+k的探究是不分先后的.只不过由于y=ax2+k和y=ax2的关系与正比例和一次函数的关系类似，从认知理论来说，先研究y=ax2+k学生更好接受.在该设计下，对于y=a（x-h）2+k，学生完全有能力自己獨立探究，获得图象性质，从而建立起二次函数图象与性质的知识网络.

另外，新课标强调逻辑推理不仅仅存在于几何中，代数也应该关注推理能力的渗透.因此在观察出图象对称，以及图象间的平移关系后，尝试着要求学生通过代数推理论证.该要求一方面能够让学生完整地经历观察—猜想—论证的思维过程，强化学生思维的严谨性；另一方面示范了如何借助点坐标完成坐标系背景下相关图形猜想的证明，由数证形，渗透了数形结合思想，为解析几何打下基础.

参考文献：

［1］ 刘月霞，郭华.深度学习：走向核心素养（理论普及读本）[M].北京：教育科学出版社，2018.