2021年数学新高考Ⅰ卷解三角形综合题的特点与教学启示

黄春霜 彭永婷

摘  要：深度分析2021年数学新高考Ⅰ卷解三角形综合题（第19题）的特点，从中得到解三角形综合题教学启示.追根寻源，回归教材，建构解题思维模型；提升迁移应用能力.

关键词：解三角形；方法探源；核心素养；试题分析；教学启示

2021年数学新高考Ⅰ卷第19题是解三角形综合题，考查基本知识的迁移，将三角形的基本要素求解与证明和正余弦定理、面积、向量等内容高度融合，对学生的思维品质，信息提取与整合能力等提出较高要求.新课改所提倡的逻辑推理、数学运算等核心素养在这一题中体现得淋漓尽致.本文以新高考Ⅰ卷第19题为例，深度挖掘解三角形综合题隐含的思想方法及其在教材中的呈现内容及形式，并结合教学实践提出教学策略及建议.

1  呈现试题与解法分析

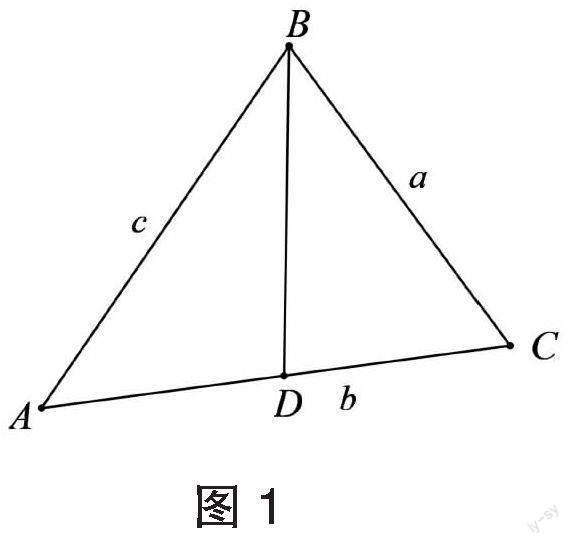
（新高考Ⅰ卷T19）如图1，记？驻ABC是内角A、B、C的对边分别为a、b、c.已知b2=ac，点D在边AC上，BDsin∠ABC=asinC.

（1）证明：BD=b；

（2）若AD=2DC，求cos∠ABC

分析： （1）应用正弦定理求解，内容略.

（2）此问可用两种解法（三角法、相量法等）解答.

解法1——采用三角法

整理得，6a2-11ac+3c2=0，方法同上.

2  研究试题特点

2.1  试题解法来源教材

该题解法1采用三角法，既可结合两相邻三角形邻角互补其余弦值互为相反数；也可用嵌套三角形中同角的余弦值相等，兩次活用余弦定理列出方程进而求解.此法源于教材， 人教版《普通高中教科书数学》必修第二册A版（2019年版）第53页第15题就是采用此法，可见该法应用的重要性.此题得到的结论也叫中线性质定理，对其结论稍作变形即为“平行四边形两对角线的平方和等于其两邻边平方和的两倍”.追根溯源后发现该结论在教材人教版《普通高中教科书数学》必修第二册A版（2019年版）P39例2以探究的形式出现，而教材中却是借助向量工具来探究的.平行四边形若只看其中一半时，发现此图类似“爪子”的形状，而“爪”图在向量一章被广泛应用，从而想到利用平面向量基本定理.自然就有了解法2向量法的产生.同时笔者发现此种解法与教材中用向量推导余弦定理，简直如出一辙.教材P42探究余弦定理的过程即是从向量运算的三角形法则出发，让向量与其自身作数量积运算，借助向量数量积、模等的运算得到了体现三角形边角关系的重要定理之余弦定理.两种方法都有效渗透了转化与化归、数形结合、方程等思想.

2.2  渗透学科核心素养，强化思维品质考查

逻辑推理是得到数学结论、构建数学体系的重要方式，是数学严谨性的基本保证，是人们在数学活动中进行交流的基本思维品质[ 1 ].学生在未来生活中能否发现问题、分析、解决问题很大程度上依赖于直观想象素养是否真实落地.2021年新高考Ⅰ卷第19题，试题要求学生对题目所给条件进行恰当逻辑推理、综合分析后，证明边长相等，并求出角的余弦值.解答过程中通过直观想象画出图形，辅助理解显得尤为重要.通过方程组思想列出方程后能否解出正确答案，考查了学生的数学运算素养.

2.3  落实课程标准，考查学科关键能力

人教A版中解三角形这一节的内容新课标明确提出：探索任意三角形边长和角度关系；掌握正、余弦定理；运用正、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题，是现阶段高中生应有的学科能力.解决2021年新课标Ⅰ卷19题涉及的必备知识是正、余弦定理，面积公式、三角恒等变换、向量等.此题并非常规地利用正、余弦定理或者面积公式来求解三角形，而是通过两次应用余弦定理建立方程组进行相关的推理运算.在课标要求的基础上对试题进行了重新归整，着重考查学生的学科逻辑推理能力，以及运用数学思想方法解决问题的能力.

2.4  稳中有变求创新，考查类比迁移和综合应用能力

直面高考的热点与难点，是全国卷高考题一大特点.例如，近三年全国卷中都有涉及解三角形知识的考查，但考查的方式不尽相同[ 2 ] .2019年全国文、理数学卷都以解答题方式考查解三角形，涉及正余弦定理、三角恒等变换等知识内容的运用；2020年江苏卷考查对嵌套三角形的求解，与今年考查题型类似；全国Ⅱ卷17题考查解三角形求角、求周长最值问题；2021年考查解三角形时，注重通过落实基础知识提高学生运算能力.往年更多的是三角求解，今年是三角证明，不过道理相通.不难发现，这几年对解三角形知识内容的考查，试题难度基本保持稳定，考查内容涵盖了三角函数内容的所有知识点，对学生的综合应用能力也是提出了较高要求.

3  教学启示

3.1  追根寻源回归教材，建构解题思维模型

在教学中通过挖掘教材中例题、习题、定理、公理所隐含的数学思想方法，使学生了解到高考中所用的一些解题思想方法并非无源之水，无本之木，而是源于教材、高于教材，从而使学生更易理解和掌握[ 3 ].通过对教材的典型例题、习题进行恰当梳理和必要拓展，分门别类构建解题的思维模型，是提升学生学习效率的重要途径之一.例如，本题中探究的“爪”型图对学生来说并不陌生，学生在人教A版必修二（2019版）第六章的学习中从向量的线性运算，平面向量基本定理的学习，再到平面向量的应用中，一直在接触类似模型处理问题.在平时教学中可对此图可能涉及的多种情况进行规整，包括中线定理，角平分线定理，三等分点或者更为一般的位置.利用它们的探究结论引导学生推导比较，发现其一般规律，以后学生再遇到此类问题时即可迅速分辨其所属类型，提取已有的相应思维模式迅速答题.

3.2  加强模块专题化复习，提升迁移应用能力

梳理近年高考三角综合题的高频考点，构成常考专题知识体系，加强专题化复习和重难点突破.解三角重点突破如下项目：正余弦定理直接应用；三角函数取值范围问题；周长、面积取值范围问题；嵌套三角形求解问题等.专题复习时，应根据学生本身实际情况设定相应专题训练的例题和习题，并提升学生迁移应用能力.以学习人教A版必修二第六章——余弦定理为例，学生需要熟悉如集合、函数、三角函数、向量等基础知识.这些基础知识都将有助于直接破解余弦定理发现和证明等难题.在探究余弦定理的过程中，教师创设的问题呈现形式也应尽可能有利于学生知识迁移能力的培养.例如，可以问学生，你能否用代数式形式表示出它的边角关系？对于此问题，学生给出的结论可能多种多样，教师在一一分析解答中，学生知识迁移和应用能力都将得到提升.

3.3  依托真实情境和跨学科融合，强化探究的过程体验

真实情境是培养学生知识探究能力的重要依托.应当深入挖掘在真实情境中隐含的教学内容，以及它们所涉及的数学本质、规律和思想方法等.例如，人教A版必修二第六章所学的向量相关知识是有很强的物理学科韵味的.从物理中位移、力的合成得到启发，引进向量的加法；由力和位移两个向量，明确做功这一标量，受到启发，引入向量的数量积；研究小船行程最短或时间最短问题时，学生是有一定生活经验的，让他们想象自己在河中游泳，如何到达？问题设计时可以只有题干，没有问题，由学生自己提出问题并解决问题.倘若教学中教师能精心选择跨学科素材，以自主学习或合作探究模式进行解法探索和过程体验，就能让学生的深度学习真正发生.

3.4  强化学科思想方法渗透，提升学科核心素养

以中国高考评价体系为指导思想，落实立德树人任务，是新高考背景下学科教学的时代使命.依托数学知识，淡化特殊技巧，探究数学本质，培养数学核心素养，是提升学生发现、分析、解决问题能力的必由之路.教师唯有通过在教学中把握学生的认知规律，教会学生如何追本朔源，弄清问题本质，学生才能举一反三，融会贯通，才有可能真正领悟数学思想的真谛.例如，因三角形隶属于几何图形，从平面几何的角度出发探究问题本质，是数形结合思想重要体现.从实际问题构建数学模型，将现實生活中测量角度、高度、距离等问题转化为可解的三角形问题，让数学真正回归生活，也是数学的本质所在.结构不良开放试题也是近几年新出现的题目类型，在解三角中经常被采用.教师在教学时可通过此类题型，对教学内容进行优化重组，与学生在问题的探究过程中，让知识脉络更加清晰.同时，学生的逻辑推理、直观想象、数学建模、数学运算等核心素养也能得到提升[ 3 ].

总之，对照课程标准，深研教材原型，建构思维模型，加强模块整合，强调跨学科融合，渗透数学思想等教学举措能有效增强学生学习“解三角形综合题”效果，促进学科核心素养在高中数学课堂教学的生根发芽.

参考文献：

［1］ 李作滨.素养导向的数学测评研究：以2018年高考为例[J].数学教育学报，2018，27（6）：33-37.

［2］ 杨孝斌，周国利，周娅.两道“解三角形”高考题的解法研究、比较分析及教学启示：以全国Ⅲ卷理科数学2017年第17题、2019年第18题为例[J].兴义民族师范学院学报，2020（1）：112-116，124.

［3］ 林运来.基于逻辑推理素养的高三复习教学[J].中学数学，2018（9）：24-26.