数学抽象素养在中学数学教学中的应用分析

王德朋

摘   要：为贯彻落实“立德树人”根本任务，在中学数学教学中，要以培养学生学科核心素养为导向.数学抽象素养在六大核心素养中是最为基础也是极为关键的核心素养，并能够为另外五大核心素养的培养进行铺垫.在解决数学问题时，数学抽象思想方法是必不可少的.文章主要从基本概念、数学抽象的基本形式、数学抽象的应用案例及结论四部分介绍了数学抽象在中学数学教学中的应用.

关键词：中学数学教学；数学抽象素养；应用

自2017年高中数学课程标准修订以来，教学教育坚持以“立德树人”为根本任务，并相应地提出了六大数学学科核心素养.在高中数学教学过程中要以培养学生相应的核心素养为导向，并贯穿于教学的全过程中.数学抽象作为最基础的核心素养，在高中数学中都有所体现.教师在数学教学过程中通过知识的讲解与应用，即从实际的生活问题中抽象出数学问题进行解决，来逐步培养学生的数学抽象素养.

1  基本概念

1.1  抽象的概念

抽象是指在大部分事物中提取出共同本质特征，放弃其中非本质特征的思维过程[ 1 ].抽象要通过对比选择出最根本的特征.在生活实践中，抽象是运用判断及推理等形式去粗求精的过程.

1.2  数学抽象的概念及表现

数学抽象是在实际问题中把数量与空间形式进行抽象，以此形成相关研究对象的素养.数学抽象是数学教学中最基本的思想，把数量与数量之间、图形与图形之间的关系抽象成概念与概念之间的关系，从具体事物中抽象出共同特点，一般结构，赋予数学语言来表达[ 2 ].其主要表现是：通过抽象，得到概念以及规则，提出模型，构成数学思想方法，并建立数学体系.教师在中学数学教学中要引导学生在情境问题中抽象出数学的概念、方法与体系，养成从具体情境抽象出数学问题的习惯，学会运用抽象思维去解决实际问题.如图1所示.

2  数学抽象的基本形式

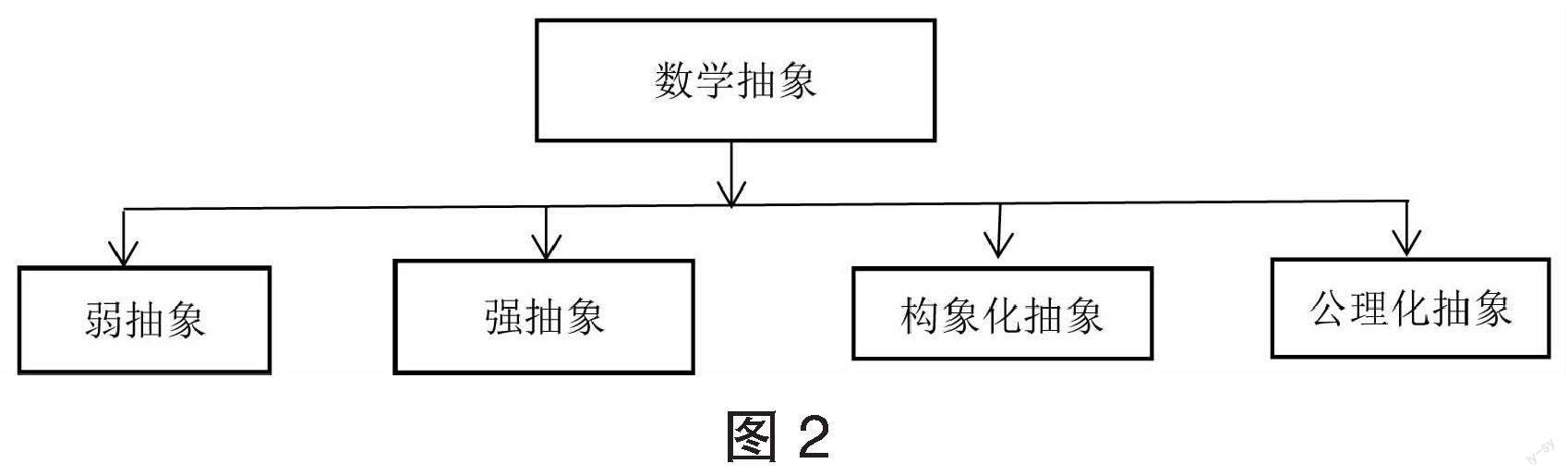
如图2所示，数学抽象的基本形式有弱抽象、强抽象、构象化抽象及公理化抽象，下面对于这四种基本思维形式作以介绍.

2.1  弱抽象

弱抽象是对某一事物的一个特征或从该事物的侧面进行抽象，形成比原事物更一般的理论和概念.通过抽象，形成了一个鲜明的特例，保留抽象出来的本质，原事物其他性质将被忽视.这个抽象也被称为“概念扩展性抽象”.例如：在各种各样的物体的计数上，要抽象出整数的概念，原物体的性质就会视而不见了，只考虑数的概念来确定整数的概念.

2.2  强抽象

强抽象是在原有事物的基础上賦予一些新的特征，从而形成新的概念的过程.这个新概念就会是原事物的一个特例，也被称为“概念增加性抽象”.例如：在一个平行四边形的概念基础上，给其赋予一个新的概念“两组对边平行且相等”，就会形成一个新的矩形的概念.

2.3  构象化抽象

构象化抽象是在原事物基础上不能直接进行抽取，而要将数学对象理想化对待，赋予其构思想象的过程.此抽象的作用是在原事物的基础上增添一种新的元素，使得其数学结构更加完备，因此，又被称为“新元素添加完备式抽象”例如：在有理数的基础上，构想出了无理数，就构成了实数，使得其系统更加完备.

2.4  公理化抽象

公理化抽象是在原有的基础上，为了数学的发展，通过构思想象出了新的概念法则，并让新法则更理想，符合要求，使得数学理论体系更加完善.此法则也叫“公理更新完善化法则”.例如：“非欧几何学平行公理”就是通过公理化抽象而得来的.

3  数学抽象在中学数学教学中的应用案例

3.1  哥尼斯堡“七桥”问题

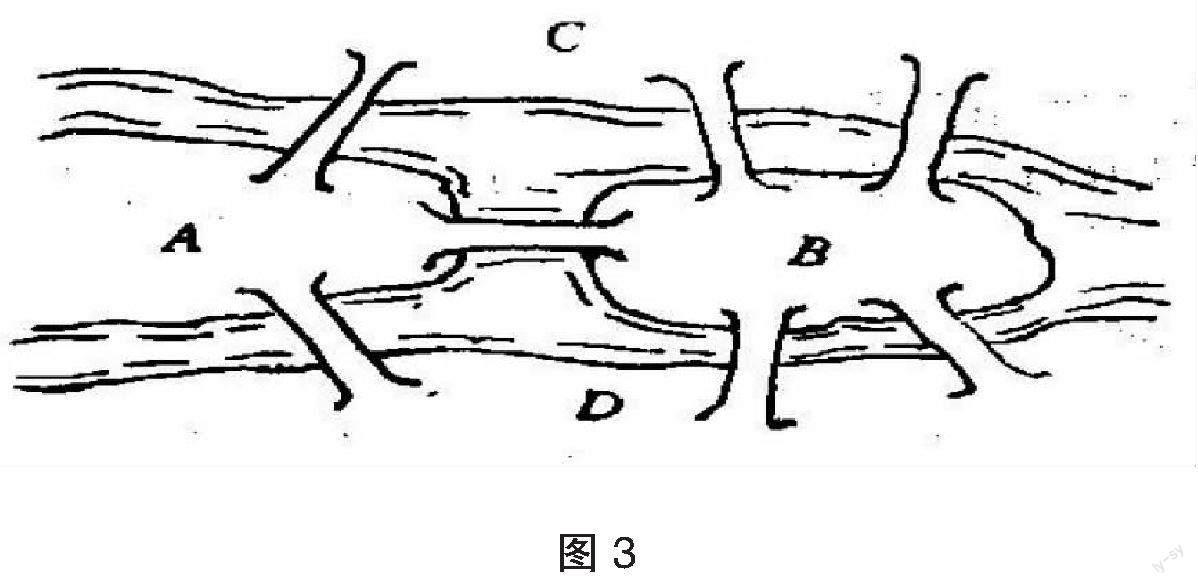
一条大河横贯哥尼斯堡城区，共有两个支流.市区内有七座大桥，其中五座与河中的小岛相连.该岛风景优美，市区的居民们在闲暇时间都喜欢来岛上游玩，瞻仰康德的雕像以及游玩.时间一长，就有居民对七座大桥产生了兴趣，并尝试着能否一次性通过七座大桥，且不能在每一座桥上重复通过[ 3 ].这就是哥尼斯堡“七桥”问题的由来.如图3所示：

人们对各种方案进行尝试，都达不到一次性通过七座桥的效果.著名数学家欧拉转换思路，运用抽象的方法用七条线段代替七座桥，用四个点代替四块陆地，如图4所示.这样就会产生一个新的问题，“怎样一笔将七条线段一次性连接起来，且只有一个起点和终点？”即“一笔画”.欧拉经过分析，得到了一个结论：一笔能够画完的图，“奇次点”要么没有，要么有2个.但图4却有4个，即不能一笔画完，于是得出不能一次性通过七座桥的结论.

通过这个例子，可以深刻体会到运用抽象的思维来解决实际问题的巨大优势.在中学数学教学中，教师在介绍用抽象思维解决问题时，可以运用这个案例让学生体会数学抽象的重要性，培养学生的数学抽象素养.

3.2  数学抽象在“函数”中的体现

“函数”内容在中学数学中是十分重要的一块内容.该内容的学习有利于实际问题的解决.首先如何理解“函数符号y=f（x）”的意思呢？y=f（x）是一个数学符号，用来表示“y关于x的一个函数”而不是f与x相乘.例：y=2x+1也能够写成f（x）=2x+1，如果将x=3带入其中会得到y=7，也可以写成f（3）=7.通过对函数符号的理解，可以使学生进一步体会到抽象的思维方法.对于一些数学符号的理解与运用，能更好的培养学生的数学抽象素养.此外，在函数的一些性质里，也体现出了数学抽象的运用，如函数的单调性，奇偶性等等.当用数学语言表示函数的单调性时，借函数y=x2的图象展示.设函数的定义域为J，且区间D包含于J，在D上任意取两个值x1和x2，且x1＜x2，都有f（x1）＜f（x2），则函数f（x）在区间D上是增函数，即“单调递增”，如图5所示.同理，若都有f（x1）＞f（x2），则函数f（x）在区间D上就是减函数，即“单调递减”，如图6所示.

函数的奇偶性在对于定义的理解上以及用数学语言表示奇偶性都体现了数学抽象的应用.“奇函数”是对于函数定义域内任意一个x都存在f（-x）=-f（x），图像关于原点对称.“偶函数”是对于函数定义域内任意一个x都存在f（x）=f（-x），图像关于y轴对称.

对于三角函数的教学，数学抽象的运用更是必不可少的.例如，对任意角三角函数定义的理解；能根据三角函数的定义推导同角三角函数的基本关系式并且掌握；利用单位圆能够找到不同角的关系并理解诱导公式；利用三角恒等变换的公式解决一些问题；此外，在三角函数的应用上，将一些实际问题转化为三角函数问题来解决.通过对于函数的定义理解以及赋予数学语言，及在实际问题中的应用，教师在教学上能够更好地培养学生的数学抽象素养，锻炼抽象思维.

3.3  数学抽象在“数列”中的体现

“数列”这一章是选择性必修部分的内容，也是高考中最重要的一部分内容之一.尤其是等差数列及等比数列相关的知识及其应用，是学生必须要掌握的内容.培养数学抽象素养在其中也是教学目标的重要内容.

（1）等差數列

从生活实例中，能够抽象出等差数列的概念，以及对于通项公式能够有深入的理解.例如：

{1}某人贷款买车，每月需要等额分期还款，每月还款钱数（元）分别是：2000，2000，2000，2000，……

{2}小学生数数，从1到100，即1，2，3，4，……

通过观察这些数据有什么特点呢？以上两组数据都是从第二项起与前一项之差为同一个常数.那么，就可以从以上两个生活实例中抽象出等差数列的概念，即“一个数列从第二项起，每一项与前一项的差都是同一个常数，这个数列即是等差数列[ 4 ].”同时，赋予数学语言，首项为a1，公差为d，得到通项公式an=a1+（n-1）d.理解等差数列通项公式与一元一次函数的关系也能够培养学生的数学抽象素养.

（2）等比数列

对于等比数列的概念，通过实例也能够有所体现.例如：

{1}某动物细胞细胞分裂，分裂的个数会由1个变成2个，2个变成4个，4个变成8个，以此类推，即1，2，4，8，……

通过观察以上2个案例，就能观察到从第二项起与前一项之比为同一个常数.能够从中抽象出等比数列的概念，即“一个数列从第二项起，每一项与前一项的比都是同一个不为零的常数，这个数列即是等比数列[ 4 ].”用数学符号表示为：首项是a1，公比是q（q≠0），通项公式为：an=a1·qn-1.同时，对于等比数列与指数函数的关系也能体现出数学抽象思想.

4  结论

本文对抽象与数学抽象的概念及四种基本形式做了相关介绍，并通过哥尼斯堡“七桥”问题、函数及数列的相关内容来体现数学抽象思维方法.数学抽象是数学教学中最基本的思想，在解决一些实际问题时，数学抽象思维是至关重要的.在授课过程中要引入一些生活实例，将实际问题转换为数学问题来加以解决，锻炼学生的抽象思维.在新课标的引导下，为把学生培养成全面发展的人，应基于学生原有素养，提升学生抽象思维能力，培养学生数学学科核心素养.高中数学的各部分内容都能够培养学生的核心素养.教师在教学过程中，不仅仅要讲授数学知识，更重要的是通过在课堂上与学生进行互动交流，使学生能够积极的参与到课堂中，达到培养学生数学学科核心素养的效果，从而使学生的整体素质得到提高.

参考文献：

［1］ 张胜利，孔凡哲.数学抽象在数学教学中的应用[J].教育探索，2012（1）：68-69.

［2］ 中华人民共和国教育部．普通高中数学课程标准（2017 年版）[M]．北京：人民教育出版社，2018：4-5．

［3］ 郑泉水.哥尼斯堡七桥问题的启示[J].中学生数学，2018（24）：17-18.

［4］ 李龙才，周远方.普通高中教科书教师教学用书.数学选择性必修二A版[M].北京：人民教育出版社，2019.