基于数学核心素养评价框架的新高考试卷分析——以2020—2023年全国数学新高考Ⅰ卷为例

王静逸, 张曜光, 杨光伟

(1.浙江师范大学教师教育学院,浙江 金华 321004;2.金华市教育局教研室,浙江 金华 321017)

为了落实“立德树人”的根本任务,《关于全面深化课程改革,落实立德树人根本任务的意见》中详细说明了高考改革的具体方向,高度强调了学生核心素养的培养,不再进行文理分科,以促进学生全面发展.同时,我国高考评价体系提出并说明了“一核四层四翼”的要求,注重核心素养导向的学生数学发展[1].

根据教育部印发的《新高考过渡时期数学学科考试范围说明》,2020年起全国部分省市开始实行新高考卷,这是新课改颁布以来第一次启动文理不分科的新高考试卷.高考试卷是对高考改革最直接的反映,对新高考试卷中核心素养考查情况的研究可以为新高考改革的情况提供实证依据.由此,笔者根据《普通高中数学课程标准(2017年版)》(以下统称《课标》)中对数学核心素养的划分,结合喻平提出的核心素养的3个水平,对2020—2023年全国数学新高考Ⅰ卷(以下统称新高考Ⅰ卷)试题进行分析,以期探求新高考背景下数学核心素养的考查情况.

1 研究方法

1.1 研究框架的建立

《课标》中提出了六大核心素养的3个水平,但喻平对其实际可操作性以及合理性提出了疑问,提出了以知识为载体进行评价的新核心素养水平考查模型,即以3种不同的知识学习形态(知识理解、知识迁移、知识创新)来划分每个核心素养下关键能力的3种水平[2].而后,李华等人根据喻平所提出的核心素养评价框架和《课标》中对六大核心素养内涵的描述确立了18个层次的评价标准.文章以此评价标准为研究框架,对2020—2023年新高考Ⅰ卷进行赋值和分析.

1.2 数学核心素养指标量化赋值

为更明确数学高考试卷的核心素养考查情况,要对核心素养水平如何进行评价有深入的理解.首先,高考试题中六大核心素养交汇融合、相互关联,呈现出综合考查的特点,因此一道题中可能会出现对多种核心素养的考查,且水平不一.其次,高考试题的解法各不相同,不同的解法会影响对试题核心素养考查情况的分析,因此本文仅选择参考答案中的解法来进行赋值.再次,各试题分值不一,因此各试题中各核心素养的不同水平的赋值也不同.

基于对研究框架的理解,笔者参考李华、胡典顺对2019年高考数学全国卷的核心素养考查水平的赋值模式[3],将字母A,L,M,I,O,D分别对应考查到的六大核心素养:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析,而字母的下标1,2,3分别表示考查的核心素养水平属于知识理解水平、知识迁移水平和知识创新水平.下面笔者以两道试题为例进行具体的赋值说明.

例1已知正方体ABCD-A1B1C1D1,则

( )

A.直线BC1与DA1所成的角为90°

B.直线BC1与平面BB1D1所成的角为45°

C.直线BC1与CA1所成的角为90°

D.直线BC1与平面ABCD所成的角为45°

(2022年全国数学新高考Ⅰ卷第9题)

赋值说明此题主要考查学生运用已学立体几何的相关知识,在熟悉情境之下,对线线、线面位置关系进行推理判断,属于知识理解层面的题目.此题满分为5分,主要考查学生逻辑推理素养和直观想象素养,因此,标定相应的指标分数值为L1-2.5,I1-2.5,表示在知识理解水平下的逻辑推理素养和直观想象素养,分别赋值为2.5分、2.5分.

例2过点(0,-2)与圆x2+y2-4x-1=0相切的两条直线的夹角为α,则sinα的值为

( )

(2023年全国数学新高考Ⅰ卷第6题)

赋值说明该题是一道分值为5分的单选题,主要考查直线与圆和三角函数相关的知识点,属于知识理解层面的题目.例2以圆的标准方程为考查切入点,需要学生绘出圆的图像,并通过数形结合进行数学运算得到答案.因此,标定相应的指标分数值为I1-2.5,O1-2.5,其中I1-2.5表示在知识理解水平下的直观想象素养,赋值为2.5分;O1-2.5表示在知识理解水平下的数学运算素养,赋值为2.5分.

2 研究结果

2.1 新高考Ⅰ卷的结构与内容分析

新高考Ⅰ卷的试题结构为8道单选题共40分,4道多选题共20分,4道填空题共20分,6道解答题共70分(1道10分和5道12分),总分150分.增设了多选题,取消了2选1形式的解答题,这对学生的数学思维能力提出了更高的要求.多选题既能考查学生的数学“双基”能力和对核心概念的理解,又非常注重进一步考查数学思维方法[4],这充分展现了高考对学生思维水平考查的层次性.另外,在题目设置中,还出现了适度开放的题目,如2020年新高考Ⅰ卷第17题,试题的创新和改变,让学生改变以往死记硬背、靠刷题来获取高分的固态想法,转而侧重于自身的独立思考能力和核心素养能力的发展.总体而言,2020—2023年新高考Ⅰ卷的题型设置和分值排布契合高考评价体系所设定的“一核”目标,即立德树人、服务选才和指导教学的功能.

根据《课标》对高中数学内容的分类,将试题涉及的内容划分成4类(预备知识、函数、几何与代数、概率与统计).2020—2023年新高考Ⅰ卷各部分内容分值的分布中,函数、几何与代数的考查分值最多,总和均占整张卷子的75%以上;而概率与统计的分布较少,只占了15%左右;预备知识的分布最少,整张卷子中只设置了1～2道题.将2020—2023年新高考Ⅰ卷各部分分值对比,发现近4年来趋于稳定.由此可见,新高考Ⅰ卷总体侧重对函数、几何与代数的知识点的考查,而对统计与概率的考查较少,与往年的趋势保持一致,新高考改革下数学命题具有稳定性.2020—2023年新高考Ⅰ卷各部分内容分值分布如图1所示.

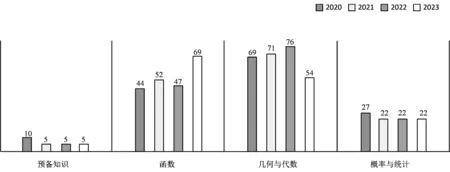
图1

2.2 数学核心素养整体考查分析

对2020—2023年新高考Ⅰ卷所有试题进行赋值,并进行整理,然后将4套试卷中各核心素养3个水平的分值转化为占整张试卷总分的权重(如表1所示).以逻辑推理素养为例,L1的权重计算结果即为逻辑推理素养在知识理解水平上的考查分值总和除以整张试卷总分.

整理发现,整体上2020—2023年新高考Ⅰ卷均较全面地考查了六大核心素养,但有所侧重.其中,数学运算素养、逻辑推理素养和直观想象素养考查最多,分别占45.8%,24%,17.6%,这表明新高考Ⅰ卷延续了旧高考数学试卷考查的重点,仍重视学生的运算能力、推理能力和空间想象能力的发展,这是学生数学思维发展的重要基础.数据分析素养考查较少,占比5.5%,数据分析素养主要是对概率与统计知识点的考查,每年对此模块的考查都较少,但趋于稳定.而数学抽象素养和数学建模素养考查最少,仅占3.8%和3.3%,二者要求学生用数学的眼光去观察、思考和表达现实世界,发现蕴藏在题目文字表述之下的数学关系,对学生数学理性思维的要求较高.如2023年第10题,结合噪音污染的实际背景,考查学生对对数函数的理解;2022年第4题,以南水北调工程为现实背景,考查棱台体积公式知识点;2021年第16题,把数学融入民间剪纸艺术,考查数列知识和化归思想;2020年第6题,结合“新冠”疫情考查学生运用数学模型解决现实生活问题的能力.此类创新情境和生活实践情境试题可以更好地体现对学科素养和关键能力的考查[5],同时体现了高考评价体系中要求的应用性和创新性.

另外,对比六大核心素养的3个水平权重均值(如图2),整体上新高考Ⅰ卷倾向于考查知识理解水平和知识迁移水平,而对知识创新水平的考查较少.这表明数学基础知识和基本思想方法的综合考查仍是高考的重点,体现了高考评价体系中要求的基础性和综合性.然而,尽管知识创新水平的考查比例较少,但对试题进行具体分析发现,知识创新水平下核心素养的考查能深入地反映学生深层次的数学思维能力,难度较大,层次明显,因此比例较低具有合理性.

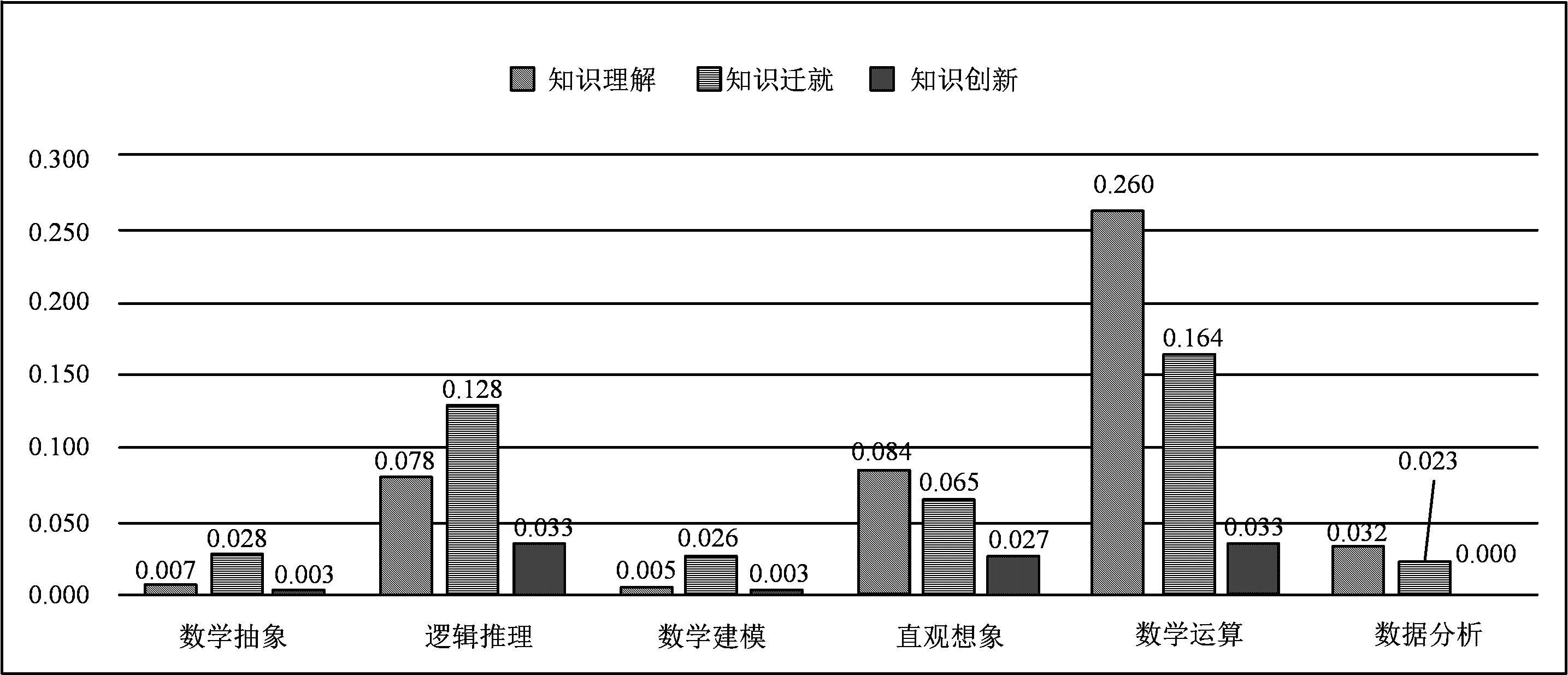
图2

2020—2023年新高考Ⅰ卷数学六大核心素养3个水平权重均值分布如图2所示:

2.3 数学核心素养水平逐年对比分析

横向对比2020—2023年新高考Ⅰ卷六大核心素养3个水平的考查情况,发现4年内六大核心素养在3个水平上的分布较为稳定(见表2):在数学运算素养上,侧重于水平1和水平2的考查,且水平1的考查均占整张试卷的25%左右,基础运算能力要求学生对运算对象、运算法则、运算意义等有清晰的认知,这是顺利解题的必备条件;在逻辑推理素养上,4年来对水平2的考查逐年增加,由2020年的6.33%提升到了2023年的18.33%,这说明新高考Ⅰ卷对学生逻辑思维能力的要求逐年提高,在解题过程中要求学生具备分类讨论、数形结合等数学思维能力;在数学抽象素养和数学建模素养上,主要是对水平2的考查,融入数学文化的情境,要求学生运用数学思维发现、分析和解决新情境中的数学问题,体现了新高考越来越重视学生理性思维的培养;而对于直观想象素养和数据分析素养,也倾向于对水平1和水平2的考查.另外,横向对比2020—2023年对水平1、水平2和水平3的考查总体权重比例,发现对水平3的考查逐年降低,分析原因,发现相较于2020年,后几年的新高考Ⅰ卷试题中融入的真实情境和数学文化元素减少了许多.

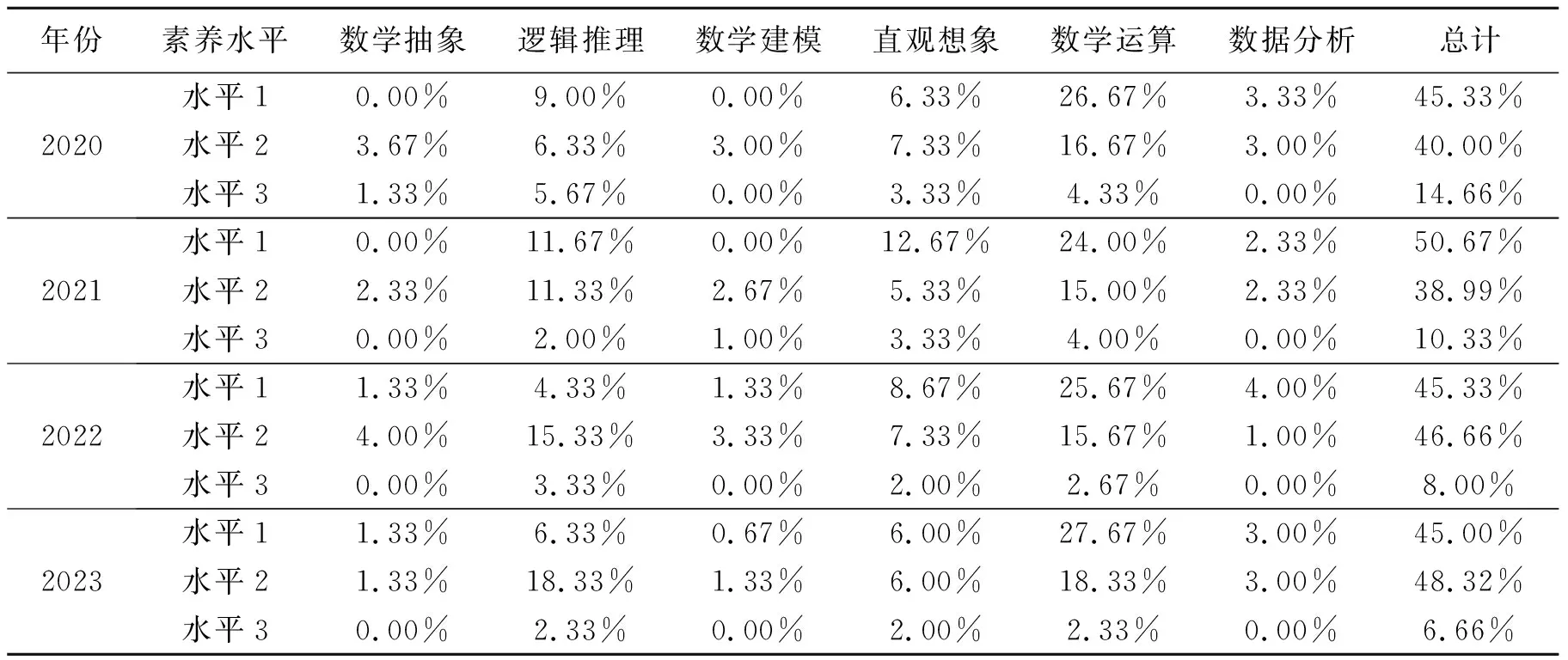
表2 2020—2023年新高考Ⅰ卷数学六大核心素养3个水平权重分布

3 总结与建议

3.1 研究结论

新高考Ⅰ卷进行了试题结构的优化,注重开放性和创新性,设置了多选题和结构不良试题,给予学生更多的思考空间,让不同层次的学生发挥他们的能力,能够起到科学选拔人才的作用.并且在内容设置上,维持以函数、几何与代数这两个内容为重,具有稳定性.

新高考Ⅰ卷对数学核心素养的考查较为全面,主要侧重于对数学运算素养、逻辑推理素养和直观想象素养的考查,平均权重分别为45.8%,24%,17.6%;并且,对六大核心素养的考查主要侧重于知识理解水平和知识迁移水平,而知识创新水平考查虽然较少,但能考查出学生是否具备理性思维;2020—2023年六大核心素养在3个水平上的考查分布较为稳定,逐年来更重视学生的基础运算能力、综合运算能力和高阶逻辑推理能力的发展.

基于以上研究分析,笔者对高中数学教学提出以下建议.

3.2 教学建议

1)重视基础,发展思维.

基础性知识即必备知识是能力发展的支柱,离开了基础知识、基本技能和基本数学思想方法,素养立意就不可能成立,因此教师在日常的教学活动中,要重视学生是否理解了基本概念、定理、性质和法则,以数学课堂与数学活动配合发展学生的“四基”,使学生知晓知识内部的关联和脉络.同时,要注重学生逻辑思维与辩证思维的发展,使学生能够逐渐养成自学的能力.

2)素养导向,能力为重.

新高考Ⅰ卷试题结构、内容不断创新,加设了多选题、开放题,融入试题背景于新的数学情境并给出新的数学定义,要求学生具有理性思维、数学阅读理解能力和更高水平的综合素质能力.在素养导向下,数学命题贯彻综合性、应用性、创新性的要求,因此在教学上教师要注重培养学生运用数学去发现和解决日常生活中问题的能力,培养学生联系不同数学知识和不同学科知识去思考的能力,还要培养学生勇于发散思维和敢于创新的态度.

3)注重德育,全面发展.

新高考Ⅰ卷贯彻立德树人的教育总目标,渗透数学文化,如将南水北调的水利工程背景、民间剪纸艺术融入试题,培养学生的爱国情怀和民族亲切感;在新冠疫情影响全球的背景下,融入病毒感染病例和时间的模型,培养学生利用数学的眼光去观察、思考、表达现实生活的态度.因此,教师要注重学生的数学德育发展,注重培养学生的情感态度价值观,将文化、人文、科学等因素融入日常教学活动中,在德、智、体、美、劳五育上进行铺垫.