放缩构造巧拟合 数形互助见本质
——例谈放缩法在函数拟合中的应用
2023-09-26孙杭哲孙波英
孙杭哲, 孙波英
(慈溪中学,浙江 慈溪 315300)
在2023年3月的宁波十校联考和4月的宁波二模考试中,都出现了零点大小关系的相关问题.宁波十校联考中的压轴题以极其“诡异”的形式难倒了一众学生,又以简约、质朴无华的解法惊艳了所有人.惊叹、赞赏之余,笔者仔细揣摩,似乎洞察出此题的核心,拟从不同视角对这一试题进行多元分析,以此猜想参考答案的由来以及函数拟合与不等式放缩的内在联系,彰显数学思想在解题中的引领作用,并谈谈笔者对于今后导数复习备考的一点看法与建议.
例1已知函数f(x)=|x-1|ex和g(x)=a|x|的图象共有3个不同的交点,并且它们的横坐标从左到右依次记为x1,x2,x3.
1)求实数a的取值范围;
2)求证:2x3-x2+x1<2a.
(2023年浙江省宁波市十校联考数学试题第22题)
1 解题预备
例1和后文的例2解题中要用到的经典放缩式如下(可作为二级结论):
1)ex≥x+1.
2)ex≥ex.
本文仅对例1第2)小题重点分析,为便于后文的分析,先对第1)小题进行解答.
1)解显然,xi≠0,其中i=1,2,3,则

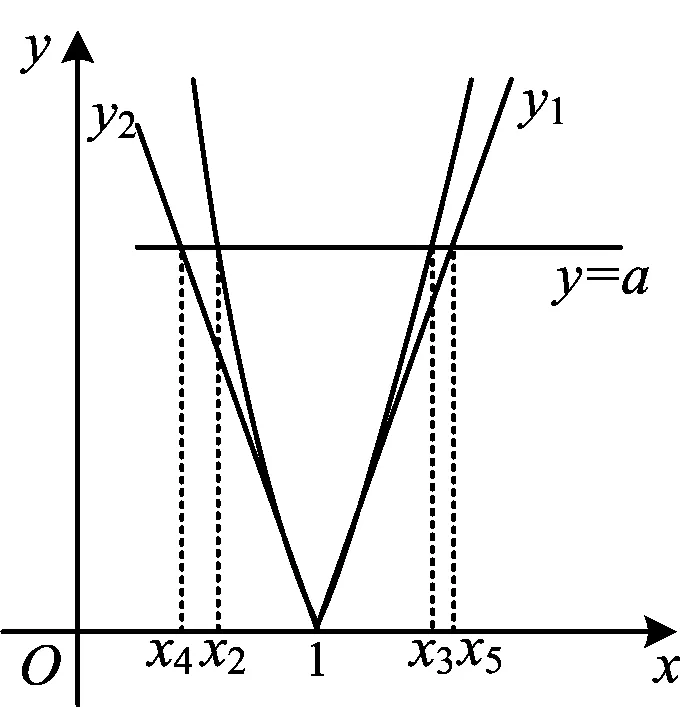
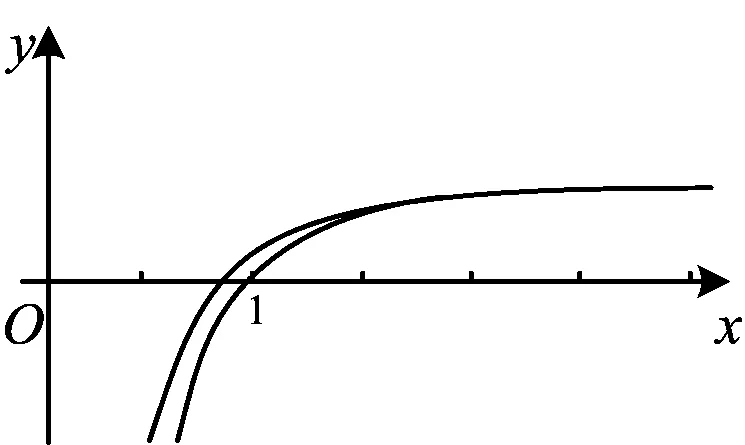
根据趋势分析可得函数h(x)的图象如图1所示,故a>0,且x1<0 图1 以下重点对第2)小题进行分析: 待证不等式虽为三元,但变量间彼此关联.比较自然的想法是对其进行拆分,化归为熟悉的类型.拆分的方式分为两种:1)x1+x2+2(x3-x2)<2a;2)(x3-x2)+x1+x3<2a.利用对称构造法不难得到x1+x2<0,证明的重点在于x3-x2 思路1结合函数图象,该函数为下凸函数,在其外侧必定存在两条切线可以把它“包住”,并且由此得到的两个零点很容易解出,以此为桥梁即可得证. 图2 该切线放缩的本质即ex≥ex. 由此可见,切线放缩只不过是线性拟合的一种,在一定程度上会将不等式变紧,但能得到降低证明难度的效果.解题时可根据需要选择特定的直线,而不应局限于“切线”.值得注意的是,割线拟合也是一种线性拟合手段. 思路2思路1利用ex≥ex进行放缩,然而ex≥x+1更为常见,能否仿照思路1求解呢? 则 函数的大致图象如图3所示,故|x2-x3|<|x4-x5|=a. 图3 这就是参考答案给出的解法: 从而 2x3-x2+x1<2a. 对上述解法进行优化,即得解法3: 即 两式相加,得 x1+x3 同理可得 两式相加,得 x3-x2 从而 2x3-x2+x1<2a. 事实上,解法2和解法3殊途同归. 探究问题往往比得到答案更有价值.答案的作用是在苦苦思索与探究无果之后,提供一种可能的思路.但答案的负面作用也很明显——它会大大限制你的思维.因此,从答案中汲取经验,为今后的解题服务,这才是答案的价值. 此题的参考答案从一定程度上解释了可利用“函数拟合”方法解题的原因.无论是零点差还是零点和、零点积,其实都是在研究函数零点之间的大小关系.如果零点可以解出,那么就转化为不等式进行求证.但大多数情况下,由于ex,lnx等元素的存在,方程往往是超越方程,不可解.可以尝试使用其他函数来逼近它,由此得到零点的大小关系.这在几何上是函数拟合(函数逼近);在代数上,是解不等式、解方程. 泰勒拟合是函数拟合的一种常用方法,即利用待定系数法在极值点处用二次函数、对勾函数拟合.但此方法有时精度不够,局限性较强.例1提供了另一种对学生而言切实可行的操作方案——利用熟知不等式进行放缩、拟合.下面再通过例2对此方法进行深入分析. (2023年浙江省宁波市高三数学第二次模拟试题第22题) 图4 lnm1+lnm2>1+ln(2a). 因为 lnx-ax2=0, 即 lnx2-2ax2=0, 所以 lnm-m-ln 2a=0, 于是只需证m1+m2>1-ln(2a).考虑使用 代入拟合即可(下略). 评注上述两种解法都用到了同一个不等式,参考答案中使用的对数均值不等式其实也来源于此.只要找到命题时的“母函数”,各种方法都可以信手拈来. 本文从例1的自然解法入手,从切线拟合到双曲拟合,从特殊的切线到一般的放缩式,并由此拓展介绍了函数拟合在解决零点大小相关问题时的多角度应用. 零点和、差、积、商问题中必定存在等式,其实质是利用等式证明不等式,“放缩式”沟通了“等”与“不等”,在超越式与有理式之间架起了桥梁.导数的本质在于“于细微处化曲为直”,函数拟合思想的重要性可见一斑.同时,换元思想对于简化问题起着重要作用,通过换元法构建新的不等式是一种常用方法.解题时可根据需要对函数进行平移、伸缩变换. 在新高考的背景下,回归本质成为复习备考的重中之重.在教材中,对于函数逼近留下了不少可圈可点的试题.在教学中,教师应利用已有习题、深挖内涵,向学生灌输这一思想.作为学生,养成画图意识十分重要.数缺形时少直观,形少数时难入微,一个个的放缩式并不是孤立的代数式,而是有其深刻的几何内涵.如果将二者割裂,那么无疑是囫囵吞枣,不得要领. 本文旨在揭示一类零点范围问题的本质,并提供一种命题的思路.但函数拟合对于高等数学知识有限的高中生而言并非是一种通法.命题手段是唯一的,但解题方法是多元的,目光不应禁锢于此.
2 解法分析
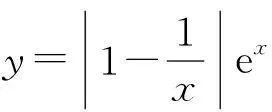




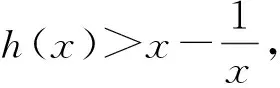

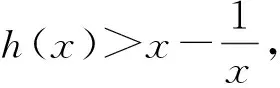
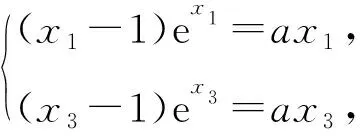
3 拓展延伸
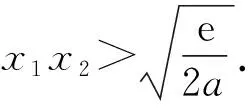
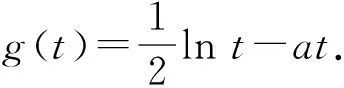
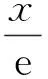

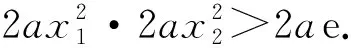
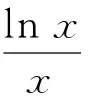
3 总结
