逻辑推理是打开数学解题之门的钥匙
——以一道模拟考试题的讲评为例
2023-09-26李金蛟
李金蛟
(常州市第一中学,江苏 常州 213000)
1 教学困扰
随着课程改革的深入和高考命题指导思想的调整[1],数学高考命题的方向和难度有了明显的变化,特别是高考压轴题,由于其内容的综合性、方法的非典型性、思维的深刻性、思路的隐蔽性,学生普遍反映想不到解题方法,甚至有的教师看了标准答案后也不知如何讲清解题的思路,更不用说如何利用它提升学生的解题能力.数学题目是无限的,课堂上教师讲解的题目和学生练习的题目都是有限的,如何以有限的题目去应对无限的挑战呢?新课程背景下师生对数学解题课堂教学水平有了更高的追求,希望不但“知其然”而且“知其所以然”,了解数学解题中更多确定的、规范性的要素,掌握寻找解题方向的常见路径,因此目前普遍运用的题型识别教学已越来越不能满足学生和高考的需求.
笔者认为解决以上困扰的关键是在指导学生掌握寻找解题方向的常见路径的基础上,以“题眼”为起点运用逻辑推理寻找到达结论的路径,或以“模型”为“子目标”运用逻辑推理探索由条件变形为“模型”的路径,从而确定解题方向,并为师生的解法提出合理的、清晰的“辩护”,从而在“辩护”中展示自己的思维过程,提高学生的解题能力[2].笔者以一道模考题为例进行了设计和教学试验,学生反响强烈,寻找解题方向的思路更明确了,确定函数值为相应符号点的方法更精确了,在后续考试中相关题目的得分率显著提高.
2 教学实录
例1已知实数a>0,函数f(x)=xlna-alnx+(x-e)2,其中e是自然对数的底数.
1)当a=e时,求函数f(x)的单调区间;
2)求证:f(x)存在极值点x0,并求x0的最小值.
(2022年江苏省苏州、无锡、常州、镇江四市一模数学试卷第22题)
2.1 寻找解题方向路径1:观察“题眼”,“顺藤摸瓜”
师:第1)小题比较简单,大家做得很好,老师就只提一个问题:为什么求当a=e时,函数f(x)的单调区间,而不是求a取其他值时函数f(x)的单调区间,这里体现了命题者怎样的考量呢?
生1:因为e是特殊值,所以当a=e时,f(x)中相应的系数值好求!
师:e是特殊值,而当a=1时,f(x)中相应的系数值更好求啊,是否还体现在其他方面?
生2:f(x)中对数函数及对数式中的底数是e.
师:为什么题目条件中,函数f(x)=xlna-alnx+(x-e)2中的(x-e)2没有按常规展开?
生3:命题者释放了“善意”:x=e是f(x)=xlna-alnx+(x-e)2的零点,即f(e)=0.
生4:在对f(x)求导后的式子中应保留括号,即对(x-e)2整体求导,得
这样容易发现当a=e时,x=e也是f′(x)的零点.
生5:老师,我找到求解方向了!令f′(x)=g(x),则
从而f′(x)在(0,+∞)上为增函数.又

当a∈(0,e)时,h′(a)>0,h(a)单调递增;当a∈(e,+∞)时,h′(a)<0,h(a)单调递减.因此,当a=e时,
[h(a)]max=h(e)=0,
即
f′(e)≤0.
我只能做到这里,下面就做不下去了.
师:我们知道,解题的本质就是在条件和结论之间架起连通的桥梁.前面我们从条件出发,其实也可以从结论向条件前进,只要二者在某处相遇即可.如何才能证明f(x)存在极值点x0呢?
生6:只要证明f′(x)存在零点,通常的思路是运用零点存在定理,即在某个区间内找到两点,使f′(x)的值异号.现在我们已经得到f′(e)≤0,那么只要找到一个x1,使得f′(x1)≥0就行了,但这个x1我不会找.

这里不等式u(x)>0是易求解的不等式就好了.
师:说得很好!但如何找到相应的不等式u(x)>0呢?观察函数
含x的式子只有两项,将其中哪一项进行放缩呢?放缩后得到的不等式容易求解吗?
生8:因为x>e,所以
只需取
就满足f′(x1)≥0.由前面知f′(e)≤0和零点存在定理可得:存在x0∈[e,x1),使得f′(x0)=0,且当a=e时,x0=e,故x0的最小值为e.
师:生8完全正确.谁能总结一下前面的解题思路?
生9:第一步,依据在审题时捕捉命题者释放出来的“善意”,发现x=e是此题的特殊值,它不仅是f(x)=xlna-alnx+(x-e)2的零点,且满足f′(e)≤0,因此是此题的“题眼”;第二步,根据x>e,对f′(x)进行放缩得到
f′(x)>u(x)≥0,
其中不等式u(x)≥0是容易求解的不等式,找出它的一个解,再运用零点存在定理可证得存在x0.
师:总结得非常好!求解导数压轴题的一个切入口就是捕捉命题者释放出来的善意,寻找“题眼”指引方向,依据解题子目标:容易求解的不等式u(x)≥0,“精确”放缩确定“点位”.此题为什么是缩小,而不是放大呢?何时是放大呢?
生10:此题的任务是找到一个x1,使得f′(x1)≥0,因此可将f′(x1)缩小;如果找到一个x1,使得f′(x1)≤0,那么就应将f′(x1)放大.
师:放缩的方法可能不止一种,但要放缩适度,保证所得到的新不等式的解能满足原来的不等式.
评注俗话说“无巧不成书”,许多数学题的条件(或结论)有其区别于其他题目的内部特殊结构或特征.若能找到它的特殊性,则有助于我们发现珍藏解题思路宝库的窗户.数学题是人来命制的,因此题目或明或暗地体现了命题者的意图与设想,寻找命题者留下的编制“痕迹”与“破绽”,如x=e就是命题者留下来的“破绽”,也是了解题目信息的窗口,更是此题的突破口,因此称其为“题眼”.从“题眼”入手,既可窥一斑而见全豹,理解把握题目的本质,又可尽快领悟命题者的意图,感受其内心思维活动或释放出来的“善意”.因此,本方法的关键是先寻找到“题眼”,并以此为推理的起点,寻找解题方向,再“精确”放缩锁定“点位”.
2.2 寻找解题方向路径2:心有“模型”,“推理成真”
师:证明函数f(x)存在极值点的常规思路(或模型)是什么?
生11:要证明f(x)存在极值点,即证明f′(x)存在零点且在零点两侧异号,因此先求
而f′(x)是关于x的分式,且定义域为(0,+∞),故只需考虑分子对应的二次函数:令
t(x)=2x2+(lna-2e)x-a=0,

x1<0 令x0=x2,f(x)的单调性如表1所示: 表1 f (x)的单调性 下面用换元法求导证明x0的最小值为e即可,此方法有点烦琐,但我不知道怎么改进. 师:每一道数学题目的解题方法可能不一样,但思考的基本方向主要有两个,即“形”和“数”.我们先从“形”的方向来考虑改进,哪位同学能给出思路? 师:哪位同学能从“数”的方向考虑改进? 下面的任务就是消去参数a,而且我们想要得到的是一个含有“≥”的不等式,就是要求右边式子a-x0lna对应函数的最值.记u(t)=t-x0lnt,可求得u(t)的最小值为 u(x0)=x0-x0lnx0, 从而 即 又因为x0>0,所以 2x0+lnx0-(2e+1)≥0. 设v(t)=2t+lnt-(2e+1),可证得v(t)正是我们要寻找的函数. 评注归纳并构建解题模型是由实践形成认识的过程,是用有限道题目的讲解去应对考试命题中无穷道备选题的重要手段,更是数学思想方法形成的基础和中间阶段.解题中以归纳好的常见解题模型为解题子目标,如同下棋用棋谱作为目标牵引一样,有利于提升学生观察和思考的视野,让学生在更高的平台上思考问题,有预见地、主动地、明确地进行解题方法设计,以已有模型为目标借助逻辑推理、猜想等手段探索解题的思路,形成高质量的解题范式,快速提高学生的解题能力,为学生形成数学思想提供有力的支撑.因此,选择适当的“模型”为推理的“终点”,引导我们探索“思路”,既是认识指导实践的过程,也是提升学生逻辑推理能力的过程. 数学解题是解题者自己再发现与再创造的过程,其解法的获得过程是内隐的、混沌的、模糊的,甚至是偶然的,常依赖解题者个人解题经验的积累.而要提高学生的解题能力,就要在解题教学中探寻自然的、平常的解法产生路径,从而暴露解题者的思维过程,明确解题方向的规律,以便让所有的学生都有机会学会解题. 本节课尝试寻找两条解题方向路径:一是从题目本身特征出发.因为数学题是世界文化艺术精品,是人类对自然认识的表达,对题目条件与结论的设置体现了命题者对数学的整体理解和感悟,并蕴藏在“题眼”中,因此我们借助逻辑推理的力量理解题意,就能透过“题眼”“看穿”命题者的意图,提升学生对题目解题方向的感知和预判能力,顺利找到题目的解法.二是以平常积累的题型为基础.如同围棋机器人“阿尔法”一样,搜寻与求解的题目匹配的目标模型,借助逻辑推理的力量揭开笼罩在数学问题上的神秘面纱,依据数学的知识对解题的方法、方向进行判断、选择,寻找题目条件与结论之间的逻辑联系或转化轨迹,把题型作为指引解题方向的“灯塔”,以题型特征为牵引向目标逐渐靠近,在推理的过程中让学生看清问题的本质,让学生的思考有章可循并不断深化,感悟数学思想方法的精髓,提升学生解题的化归能力和思维品质,提高学生独立思考的思维能力,实现快速解题的目的[3]. 要让学生学会解题,就要暴露解题者的思维过程,就需要借助逻辑推理的力量为解法寻找合理、清晰的“辩护”,因此逻辑推理是打开数学解题之门的钥匙.

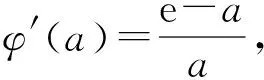

3 教后反思
