在引导反思中促进核心素养的提升

陈海珍

(邵武第一中学,福建 邵武 354000)

反思是指学习者对自身数学认知活动进行周密且有批判性的回顾、反省、抽象、概括的过程,是个体进行自我探究、自我调节、自我监控,从而获得数学学习幸福感与成就感的能力.反思性学习可使学生在心理上拉起一道“警戒线”,表现出优良的批判性、深刻性的思维品质,成为一个自律的学习者,主动监控自己学习活动的过程,从而对各种解决问题的方案进行评价并进行最优处理.《普通高中数学课程标准(2017年版)》中将“反思”提到了应有的高度,即做题是解决问题的过程,包括描述问题、教学表达、建立模型、求解模型、得到结论、反思完善;体现数学学科核心素养的4个方面有情境与问题、知识与技能、思维与表达、交流与反思——主要是指能够用数学语言直观地解释和交流数学的概念、结论、应用和思想方法,并能进行评价、总结与拓展.教学实践表明,引导学生进行反思性学习,不仅能驱动学生主动反思自身的学习过程,多角度地对数学问题进行思考与探究,改善学习策略,培养元认知能力,而且能促使学生将原有知识迁移到新情境中解决问题,由浅层学习迈向深度学习,促进学生情感与思维向深度发展,进而提升数学核心素养.

1 在反思中内化,使“本质”更突出

数学概念是教学的重点与难点,具有高度的抽象性.在抽象概念的过程中,教师不仅要让学生亲历概念的生成过程,还要引领他们运用已学的知识、经验与方法对所学的概念进行反思.这种具有深度思维的学习活动,不是对概念的简单识记与模仿,而是在理解的基础上对概念进行分析、比较、辨别、评价,在具有深度思维价值的数学学习中掌握概念,深化学生对概念内涵与外延的理解,优化认知结构,使其对抽象概念的认识从感性上升到理性,实现思维进阶,进而促进数学核心素养的发展.

案例1人教A版《普通高中教科书·数学》(必修第一册)“古典概型”教学片断.

在学习了“古典概型”定义后,教师引导学生反思:

反思1请同学们思考本节课开始引入的问题:一个袋子里装有质地、大小均相同的4个小球,分别是编号为a,b,c的3个红球与编号为d的1个黑球.张明和林东玩摸球游戏:从袋子里一次性随机取出2个小球,如果取出的球颜色一样,则张明获胜,否则林东获胜.大家觉得此游戏是否公平呢?这是“古典概型”问题吗?请说明理由.

反思2如图1,向一个圆的内部随机投一颗豆子,这颗豆子等可能地落入圆面内任意一点.它是“古典概型”吗?请说明理由.

图1 图2

反思3如图2,某人随机向一个靶心射击,此试验有如下几种结果:“命中10环”“命中9环”“命中8环”“命中7环”“命中6环”“命中5环”与“不中环”.它是“古典概型”吗?请说明理由.

案例1中,教师提出了3个经典问题,引领学生比较、判断.在反思1中,教师故意让红球、白球的数量相差大一些,旨在让学生难以凭直觉获得“游戏是公平”的结论,以此激发学生的探究兴趣.通过反思2与反思3,教师让学生认识到“古典概型”定义中“有限性与等可能性”这两个基本特征缺一不可.通过反思,促进了学生对“古典概型”内涵的理解.

在课堂教学中,教师应为学生提供丰富的背景知识,引领他们进行反思性学习:一是创设问题情境,让学生通过思考获得体验与感悟,积累基本活动经验;二是引导学生进行类比反思,让学生通过分析、比较、归纳等“再认识”活动,把握概念的本质特征,深化对概念的理解,从而提升数学抽象、逻辑推理等核心素养.

2 在反思中感悟,使“纠错”更深刻

由于受年龄特征、思维水平等因素的影响,学生在数学学习过程中难免会产生一定的偏差.对于学生易错的问题,不少教师采取“告诉”的办法,直接告诉错误的原因和正确解法,学生似乎懂了,但过后仍“旧病复发”.其原因是这种单刀直入的讲评往往使犯错的学生处于一知半解的状态,没能真正认识到错误的本质.教学实践表明:对于学生易错的知识点,不能仅仅依赖正面的示范与不断重复的训练,应该变“告诉”为“自纠”,即以自身的反思构建起对错误的认识.因此,教师要适时为学生搭建“犯错”的平台,引导学生对解题过程进行再思考,让学生在对比正误中,寻找出错的根源,在“顿悟”中自我纠错,并获得新的规律与结论[1].这样有助于学生跨越学习“高原”,积累基本活动经验,发展逻辑推理、数学运算等核心素养.

案例2已知函数f(x)=Asin(ωx+φ)(其中A>0,φ>0)的部分图象如图3所示,则当x∈(0,2π)时,使等式f(x)=f(0)成立的x的取值集合是______.

图3

这是笔者所在学校高三一轮复习单元考中的一道试题,学生得分率较低.为了让学生在“顿悟”中自我纠错,教师没有直接指出错因,而是引导学生反思.

教师将学生中比较典型的一种错解进行投影:

错解由图象可得A=1,ω=2,从而

f(x)=sin(2x+φ).

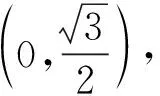
故

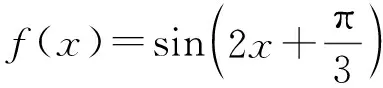
因为f(x)=f(0),所以

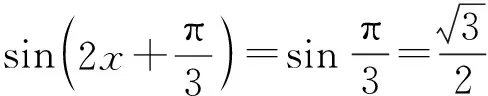
又因为x∈(0,2π),所以

教师不动声色,引导学生反思.

反思1以上解法是否正确?如果有错,那么错在何处?请说明理由.

师:观察函数图象,你有什么发现?

师:好!能把握图象的特征,利用图形验证.

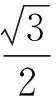
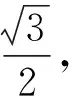
接着,教师将学生中的正确解法进行投影,进一步引导学生反思.

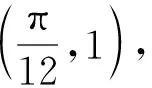
故

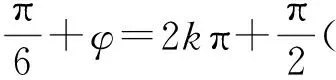
即

从而

(限于篇幅,余下解答过程略.)

反思3以上方法为何不会出现增解呢?

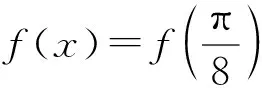
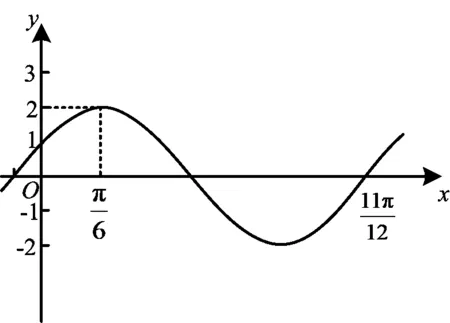
图4

通过展示学生的错解,引导学生在合作、交流中探寻出错的根源,让学生原始的隐性的错误认知“暴露”出来.通过正误辨析,修正错误,不仅提高了学生思维的严密性,提升了自我监控能力,还提炼出了带有普遍性的规律,促进了深度学习,发展了数学运算、逻辑推理等数学核心素养.

3 在反思中延展,使“迁移”更自然

在教学中,教师应引导学生多视角、多维度地反思对数学定理、公式等规律的推导过程、思维策略.可引导学生反思问题特征,领会问题的实质,并对原问题进行引申与拓展,这样可将解决问题的方法与策略迁移到更广阔的平台,使学生在具有深度思维价值的学习活动中达到思维的进阶,提升数学核心素养.

案例3在推导了椭圆与双曲线的标准方程之后,教师有意识地引导学生对“椭圆与双曲线的标准方程的推导过程”进行反思.

反思1对于椭圆与双曲线定义,应怎样用符号语言进行表示?

反思2由等式

推导出了椭圆方程;由等式

推导出了双曲线方程.大家想一想,我们还可能对哪些方程进行推导呢?

反思2使学生产生了强烈的探究欲望,思维顿时活跃起来.

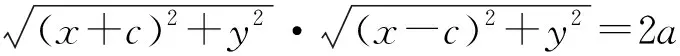
教师设置思维含量高的问题,能有效地驱动学生进行反思.反思与探索的过程,为学生汇聚了解决数学问题的正能量,使学生的思维更深刻,掌握知识的层次更有广度与深度,提升了学生将所学的数学知识迁移到新的问题情境中的能力[2].这种自省式的反思一旦成为学生的主动行为,“深度学习”必然不断取代“浅层学习”,从而促使他们以高远的观点、宽广的视野思考问题、解决问题,让有限的课堂“生长”出学生无限的能力,达到提升学生数学抽象、数学建模、逻辑推理等核心素养的目标.

4 在反思中浸润,使“经验”更稳固

学生对知识的理解,需要通过归纳总结得以深化,因此引导学生进行阶段性反思是提升学生学习效益的保证.可引导学生构建该阶段的思维导图,引导学生对本阶段的概念、公式、定理和法则进行归纳,厘清相近概念、法则之间的逻辑关系;有针对性地设计“纠错练习”,引导学生在解决问题的过程中不断反思,以达到识错、纠错、防错的功效.例如,学习了“直线的方程”这节内容后,教师可引导学生做如下反思:1)反思知识结构:引导学生总结直线方程5种形式之间是如何相互转化的.2)反思易错点:在求解直线方程时,如果没有给出斜率,那么应该讨论直线的斜率是否存在;直线的截距式方程不能表示过原点的直线,因此运用其方程求解时,如果不能确定截距能否等于0,那么应加以讨论.3)反思数学思想方法:引导学生运用“坐标法”对本单元内容进行串联,深化对解析几何基本思想的认识;引导学生反思、归纳本单元内容的主要数学思想方法:数形结合思想、分类讨论思想、直接法、待定系数法等.引导学生对单元的知识和方法进行充分反思,有利于知识的内化与迁移,有利于学生从整体的“高度”驾驭相关知识,使学生的认识从感性、模仿的层次螺旋上升到理性、创新的层次[3].

毋庸置疑,培养学生的反思能力不可能是朝夕之功,需日积月累、循序渐进、逐步提升.因此,教师应把握反思的契机,引导学生进行反思.通过反思性学习,培养学生良好的思维模式,不断提升学习能力与元认知水平.唯有如此,才能促进学生的思维向高阶发展,从而让数学核心素养落地生根.