经历问题解决全过程 在课堂中落实深度学习
2023-09-26徐智愚
徐智愚
(崇明中学,上海 202150)
章建跃博士认为,高中数学学科的题海大,“减负增效”是时代发展赋予每一位数学教师的责任和使命[1].深度学习是学习者能动地参与教学的总称.要改变课堂,必须从改变教师的观念开始.教学从无趣到有趣,让学生从被动变为主动,真正回归“学生主体”的角色,深度学习就是促进课堂转型的支点,使得学生从单纯的、封闭的、缺乏挑战性的活动,走向复杂的、开放的、探索性的学习任务的完成,深刻理解数学问题的隐含内核,掌握并体会数学问题的思想方法,亲身经历数学问题的探究过程,能够综合运用概念、知识与方法创造性地解决问题,进而落实深度学习.本文试以解析几何高考题中“点的个数”问题为例,通过教学实践,浅谈一些体会和思考.
1 渗透问题解决方法,感受深度学习的乐趣
例1点P在直线l:y=x-1上,若存在过点P的直线交抛物线y=x2于点A,B,且|PA|=|AB|,则称点P为“β”点.下列结论正确的是
( )
A.直线l上所有点都是“β”点
B.直线l上有限点为“β”点
C.直线l上所有点都不是“β”点
D.直线l上有无穷多点是“β”点
(2009年北京市数学高考理科试题第8题)
师:你为什么选D?
生1:取较多特殊点进行“计算猜想”,发现直线l上有很多点满足题设条件,故选D.
师:很好!猜想往往能帮助我们发现问题的结论、找到解决问题的途径.其他同学有没有不同的意见?
生2:生1取较多特殊点进行“猜想”,也有可能“所有点在直线上”.我认为选项A和选项D都有可能性.
师:讲得太好了!“猜想”是带有想象力的预测.生1排除了一种可能性,即“所有点在直线上”,到底选A还是D?
生3:简单推理后选A.
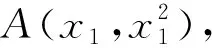

图1
整理得
师:生3的思路清晰,推理严密,非常好!由生3的解法,我们是否可以用类比的方法改编题目,使得直线上有无穷多点是“β”点?
学生处于“愤”“悱”的境界,教室里非常安静,只有学生在纸上书写的“沙沙”声.师生共同得到了如下的结论:
结论1点P在直线l:y=x-b(其中b>0)上,若存在过点P的直线交抛物线y=x2于点A,B(两点可以重合),且|PA|=|AB|,则称点P为“β”点,此时,

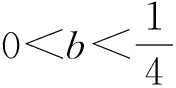
证明把y=x-b代入y=x2,整理得
x2-x+b=0,
从而
Δ=1-4b.

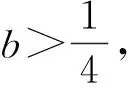
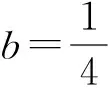
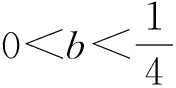
因此,结论1成立.
2 调整问题解决方案,优化深度学习过程
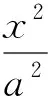
(2022年上海市数学春季高考试题第11题)
问题1如何解决例2?
生1:题目的形式结构类似于向量的数量积,可逆向构造向量的数量积来解决.

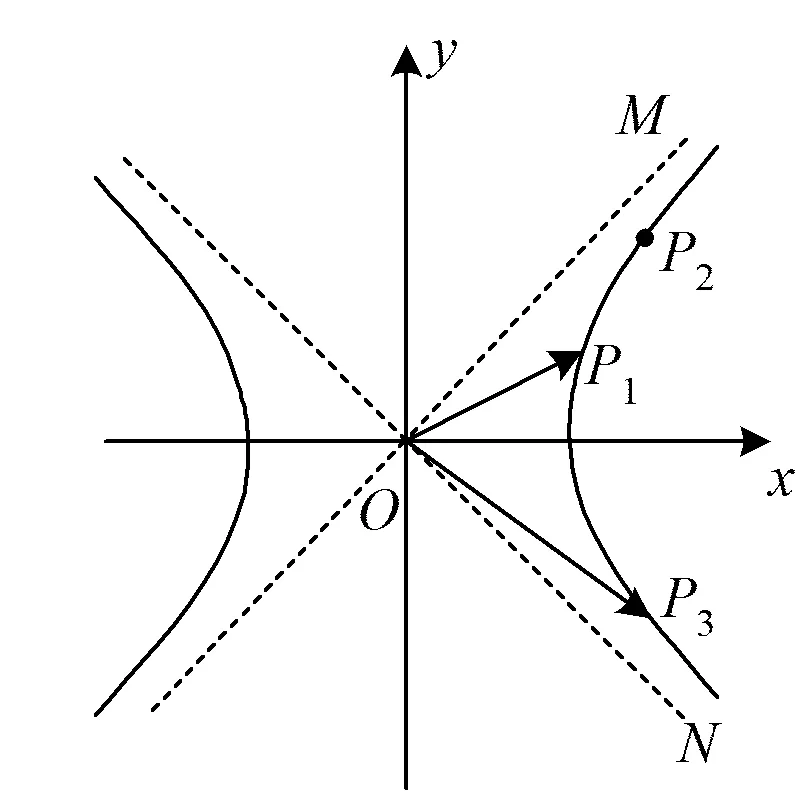
图2
∠MON≤90°,
亦即
∠MOX≤45°.
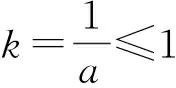
故
a≥1.
师:生1是逆向构造向量的数量积得出∠P1OP3恒为锐角,体现了逆向思维和数形结合的思想.
学生对上述解法议论纷纷,有学生认为,生1这种解法没有创新.很自然地,笔者提出了下列问题:
问题2能否发现其他解法?

师:“三角换元”也是解析几何中的一种重要的思想方法,而且往往可以使得变量范围“缩小”.
这时生3“补充”:曲线是否可能存在3个点满足x1x2x3-y1y2y3>0?
生3的“补充”已经“偏离”了笔者的“轨道”,但通过反思,师生共同发现并解决了新的问题、新的推广和新的结论:
问题3类似题设条件,“曲线是否可能存在3个点满足x1x2x3-y1y2y3>0,求a的取值范围”,那么有限个点呢?任意多个点呢?可能吗?
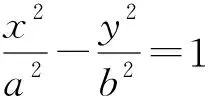
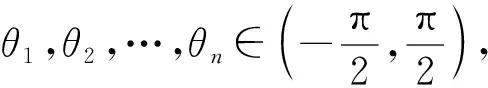
x1x2…xn-y1y2…yn
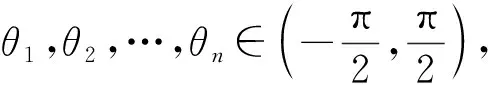
0 -1 只要an-bnsinθ1sinθ2…sinθn>0恒成立,即 亦即 例2为推广1的一个特例,只需取b=1,n=2,可得a≥1. 例3设平面直角坐标系中的点集Ω={(x,y)|(x-k)2+(y-k2)2=4|k|,其中k∈Z}. ①存在直线l,使得Ω中不存在点在l上而存在点在l的两侧; ②存在直线l,使得Ω中存在无数个点在l上. 则下列判断正确的是 ( ) A.①成立,②成立 B.①成立,②不成立 C.①不成立,②成立 D.①不成立,②不成立 (2022年上海市数学秋季高考试题第16题) 对于命题①: 活动1请列出任意两个相邻圆⊙Ck,⊙Ck+1的位置关系的数据分析表,其中这两个圆的圆心距为|CkCk+1|,半径和为Rk+Rk+1.生1列出的数据分析表如表1所示: 表1 ⊙Ck,⊙Ck+1位置关系的数据分析表 活动2从表1中你发现了什么?你有什么新的结论? 生2:随着k的增大,有无数个圆相离,当k≥4时,任意两个相邻圆相离. 生4:随着k的增大,有无数个圆相离,而且当k≥4时,任意两个相邻圆相离,而且这些相邻圆相离的距离越来越大. 师:我们还知道,点集Ω:(x-k)2+(y-k2)2=4|k|所对应的图形关于y轴对称(过程略). 生5:由上述思考可知,可取一个足够大的数k,必存在一条直线y=c(其中c≠0),“穿过”y轴左右两边、对称的4个相邻的且不相交圆的“空档”,使得命题①成立. 活动3不用表格中的数据分析,有没有其他的方法呢? 生6:易知点集Ω:(x-k)2+(y-k2)2=4|k|所对应的图形关于y轴对称. 对于任意k∈Z+,两个相邻圆: ⊙Ck:(x-k)2+(y-k2)2=4|k| 和 ⊙Ck+1:[x-(k+1)]2+[y-(k+1)2]2=4|k+1| 师:太好了!生6的解法使得我们从直观的观察数据分析表上升到严密的逻辑推理论证. 对于命题②: 活动4探究第②个命题,并说明你的理由. 生7:⊙Ck:(x-k)2+(y-k2)2=4|k|与直线ax+by+c=0(其中ab≠0)的距离为 生8:生7的推理不严密!没有从直观上升到逻辑.我是从极限的角度来说明的,即 活动5从生7和生8的推理中,你能判别第②个命题的真伪吗?说明你的理由. 生9:当k趋向于无穷大时,有无数个圆和直线ax+by+c=0(其中ab≠0)相离;反过来,即存在一个足够小的数k,使得有限个圆和直线ax+by+c=0相交,使得命题②不成立. 活动6是否可以改变题目条件,使得命题“存在直线,使得Ω中存在点(0个、有限个、无数个或任意一个)在l上”成立? 在师生的共同探究下,回到最基础的概念,得出了如下的方法:原问题转化为判定点集Ω中的圆与直线ax+by+c=0(其中ab≠0)是否有公共点,即转化为判定圆和直线相交(或相切),即判定 的整数解的个数. 化简上式,得 f(k)=b2k4+2abk3+(a2+2bc)k2+2ack -4(a2+b2)|k|+c2≤0. (1) 1)当b≠0时,b2>0,由代数基本定理:在复数范围内方程f(k)=0有4个根. 如果它有一个虚根,那么必定存在一个对应的共轭虚根,因此方程f(k)=0的实数根个数为0,2,4个(不妨假设f(k)=0有4个实根,分别为t1,t2,t3,t4,且t1≤t2≤t3≤t4). 由标根法可知:f(k)≤0的解是t1≤k≤t2或t3≤k≤t4;ti≤k≤tj(其中i,j=1,2,3,4,且i≤j),k∈φ .因此,整数解的个数至多为有限个. 2)当b=0时,a≠0,则a2>0,则式(1)转化为 a2k2+2ack-4a2|k|+c2≤0, 证明方法同情形1),得整数解的个数也至多为有限个. 综上所述,当k∈Z时,整数解的个数为有限个或不存在(至多为有限个).故命题②错误,选B. 基于核心素养的深度学习把问题置于重要地位.深度学习将学生的思维过程与教学过程融为一体,在教学中全景呈现问题解决的思维过程.在课堂中落实深度学习,必须让学生主动参与学习活动,亲身经历问题解决的发现、发生、发展全过程,从而形成学生丰富的内心体验.通过教师设计的学习主题、挑战性学习任务或活动以及持续性的学习评价,吸引学生主动、全身心地投入问题探究活动之中,感受深度学习课堂的乐趣,激发学生内在的学习动机,不断生成成就感和效能感. 在课堂中落实深度学习,教师应渗透问题解决的数学思想方法:观察、试验、联想、类比、演绎、归纳、分析、综合、猜想等,师生共同对问题核心进行有深度、有宽度的加工,搭建问题解决的“脚手架”.如在例1中,教师引导学生用类比的方法发现并解决题目中创新的数学问题,能让学生充分感受数学思想方法的创造性,让问题探究过程更加新颖有趣、富于创意、生动活泼. 深度学习更强调思维的活跃度和思考的深度.发现并提出适切性、高质量、有深度的问题,学生在环环相扣的问题串的引领下开展深度学习.同时,深度学习课堂要求教师反思教学中存在的问题,及时调整问题解决方案,研究并解决教学中的核心问题,以优化深度学习课堂过程.如在例2中,如果没有对“生1这种解法没有创新”和生3的“补充”进行反思,就没有学生的“追根溯源”,就不可能发现例2中隐含的一系列新的问题、推广和结论.没有反思,学生的理解就不可能从一个水平升华到更高的水平[2]. 深度学习课堂要从学生的立场出发,直指有深度、有意义的学习,又要从教师的角度切入,在对教学做系统思考和相应研究的基础上进行教学设计.教师应积极探索基于问题导向的启发式、探究式、互动式、体验式的学习活动,形成有个性的、有深度的、有意义的、创新的、多元化的课堂活动方案,通过一系列的活动与问题,为学生搭建深度学习的阶梯,帮助学生透过表象去感悟问题背后的原因、意义等,最终促进学生深度学习的发生. 在课堂中落实深度学习,教师准备及时、合适、富有挑战性的问题是前提,要敢于提出问题,即使教师在课前还未曾准备过的变式问题,也要敢于提出来.留给学生充足的自主学习时间是关键,史宁中教授说过,素养的形成和发展,在本质上,不是靠教师“教”出来的,而是靠学生“悟”出来的[3].教师要放慢上课的节奏,给学生充分“悟”的时间和空间,使得那些反应慢但是思考比较深刻的学生的思维火花也能“燃烧成炬”.教师适时串联和反刍是重点,在学生最需要的地方搭建合适的“脚手架”,既包括对相关知识内容的讲解、拓展,也可能是相关内容的提供或让学生讨论,这些都是让学习更加深入的好方法.教师的有效设计和鼓励是根本,把要讲的内容转化为符合学生特点的问题或任务,让学生在问题解决的过程中形成深度学习的经验和能力,要不断给学生的鼓励,让学生感受到自己是具有学习能力的.当学生相信自己会学习、会思考、会讨论、会探索的时候,他们的学习才可能深入下去.
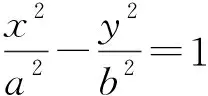
3 创建问题解决活动,挑战深度学习任务

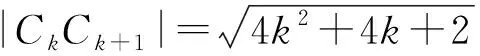
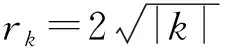

4 结束语
