民族数学视域下的平面图形镶嵌设计

程孝丽, 周建萍

(南苑中学,浙江 金华 321017)

《义务教育数学课程标准(2022年版)》(以下统称《课标》)明确指出,数学是人类文化的重要组成部分,强调了数学与现实世界的关系,提出了会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界.这要求一线教师切实思考除了数学本身的知识体系外的文化范畴,也是目前数学与数学教育研究关注的重要内容.由于民族数学对社会文化的特别关注,受到了国内外研究者的重视,一些学者在实证研究中提出民族数学的教育意义与价值[1-3].

然而如何在学校数学教学中渗透民族数学是值得进一步思考与探究的.有学者以非洲日常用品中的几何变化为例,探讨民族数学的教育学转化问题[4],有学者以我国少数民族的民族服饰和民族工艺品等为例,提炼其蕴涵的对称、变换等数学思想[5],也有学者从藏族文化背景或生活中提炼数学资源,提出藏族数学文化融入小学数学课堂的案例设计原则与依据[6].本研究以平面图形镶嵌为例,探讨如何从民族数学的视角解释数学与现实世界的关系,以及真实情境对学生课堂参与和数学情感的影响.

之所以选择平面图形镶嵌,一方面,考虑到这是几何图形在生活中的广泛应用,除其悠久的历史外,从自然界到人类的镶嵌艺术无不体现了数学文化在自然界和人类文明中的深刻且深远的影响,为素材的挖掘提供了丰富的来源;另一方面,平面图形镶嵌的学习既需要知识层面的研究,即厘清何为平面图形镶嵌以及镶嵌的规律,也需要操作层面的践行与探索,即镶嵌的实际应用.在学生制作平面镶嵌图形的过程中,是理论到实践的跨越,是数学美育的真实写照.作为拓展内容的平面图形镶嵌不在学业水平测试范围内易被忽视,加上教材中的镶嵌素材不够丰富,因此,教师挖掘力度不够,并没有引起广大一线教师的重视.基于此,本研究以平面图形镶嵌为例,进一步讨论如何在学校教学中实现民族数学的教育学转化问题.

1 民族数学中的平面图形镶嵌

民族数学(或民俗数学)是指向特定文化中的数学元素、数学思想和数学实践,是(多元)文化数学的进一步发展[7],也是数学文化进入学校数学的重要载体.有学者指出,民族数学是社会变化中的实践产物,旨在调和数学思想、知识体系和社会三者关系,在数学教育教学的过程中,应当保持或发挥民族数学特定的文化优势[8].如何挖掘民族数学的素材,以及如何将民族数学融入学校教学是数学教育中亟待解决的问题,也是研究民族数学的意义和关键所在.借鉴已有学者的分类方法,笔者从文化传统和日常生活两个方面展开素材的挖掘与教育学转化的研究[9].

1.1 素材的挖掘

图1是日常生活中较为常见的地面铺砖,为单一的(正)多边形镶嵌图形.图2是生活用品竹编,相比于前者,它在图形构造上较为复杂,是两种正多边形(正三角形和正六边形)的组合镶嵌.图3是传统工艺中流行的窗户花格,是对竹编中的两个正多边形镶嵌一般化的结果,即两种多边形的组合镶嵌.图4是云南傣族织锦(又称“娑罗布”),这些少数民族的手工织锦图案丰富多彩、颜色鲜明,特别是织锦上的几何纹样是通过实物(如飞禽走兽、花草树木)抽象而成.大部分织锦是几何图案单一或组合镶嵌形式,亦可通过平移、对称、相似等几何变换得到.这既是少数民族人民智慧的结晶,也象征着人们对美好生活的向往和追求.

图1 图2 图3 图4

图5是荷兰艺术家埃舍尔的作品.这位被誉为“错觉大师”的单体镶嵌、双体镶嵌和渐变镶嵌等作品,是在规则多边形(如正三角形和特殊四边形)的基础上,采用了不规则多边形平铺的理论,利用这些具象的基本图形(鱼、鸟、马和骑士等)进行多次的反射、平滑反射、变换和旋转得到美妙、生动的图案,是平面镶嵌艺术的应用和升华.

图6是西班牙的阿尔汗布拉宫的穆斯林设计.这个具有600多年历史的建筑彰显着无处不在的镶嵌艺术,其地砖、天花板等各处的装饰都采用了平面镶嵌,可圈可点的是这些图案仅用圆规和直尺通过平移、对称、反射和旋转等几何变换创作出来,可以说整个宫殿就是数学几何图案的殿堂,这也折射出穆斯林艺术家对数学的狂热,以及通过几何学表达他们对服从数学和推理的宇宙的宗教信仰[10]!

1.2 素材的教育学转化

这些有着不同文化背景的生活用品和艺术作品作为镶嵌素材进入学校教学还要进行一定的教育学转化,也就是说将这些朴素的贴近学生生活的数学元素转化为符合学生认知的逻辑体系.

有学者提出教育学转化时需要注意知识序和认知序.笔者结合镶嵌的教学内容以及知识结构,从学生认知水平的维度对素材进行了梳理.主线是将素材按照由单一的(正)多边形镶嵌到多种(正)多边形组合镶嵌的顺序进行归类,让素材的呈现符合从易到难、由简单到复杂的规律.图1～4都是学生耳熟能详的规则的几何图形镶嵌,其中图1和图4分别是单一的正六边形和菱形镶嵌,学生从生活经验中容易发现地砖和织锦在设计时都满足不重叠、不留空隙的特点,在此基础上,呈现更多的单一(正)多边形镶嵌图片.进而分析图2和图3,即两种正多边形组合镶嵌.在学生经历从单一到组合、由特殊到一般的过程中,探索平面图形镶嵌的本质与规律.最后再呈现图5和图6,由规则的几何图形镶嵌变化成不规则的几何图形镶嵌,从图形抽象又回到图形具象,提高了对概念理解和实际应用(甚至是艺术创作)的双重要求,是图形镶嵌的进一步理解与运用.

暗线是根据素材的用途(如欣赏、典例剖析)决定是否需要把实物转换成教学所需的形态,即实物抽象与提炼成几何图形.图2作为研究两种正多边形镶嵌的基本图形,在教学中要将其几何化,让学生对两种多边形镶嵌有更直观的感受.图5是在规则的多边形基础上通过裁剪、平移和对称等方式转化为更复杂的优美的具象基本图形,一般此类型的镶嵌作品多以正三角形、矩形或菱形等作为基本图形.

像这样进行转化后的民族数学不仅具有教学形态,使学习内容更贴近学生的生活与文化背景,而且体现了多元的民族文化,展示了数学之美.

2 教学实践与成效

2.1 实施过程

笔者以所在学校的九年级学生为授课对象,开展了“美丽的镶嵌”的教学活动.具体而言,笔者以问题为导向设计了4个环节和3项探究活动.

环节1寻找生活中的镶嵌.

呈现大量生活中的镶嵌图形(如图1～4),让学生对镶嵌有一个初步、直观的感知.在学生欣赏图片的过程中适当介绍作品的文化背景,让学生感受不同时代、不同文化背景下的镶嵌艺术.笔者选择简单的图1引导学生思考在铺设地砖时应该满足的条件,从而再观察这些图片是否都符合要求.在引出镶嵌概念后,进一步指出图1中镶嵌的基本图形,追问以下两个问题:只有边长相等的正三角形能形成平面镶嵌图形吗?正五边形、正七边形、正八边形呢?由此展开下面的探究活动.

环节2探索平面镶嵌的本质.

在第一环节呈现的图1～4中有单一的(正)多边形镶嵌也有组合的(正)多边形镶嵌,因此学生知道这个结论,但具体到哪一种正多边形或者哪两种正多边形组合是不明确的,需要学生在问题引导下进行实验操作,在探索中发现平面镶嵌的规则.

活动1探究用一种正多边形进行平面镶嵌.

问题1仅用一种正多边形进行平面镶嵌,哪些正多边形符合镶嵌的条件?

问题2用正n边形进行平面镶嵌的条件是什么?

问题3除了正三角形,能用任意一个三角形镶嵌成平面图案吗?任意的四边形呢?

评注通过活动1,教师帮助学生梳理探究的方法与思路,从形的角度通过实验操作发现结论,再结合数的角度分析正多边形的周角和内角之间的关系(如表1所示),为活动2提供研究方向.在活动1后充分发挥心理学中正向迁移的积极作用,紧接着开展探究活动2,通过类比、迁移让学生合作探究两种正多边形的组合镶嵌的规则以及组合的可能性.

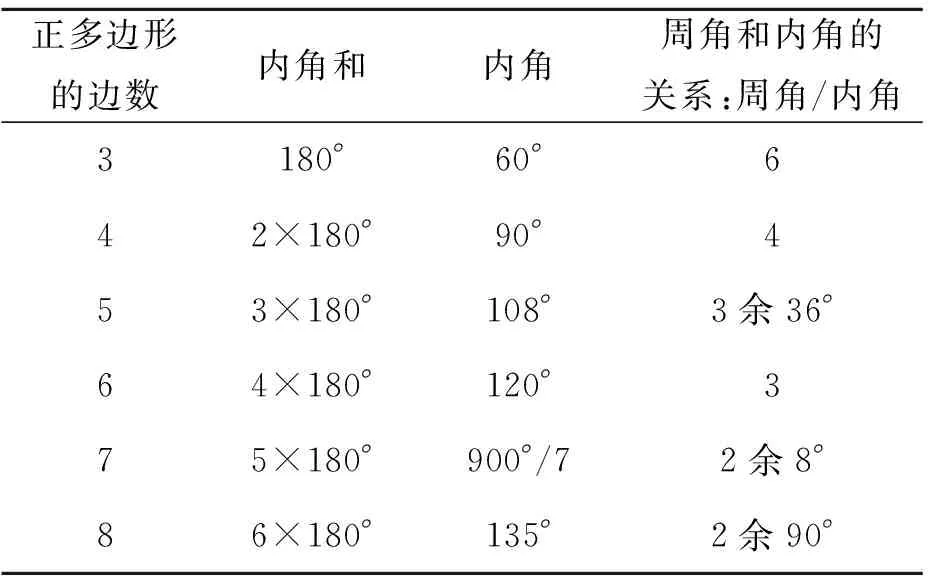
表1 正多边形的周角和内角之间的关系

活动2探究用两种正多边形进行组合镶嵌.

问题4如果用两种正多边形组合镶嵌,哪两种正多边形能镶嵌成一个平面图案?这两种正多边形需满足什么要求?

评注在活动2中,有的小组首先用方程思想解决二元一次方程的不定解问题,再用作图或剪拼的实验方式验证;有的小组则先实验操作,再归纳分析,总结规律.在合作探究中,学生较好地沿用了活动1的方法,从几何操作和方程模型两个维度进行类比探究.

环节3了解平面镶嵌文化.

在两个探究活动之后,学生对平面镶嵌有了更深刻、具体的理解,进而介绍镶嵌问题的历史背景,从整体上让学生对镶嵌的认识更加丰富.从自然界中的有序结构(如蜂巢),到阿尔汗布拉宫奇妙的穆斯林设计(图6),到埃舍尔出神入化的镶嵌图案(图5),到世界上第一个正多边形组合设计的丢勒镶嵌,再到简洁的彭罗斯拼砖,镶嵌的基本图形由简单的几何形状演化为具象的不规则图形,由单一和组合镶嵌演化为单体镶嵌、双体镶嵌和渐变镶嵌等,镶嵌图形不仅经历了漫长的世纪,更演绎了不同的文化.

由贴近生活的简单用品,逐步演化到丰富精美的艺术创作,让学生体会镶嵌自古以来在生活中的广泛应用.看似简单的具象图形镶嵌,其实是复杂的思维过程,除了对规则的基本图形进行图形变换处理,还要整体把握镶嵌的条件,这非常考验该阶段学生的图形思维能力,初步让学生感受镶嵌艺术的复杂性.这一环节的设计也为下一环节的微项目化活动埋下了伏笔.

环节4制作平面镶嵌作品.

这一环节分为两个任务:1)寻找日常生活、建筑等中的镶嵌图形;2)根据活动2的探究结果,设计两种正多边形镶嵌的图形,主要面向接受程度较低的学生;类比埃舍尔的镶嵌艺术作品,自由创作镶嵌图形,主要面向综合能力还不错的学生.第二个任务学生可以独立完成,也可以4人一组合作完成,但需要学生自主研究该类型镶嵌的设计方法与思路.最后进行成果展示,分享设计思路与方法,以及在设计过程中遇到的困难和解决问题的方式方法.

4个环节在具体实施时共用了2.5课时:环节1～3用了1课时,通过两个合作活动探索平面镶嵌的本质与规律,加深对平面镶嵌的认识;通过两个欣赏活动丰富对镶嵌图形的认识,加深对平面镶嵌的应用意识.环节4用了1.5课时,其中上网查资料明确设计方法和确定镶嵌基本图形用了0.5课时,设计作品和作品展示1课时.在整个环节中,内容与环节的设计始终遵循从简单到复杂、由特殊到一般的规律,让学生有梯度地开展实践活动,在实验中收获知识与方法,感受镶嵌的神奇与美妙.特别是最后的制作环节,学生体验了数学家的思维、欣赏了创作艺术家的作品.

2.2 实践成效

根据课堂教学的实际情况以及学生和听课教师的反馈,笔者将课堂教学效果进行简要地分析.

一是教学目标的落实情况.从探究活动的过程与成果可以发现,学生基本掌握了平面镶嵌的概念,且能够通过实验、观察、猜想和分析发现一种或者两种正多边形形成镶嵌的条件和原理.从学生整体的课堂参与度和课后的评价可以感受到学生十分喜欢这样的数学课堂,他们发现“数学源于生活用于生活”原来不是一句标语;这些生活用品居然蕴涵了这么多数学知识;少数民族的人们太厉害了,看似简单的几何图形竟然可以制成如此复杂的织锦;仿佛打开了一扇通向无限可能的大门……不难发现学生对数学的认识在转变.从学生设计的作品(如图7)可以看出学生对镶嵌的学习达到了较好的效果,其精心的设计成果与巧妙的设计方法(综合平移、旋转和对称等方式)说明这些学生对镶嵌的认识远超于其他学生,他们的抽象思维和具象思维也是难能可贵的.

图7

二是学生课堂参与情况.这里的课堂参与主要是指情感参与、行为参与和认知参与.通过观察和统计学生参与数学活动的时间、提问和讨论问题的次数来评价学生的课堂参与度.第1课时主要有两个数学探究活动,活动以问题为导向,在同一个活动中从特殊的正多边形镶嵌探究到一般形式的三角形、四边形镶嵌,在活动之间从单一镶嵌过渡到组合镶嵌,两个活动都差不多用了8分钟时间,让学生充分经历动手操作、发现问题和解决问题的过程.除了探究活动外,学生在环节1和环节3也给予了积极的回应,这些不同文化背景下的镶嵌物品和艺术引发了学生对数学认识“狭隘”的共鸣,在情感上获得支持后学生的课堂参与度显著提高,更愿意融入讨论和实验环节等.无独有偶,也有学者提出将学生的学习环境和文化背景相结合,学生的认知水平、学习兴趣和学习能力都会得到提升[11].

总的来说,学生在情境体验中丰富了对数学的认识,夯实了数学文化的厚重感,在活动探究中锻炼了抽象能力、几何直观和推理能力,在作品制作中培养了创新意识和应用意识.

3 结论与展望

在这样的基础上,应该切实把握民族数学的教育价值,这是回答“为什么要让民族数学进入学校”的问题,也是本研究的目的和意义.

首先,民族数学的融入确实能较好地解决数学教学中文化相关性的问题.民族数学是多元文化数学的进一步发展,其蕴涵的文化背景、价值观念会带给学生多元文化的体验,感受不同民族、不同生活方式以及别样的传统文化,图2和图4分别体现了不同民族的镶嵌物品,使学生感受到数学除了发生在课堂还可以存在并广泛应用于不同种族的生活中,学校数学学习不是学生获取数学知识和方法的唯一来源,学校以外贴近学生生活的日常活动和文化传统也是数学知识和方法的矿藏.在潜移默化中让学生能够体会“数学是源于生活的有趣现象和延伸”,希望学生能够在数学的引领下去探索更神秘、更深邃、更美丽的世界.图5和图6分别体现了艺术、建筑等不同领域中镶嵌的应用,虽是不同文化背景的镶嵌作品但都是图形镶嵌的衍生,蕴涵了平移、旋转和对称等几何变换的思想.因此,在关注民族数学的文化多样性的同时不能忽视各个民族的文化中也会存在相同的数学知识.

其次,民族数学的教学可以发展数学教育的价值标准.数学是一个相对开放的动态的文化系统,不能脱离社会、脱离其文化系统存在.民族数学通过对不同文化中的数学元素、数学思想方法乃至历史发展进行教学展现,帮助学生对数学有一个全面、动态的理解[12].