探析高考真题 明晰备考方向——对2023年全国数学新高考Ⅱ卷试题的评析与备考建议

刘海涛

(芜湖市第一中学,安徽 芜湖 241000)

2023年教育考试中心共命制了6套数学试卷(全国甲、乙卷的文、理试卷和新高考Ⅰ,Ⅱ卷),其中安徽、山西、辽宁、吉林、黑龙江、海南、重庆、云南等8省(市)使用了新高考Ⅱ卷.

高考结束,笔者与学生交流,均反映试卷总体平稳,比预期难度略低,考完也信心满满.《中国高考评价体系》指出,通过设置真实的问题情境,考查学生灵活运用所学知识分析、解决问题的能力,允许学生从多角度作答,使“死记硬背”“机械刷题”“题海战术”的收益大大降低,引导学生的关注点从“解题”向“解决问题”、从“做题”向“做人做事”的转变.

2023年的新高考Ⅱ卷注重能力和素养考查的同时,深化了对德育的考查.与2022年Ⅱ卷相比,难度相当,但结构上更加新颖,更加注重对学生“四基”“四能”的考查,整卷兼具基础性、综合性、应用性和创新性,试题类型分类如表1所示.下面笔者以新高考Ⅱ卷中的部分试题为例,深度探析高考真题,剖析新高考Ⅱ卷的命题特色,总结规律,明晰高考备考方向,给出备考建议.

表1 新高考Ⅱ卷试题类型分类

1 特色试题赏析

1.1 立足基础,考查通性通法

《中国高考评价体系》指出,高考围绕学科主干内容,加强对基本概念、基本思想的考查,杜绝偏难怪题和繁难试题,引导教学重视教材,夯实学生的学习基础,给学生提供深度学习和思考的空间.试卷注重基础知识和基本方法的考查,试题的命制围绕高中数学的基础知识与基本概念展开,如第1,2,4,6,7,8,10,12,13,17,18等题,均为来源于教材例题、习题的改编,只要学生基础扎实,考场上做这些题定能得心应手.

( 2023年全国数学新高考Ⅱ卷第13题)

解法1因为|a+b|=|2a-b|,

即

(a+b)2=(2a-b)2,

则

a2+2a·b+b2=4a2-4a·b+b2,

整理得

a2-2a·b=0.

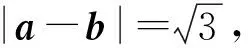
(a-b)2=3,

则

a2-2a·b+b2=b2=3,

故

解法2设c=a-b,则

由题意可得 (c+2b)2=(2c+b)2,

则

c2+4c·b+4b2=4c2+4c·b2+b2,

整理得

c2=b2,

即

1.2 注重综合,考查知识的融会贯通

《中国高考评价体系》指出,素质教育是内涵丰富的全面发展教育.高考要求学生能够触类旁通、融会贯通,既包括同一层面、横向的交汇融合,也包括不同层面之间、纵向的融会贯通.第9题以多选题的形式考查圆锥的内容,4个选项设问逐次递进,前面的选项为后面的选项提供条件,各选项分别考查圆锥的不同性质,互相联系,重点突出,要求学生能够将立体几何的知识交汇融合.第22题将导数与三角函数巧妙地结合起来,通过对导函数的分析,考查函数的单调性、极值等相关知识,需要学生能将导数、函数不等式等知识融会贯通.

例2已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,PA=2,点C在底面圆周上,且二面角P-AC-O为45°,则

( )

( 2023年全国数学新高考Ⅱ卷第9题)

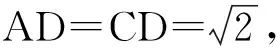
图2

故选项D错误.

综上可知,此题选A和C.

评注该题考查了圆锥的体积、侧面积,二面角的平面角,三角形的面积等知识,是一道立体几何综合试题.该题属于中等难度试题,解答的关键在于牢固掌握立体几何的基础知识、概念和基本方法,解题时综合应用即可.

1.3 关注应用,考查素养与能力

《普通高中数学课程标准(2017年版2020年修订)》指出,在学习数学和应用数学的过程中,学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养.数学来源于生活,又服务于生活,与实际生活结合的数学试题一直是高考的一个热点.第12题以信号传输为情境考查二项分布及其应用,试题设计了两种传输方式:单次传输和3次传输,依次研究各种传输方式得到正确信号的概率,考查了学生对新概念、新知识的理解和探究能力.第19题要求合理平衡漏诊率和误诊率,制定检测标准,试题情境既有现实意义,也能很好地体现数学学科的应用价值.随着“双减”政策的落地实施,教学中教师应注重情境化教学.

例3在信道内传输0,1信号,信号的传输相互独立．发送0时,收到1的概率为α(其中0<α<1),收到0的概率为1-α;发送1时,收到0的概率为β(其中0<β<1),收到1的概率为1-β.考虑两种传输方案:单次传输和3次传输．单次传输是指每个信号只发送1次,3次传输是指每个信号重复发送3次．收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;3次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1)

( )

A.采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为(1-α)(1-β)2

B.采用3次传输方案,若发送1,则依次收到1,0,1的概率为β(1-β)2

C.采用3次传输方案,若发送1,则译码为1的概率为β(1-β)2+(1-β)2

D.当0<α<0.5时,若发送0,则采用3次传输方案译码为0的概率大于采用单次传输方案译码为0的概率

( 2023年全国数学新高考Ⅱ卷第12题)

分析对于选项A,若依次发送1,0,1,则依次收到1,0,1的事件是发送1接收1、发送0接收0、发送1接收1的3个事件的积,它们相互独立,从而所求概率为

(1-β)(1-α)(1-β)=(1-α)(1-β)2.

故选项A正确.

对于选项B,3次传输,若发送1,相当于依次发送1,1,1,则依次收到1,0,1的事件是发送1接收1、发送1接收0、发送1接收1的3个事件的积.它们相互独立,因此所求概率为

(1-β)β(1-β)=β(1-β)2.

故选项B正确;

对于选项C,3次传输,若发送1,则译码为1的事件是依次收到1,1,0;1,0,1;0,1,1和1,1,1的事件和,它们互斥.由选项B知所求的概率为

故选项C错误.

对于选项D,由选项C知3次传输,若发送0,则译码为0的概率为P=(1-α)2(1+2α),单次传输发送0,则译码为0的概率P′=1-α.而0<α<0.5,因此

P-P′=(1-α)2(1+2α)-(1-α)

=α(1-α)(1-2α)>0,

即P>P′.故选项D正确.

综上可知,此题选A,B,D.

评注该题考查了学生的数学阅读能力,将现实情境抽象为数学问题,借助所学统计与概率学知识,根据题设条件介绍的两种传输方式:单次传输与3次传输,依次研究各种传输方式得到正确信号的概率,有效考查了学生应用所学分析、解决问题的能力.

1.4 强调创新,考查思维的灵活性

《中国高考评价体系》指出,素质教育中的智育和以往教育理念中的智育,最大的不同在于其对创新性的强调.通过命题创新,创设新颖的试题情境、新颖的题目条件、新颖的设问方式,考查学生思维的灵活性与创造性.第11题虽考查极值点问题,却不是求极值点或极值,而是将问题设置为函数有极值,逆向研究函数系数的关系,从而有效地考查学生思维的灵活性与创新性.第15题是一道开放性试题,有多个答案,充分考查了学生的创新思维能力.

( )

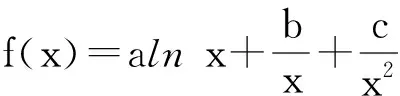
A.bc>0 B.ab>0 C.b2+8ac>0 D.ac<0

( 2023年全国数学新高考Ⅱ卷第11题)

则

b2+8ac>0,ab>0,ac<0.

显然a2bc<0,即bc<0,从而选项A错误,选项B,C,D正确.故此题选B,C,D.

评注解答该题的关键在于对极值点概念的理解,将问题转化为导函数f′(x)在定义域(0,+∞)上有两个变号零点,进而转化为一元二次方程有两个不等正根问题,利用根与系数关系及判别式符号解题.此题有效考查了学生的思维灵活性与创新性,需要学生不断地转化题意,直至问题“水落石出”“柳暗花明”.

2 高考备考建议

2.1 重视“四基”,发展数学关键能力

在高考备考中,师生应重视巩固基础知识、落实基本技能、感悟基本思想方法、积累基本活动经验[1],如将教材中的基本概念、基础知识等按照函数、几何、概率统计等模块进行梳理,形成知识网络体系;按照解题思想,根据数形结合、转化与化归、整体思想、分类讨论等将高考常考题型进行分类,总结常规题型的“通性通法”,注重教材知识的生成过程,善于运用“本原”法解题.这样,我们才能切实有效地提高复习效率,发展数学关键能力和核心素养.

2.2 重视解题,更要重视解决问题

《中国高考评价体系》指出,高考要从“解题”向“解决问题”,从“做题”向“做人做事”转变,这就要求我们在高考备考中,要关注时事,关心政治,注重数学阅读能力的培养,能够从真实的问题情境中抽象出数学模型,灵活运用所学数学知识分析、解决问题,避免“死记硬背”“生搬硬套”“机械刷题”“题海战术”,成为国家需要的、在能力和素养方面有较好发展的学生.

2.3 重视真题,关注高考试题变化

高考试题凝聚着命题者的心血与智慧,是经过命题者反复考量与打磨才成型的,对高考的备考具有导向性与启示性[2].在复习备考中,师生要重视对高考真题的收集、整理、归类、溯源、拓展、推广等,明确其考查的内容、方向、要求,感受高考题的变化趋势与基本态势.关注教育与考试部门发表的有关考试的最新信息,掌握最新的考试动态,研读官方文件与指导性材料,以便科学、高效地备考.