量子Swapping网络中非局域性度量的上界的优化

张 颖,郭志华,贺 衎*

(1 太原理工大学 数学学院,山西 太原 030024;2 陕西师范大学 数学与统计学院,陕西 西安710119)

量子非局域性是一个量子力学的基本概念,它被广泛应用于量子信息处理任务中,如减少通信复杂度、量子密钥分配、私密随机数生成以及与设备无关的纠缠见证[1-6]。从概念上讲,非局域性是一种不能被任何局域隐变量理论所描述的关联,它与纠缠和量子特性等其他现象密切相关,但又有所区别[7]。学者们通过贝尔不等式的方法对非局域性进行了广泛研究[8-13]。但仅通过贝尔不等式的角度去研究非局域性显然是不够的,这是因为存在着无量子特性的非局域性[14]和无纠缠的非局域性[15-18]。Luo等[19]提出了测量诱导的非局域(measurement-induced nonlocality, MIN),并得到了任意维纯态和2×n维混合态的解析解。Mirafzali等[20]研究了任意m×n维两体态的MIN值,获得了MIN的上界计算公式,该上界比文献[19]中的上界更便于计算且更精细。

之后,量子非局域性的研究延伸到量子网络实验上。在量子网络实验中有多个观察者和多个源[21-31],最简单的例子是涉及3个观察者和2个源的量子Swapping实验。如图1所示,Alice、Bob、Charles是观测者,且具有观测算子组{Ax}x=0,1、{By}y=0,1、{Cz}z=0,1, 源S1发送一个两体系统ρAB,源S2发送一个两体系统ρCD,注意Bob的观测算子是作用在ρBC这个两体系统上的。

图1 双局域场景Fig.1 Scenario of bilocality

为了有效捕获该实验中的非局域关联,Zhang等[32-33]量化了该场景下的非局域性,提出了测量诱导的非双局域关联(measurement-induced non-bilocal correlation)这一度量概念,给出了纯态情形下该度量的解析解和混合态情形下的一个上界。但是,该上界不便于计算,对于某些混合态,可以继续细化上界的计算公式以减少计算量。本文将对一类混合态给出比文献[32]中测量诱导的非双局域关联的上界更便于计算的一个上界公式。这类特殊态,就是当边缘态ρBC=ρB⊗ρC中ρB非简并且ρC简并的混合态。

1 测量诱导的非双局域关联

考虑一个有限维的四体系统,对应复希尔伯特空间H=HA⊗HB⊗HC⊗HD,其中HA(HB、HC、HD)是粒子A(B、C、D)的希尔伯特空间,且具有维数m(n、u、v)。令D(H)是H上有界、迹为1的半正定算子的集合。给定由A、B共享的量子态ρAB∈D(HA⊗HB),和由C、D共享的量子态ρCD∈D(HC⊗HD),定义测量诱导的非双局域关联[32]为

NC(ρAB⊗ρCD)=

(1)

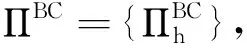
(2)

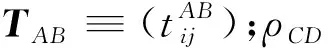
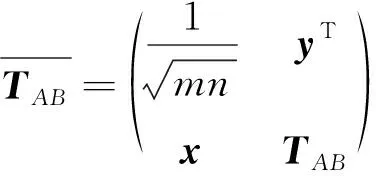
这里x=(x1,x2,…,xm2-1)T。类似地,对y、z和w进行假设,于是有

Zk⊗Wl,

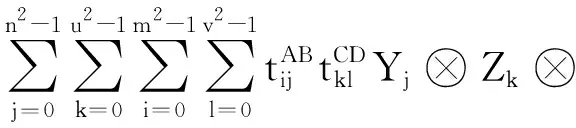
Xi⊗Wl,

对于(2)式中表示的ρAB和ρCD,文献[32]推导了测量诱导的非双局域关联的上界

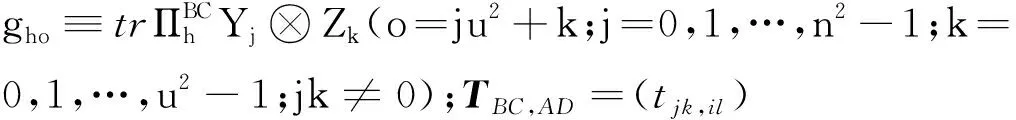
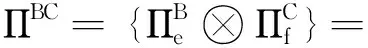
(3)

最后,若ρB和ρC都是非简并且有谱投影{|eB〉〈eB|}和{|fC〉〈fC|},则

式中C≡(cfk)是一个u×(u2-1)维矩阵,且cfk≡tr(|fC〉〈fC|Zk)=〈fC|Zk|fC〉(k=1,2,…,u2-1)。

后面,针对(3)式中混合态情况下的上界进行进一步细化,并得到了一个更便于计算的上界公式。

2 一类混合态测量诱导的非双局域关联上界的优化

对于(3)式中假定的一类局域量子态ρBC=ρB⊗ρC,即其中ρB是非简并且有谱投影{|eB〉〈eB|},而ρC是简并的情况,文献[32]给出了态ρAB⊗ρCD测量诱导的非双局域关联上界。接下来,应用文献[20]中的方法对这类态的上界进行优化。

(4)

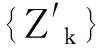
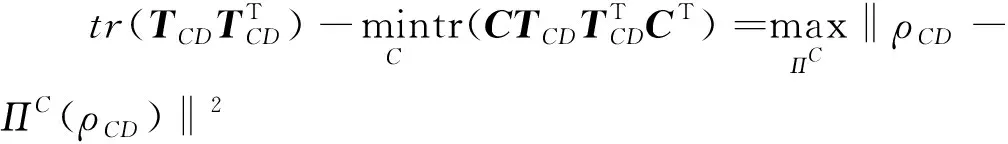
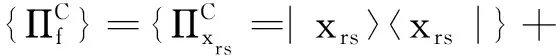
在施加保持ρC不变的冯诺依曼测量ΠC之后,态ρCD变为

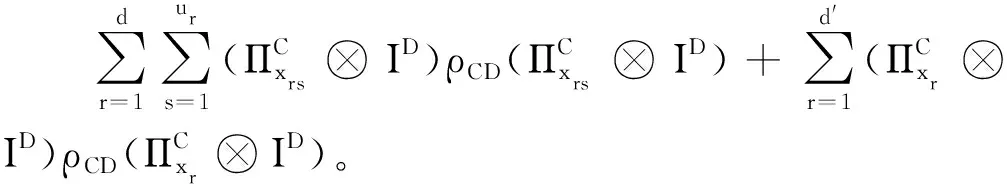
运用等式(4),有

（1）对PM2.5检测传感器进行调试，对其实际响应声光提示进行记录，烟雾采集数据、声光提示记录如表1所示。

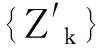
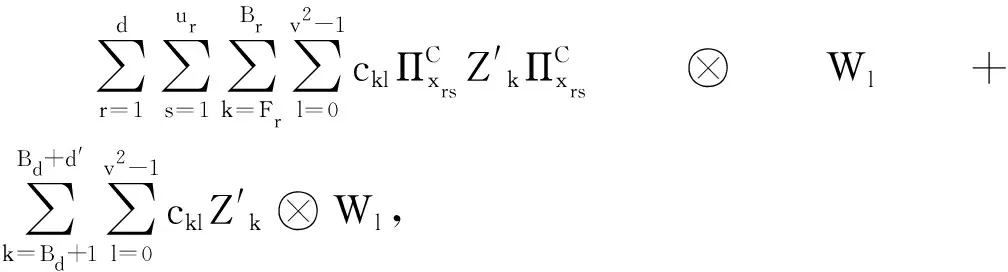
经计算,

另一方面由等式(4)和在冯诺依曼测量下ρC的不变性可知

故

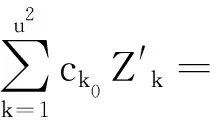
移项可得

(5)

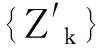
所以,等式(5)中k=Fr或k′=Fr时的项为0,且可最终写为

(6)

(7)

根据文献[32],可从等式(7)中得出一个上界,即

(8)

于是,对于(3)式可以得到一个上界计算公式

NC(ρAB⊗ρCD)=

(9)

由于这个上界可在每个简并特征子空间下独立计算得出,所以减少了以前上界(在整个空间下计算)的计算量,优化了最终的结果。

3 结语

测量诱导的非双局域关联通过测量的方式,对量子Swapping实验中的非局域性进行了有效捕获。本文针对一类量子态,即边缘态ρBC,这个直积态ρBC=ρB⊗ρC中ρB是非简并且有谱投影{|eB〉〈eB|}},和ρC是简并的情况进行了重新计算。通过重新构造局域态ρC的厄米算子基,获得了一种新的计算方法,并给出了一个更优化且更便于计算的上界公式。进一步需要研究的课题是,如何获得最一般量子态的上界计算公式。