极小最大量子态区分

张文海，张梦迪

（淮南师范学院 电子工程学院，安徽 淮南 232038）

极小最大量子态区分

张文海，张梦迪

（淮南师范学院 电子工程学院，安徽 淮南 232038）

得到在未知先验概率的情况下，区分三个非正交量子态的最优概率，给出了求解这类问题的公式，同时，把这类区分和Bayesian非正交量子态的区分相比较。该方法可以推广到N个非正交量子态问题的区分。

量子态区分；POVM测量；确定性区分；极小最大区分

量子力学的叠加原理指出，量子态可以是正交本征量子态的概率叠加。这也说明在量子态中，既有正交的量子态，也有非正交量子态的存在。由于量子不可克隆定理的限制［1］，正交的量子态可以被精确地测量，而非正交的量子态则不可能精确地测量。在量子信息科学中，量子密码术［2］就是使用非正交量子态作为量子编码，这样，窃听者就不可能精确的复制通信双方的信息。非正交量子态区分理论［3-4］为量子密码术的安全性提供理论支撑，是量子密码术理论研究的核心，同时，也揭示了认识量子世界的限度。

由于不可能被精确地测量，非正交量子态的测量方式可能会出现两种。第一，可能量子测量会出错误，但测量着希望出错误的概率最小（Minimum Error Discrimination，MED）。第二，在测量中不允许出现错误，但有时可能测量不到所需要的结果，但是，一旦测量到结果，则测量结果是明确的 （OptimalUnambiguousdiscrimination，OUD）。假设具有输入先验概率p1和p2=1-p1的两个非正交量子态，量子系统可以表示为（其中是量子系统的密度矩阵），根据量子力学量子系统的保迹性，可以有（其中Tr是求迹算符运算）。利用广义量子测量（Generalized Measurements）或称正定算符值测量（Positive-Operator-Valued Measures，POVM）［5-7］，可以在理论上给出 MED和OUD的测量结果的最优值。对MED测量，定义POVM元M^i满足完全性关系（其中为单位算符）。当测量到时可以认为输入态是，因此MED测量可以表示为

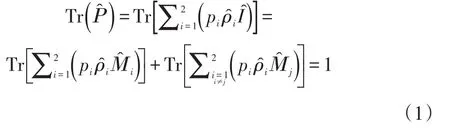
能够正确判断测量结果的概率为

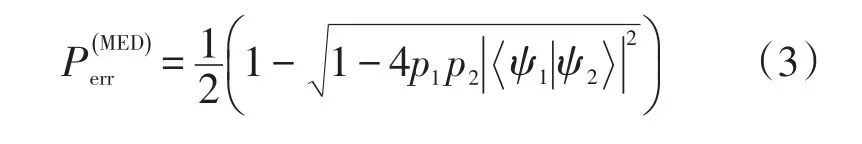
由于不允许出现错误，当测量到O^i时输入态一定是，这要求。当测量到时，不能判断输入态。因此，能够正确判断测量结果的概率为

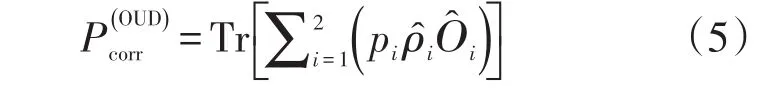
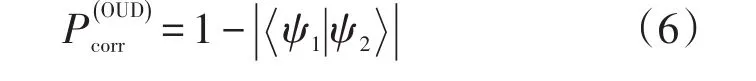
利用POVM测量，可以得到（3）和（6）式，同时也给出POVM元M^i和O^i的具体形式。然而，由于M^i和O^i都是非正交算符，在物理实验中不可能直接实现，因而不能直接验证理论的正确性。

一般情况下，输入量子态的先验概率是已知的，因此，以上所述的OUD和MED测量方案都可以称为Bayesian（贝叶斯）非正交量子态的区分。本文研究在未知先验概率的情况下，区分三个非正交量子态的最优概率（MUD），主要研究确定性区分。我们首先确定三个非正交量子态的一般形式，然后利用可以在物理系统中可以直接实现的幺正变换，给出了求解这类问题的公式，同时，把这类区分和Bayesian（贝叶斯）非正交量子态的区分相互比较。我们的方法可以推广到N个非正交量子态这类问题的区分。

1　区分两个非量子态的测量

假设具有输入先验概率p1和 p2=1-p1的两个非正交量子态，可以不是一般性的令两个非正交量子态的内积为，其中s∈（>0，1）和。我们首先让输入量子态经过一个幺正变换，可以表示为

下面我们求成功概率的最大值。

从（7）式可以得到幺正变换的内积为

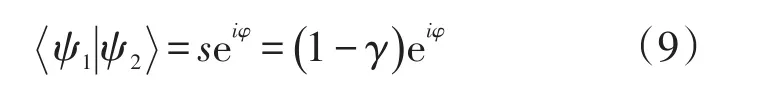
显然，从（9）式，可以直接得到最优测量概率为

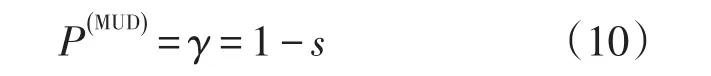
这可以和由（6）式的OUD测量作为比较，两种测量方式得到的概率是一样的，只是OUD的条件是先验概率为p1=p2=1/ 2。下面我们求解三个非正交量子态的测量。

2　三个非正交量子态的测量

假设具有先验概率 p1，p2和 p3的三个输入非正交量子态，三个先验概率满足p1+p2+p2=1。我们研究确定性区分，因此，三个非正交量子态必须是线性无关的［3］。区分可以是一般性的，令三个非正交量子态的内积为，其中sij∈（）0，1和。类似于两个非正交量子态的测量，我们设幺正变换为

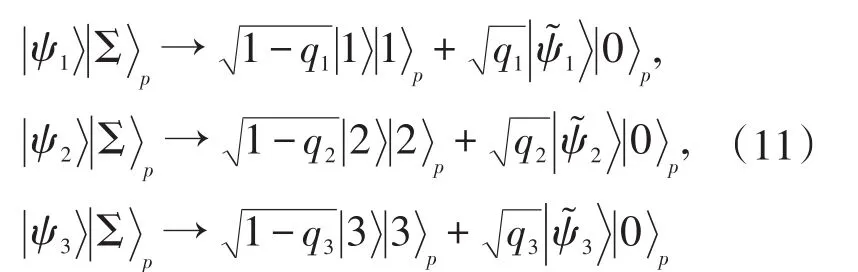
下面我们来求失败概率的最小值。从（11）式可以得到量子态的内积为

失败态必须是线性相关的。反之，如果是线性无关的，可以再进行下一个幺正变换，直至失败态线性无关为止。同时，可以设失败态满足

这样，得到求解BUD的问题为在条件下，求Q（）BUD的最小值。

我们给出幺正变换的（14）式，也是给出可以直接测量的POVM。

在未知先验概率时，这就意味着失败概率不依赖先验概率。因此，可以令qi=q≠1。在简化条件后，可以给出Max（）sij＜q＜1的条件。所以，求解条件为 在条件下， 求Q（）MUD的最小值。

对于BUD和MED，它们有不同的标准，这就导致它们有不同的约束条件，（15）和（16）式就是它们的约束条件。例如，对于BUD，条件可以是qk＞sij，但对于MED，条件必须是q＞Max（）sij。同时，对于BUD，可以存在某个失败概率是qk=1，这量子态不能被区分；但对于MUD，失败概率条件q＜1保证所有的输入量子态一定能被区分。下面，我们来比较这两种区分。

3BUD和MUD的比较

对于BUD，从条件Δ~（）BUD=0可得，失败态的行列式为：

其中 α=φ12+φ23+φ31称为 Berry相。现在考虑MUD，利用（16）式，经过计算后可得到解析式

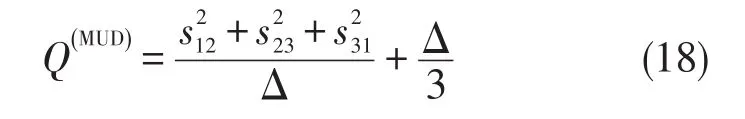
其中

现在对BUD和MUD做一个比较。假设三个非正交线性无关的量子态内积为 s23=0.5，s31=0.3和0≤s12≤0.976，并且cosα=1，先验概率相同 pi=1/3。在 0＜s12≤0.187 5区域内，有qi＜1，则解为；在区域0.187 5≤s12≤0.6，有qi＜1，则解为；在区域内，

图1给出BUD和MUD的比较，其中MUD意味着的解可以直接从（18）式中得到。

图1　BUD和MUD的比较，其中s23=0.5，s31=0.3和0≤s12≤0.976，并且cos α=1

图2　以cosα为参数的

对于N≥4的情况，即：确定性区分N个线性无关的非正交量子态，我们提供的方法仍然有效。假设以先验概率pi（且满足给出N个线性无关的非正交量子态，其内积为，则幺正变换为

其中失败态满足

4　结论

本文研究在未知先验概率的情况下，研究确定性量子区分。首先研究了两个非正交量子态的区分，然后推广到三个线性无关的非正交量子态的区分。同时，我们将BUD和MUD的两种结果作了比较。同时，我们提供的方法可以推广到对N个线性无关的非正交量子态的确定性分。

［1］ Wootters W K，Zurek W H.A single quantum cannot be cloned［J］.Nature（London）1982，299：802-803.

［2］ Gisin N，Ribordy G，Tittel W，et al.Quantum cryptography［J］，Reviews of Modern Physics，2002，4：145-195.

［3］Chefles A.Quantum state discrimination［J］.Contemporary Physics，2000，41，401

［4］ Barnett S M，Croke S.Quantum state discrimination ［J］.Advances in Optics and Photonics，2009，1：238

［5］ Kraus K.States，Effects and Operations［M］.Number 190 in Lecture Notes in Physics，Springer，Berlin，1983.

［6］ Peres P.Quantum theory：concepts and methods［M］. Kluwer，1993.

［7］ Busch P，Grabowski M，Lahti P.Operational quantum physics［M］.Springer，1995.

［8］Helstrom C W.Quantum detection and estimation theory［J］.Journal of Statistical Physics，1969，1（2）：231-252.

［9］ ⅠvanovicⅠD.How to differentiate between non-orthogonal states［J］.Physics Letters A，1987，123（6）：257-259.

［10］Dieks D.Overlap and distinguishability of quantum states［J］.Physics LettersA，1988，126（5/6）：303-306.

［11］Peres A.How to differentiate between non-orthogonal states［J］.Physics LettersA，1988，128（1/2）：19.

Minimax quantum state discrimination

ZHANG Wen-Hai，ZHANG Meng-Di

（School of Electronic Engineering，Huainan Normal University，Huainan Anhui，232038，China）

We derive the optimal probabilities for minimax unambiguous discrimination（MUD）among three pure states without knowing a priori probabilities.We present the formulation for solving the MUD problem，and make a detailed comparison between MUD and Bayesian unambiguous discrimination（BUD）with a priori probabilities when N=3.Our method can be generalized to any N linearly independent pure states.

quantum state discrimination；POVM measurement；unambiguous discrimination；Minimax unambiguous discrimination

O0413

A

1004-4329（2016）01-027-04

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）01-027-04

2015-10-11

淮南师范学院2015年“支持百名优秀学生课外科技实践创新活动基金”项目（2015XS157）资助。

张文海（1968-），男，博士，副教授，研究方向：量子信息。