自适应图正则化稀疏编码算法

余沁茹,卢桂馥,李 华

(1 芜湖职业技术学院, 安徽 芜湖 241000; 2 安徽工程大学 计算机与信息学院,安徽 芜湖 241009)

在图像处理过程中,图像本身的表示形式是影响处理结果的关键因素。稀疏表示已被证明是一种极有效的图像表示算法[1]。近年来,为了实现稀疏表示,研究人员已经开发出例如稀疏主成分分析(PCA)[2]、稀疏非负矩阵分解(NMF)[3]等多种算法。作为稀疏表示最典型的方法之一,稀疏编码(spares coding,SC)在机器学习、信号处理和神经科学[4-7]等领域中得到了广泛的关注。

SC是利用过完备字典来线性表示图像的编码过程,其中的非零元素只占所有元素的极小部分,体现了编码的稀疏性。SC具有众多优点,如:稀疏表示时其每个数据点都表示为少量基本矢量的线性组合,表示方式更简洁;编码状的稀疏表示可以允许数据快速检索等。SC算法目前已被应用于如图像恢复[8]、信号分类[9]、人脸识别[10]和图像分类[11-12]等多个领域中。

近年来,研究人员针对SC的部分缺点提出了改进算法。对于SC计算复杂度过高的问题,文献[10]提出了一种迭代的软阈值方法,该方法在负梯度方向上取Barzilai-Borwein步长,然后将软阈值算子应用于结果,提升了SC的计算速率。 Lee等[13]提出了一种特征符号搜索方法,将不可微L1范数问题简化为L1正则化最小二乘问题,从而加快了优化过程。在传统方法中,SC的字典选择也是影响算法效果的一个关键因素,然而其字典一般是从标准库中选择的[14],甚至是从随机矩阵[15]中生成的。因此,有些学者试图通过为稀疏编码设计一个更合适的字典来提升SC的性能。Aharon 等[16]提出的K-SVD方法不同于之前利用标准库获得数据稀疏表示的算法,该算法使用正交匹配追踪算法(orthogonal matching pursuit, OMP)或基追踪算法(basis pursuit, BP),作为其学习词典迭代过程的一部分。还有些学者致力于将稀疏编码与经典机器学习方法相结合以提出新的理论框架。文献[17]将线性判别分析(linear discriminant analysis, LDA)与稀疏表示相结合提出了稀疏主成分判别分析的方法(sparse linear discriminant analysis,SDA),该方法可以通过重建特性、辨别力和稀疏性来进行分类。文献[11]提出了一种新的判别方法,称为监督字典学习算法(supervised dictionary learning,SDL),有效地利用图像分类任务中相应的稀疏信号分解去学习共享字典和判别模型。

以上研究都在克服原始稀疏编码的不同缺点,但是都没有考虑到数据中潜在的几何结构。Kavukcuoglu等[18]提出了几种稀疏编码方法的变体,这些算法通过增加一些稀疏编码系数的附加约束来捕获数据中的结构,即它们可以通过添加额外的空间一致约束来学习,以获得局部不变的稀疏表示。Gao等[19]首次提出了使用流形学习算法学习数据几何结构的方法,但未明确提出详细的优化方案,所提方法的性能仅在图像分类任务上进行了评估。Zheng等[20]在文献[19]的基础上提出了一种新的算法,称为图正则化稀疏编码(graph regularization sparse coding,GraphSC),该算法明确考虑了数据的局部几何结构。 GraphSC通过构建一个近邻图来编码数据中的几何信息,并使用谱图理论中的图拉普拉斯算子作为光滑算子来保留局部流形结构。与传统的SC算法相比,GraphSC具有更强大的分类能力。基于文献[20]的研究,Gao等[21]基于直方图交点的度构建相似度图,利用超图捕获样本之间的高阶关系,进一步提升了GraphSC的性能。此后,Sha等[22]提出将低秩表示[23](low-rank representation, LRR)引入图正则化的处理过程,并就此提出了低秩正则化稀疏编码算法(low-rank regularized spares coding,LogSC)。由于添加了低秩约束,LogSC在部分任务中获得了较GraphSC更优秀的性能。

然而,GraphSC及其改进方法中的拉普拉斯图都是预先定义且固定不变的,并不会参与之后对于字典与稀疏编码的学习过程,而预先定义的拉普拉斯图往往不是最合适的。针对这个问题,我们对GraphSC算法进行了改进,提出了自适应正则化稀疏编码(graph regularization sparse coding with adaptive neighbour,GraphSCAN)算法。我们假设数据指向较小的距离代表更可能成为邻居,因此 GraphSCAN可以从自适应性分解的结果中学习局部流形结构,并重新构造以保留精炼的局部结构,根据每个数据点的本地连通性选择自适应近邻(adaptive neighbor, AN)以获得相似度图,然后将ANs正则化约束合并到GraphSC中。GraphSCAN将图的构建和稀疏编码纳入到统一框架中,使得内部局部结构学习的过程和图稀疏编码的过程同时进行,并最终提高了GraphSC的性能。

1 相关工作

1.1 稀疏编码(SC)

SC的目的是对于给定的一个数据矩阵,找到一组捕获高级语义的基础向量(即字典),并输出数据的稀疏表示。

给定一个数据矩阵X∈[x1,x2,…,xn]∈Rn×m,X的每一列都是样本矢量。令A=[a1,a2,…,ak]∈Rn×k为字典矩阵,其中ai表示字典中的基础向量。令E=[e1,e2,…,em]∈Rk×m为系数矩阵,其中每一列都是数据点的稀疏表示。每个数据点都可以表示为字典中基向量的稀疏线性组合。

稀疏编码的目标函数定义如下:

(1)

式中:‖‖F表示矩阵的F范数;f是度量的稀疏性函数,其最直接的选择是e的L0范数。然而,当固定字典B时,系数e的极小化问题被证明是一个NP困难问题[24]。因此,可以转而讨论这个问题的近似或松弛。近似求解该问题有2种常用的方法,即匹配追踪(matching pursuit,MP)[25]和基追踪(basis pursuit, BP)[26]。MP以贪心的方式一次只寻找一个条目的解,而BP用L1范数代替L0范数对原问题进行凸松弛。

因此,由文献[13,26-27],可令f为f(ei)=‖ei‖1,此时目标函数化为

(2)

由于(2)式中的目标函数可能仅A或E是凸的,2个变量不能同时为凸。因此,可以通过固定一个变量、最小化另一个变量来迭代优化目标函数(2)。

1.2 图正则化稀疏编码(GraphSC)

GraphSC将拉普拉斯图引入SC算法,并使用图拉普拉斯正则项来保留数据局部流形结构。

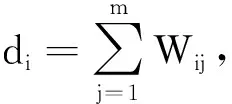
图正则化目标函数[20]可表示为

(3)

式中L是图拉普拉斯矩阵,L=D-S。由(2)、(3)式可得GraphSC的目标函数为

(4)

2 自适应图正则化稀疏编码算法及其求解

利用数据的局部几何结构,GraphSC算法提升了SC算法的计算能力。但GraphSC使用的拉普拉斯图会在全局计算前预先定义且固定不变,并不参与之后对于字典与稀疏编码的学习过程。我们提出自适应方图正则化稀疏编码的算法(graph regularization sparse coding with adaptive neighbour,GraphSCAN)对GraphSC所存在的这个问题进行了改进。

2.1 GraphSCAN的算法模型

设输入的原始数据集为X,X中的任意一数据点xi都有所有数据点{x1,x2,…,xn}可以作为近邻与之连接,连接的概率为sij。基于数据点间的欧几里得距离构造邻域矩阵,距离越小则成为最近邻的可能性越大。本文算法的求解形式如下:

(5)

(5)式第1项对原始数据集X求其字典及其稀疏编码,其中矩阵X为原始数据集,A代表字典阵,E代表其稀疏阵。

(6)

式中γ是正则化参数。因此,可以将(6)式重新表示为

(7)

通过求解(7)式获得的矩阵S∈Rn×n,可被视为相似度矩阵[29-30]。 可通过以下步骤来表示数据平滑度:

tr(ETDSE)-tr(ETWSE)=

tr(ETLSE)。

(8)

(5)式第3项是度量第一项中稀疏矩阵E稀疏度的函数,设f(ei)=‖ei‖1作为度量函数。

(5)式第4项是局部图拉普拉斯约束函数,使用其增强传统低秩表示模型的局部性和稀疏性。其中LS是Si的拉普拉斯矩阵,LS=DS-WS,tr( )表示矩阵的迹。

2.2 GraphSCAN的算法求解

本节提出求解GraphSCAN的更新算法,该算法通过固定其他变量更新一个变量的值来优化目标,此过程重复直到收敛。

2.2.1 固定A、E更新S

观察(5)式不难发现,在固定A、E时更新S,最小化(5)式可等价于解决下式:

(9)

(10)

可通过逐个求解的方式求解(10)式,此时(10)式等价于

(11)

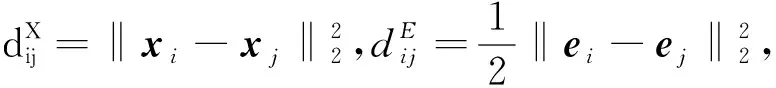
(12)

设ζ和η≥0为拉格朗日乘子,则(12)式的拉格朗日函数为

(13)

根据KKT条件[31],满足sij≥0,最优解可以定义为

(14)

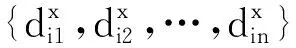
(15)

(16)

结合(15)和(16)式,可得

(17)

为了获得具有k个非零值的最优si,可以将γi设置为

(18)

为了便于计算,可以将整体γ设置为γ1,γ2,…,γn的均值,即

(19)

通过取γi的平均值,所有si的平均非零元素应为k。我们不直接搜索正则化参数γ,而是搜索近邻数k。因为k是一个整数,并且其值是有限的(即0≤k≤n),所以参数搜索会更加容易。

2.2.2 固定S、A更新E

在固定S、A时更新E,求解(5)式即等同于求解下式:

λtr(ETLSE)。

(20)

(21)

拉普拉斯正则项tr(ETLSE)可写为

(22)

结合(21)、(22)式可重写如下:

(23)

在更新ei时,其他向量{ej}j=1是固定的,因此可得

(24)

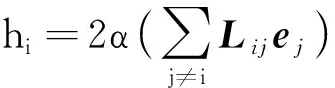
定义

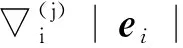
(25)

(26)

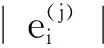
2.2.3 固定S、E更新A

在固定S、E时更新A,最小化(4)等同于求解下式:

s.t.‖ai‖2≤c,i=1,2,…k。

(29)

使用拉格朗日对偶法对(29)式进行求解。令ε=[ε1,ε2,…,εk]为与不等式约束相关联的拉格朗日乘数,则拉格朗日对偶函数为

g(ε)=infBL(A,ε)=

(30)

令Λ为k×k的对角矩阵,其对角线数Λii=λi。那么L(A,ε)可写作

tr(ATAΛ)-ctr(Λ)=

tr(XTX)-2tr(ATAΛ)+tr(ETATAE)+

tr(ATAΛ)-ctr(Λ)。

(31)

令(31)式的一阶导数等于零即可获得最佳解A*,即

A*EET-XET+A*Λ=0。

(32)

这时,有

A*=XET(EET+Λ)-1。

(33)

将(33)式代入(31)式可得

g(ε)=tr(XTX)-2tr(XET(EET+Λ)-1EXT)-

ctr(Λ)+tr((EET+Λ)-1EXTXET)=

tr(XTX)-tr(XET(EET+Λ)-1EXT)-

ctr(Λ)。

(34)

由此可得拉格朗日对偶函数

s.t.εi≥0,i=1,2,…,k。

(35)

(35)式可以通过牛顿法或共轭梯度来求解。令Λ*为最优解,那么最优A*=XET(EET+Λ)-1。由于不能保证EET+Λ可逆,因此本文算法使用伪逆代替直接求逆。

至此,GraphSCAN的算法步骤可总结如下。

3 实验

我们在2个图像数据集(CMU-PIE数据库和COIL20图像数据库)上进行聚类实验。实验中以聚类准确率(accuracy, ACC)、标准互信息率(normalized mutual info, NMI)2个指标作为评价标准,实验环境为Intel(R) Core(TM) i7-1065G7 1.50 GHz CPU,16 GiB DDR3内存,MATLAB 2019b。

3.1 实验步骤

为了进一步评估所提出方法的性能,我们对GraphSCAN与一些经典算法和最新算法进行了对比实验。

1)k-means:最常用的基于欧式距离的聚类算法[32]。

2)主成分分析(principal component analysis,PCA):经典的降维方法[33]。

3)SC:经典SC算法 。

4)GraphSC:图正则化的SC[20]。

5)LogSC:最新的基于拉普拉斯图正则化的SC[22]。

实验中所用对比算法的参数已结合原论文进行了调节,使得其性能达到最优。

3.2 图像聚类实验

3.2.1 CMU-PIE数据集上的测试

我们首先在CMU-PIE数据集上进行实验, CMU-PIE人脸数据库包含68个人总共41 368张人脸图像。每个图像的大小为32×32,每个像素256个灰度级,每个图像都由1 024维矢量表示。

我们进行的聚类实验的簇数C范围为4～68。对于除68以外的每个簇,对不同随机选择的簇进行20次测试运行,并通过对20个测试取平均值来获得最终的性能得分。对于每个测试,首先应用比较算法中的每个算法,学习数据的新表示形式,然后在新的表示空间中应用k-means。我们用不同的初始化将k-means在原数据集上重复50次,并记录关于k-means目标函数的最佳结果。PCA投影降维后,维数为64。对于SC、GraphSC、LogSC、GraphSCAN算法,基向量维度设为128。

实验结果如表1所示,本文GraphSCAN算法基本优于其他算法(表中加粗数据)。GraphSCAN的ACC和NMI均值分别为86.28%和94. 41%,明显高于现有优秀算法LogSC在PIE数据集上的表现。同时,基于图的SC算法结果均优于标准SC算法。这说明结合图的SC可以获得更好的性能,且通过自适应邻居获得相似度图的方法比仅使用k-NN进行构造的图算法获得的结果精度更高。由于局部流形结构的学习和稀疏编码是同时进行的,即从编码的结果中自适应地学习内在局部结构,并且重新构造因子以保留数据的精炼局部结构。因此,可以更好探索数据内在局部结构。通过为每个数据点选择自适应和最佳邻居,该方法可以提高一般情况下的聚类性能。

表1 CMU-PIE数据集的聚类结果Tab.1 Clustering results of CMU-PIE data set 单位:%

3.2.2 COIL20数据集上的测试

我们在COIL20数据集上也进行了实验, COIL20图像库包含20个对象1 440张32×32的灰度图像(每个对象72个图像),每个图像由1 024维向量表示。实验设置与CMU-PIE数据集上的实验基本相同,但限制于数据集大小,此处以2～20的簇数进行20次实验,通过对20个测试取平均值来获得最终的性能得分。对于此数据集,PCA降维后的维数为175;对于SC、GraphSC、GraphSCAN算法,基向量维度设为256。

实验结果如表2所示,GraphSCAN的ACC和NMI均值分别为88.07%和87.63%。与LogSC相比,GraphSCAN的性能略有提升,且二者都优于同样基于图的GraphSC算法。这说明将图优化的概念引入使用图方法的GraphSC中,可以提高原有算法的性能。

表2 COIL20数据集的聚类结果Tab.2 Clustering results of COIL20 data set

结合对PIE数据集进行的聚类实验结果可以看出,通过将自适应拉普拉斯图构建的概念引入带有几何信息编码的稀疏表示中,可以有效提高学习性能。

3.3 参数选择实验

观察目标函数(5)可以看出,GraphSCAN中包含了α、β、λ3个参数。根据文献[20,28]中实验不难发现,虽然α、β取值会影响实验结果,但是由于其取值范围较小,且因其改变而影响的实验结果误差不大,故此处仅讨论对算法中参数取值范围及实验结果影响较大的参数λ的选择。

考虑到实验数据集包含的数据量,这里选择COIL20以及CEU-PIE 2个数据集及PCA、SC、GraphSC、GraphSCAN 4种算法进行了实验。所有实验均使用ACC、NMI指标作为算法评价标准。为了公平地比较所有方法,所有算法都在不同的参数设置下进行,且在每个参数设置下,均会独立重复实验20次。所有方法的迭代次数都根据经验设置为50,GraphSCAN中α、β两个参数粗略取值为α=λ、β=0.3进行实验(更好的参数调整可以给本文算法带来更优秀的性能)。聚类的数量设置为真实类的数量。

试验结果如图1所示。可以看出,在CEU-PIE数据集上当λ取到0.1时以及在COIL20数据集上当λ取到1时可获得较好的结果,其结果显示GraphSCAN与GraphSC算法取到λ最优值过程中指标变化趋势相差较小。以上结果表明,实际对算法影响较大的部分为SC之前进行的图构造过程。

图1 各算法中参数λ对性能的影响Fig.1 The influence of parameter λ on different algorithms

4 结语

为优化GraphSC算法,本文将自适应拉普拉斯图构建的方法引入GraphSC中,提出了自适应图正则化稀疏编码算法GraphSCAN。该算法通过使用自适应方法定义构建合适的局部拉普拉斯图,再使用构建好的图参与SC的运算,图的构建与稀疏编码的运算同时迭代进行。本文在2个图像数据集上进行了实验,并与相关算法进行了比较分析,验证了GraphSCAN的有效性。