信息谱熵的链式关系

王晨旸, 席政军

(陕西师范大学 计算机科学学院, 陕西 西安 710119)

Shannon提出了简单的离散无记忆信源和信道模型,考虑独立同分布的(independently and identically distributed, i.i.d.)随机变量,采用渐近均分性(asymptotic equipartition property, AEP)给出了可靠通信的充要条件[1];但现实的信息处理过程中,常见的信源和信道是非平稳或有记忆的,Shannon信息论方案并不能直接应用。Han等[2-4]提出信息谱方法(information-spectrum methods)构建了更一般的编码框架,分析非平稳信源的数据压缩或离散有记忆信道的信道编码等问题。Han[4-5]等也运用信息谱思想给出了大偏差概率理论中的假设检验问题,并通过谱散度率给出一般信源(包括非平稳或非遍历信源)第二类误差概率的最佳指数。信息谱方法还应用于通信理论的其他领域,如一般的Gelfand-Pinsker信道的容量问题[6]以及随机数的萃取[7]。文献[8-10]将非独立同分布随机序列假设检验的方法运用到一般量子态序列的假设检验问题。Hayashi和Datta[11-12]各自用不同的方式将谱散度率推广到量子情形中,称之为量子谱散度率。量子谱散度率在量子纠缠度量和平滑熵中有很好的应用[13-14]。量子信息谱在经典-量子信道容量[11]、量子信源编码[15]、带限制边信息的经典-量子信道编码[16]、有限码长的二阶情形[17]等方面应用广泛。

无论是经典还是量子情形下的信息谱方法,均为码长n充分大时的渐近情形。当n充分大时,在实际中由于设备等限制,不可能达到理论预期,必然产生误差。因此,有必要考虑非渐近的情形,即有限码长或者有限次信道使用。在one-shot信息论框架中,一次只使用单一的信源或信道,在允许容忍误差的条件下,讨论信源压缩和信道编码。one-shot情形下的Tomamichel等[18]给出了信息谱相对熵(information-spectrum relative entropy),并给出了信息谱相对熵在i.i.d.情形下的极限形式。特别地,Anshu等[19]给出另一类谱散度率的定义,得到了它与平滑最大信息的关系,并将其应用到态的分离情形。在one-shot情形下,信息谱方法也应用于随机数萃取[18,20]以及具有量子边信息的信源压缩的可达界[21]研究。

信息谱相对熵的本质是概率分布的对数似然比,而相对熵是对数似然比的期望,且用Shannon熵定义的信息度量都完全可以由相对熵来刻画。受此启发,本文考虑用信息谱相对熵来定义信息谱条件熵和信息谱互信息。在Shannon熵的理论框架中,由于Bayes规则,条件熵的链式法则(chain rules)[22]在信源编码和信道编码中有非常重要的应用。目前,关于信息谱应用的研究相对较多,而对于信息谱相对熵本身的研究相对少且不完整,并且没有得到系统的讨论。因此,本文首先给出one-shot情形下的信息谱相对熵定义,并详细讨论了其性质。特别地,讨论信息谱相对熵与假设检验相对熵的关系。研究表明,在误差容忍的情况下,这两个量化是等价的。基于信息谱相对熵刻画了信息谱条件熵和信息谱互信息,得到了一些有意义的性质。由于信息谱互信息存在不同的定义方式,本文重点讨论了不同定义互信息之间的关系,进而给出了它们的链式关系。

1 信息谱相对熵

在Shannon信息论框架中,很多结果都依赖于渐近均分性。若随机变量序列X1,X2,…,Xn服从独立同分布,由大数定律可知,随机变量的函数依概率收敛于Shannon熵,即

(1)

H(X)=

(2)

(3)

和

D(PX‖QX)=

(4)

定义1给定一个概率分布PX及次归一化概率分布QX(概率分布求和小于等于1),对于ε∈[0,1],上、下信息谱相对熵分别定义为

(5)

和

(6)

上、下信息谱相对熵在随机数萃取和具有边信息的信源压缩中有很好的应用。但是,对于这2个量化,只针对具体问题给出了应用,它们本身的性质并没有得到详细研究。比如,经典信息论中,依赖相对熵可给出条件熵、互信息以及信息处理不等式等。本文将详细讨论其性质。

命题1对2个概率分布PX和QX,且ε∈[0,1],有

1)当ε′≥ε,有

(7)

(8)

2)对于常数c>0,有

(9)

(10)

3)若存在概率分布Q′≥Q,则有

(11)

(12)

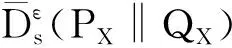
根据上信息谱相对熵的定义直接可得

根据上信息谱相对熵的定义可得

同理可得,

为了讨论one-shot情形下假设检验相对熵和信息谱相对熵之间的关系,首先给出假设检验相对熵的定义[23]。

定义2对于概率分布PX和次归一化概率分布QX,对于ε>0,假设检验相对熵定义为

(13)

下面给出信息谱相对熵近似等价于假设检验相对熵。

命题2给定概率分布PX及次归一化概率分布QX,对于δ、η>0,0<ε<1且0<δ+ε<1,则有

(14)

(15)

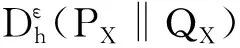
由此可推出

(16)

对于任意实数r,有

(17)

(18)

结合不等式(17)及不等式(18),可得

当ξ→0时,不等式得证。

进而有

1-ε-δ。

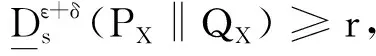
在经典信息论中,一对随机变量的两个联合分布PXY和QXY之间的相对熵可以表示为相对熵与条件相对熵的和,通常称之为相对熵的链式关系[22],即

D(PXY‖QXY)=

D(PX‖QX)+D(PY|X‖QY|X),

(19)

其中D(PY|X‖QY|X)是条件相对熵,且

D(PY|X‖QY|X)=

QY|X(y|X=x))。

(20)

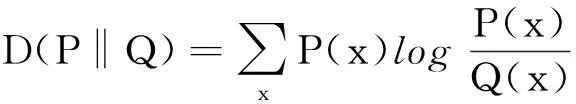
定义3给定条件概率分布PY|X和QY|X,对于ε∈[0,1],上、下信息谱条件相对熵定义为

(21)

(22)

由于涉及极限和参数不等式,上、下信息谱条件相对熵并不具有像条件相对熵一样的链式关系,只能给出一个类似的情形,下面给出信息谱相对熵的链式关系。

命题32个联合分布PXY和QXY,对于0<ε1+ε2≤1,有

(23)

(24)

式中ε=ε1+ε2。

显然,对(x,y)∈S1∪S2,有PXY(x,y)≥2a1+a2QXY(x,y)。因此,可得

2 信息谱条件熵和互信息

在Shannon信息论中,Shannon熵、条件熵以及互信息都可以由相对熵表示。结合前面的讨论,本节将考虑使用信息谱相对熵来刻画one-shot情形下的条件熵和互信息,并给出相应的性质。

定义4给定概率分布PX,对于ε∈(0,1),上、下信息谱熵分别定义为

(25)

(26)

式中1X(x)=1,∀x∈X。

显然,这里上信息谱熵和下信息谱熵也是上谱熵率(1)和下谱熵率(2)在one-shot情形下的形式。下面给出one-shot情形的条件熵。

定义5给定联合概率分布PXY,以及相应的边际概率分布PY,对于ε∈[0,1],上、下信息谱条件熵分别定义为

(27)

(28)

由于条件Bayes概率,在Shannon信息论中,有

H(X|Y)=H(XY)-H(Y)。

(29)

该等式也称为熵的链式法则。结合定义以及概率不等式,下面给出信息谱条件熵的链式关系。

命题4对于联合概率分布PXY,及边际概率分布PY,若0<ε1+ε2≤1,则

(30)

式中ε=ε1+ε2。

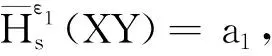
ε1+ε2。

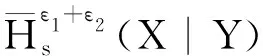
类似上信息谱条件熵,容易得到下信息谱条件熵的链式关系。

命题5对于联合概率分布PXY及边际概率分布PY,若0<ε1+ε2≤1, 有

(31)

式中ε=ε1+ε2。

由于涉及参数与概率不等式,一般情况下很难得到等号成立的关系,目前得到的结果有助于理解不同信息谱熵之间的关系,并期望能在具体信息处理尤其是one-shot情形下的随机数萃、信道编码以及多址接入信道中得到应用。最后,考虑与相对熵相关联的另一个重要量化——互信息。

定义6给定联合概率分布PXY和相应的边际概率分布PX,对于ε∈[0,1],则上、下信息谱互信息分别定义为

(32)

(33)

由于信息谱相对熵是非负的,显然,易知信息谱互信息也非负。Shannon相对熵是一个信息距离度量,从而互信息可以看做是给定联合分布到不同乘积分布集合上的最小相对熵。结合相对熵的性质,可以给出互信息的4种等价定义。但是,这种描述在广义熵中并不存在等价定义,比如Renyi相对熵以及量子版本的各类Renyi相对熵。最后,利用信息谱相对熵来讨论互信息的不同定义并建立它们的关系。

定义7给定联合概率分布PXY、边际分布PX以及次归一化概率分布QX和QY,对于ε∈[0,1],信息谱互信息可定义为

(34)

(35)

(36)

(37)

注意,这里并没有考虑关于随机变量X的最小化定义,显然它们的定义及相关性质与随机变量Y的情形类似。同时,如果最小化在联合概率分布的边际概率上可达,就类似于常见的Shannon互信息。下面给出上述4类互信息的序关系。

命题6给定联合概率分布PXY、边际分布PX以及次归一化概率分布QX和QY,对于0<ε+δ≤ε+δ+η<1,有

(38)

(39)

∀(x,y)∈S1∪S2有

可得

对于(x,y)∈S3∪S4,有

该结果说明,由于取优化不同而导致的不同互信息,它们之间依赖于某个参数。在给定参数下,可以看做它们是等价的。有了信息谱熵、信息谱条件熵以及信息谱互信息,自然地可以给出类似于Shannon熵、条件熵以及互信息之间的关系,即

I(X:Y)=H(X)-H(X|Y)。

(40)

结合命题4和命题5的证明过程,对于0<ε1+ε2≤1,有

(41)

式中ε=ε1+ε2。

3 结语

信息谱方法不仅拓展了Shannon信息论和量子信息论的研究领域,而且为信息处理提供了新的理论框架。本文研究了信息谱相对熵的性质,以及信息谱相对熵与假设检验相对熵的关系。特别地,建立了信息谱相对熵的链式关系。基于信息谱相对熵定义了信息谱条件熵和信息谱互信息,分别给出了它们之间的链式关系。信息谱互信息并不同于Shannon互信息的单一形式,它存在不同的定义方式,本文也得到了不同信息谱互信息之间的等价关系。随着量子信息技术的发展,在量子信息处理中也会遇到非独立同分布的情形,但是由于量子态的非对易性,将经典的结论直接推广到量子情形目前还存在困难。虽然前人已经给出量子信息谱相对熵的一些应用,但本文中关于量子信息谱相对熵的链式关系至今没有解决。因此,下一步将考虑量子信息谱相对熵的链式关系。