基于知识图谱的MOOC课程推荐
2023-09-13曹小兰张怡文单春宇
曹小兰,张怡文,单春宇,张 力
(1.安徽建筑大学 电子信息与工程学院,安徽 合肥 230601;2.安徽新华学院 信息工程学院,安徽 合肥 230088)
0 引言
在线教育平台随着互联网技术的快速发展越来越受欢迎,用户可以在海量的资源中学习,但由于学习资源的丰富多样,用户在大量的课程选择中,容易信息过载[1-2]。如何根据用户的学习情况为用户推荐课程成为研究的重点[3-4]。
在推荐领域中,推荐算法主要有基于项目的推荐[5-6]、基于内容的推荐[7]以及混合推荐[8]。目前已有研究者对推荐系统进行深入研究,在一定程度上缓解信息过载的问题,但存在一些问题。He 等[9]提出LightGCN 模型,该模型在图卷积网络的基础上,将图卷积神经网络(GCN)的特征变换和非线性激活丢弃,简化模型来预测用户对项目的分数,充分利用用户项目的高阶邻域信息,但没有利用项目之间额外的辅助信息。李宇琦等[10]根据用户项目的交互记录构建商品网络,利用用户和商品的向量表示计算用户和商品之间的相似性从而进行推荐,结果表明该算法提升推荐效果,但没有结合项目自身的属性。李君等[11]将模型设计为推荐模块、交叉压缩单元、知识图谱模块。利用交叉压缩单元来更新物品的表示,同时引入注意力机制为不同特征分配权重。将用户和物品的特征表示输入多层感知机来预测概率,结果表明该模型的推荐效果有一定提升,但只利用实体一阶邻域关系,没有加入更高阶的邻域信息。陈晋鹏等[12]将知识图谱作为物品的表示向量,利用滤波器对物品的表示向量进行卷积处理,最终与用户的表示向量进行连接来预测,但忽略物品之间的关系存在更丰富的表示。徐硕等[13]提出基于知识图谱与协同过滤的个性化试题推荐,首先建立知识点知识图谱。利用TransE学习知识点实体对向量表示,再利用余弦相似度来提取知识点的相似性,最终为用户推荐,但该算法忽略不同的项目关系对特定用户的影响不同。综合上述文献,这些方法在一定程度上提高推荐性能,但没有充分利用项目之间的语义关系。因此本文考虑结合知识图谱和图神经网络,通过训练课程实体之间的关系进行课程推荐,丰富推荐系统在教育领域的应用。
本文提出基于知识图谱的MOOC(Massive Online Open Courses)课程推荐算法,利用MOOCCube平台所有课程与知识点、所属领域、授课老师、开设大学之间的关系来构建课程知识图谱。将课程知识图谱和图神经网络进行融合,发掘用户的个性化兴趣。根据用户和课程属性选择性聚合邻域信息,丰富课程实体表示,为用户推荐更合适的课程。
1 相关研究
1.1 知识图谱
知识图谱[14]本质上是一个语义网络的知识库,简单来说,知识图谱把所有的信息连接在一起构成关系网络,主要应用于语义匹配、搜索推荐、问答对话、推理决策、区块链协作等领域,和自然语言处理(NLP)有紧密的联系。知识图谱的基本单位由三元组构成,三元组由实体、属性、关系构成。将知识图谱引入到推荐系统中,能得到较好融合异构信息的网络,并同时建立各个实体和属性之间的关系,弥补传统推荐算法的不足。
1.2 推荐系统的知识图卷积网络
推荐系统的知识图卷积网络(Knowledge Graph Convolutional Networks for Recommender Systems,KGCN)首先建立课程知识图谱,对于知识图谱中邻居实体的关系采取不同的权重,运用图神经网络计算知识图谱中给定实体的表示,聚合和合并邻域实体来学习预测函数=F(u,v|Θ,Y,G),表示用户u对课程v产生交互的可能性,Θ表示函数F的模型参数。Y表示用户交互矩阵,对于给定的用户U={u1,u2,…,um},项目V={v1,v2,…,vn},用户交互矩阵Y∈RM*N,其中yUV=1表示用户u与课程v之间存在交互,否则YUV=0,G为课程知识图谱。对于KGCN单层的描述如下。
在KGCN一阶连接中,N(v)表示与课程v相邻的实体集合;rei,ej表示实体ei与ej之间的关系;用函数g:Rd×Rd→R 表示关系对用户的重要性,其中d表示维度,如式(1)所示:
式(1)中u∈Rd,r∈Rd。得到用户对关系的兴趣度,则课程的领域线性组合表示如式(2):
式(2)中e是实体e的向量表示,是归一化之后的结果,如式(3):
由于一个实体存在邻居过多的情况,对整体模型效果存在干扰。为了减小影响,每个实体v邻域大小固定,具体实体v的邻域表示为,其中S(v)≜{e|e~N(v)},|S(v)|=K是常量,表示实体v的感受野。最终将实体表示v与其邻域表示聚合为单个向量,使用聚合器aggsum:Rd×Rd→Rd,将2个向量相加,进行线性变换。如式(4)所示:
其中W是变换权重,b是偏差,σ是非线性函数。
2 基于知识图谱的MOOC课程推荐
本文提出基于知识图谱的MOOC 课程推荐算法(Knowledge Graph Convolutional Networks for MOOC Course Recommender Systems,KGCN-MC),首先结合课程的知识点、所属领域、开设大学以及授课老师内容建立知识图谱,利用该模型获取知识图谱实体之间的邻域信息,预测用户对课程的兴趣。KGCN-MC模型整体框架如图1所示。
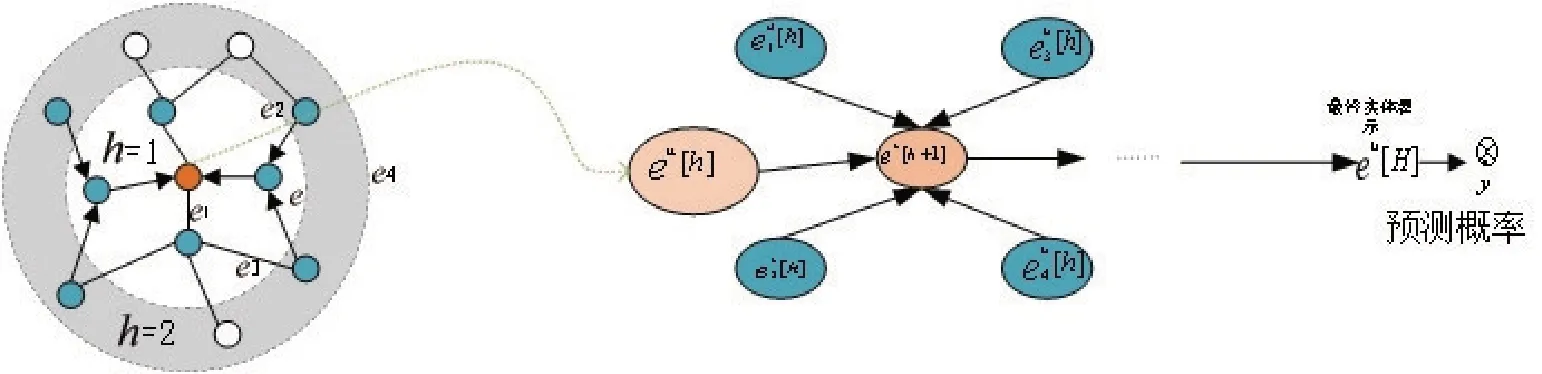
图1 KGCN-MC模型框架
2.1 数据集
数据集采用MOOCCube数据集,该数据集是由清华大学团队从学堂在线中获取课程、概念和学生的实体并根据实体间的丰富关系将数据组织成知识库的形式。教育资源数据库规模庞大,数据丰富且多样。其中的学生行为记录包括学生id、视频总时长、学习时长、学习次数、学习视频的区间等,视频观看学习将近500万人的记录。数据集预处理的具体步骤如下:
(1)从MOOCCube数据集中将每个学生观看的视频信息进行合并,统计同一门课程的视频总时长和学生观看信息。
(2)对于缺失或重复的数据,选择丢弃。
(3)将学生实际观看时长/课程总时长作为学生的学习成绩,如把学生观看时长记为t,课程总时长记为T,学生的学习成绩记为score,则score=t/T。并将学习成绩化为5个等级,其中score<0.2,得分为1;0.2≤score<0.4,得分为2;0.4≤score<0.6,得分为3;0.6≤score<0.8,得分为4;score≥0.8,得分为5。
2.2 课程知识图谱的构建
课程知识图谱采用自底向上的构建方法,从数据集中抽取课程实体、属性以及实体之间的关系,对其进行数据整合,形成标准的数据表示来建立三元组,构建知识图谱,步骤如图2所示。
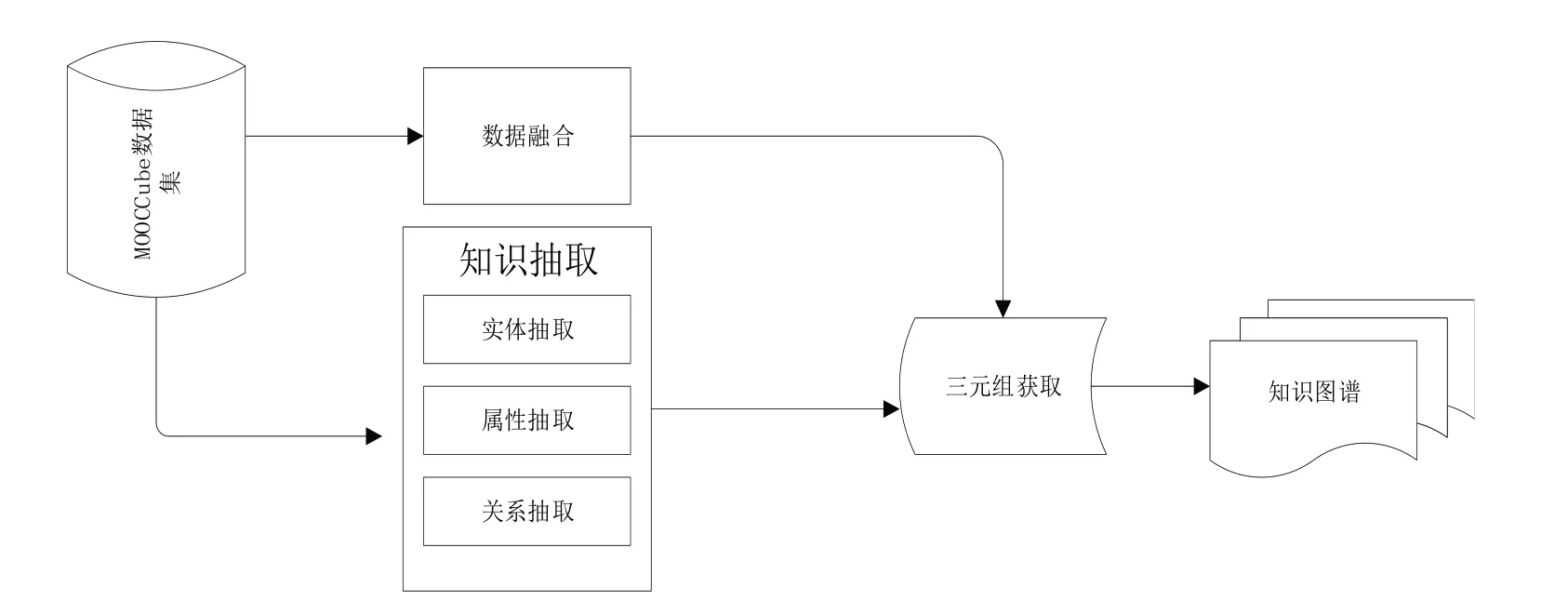
图2 知识图谱构建步骤
首先根据数据的类型不同,用不同的方法对数据进行处理,实现知识的抽取。考虑到不同的课程实体,知识的侧重点不同,将多个课程的知识库进行整合,可以实现课程实体对齐,最终得到一系列三元组。
(1)知识获取。知识抽取主要包括实体抽取、关系抽取。
1)实体抽取。本文实体抽取是从MOOCCube数据集中提取所有课程的学生行为信息,对课程、名称、专业、老师、大学进行抽取,得到实体。
2)关系抽取。对于抽取出的实体,需要找出实体之间的关系。MOOCCube数据集进行预处理后,采用基于规则的关系抽取来遍历文本,将实体之间的关系抽取。例:“民法与生活属于法学”,实体为民法与生活、法学,关系为属于。最终将关系分为授课老师、开设大学、所属专业、包含知识点。
(2)数据整合。将获取的知识进行融合。如表1所示。

表1 课程实体部分片段
(3)三元组获取。对于知识图谱G,由实体—关系—实体三元组(h,r,t)组成,其中h∈ε,r∈β和t∈ε,ε和β分别是知识图谱的课程实体集合和关系集合,利用Neo4j将获取的实体和关系建立三元组,构建知识图谱。例如:“电子科技大学”开设“嵌入式系统设计”,则构成三元组的头实体为电子科技大学,尾实体为嵌入式系统设计,关系为开设。如表2所示。

表2 三元组的构建
完成课程知识图谱的构建后,结合图卷积网络,学习课程知识图谱中语义及用户的潜在兴趣。
2.3 算法流程
本文算法具体流程步骤如下:
(1)建立用户—项目评分矩阵Y,知识图谱G;
(2)遍历交互矩阵Y,计算课程v的感受野S(v);
(3)通过式(1)(2)(3)计算出课程v的邻域表示;
(4)利用式(4)将与课程v进行聚合;
(5)得到最终H阶的课程表示,将其与用户的表示输入预测函数;
(6)重复步骤(2)(3)(4)(5)。
为了提高计算效率,使用负采样策略,完整的损失函数如式(5)所示:
式(5)中ℶ为交叉熵损失,P是负采样分布,Tu是用户u的负采样数。λ是平衡参数,是L2 正则化器。
3 实验与分析
实验采用数据集中包括45 459名用户,25 849个实体,683门课程,4种关系。本文将提出的KGCNMC算法与以下模型进行对比。
(1)MKR[15]利用交叉压缩单元、推荐模型、知识图谱嵌入进行结合来提升推荐效果。
(2)NeuMF[16]利用非线性和线性结合,来学习用户对项目的评分。
(3)UserCF是传统的基于用户的协同过滤算法。
3.1 评价指标
3.2 实验结果
实验数据集按比例6:2:2 划分,分为训练集、测试集、验证集。用户与课程之间存在交互,则为正样本,否则为负样本。KGCN-MC 算法中参数设置维度d=8,感受野深度H=2,其他超参数设置λ1=10-6,λ2=10-2;实验训练迭代100次,取最好的结果作为最终结果。
(1)取不同邻居大小时,对KGCN-MC 算法的推荐效果有影响。实验分析在不同邻居数量n时,KGCN-MC算法的精确率、召回率,邻居数量取值为n∈{1,2,3,4,5}的结果如图3和图4所示。
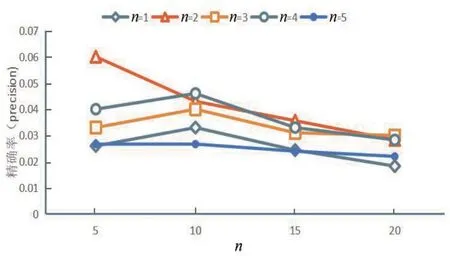
图3 不同数目n的精确率
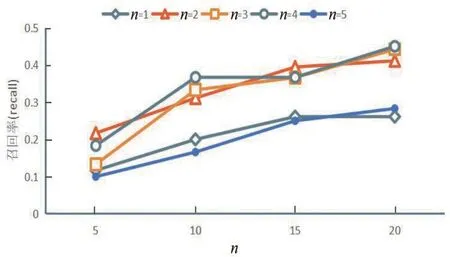
图4 不同数目n的召回率
结果表明,当n取值在2或4时,推荐结果的准确率和召回率最好,因此本文取n=2来进行实验。
(2)将推荐不同数目k时,KGCN-MC算法、MKR、NeuMF、UserCF的精确率、召回率、f1的结果进行对比,精确率、召回率、f1的结果如图5、图6、图7所示。
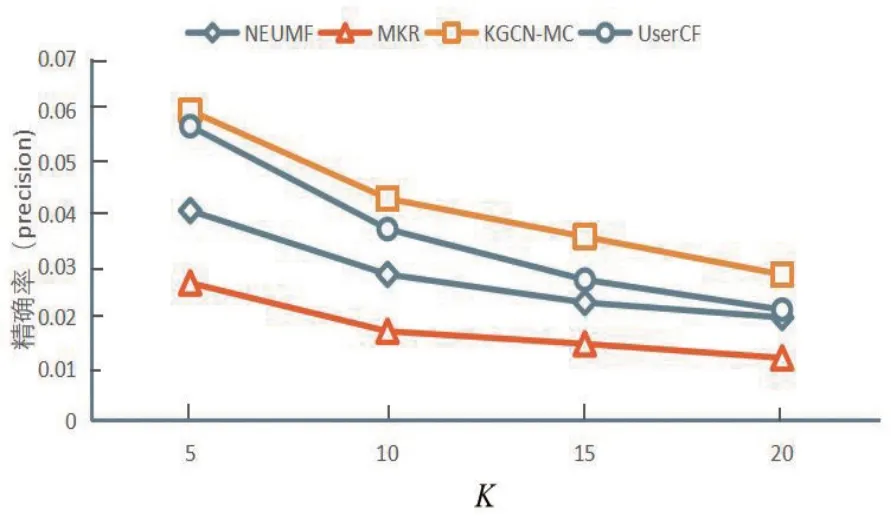
图5 推荐不同数量k的精确率
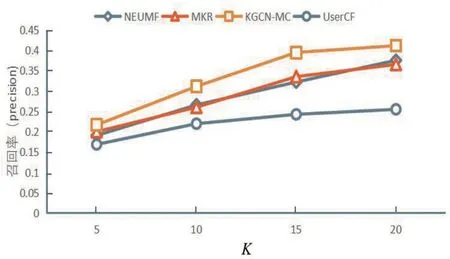
图6 推荐不同数量k的召回率
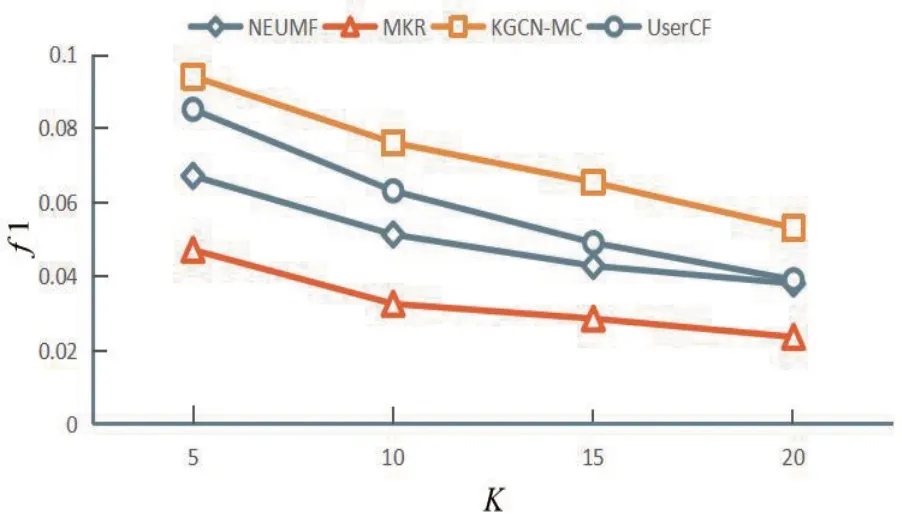
图7 推荐不同数量k的f1
从图5可以看出KGCN-MC算法表现最优,MKR表现最差。图6 recall随着k的增大呈现上升趋势,KGCN-MC算法表现最好,MKR模型其次,UserCF表现最差。图7f1随着k值增大呈下降趋势,在k=10之后下降趋势缓慢,KGCN-MC表现最佳。
实验结果表明,相对UserCF、MKR、NeuMF来说,在用户交互较稀疏的情况下,KGCN-MC算法的推荐效果最好;NeuMF 是一种基于神经网络的推荐,由于用户项目交互记录较为稀疏,且没有知识图谱作为辅助信息,在性能上次于KGCN-MC、UserCF,但加入多层感知机和矩阵分解的情况下,对召回率有所提升。MKR模型将知识图谱作为辅助信息,但没有利用课程之间的语义关系,表现效果最差。所以,加入知识图谱和图卷积网络的KGCN-MC算法,通过课程知识图谱有效地捕获项目之间的相关性,充分利用课程之间的关系;再利用图卷积网络聚合聚合邻域信息,获得用户个性化潜在兴趣在一定程度上能缓解数据稀疏的问题,同时提升推荐效果。
4 结语
考虑现有的推荐算法没有充分利用课程之间的语义关系,无法挖掘课程之间的深层隐含关系问题。本文提出基于知识图谱的MOOC课程推荐算法,将知识图谱作为辅助信息与图卷积网络结合。利用课程实体之间的关系,对特定用户取不同关系的权重,更好地发掘用户的个性化兴趣。实验在数据集上precision、recall、f1上表现出良好的效果,表明KGCN-MC算法比传统的协同过滤算法更佳。但实验仅利用用户的学习时长作为用户的兴趣,并且构建课程实体知识图谱的关系相对较少。下一步的工作是能结合用户个人爱好等作为用户的兴趣,同时构建更加丰富的知识图谱为用户做推荐。
