关于余挠三元组的periodic-模

2019-09-06何东林李煜彦彭康青

五邑大学学报（自然科学版） 2019年3期

何东林，李煜彦，彭康青

（陇南师范高等专科学校数信学院，甘肃陇南 742500）

1 引言与预备知识

Periodic-模在Artin代数表示论和Gorenstein同调代数中扮演着重要角色，其概念最早是由Happel等在文献[1]中引入的.随后，许多作者先后对其进行了研究[2-6]，得到了很好的结论.Bazzoni等[7]研究了关于遗传余挠对的Periodic-模；2014年任伟等[8]讨论了余挠三元组及其应用；2017年狄振兴等[9]提出并研究了Abel范畴上关于余挠三元组的倾斜子范畴.受此启发，本文主要研究关于余挠三元组的Periodic-模.

本文中的环R均指有单位元的结合环，模指酉左R-模.R-Mod表示左R-模范畴，P和I分别表示投射左R-模类和内射左R-模类.设C为R-模类，C的右正交类定义为对任意C∈C都有对偶地，C的左正交类定义为对任意C∈C都有特别地，记设X、Y、Z为3个R-模类.称对子(X，Y)是一个余挠对，如果称余挠对(X，Y)是完全的，如果对任意右R模M都存在正合列0CL→→→M→0和0→M→C′→L′→0，其中C，C′∈Y且L，L′∈X.称余挠对(X，Y)是遗传的，如果对任意如果(X，Y)和(Y，Z)均为余挠对，则称三元组(X，Y，Z)为余挠三元组[8].进而，如果(X，Y)和(Y，Z)均为遗传（完全）余挠对，则称(X，Y，Z)为遗传（完全）余挠三元组.例如：（P，R-Mod，I）为完全遗传余挠三元组，当R是virtually Gorenstein环（该环的概念见文献[10]）时；（GP，GP⊥=⊥GI，GI）为完全遗传余挠三元组，其中GP和GI分别表示Gorenstein投射模组成的类和Gorenstein内射模组成的类.称左R-模短正合列是C-纯的[11]，如果对任意C∈C，都有导出序列仍正合.此时称f为C-纯单同态，g为C-纯满同态且Imf为L的C-纯子模.如果C是有限表示左R-模组成的类，则把C-纯简称纯，C-纯子模简称纯子模.设κ为基数，如果对任意小于κ的极限数λ都有则称集合族是连续的.其余未涉及的概念和记号参见文献[12-13].

2 主要结论

命题1设(X，Y，Z)为遗传余挠三元组，M是Y-periodic 模，则以下结论成立：

1）对任意X∈X和任意非负整数n都有

2）对任意Z∈Z和任意非负整数n都有

证明由M是Y-periodic 模知，存在短正合列(ε):0→M→Y→M→0，其中Y∈Y.

1）对任意X∈X，用函子HomR(X，-)作用于(ε)可得：

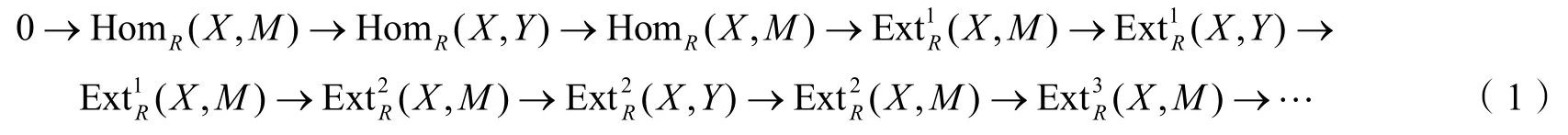
因为(X，Y，Z)为遗传余挠三元组，所以对任意非负整数n都有

2）对任意Z∈Z，用函子HomR(-，Z)作用于(ε)可得：

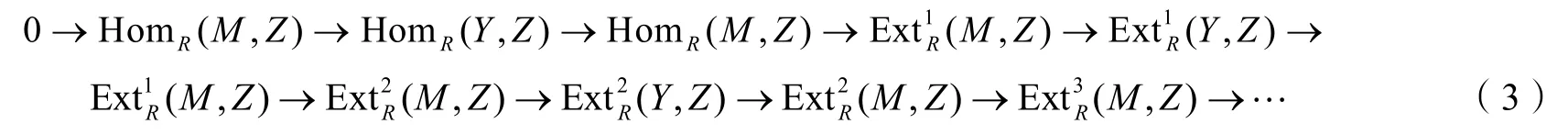
因为(X，Y，Z)为遗传余挠三元组，所以对任意非负整数n都有

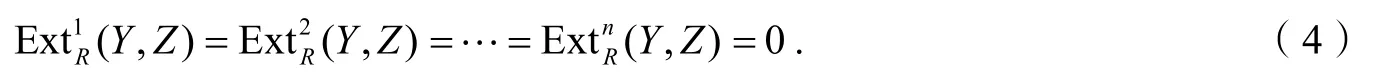
命题2设(X，Y，Z)为遗传余挠三元组，M是Y-periodic 模，0→A→B→C→0是左R-模正合列，则以下结论成立：

1）如果A，B，C∈X，那么若A，B，C中有两项属于⊥M，则第三项也属于⊥M；

2）如果A，B，C∈Z ，那么若A，B，C中有两项属于M⊥，则第三项也属于M⊥.

证明因为(X，Y，Z)为遗传余挠三元组，所以(X，Y)与(Y，Z)均为遗传余挠对.

1）如果A，B，C∈X ，由(X，Y)是遗传余挠对、M是Y-periodic模及文献[7]中引理3.4可知，若A，B，C中有两项属于⊥M，则第三项也属于⊥M.

2）如果A，B，C∈Z，由(Y，Z)是遗传余挠对、M是Y-periodic模及文献[7]中引理3.5可知，若A，B，C中有两项属于M⊥，则第三项也属于M⊥.

定理1设(X，Y，Z)为遗传余挠三元组，Y关于纯满同态像封闭且N是纯子模的并，则

1）如果M是X-periodic 模且对任意α＜λ都有

2）如果M是Z-periodic 模且对任意α＜λ都有

证明1）由(X，Y，Z)为遗传余挠三元组知，Y关于直和封闭.又由假设知Y关于纯满同态像封闭.根据文献[11]中命题33.9易得，Y关于正向极限封闭.当α为后继数时，令当α为极限数时，令易知考虑连续链N也是纯子模的并.由文献[11]中命题33.8知纯子模的并仍为纯子模.可见对任意α＜λ有Vα是N的纯子模，不妨记下面用归纳法证明对任意α≤λ都有

当α为后继数时，结论成立.

当α为极限数时，假设结论对小于α的数均成立.对任意β＜α，考虑如下短正合列：