特征标三元组的本原诱导子

黄谦，王丽凤

（山西大学 数学科学学院，山西 太原 030006）

0 引言

本文仅讨论有限群和复特征标，所采用的群论和特征标的术语和符号分别取自Isaacs的经典教材[1-2]。特别地，对任意群G，我们用Irr(G)表示G的所有不可约特征标的集合。称T=(G，N，θ)为一个特征标三元组，如果G为任意群，N⊲G为G的正规子群，θ∈Irr(N)为N的一个不可约特征标且为G-不变的。

特征标三元组是群表示论中重要的研究对象，具有丰富的内容和深刻的成果，以及重要而广泛的应用。例如，近年来关于群表示论中著名的McKay猜想取得了一系列重大进展，在约化为单群的过程中，特征标三元组的诱导子技术和上同调理论即发挥了核心作用，相关的具体内容和前沿文献可参考Navarro的最新专著[3]。关于特征标三元组的最新研究成果可以参考相关文献[4-6]。

本文将采用范畴的观点，把特征标三元组视为基本的研究对象，主要研究特征标三元组的本原诱导子，特别是本原诱导子的次数问题。事实上，Dade在系列论文中[7-9]针对特征三元组的诱导子创立了稳定子极限理论，并用之研究M-群的若干著名猜想。Isaacs简化了Dade的诱导子定理[10]，并给出了关于不可约特征标的本原诱导次数问题的一个应用。此外，Loukaki也研究了一种新型的诱导子极限，即所谓的线性极限[11]，并与Dade等[12]对线性极限做了系统地探讨。总之，研究本原诱导子的次数问题，不仅是一种新型的证明技术，而且可用来解决群表示理论中的相关重要问题。这些课题可以参考相关文献[13-14]。

为叙述本文主要结果，我们先给出Dade和Isaacs在上述文献中引入的若干基本概念。

固定一个特征标三元组T=(G，N，θ)。如果R=(H，M，φ)也是一个特征标三元组，使得G=NH，M=N∩H，并且φ在θ下方，即φ是限制特征标θM的一个不可约分量，则称R为T的一个子三元组，记为R≤T，如图1所示。

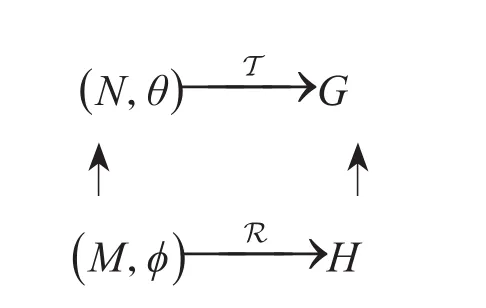
图1 子三元组Fig.1 Character subtriple

进而，如果还有φN=θ，则称R为T的一个诱导子；如果φ=θM，则称R为T的一个限制子。特别地，如果T没有真诱导子，即T不存在诱导子T′=(G'，N'，θ')使得G'＜G，则称 T是本原的。方便起见，我们称θ(1)为特征标三元组 T=(G，N，θ)的次数，记之为degT=θ(1)。

有了以上准备，本文所研究的具体问题，可概述如下：

研究问题设T=(G，N，θ)为一个特征标三元组，探讨在什么条件下T的任意两个本原诱导子S1=(H1，M1，φ1)和S2=(H2，M2，φ2)均 有 相 同 的 次数，即φ1(1)=φ2(1)。

Isaacs在[10]中的主要结果即定理3.1，证明了当N是幂零群时，则上述问题有肯定的解答，即T=(G，N，θ)的任意两个本原诱导子均有相同的次数。

本文主要结果是减弱了上述Isaacs定理中N为幂零群的条件，通过定义特征标三元组的正规子三元组和次正规子三元组的概念，给出了上述研究问题的一个解答，从而推广了Isaacs的主要结果。本文主要结果如下：

定理A设T=(G，N，θ)为特征标三元组，其中N为可解群。如果满足下述两个条件：

（1）T的每个本原的子三元组都是次正规的；

（2）T的每个本原的子三元组的所有极大正规限制子也都是本原的，则T的任意两个本原诱导子均有相同的次数。

在上述定理A中，当N是幂零群时，则条件（1）自动满足。事实上，我们将证明一个本原的三元组，如果是幂零的，则条件（2）也自动成立。作为定理A的一个应用，我们可简化条件（2），在使用时可能更为便利些。我们称一个特征标三元组T=(G，N，θ)是幂零的，如果N/Z(θ)为幂零群。

定理B设T=(G，N，θ)为特征标三元组，其中N为可解群。如果T的每个本原的子三元组都是幂零的和次正规的，则T的任意两个本原诱导子均有相同的次数。

在特征标的诱导理论中，我们还研究一个给定的不可约特征标χ∈Irr(G)，何时具有相同的诱导次数，即如果χ=(ξ1)G=(ξ2)G均可以从子群Hi≤G的本原特征标ξi∈Irr(Hi)诱导，其中i=1，2，研究在什么条件下总有ξ1(1)=ξ2(2)。作为特征标三元组诱导子的一个应用，Isaacs在[10]中的定理B，给出了一个充分条件，即χ在G的Fitting子群上限制不可约时，则诱导χ的所有本原特征标均有相同的次数。

作为定理B的一个应用，下述结果同样推广了Isaacs的定理B。

定理C设G为任意群，χ∈Irr(G)。如果G存在一个可解正规子群N，使得θ=χN不可约，并且特征标三元组T=(G，N，θ)的每个本原的子三元组都是幂零的和次正规的，则诱导χ的所有本原特征标均有相同的次数。

本文所需的预备知识和基本结果我们将在第1节给出，在第2节将证明上述三个主要定理。

1 预备知识

为了推广Isaacs在[10]中的主要定理，我们引入下述概念。

定义1设S=(H，M，φ)为特征标三元组T=(G，N，θ)的一个子三元组。

（1）如果M⊲N，则称S为T的一个正规子三元组，记为S⊲T。

（2）如果存在一个子三元组序列：

则称S为T的一个次正规的子三元组，记为S⊲⊲T。

（3）如果N=Z(θ)M，则称S为 T的一个覆盖子。

Isaacs在[10]中还定义了特征标三元组的拟本原性。设T=(G，N，θ)为一个特征标三元组，如果对任意M≤N且M⊲G，均有θM为齐次的特征标，即θM=eφ，其中e为正整数而φ∈Irr(M)，则称 T是拟本原的。不难证明拟本原的特征标三元组必然也是本原的，但反之一般不成立。

关于拟本原的特征标三元组，我们有下面一个基本性质。

引理1设T=(G，N，θ)为拟本原的特征标三元组，如果N/Z(θ)是幂零群，则N/Z(θ)为交换群。

证明因为θ是G-不变的，故Kerθ为G的正规子群，从而所给条件和所证结论可以在商群G/Kerθ中考虑，不失一般性，可设 Kerθ=1，就有Z(θ)=Z(N)。进而N/Z(θ)=N/Z(N)。因为N/Z(θ)是幂零的，故可得N幂零。任取A是N的特征子群且A是交换群，则A⊲G。又因为T=(G，N，θ)为拟本原，就有θA=eα齐次，其中e为正整数，α∈Irr(A)。但Kerα=A∩Kerθ=1，即α为A的一个忠实线性特征标。显然θ的G-不变性得出α亦如此，所以αg(a)=α(a)，对任意g∈G和a∈A均成立，据此可知α(gag-1a-1)=1，再从α的忠实性推出gag-1a-1=1，亦即ga=ag，于是有A≤Z(θ)=Z(N)，即Z(N)是N的唯一极大交换特征子群，从而N的幂零类小于等于2。等价于说N/Z(θ)为交换群。

在定理A的证明中，我们要用到下述关于诱导子和限制子的一个对应关系。

引理2设T=(G，N，θ)为特征标三元组，并且R=(H，M，φ)为 T的 一 个 限制子。如 果 T′=(G'，N'，θ')为 T的一个诱导子，则唯一对应 R的一个诱导子

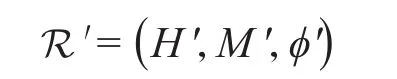
使得R′也是T′的一个限制子，其中H'=H∩G'，M'=M∩N'且φ'=θ'M'。

证 明由 R=(H，M，φ)为T的限制子知θM=φ，由T′=(G'，N'，θ')为 T的诱导子知(θ')N=θ，即θ'M不可约，由Mackey公式得出N'M=N且(θ'M')M=φ，由此可推出(φ')M=φ不可约，如图2所示。

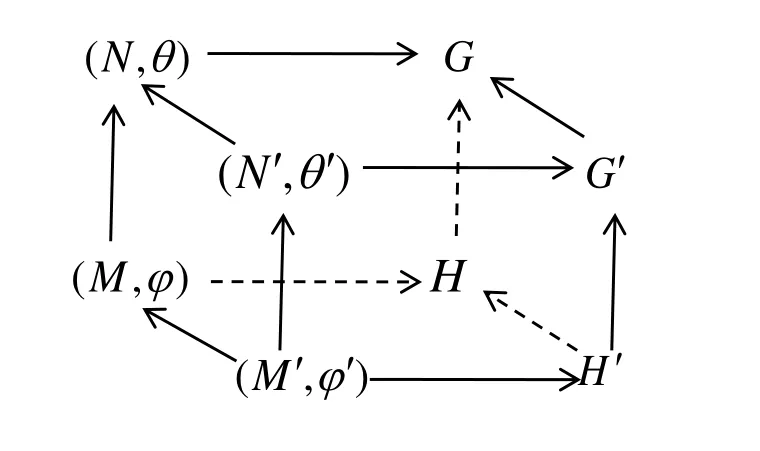
图2 对应关系Fig.2 Correspondence relationship

验证M∩H'=M'且MH'=H。按定义，我们有：

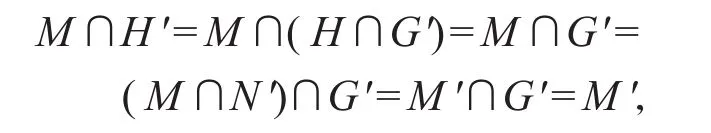
因G=G'N=G'N'M=G'M，由模律有

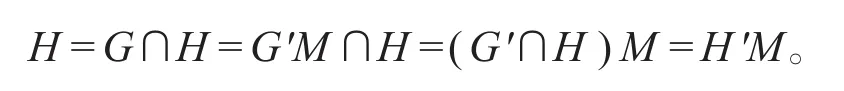
下面验证 R′=(H'，M'，φ')为特征标三元组。根据上述子群关系，从M⊲H知M'⊲H'，再从θ'是G'-不变的以及φ'=θ'M'，可知φ'也是H'-不变的，表明 R′=(H'，M'，φ')为一个特征标三元组，按定义即为R的一个诱导子。

最后验证 R′=(H'，M'，φ')为 T′=(G'，N'，θ')的一个限制子。先证明N'∩H'=M'且N'H'=G'，按定义N'∩H'=N'∩(H∩G')=N'∩H=(N′∩N)∩H=N'∩M=M'此外，从G=NH=N'MH=N'H可 知N'H'=N'(H∩G')=(N'H)∩G'=G∩G'=G'由条件可知φ'=θ'M'，即证得R′=(H'，M'，φ') 为 T′=(G'，N'，θ')的一个限制子。

在定理B的证明中，我们需要[15]中定理2.4关于覆盖子的一个结果。

引理3设S≤T=(G，N，θ)为一个覆盖子，如果T是本原的，则S也是本原的。

2 主要结果

我们先证明本文定理A，为方便起见，重述如下：

定理1设T=(G，N，θ)为特征标三元组，其中N为可解群。如果满足下述两个条件：

（1）T的每个本原的子三元组都是次正规的；

（2）T的每个本原的子三元组的所有极大正规限制子也都是本原的，则T的任意两个本原诱导子均有相同的次数。

证明设Si=(Hi，Mi，φi)为T的任意两个本原诱导子，其中i=1，2。我们将对|N|作归纳，证明degS1=degS2，即证φ1(1)=φ2(1)。

如果M1=N，则T=S1也是本原的，从而T没有真诱 导 子 ，迫 使 T=S2，此 时φ1=θ=φ2，故 degS1=degS2，结论成立。同理可证如果M2=N，结论也成立。

以下设每个Mi＜N，即Si＜T。按假设T的每个本原诱导子均为次正规子组，所以每个本原三元组Si均包含在T的某个极大正规子三元组Ri中：

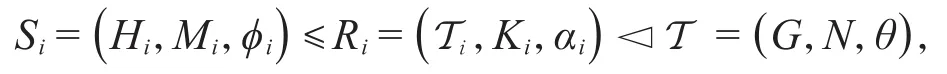
其中Ki⊲N且Ki＜N，Ti=KiHi，并且αi=(φi)Ki。因为Ki⊲ Ti且NTi=G，故Ki⊲G。此时从 Ri为 T 的极大正规子三元组可知N/Ki均为G的主因子。此外，从定义可知每个Si都是Ri的本原诱导子，而每个Ri也都是T的诱导子，如图3所示。

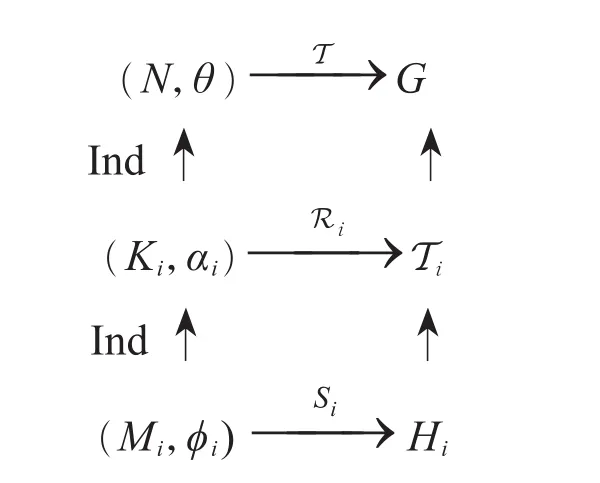
图3 本原诱导子Fig.3 Primitive inductors

以下我们分两种情形讨论。

（1）假设K1=K2。

此时α1和α2都是θK1的不可约分量，因为K1是N的正规子群，根据Clifford定理，可知α1和α2在N中共轭，故存在某个n∈N使得(α2)n=α1。简单计，我 们 用R2的N-共 轭(R2)n=(T2n，K2n，α2n)替 代R2，相应地用S2的N-共轭 (S2)n=(H2n，M2n，φ2n)替代S2，由于 deg(S2)n=α2n(1)=α2(1)=degS2并不会影响所证结论，故可以假设α2=α1。在此情形下，注意到(T1，K1，α1)和(T2，K1，α1)都是 T 的诱导子，考虑α1在G中惯性群IG(α1)。一方面，从(α1)N=θ不可约，可知N∩IG(α1)=IN(α1)=K1。另一方面，从α1都是 Ti-不变的，可知每个 Ti≤IG(α1)。使用模律，我们有

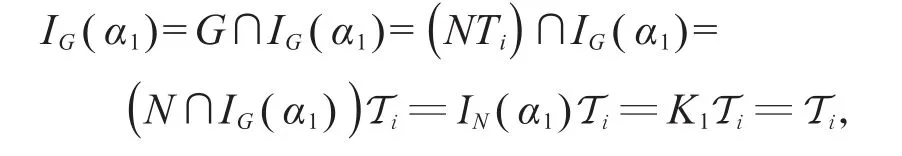
所以T1=T2，亦即R1=R2。此时S1和S2均为R1的本原诱导子，但K1＜N，不难看出Ri的本原子三元组也都是T的本原子三元组，故定理的两个条件对Ri均遗传，根据归纳假设，我们有degS1=degS2，表明所证结论成立。

（2）假设K1≠K2。

记D=K1∩K2。因为N/Ki都是G的主因子，并且K1＜K1K2≤N均为G的正规子群，只有K1K2=N。注意到(α1)N=θ=(α2)N，我们有

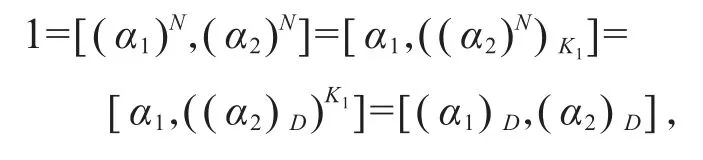
据此得出(α1)D和(α2)D有唯一共同的不可约分量γ，且重数均为1。

令S=T1∩T2。因S固定α1和α2，也固定正规子群D，并且(α1)D和(α2)D有唯一的相同不可约分量γ，故S也固定γ，表明(S，D，γ)也是一个特征标三元组，我们令

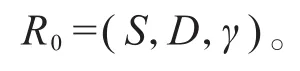
验证R0≤R1。因为γ在α1的下方，我们只需验证子群关系K1S=T1且K1∩S=D。事实上，从G=NT2=K1K2T2=K1T2，使用模律推出

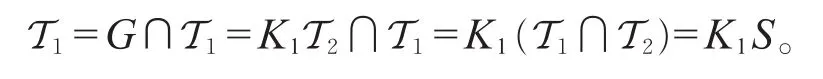
进而，可直接验证

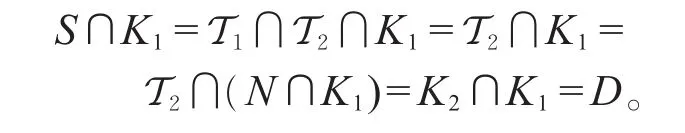
再验证R0≤R2。因为γ也在α2的下方，只需验证子群关系K2S=T2且K2∩S=D。

同样地，由于G=NT1=K1K2T1=K2T1，使用模律又可得到

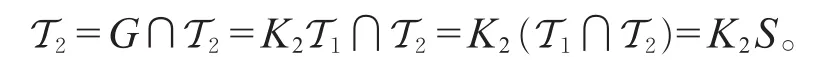
进而，我们也有所需的子群关系：

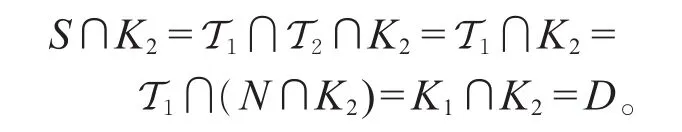
相关子群和特征标的位置关系如图4所示。

为完成所证，我们再区分两种情形讨论。

（a）假设γN不可约。此时γKi均不可约，其中i=1，2，因为αi均在γ上方，只有γKi=αi。上述已证 R0是每个Ri的子三元组，故R0均为Ri的诱导子。任取S0是R0的一个本原诱导子，则S0和S1均为R1的本原诱导子，但|K1|＜|N|，根据归纳假设，则degS0=degS1。同理，由于S0和S2均为R2的本原诱导子，但|K2|＜|N|，仍从归纳假设得到degS0=degS2。至此即证degS1=degS2，故结论成立。

（b）假设γN可约。我们先验证R0分别是R1和R2的一个极大正规限制子。注意到(αi)N=θ，故γKi必然是可约的，否则γKi=αi，导致γN=θ，与假设矛盾。因为N/K1是G的主因子，而N是可解群，故N/K1为交换群，从而是一个单G-模。又因为G=T2N，而N在N/K1上作用平凡，故N/K1也是一个单T2-模。但N/K1和K2/D同构，该同构显然和T2交换，故K2/D也是T2的一个主因子。显然D⊲K2，表明R0是R2的一个极大正规子三元组。由于[(α2)D，γ]=1且γK2≠α2，由特征标的下降定理，只有(α2)D=γ，表明R0是R2的一个限制子。至此即证R0是R2的一个极大正规限制子，同理可证故K1/D也是T1的一个主因子，从而R0也是R1的一个极大正规限制子。

根据引理2，因为 R0=(S，D，γ) 是 R1=(T1，K1，α1)的限制子，而S1=(H1，M1，φ1)是R1的诱导子，故可唯一对应R0的一个诱导子S1*=(H1*，M1*，φ1*)，并且S1*也是S1的一个限制子。此时degS1=degS1*，如图5所示。

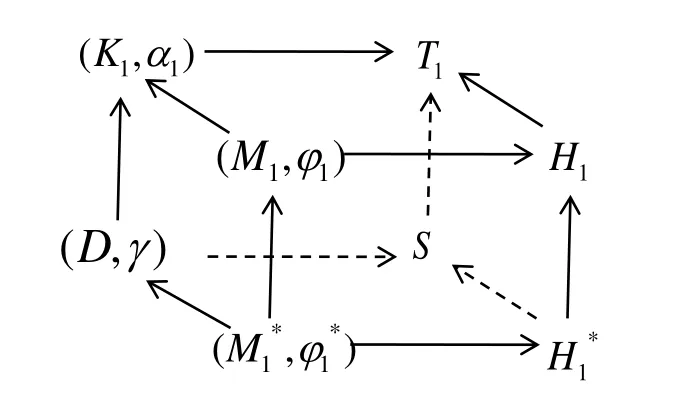
图5 限制子和诱导子Fig.5 Restrictor and inductor

在此情形下，注意到DM1=K1且D∩M1=M1*，但D⊲K1，所以M1*⊲M1。又因为 T1=K1H1，上述已证K1/D为T1的主因子，而K1≤N也是可解群，故K1/D只能是初等交换群，表明K1在K1/D上的共轭作用平凡，所以K1/D是单H1-模。进而，不难看出K1/D和M1/M1*是H1-同构的，故M1/M1*也是H1-单模，等价于说S1*是S1的一个极大正规子三元组，从而是一个极大正规限制子。根据条件（2），从S1为T的本原诱导子可知S1*也是本原的，显然是R0的一个本原诱导子。

再从S1和S2的对称地位，同理可证S2存在一个极大正规限制子S2*，同时也是R0的一个本原诱导子。特别地，我们有degS2=degS2*。

因为R0≤T，故R0的每个本原子三元组也都是T的本原子三元组，但|D|＜|N|，故从归纳假设可知R0的两个本原诱导子S1*和S2*具有相同的次数，即degS1*=degS2*，从而degS1=degS2至此完成证明。

作为上述定理1的一个应用，我们证明本文定理B。

定理2设T=(G，N，θ)为特征标三元组，其中N为可解群。如果T的每个本原的子三元组都是幂零的和次正规的，则T的任意两个本原诱导子均有相同的次数。

证明根据定理1，我们只需证明T的任意一个本原的子三元组S=(H，M，φ)的每个极大正规限制子S*=(H*，M*，φ*)也都是本原的。

按假设S是幂零的，即M/Z(φ)是幂零群，因为S是本原的，故也是拟本原的，根据引理1，则M/Z(φ)为交换群，再从[1]中定理2.31推出φ在Z(φ)上完全分歧。特别地，我们有φ(M-Z(φ))=0。

因为S*是S的极大正规子三元组，即M*⊲M且M/M*为H的主因子。但Z(φ)⊲H，故M*≤Z(φ)M*≤M。在此出现两种情形：或者Z(φ)M*=M，或者M*=Z(φ)M*亦即Z(φ)≤M*。

如果Z(φ)M*=M，则S*覆盖S，根据引理3，此时从S的本原性可推出S*也是本原的，结论成立。

如果Z(φ)≤M*，上述已证φ(M-Z(φ))=0，则。根据[1]中引理2.29，由于φ是φ*的扩张，我们有1=[φ*，φ*]=|M：M*|[φ，φ]=|M：M*|，故M*=M，表 明S*=S也是本原的，结论亦成立。

使用定理2可证明本文定理C。

定理3设G为任意群，χ∈Irr(G)。如果G存在一个可解正规子群N，使得θ=χN不可约，并且特征标三元组T=(G，N，θ)的每个本原的子三元组都是幂零的和次正规的，则诱导χ的所有本原特征标均有相同的次数。

证 明设χ=(ξ1)G=(ξ2)G，其中Hi≤G且ξi∈Irr(Hi)均为本原特征标，i=1，2。我们将证明ξ1(1)=ξ2(1)。

令Mi=N∩Hi，则Mi⊲Hi。因为ξi也是拟本原的特征标，可设φi是ξi在Mi限制的唯一不可约分量，则φi必然是Hi-不变的，从而Si=(Hi，Mi，φi)均为特征标三元组。注意到((ξi)G)N=χN=θ不可约，根据特征标的Mackey公式，则NHi=G，并且

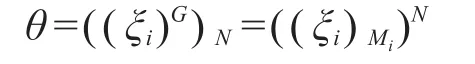
也不可约，迫使(ξi)Mi=φi且(φi)N=θ，表明Si均为T的诱导子。但ξi∈Irr(Hi|φi)均为本原特征标，不能从真子群诱导，根据特征标的诱导对应（见[16]中引理2.11（b）），可知Si也是本原诱导子。最后，再使 用 定 理 2 得 到 degS1=degS2，即ξ1(1)=φ1(1)=φ2(1)=ξ2(1)，结论成立。