巧用学习材料 赋能数学建模
——《倍的认识》教学设计与评析
2023-09-01执教严庆评析倪芳华
执教 严庆 评析 倪芳华
【教学内容】
苏教版三年级上册第4~6 页例3 和“想想做做”第1~4 题。
【教学过程】
一、复习铺垫,回忆算法
口答下面填空题
3 个5 是()
8 里面有()个2
【评析:口答填空题,从学生已有认知出发,旨在衔接旧知,对接经验,引发学生对“求几个几相加用乘法计算”和“求一个数里面有几个另一个数,用除法计算”的回忆和思考,为新知的学习做好铺垫。】
二、自主探究,构建新知
1.出示主题图
(1)自主探究

学生汇报:一号花坛里有2朵蓝花,6 朵红花。红花比蓝花多4 朵,还可以说蓝花比红花少4朵。算式:6-2=4(朵)。
(2)引入新课
师:我们已经学过用多或少来表示数量之间的关系,其实数量之间还可以用“倍”来表示,想知道怎么表示吗?我们一起来研究。(板书课题:倍的认识)
2.初步建立“倍”的概念
(1)初步感知
师:如果把2 朵蓝花圈起来表示1 份,红花有这样的几份呢?

①在《作业纸》上圈一圈、数一数、画一画。
②交流:是怎样圈的?几朵一圈?红花圈了这样的几份?
指出:把2 朵蓝花看作1 份,红花有这样的3 份;也就是说红花有3 个2 朵,可以说成红花的朵数是蓝花的3 倍。
(2)自主构建
出示:蓝花2 朵,红花8 朵。
提问:蓝花2 朵。红花比原来的多了2 朵,现在红花是蓝花的几倍呢?
请大家在《作业纸》上圈一圈、填一填。红花有( )个2 朵,红花的朵数是蓝花的( )倍。
(3)探索算法
师:如果分别用○和△表示蓝花和红花的朵数,你能在《作业纸》上表示红花是蓝花的6 倍吗?

师:蓝花有2 朵,红花有12朵,12 里面有几个2?除了圈一圈,还可以用什么方法计算?
师:12÷2=6。这里的12 表示什么?2 和6 呢?注意“倍”表示两个数量之间的关系,不是具体的数量,所以得数后面不需要写“倍”。
比较:这3 道题都是把什么看作一份数?什么没有变?什么变了?为什么?
小结:刚才我们都是把蓝花看作一份,红花有这样的几份就是蓝花的几倍。
【评析:课始,教师创设了两个量比较的问题情境,从“差比”过渡到“倍比”,构建了新旧知识的关联。通过圈一圈把蓝花圈成1份,红花有这样的3 份;红花有3个2 朵,引出“倍”:红花的朵数是蓝花的3 倍。接着,标准量也就是一份量不变,比较量变成8 朵、12朵,在圈一圈、画一画、摆一摆、比一比等数学活动中,让学生感受到随着红花朵数的改变,红花与蓝花的倍数关系也在变。理解“几倍”与“几个几”之间的联系。初步建立“倍”的认知模型。借助直观图,再算一算,将学生的关注点引导到“一个量里包含几个另一个量就是它的几倍”,帮助学生建立“倍”的概念意义。】
3.深刻理解“倍”的概念
师:接着我们来研究二号花坛里的数学问题。有3 朵蓝花,6 朵红花。红花的朵数还是蓝花的3 倍吗?先圈一圈,再和同桌说一说。
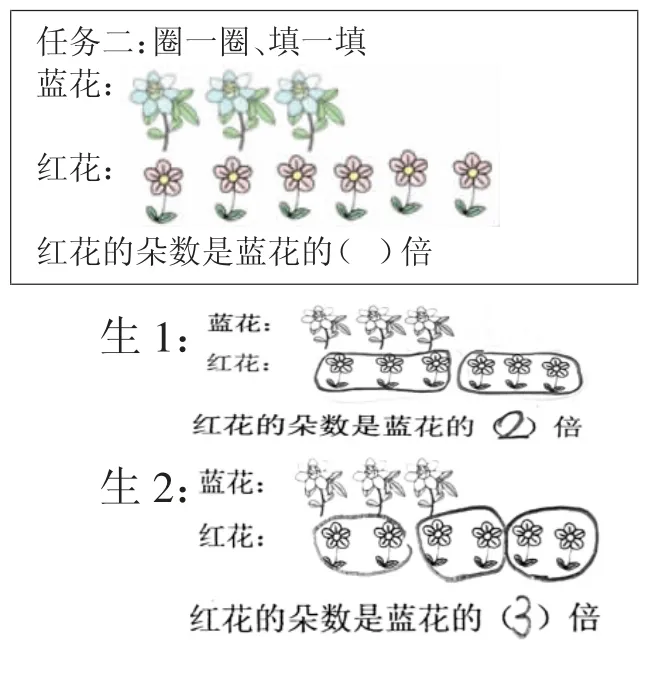
提问:为什么是2 倍而不是3倍呢?
学生汇报:这里蓝花的一份是3 朵,红花3 朵一圈,圈了2份,红花有2 个3 朵,就说红花是蓝花的2 倍。
强调:这里是把3 朵蓝花看作一份,红花有这样的几个3,就是几倍。倍数是以谁为一份,它有这样的几份。在圈的时候不能随意去圈,要根据一份的朵数来圈。
师:红花不变,如果蓝花变成1 朵,红花是蓝花的几倍?如果蓝花变成6 朵,红花是蓝花的几倍?你能用圆片和三角摆一摆或画一画其他倍数吗?
课件出示:


指出:比较量没变,一份的量变了,它们之间的倍数关系也就变了。看来,我们在比较的时候,确定一份的量很重要。第4 幅作品,“1 倍”说明两种花的朵数同样多。可以说成红花是蓝花的1 倍,也可以说成蓝花是红花的1 倍。
归纳小结:把一个数量看作一份,另一个数量有这样的几份,就是它的几倍,可以用除法计算。
4.在变化中发展“倍”
师:任务二中要想变成红花的朵数是蓝花的3 倍,蓝花不变,红花应该怎么办?蓝花变成1 朵呢?红花怎么办?
生1:蓝花不变,再增加3 朵红花,红花的朵数就是蓝花的3 倍。
生2:蓝花变成1 朵时,去掉3 朵红花,红花的朵数就是蓝花的3 倍。
师:现在蓝花不变,红花增加1 朵,还能用整数倍表示吗?
师:当我们无法用整数倍表示的时候,可以用几倍多几或几倍少几来表示。
小结:倍数和比多少虽然都是比较关系,但是是有区别的。比多少表示多几个或少几个,而倍数是以谁为一份,它有这样的几份。
【评析:在研究二号花坛里两种花的倍数关系时,教师分别呈现了一个正例和一个错例,在新的矛盾冲突中,促使学生在比较中思考,体会“一份数”与“几份数”之间的关系。接着,教师设计了三个层次的研学活动,引发学生进行深度学习,学会深度思考。一是比较量不变,标准量改变;二是标准量、比较量都改变,但都是3 倍关系;三是两个量不是整倍数的关系。学生在做中学、学中思、思中做,进一步明确两个量比较时,把数量少的看作一份,另一个量有这样的几份就是几倍。让学生在“变”与“不变”中,深刻理解“倍”的意义,形成“倍”的思维模型。】
三、巩固练习,拓展延伸
1.填一填

下面带子的长度是上面带子的( )倍。
(2)先量一量,再填一填。求出第一条线段的长度是第二条的多少倍。(课件演示将带子直条图变成线段图)

2.算一算
(1)看下图,这里散落摆放的花朵,你能用什么方法很快知道红花的朵数是蓝花的几倍?(12 里面有几个3,用除法计算)

(2)月季花7 盆,菊花35 盆,菊花的盆数是月季花的几倍?(图略)
3.画一画
请设计一个你喜欢的倍数,并说一说。
【评析:巩固练习的三个层次,运用“倍”的知识进行判断、操作、运算、创造,深化“倍”的认识,培养学生的应用意识和数学素养。在图像表征、操作表征、语言表征等多元表征中,凸显“倍”的本质,“倍”如同比多少一样,都是比较两个量时得到的一种关系,但本质是不一样的。倍数关系是由标准量和比较量共同决定的。抽象的数学概念教学在有趣的情境、丰富的活动、多维的思考中落地生根。】
四、回顾总结,提升认识
师:今天我们学习了什么新知识,你对“倍”有哪些认识?我们通过什么方法来认识“倍”呢?生活中“倍”的现象也很多,请同学们试着找一找、说一说。
【课后总评】
《倍的认识》是学生构建乘法结构的关键课,具有重要的研究意义和价值。本节课的起点是学生已经会比较两个数量之间的相差关系及已有表内乘除法的认识。教学时,教师借助知识迁移从“差比”引入“倍比”,精选鲜活的学习素材,采用动作表征、形象表征、符号表征、言语表征等多元表征,促进概念的意义建构,巧设练习实现概念巩固和深化。整节课,教师引领着学生较好地经历了“倍”概念的形成过程,建构了“倍”的数学模型。
一、任务驱动,开启思维之门
问题是数学的心脏。思维因问题而发动,因问题而深入。“倍”的概念源于比较,课始,教师设计研学任务,激发学生原有的经验,两个数量的比较可用“相差关系”表示,还可用“倍数关系”表示,从而引出“倍”的概念。先利用“几个几”引出“倍”的含义,再从除法的角度解读“倍”的概念。当比较量(6 朵红花)没变,一份的量(2 朵蓝花)变了,倍数会发生怎样的变化呢?引导学生在错例辨析和自主操作中,打破思维定势,让“倍”的表象在头脑中更清晰,体会到以一个数为标准,另一个数里有这样的几份就是它的几倍,并在数学学习中学会思维。
二、情境创设,引领思维进阶
用真实情境与核心问题引发和驱动数学思维。教师抓住了情境脉络和认知脉络两条线有序组织教学活动。在真实有效的情境中渗透着审美教育和劳动教育,以两个花坛里的蓝花和红花的朵数为素材,巧设变式训练,激活学生思维。在变换的现实情境中,让学生深刻感悟到“倍”是比出来的,“倍”跟“几个几”有关系,“倍”可以看作一种运算。教师把准了认知起点,课前,复习旧知,回忆了算法;课始,从“差比”引出“倍比”,在多维表征中,初步建立“倍”的模型;课中,在“变”与“不变”的比较辨析中,在数与形的对应转换中,深刻理解“倍”概念的本质;课后,在填一填、算一算、画一画等多样性、趣味性的练习中,提升学生持续学习的能力。找一找生活中“倍”的现象,让学生用数学的眼光去观察生活,感受数学就在身边。
三、学习进阶,提升数学素养
教师精心设计了相互联系、步步递进的学习任务,促进学生的数学认知、思维不断进阶。一是搭建思维支架,让学习真正发生。先从两种花的数量比较开始,打通新旧知识跨越进阶的节点;再进行灵活的变式学习活动:标准量不变、比较量变化;标准量变化、比较量不变;标准量和比较量都变化。催生学生深度思考、探究,促进学习不断进阶。二是搭建知识支架,让思维更加有效。教师巧妙选用学习材料,联通生活经验,从实物到图形,从图形到线段,从操作到计算,实现从直观思维向抽象思维发展。在实际操作中,让概念可视化。在辨析异同中,发展推理能力。在“学思行”融合中,把握“倍”概念的本质,“求一个数是另一个数的几倍”,实际是“求一个数里有几个另一个数”。逐步感悟比较、抽象、归纳等数学思想,推动学生的认知水平“拾级而上”,实现学生数学思维的有效进阶。
