经历再造过程 体悟算法优化——《乘法的初步认识》教学实践与思考（二）

文|徐 浩

【教学内容】

人教版二年级上册第四单元第一课时。

【课前思考】

在学习《乘法的初步认识》一课之前，学生已经学习了100 以内的加法和减法。乘法与加减法同属于四则运算，在运算的意义上与加法非常相似。但若是追溯乘法与加法的产生，意义是完全不同的。加法和减法的产生，是人类对自然界“分与合”这一类现象的抽象刻画。乘法的本质也是一种“特殊的合”，那么学生自然而然就会有“已经有加法了为什么还需要乘法”这样的疑问。通常，教师给与的回答是“为了简便”，而且通常是在将乘法算式和夸张的连加算式放在一起做比较之后，理所当然地给出“因为简便”这样容易让学生接受的回答。但是笔者认为，这样先揭示乘法再对比突出优越性的方式，似乎在逻辑上是反的。而且往往会让学生忽略一个至关重要的问题——“我在什么样的情况下应该想到用这样创造性的方式解决问题？”

乘法真实的产生应该是在发现了相同加数连加这一类加法算式的规律，得到“计算的结果只跟加数本身和加数的个数有关”这一重要结论之后，继而想到优化此类加法算式的算法，从而得到新的运算方法——乘法。学生应该经历：探究发现规律，探讨得到结论，再想到“创造新的运算”来解决问题的逻辑过程。经历这样的探究过程虽然困难，但是非常有必要。四则运算不是运算的全部，人类社会的发展一定还会遇到需要新的运算方式的时候。我们需要引导学生意识到，当现有的运算方式遇到困难时，可以想一想能不能找到某种规律，创造一种全新的运算或方式来解决问题。如果说，教给学生加法，是为了让学生能够想到用抽象的数学符号来刻画现实世界。那么教给学生乘法，就应该是为了让学生能够想到用新的数学符号来优化数学世界。这样的创新意识，也是《义务教育数学课程标准（2022 年版）》强调的核心素养的主要表现之一。

【教学目标】

1.感受乘法的产生历程，体会乘法产生的必要性。

2.了解乘法的意义，认识乘号，会读、写乘法算式，会把相同加数连加算式改写成乘法算式。

3.培养符号意识和创新意识，勇于探索，提出对后续数学运算的猜想。

【教学过程】

一、游戏引入，引发思考

将学生分为男女两组进行游戏。

游戏规则：男女两组分别观察课件动画中逐个闪现的数字，顺利写出相应的加法算式，率先算对结果的小组获胜。

回合一：

2+1+7+4+5 vs 2+2+2+2+2

回合二：

5+5+3+9+6 vs 5+5+5+5+5

师：相同加数的加法算式很有特点，似乎在计算上都比杂乱无章的加法算式要容易。这节课就让我们一起来研究相同加数加法算式的奥秘！

【思考：采用游戏的方式以及卡通数字，激发学生学习的兴趣。在游戏的“不公平”中体会相同加数加法算式的特别。同时通过第二组数据，有几个加数相同和全部加数相同的加法算式做对比，强化今天学习的内容：相同加数加法的认知。自然地引出对于这类算式的探究，为后续深入学习做好铺垫。】

二、对比分析，探究“和”的秘密

2+2+2+2+2=10

5+5+5+5+5=25

师：探究奥秘往往是从相同点和不同点入手，上面两个算式的相同点与不同点分别是什么？

生：相同点：都是加数相同的加法算式、加数的个数都是5 个；不同点：加数不同、和不同。

师：它们明明都是“5 个”加数，为什么“和”会不同呢？

生：因为加数不同，一个加数是2，一个加数是5。

得到结论：看来加数相同的加法算式的和与加数是多少有关。

师：加数相同的加法算式的和是不是只与加数是多少有关？

生：不是！还与加数的个数有关，例如这里5 个2 相加的和是10，如果改成4 个2 或者6 个2，和就会发生相应的改变。

优化结论：加数相同的加法算式的和，与加数本身是多少有关，也与加数的个数有关。

师：除了加数本身和加数的个数，还有别的因素会影响到加数相同的加法算式的和吗？

生：没有了。

举例论证：3 个3，有没有哪个同学的3 个3 的和与别人是不一样的？同理继续论证，4 个6 呢？3 个7 呢？

完善结论：加数相同的加法算式的和，只与加数本身和加数的个数有关。

【思考：经历数学探究，严谨推理，得到有关乘法意义的重要结论——加数相同的加法算式的和，只与加数本身和加数的个数有关。为后续乘法自然地产生做好铺垫。同时学习体会数学探究中观察、比较、分析与试验等数学方法。】

三、运用结论，引出乘法

师：得到了一个非常重要的结论，可是这个结论有什么用呢？

生：可以让我们读2+2+2+2+2=10 这样的加法算式时，不用再读二加二加二加二……了，直接读五个二相加（连加）就可以。

师：这个读法也太方便了！既然读法（读法两个字加重音）可以变得如此简洁，那么——

生1：有没有可能写法也变简洁一些呢？

生2：可以写成2+……+2（5个2）。

师：简洁了些，还有没有更简洁的方式？（逐步引导出乘法算式）

生3：5×2=10。

（请该学生解释5×2=10 表示的含义，并进行相应的板书）

师：为什么中间的运算符号要用“×”而不是用“+”，原本不是加法算式吗？

生：再用“+”就变成5+2 了。

师：是啊！如果再用“+”就变成5+2 了，与5 个2 连加的意义不相符，怎么办？

生：为了不把“5+2 的和”与“5个2 连加的和”混淆，所以，需要创造一个新的运算符号“×”来表示“几个几连加的和”的意思。

师：太棒啦！创造一个新的运算符号，真是一种新奇的方式，把相同加数连加算式书写变简单的同时，也表达出了相应的含义。谁还能重复刚刚这位同学的说法？

（再请2～3 位学生表述，让全体同学一起感悟新的运算符号“×”产生的必要性。及时进行乘法算式的读、写以及各部分名称的教学，并进行相应的板书）

板书：

【思考：通过“加数相同的加法算式的和，只与加数本身和加数的个数有关”这一重要结论，逐步引导出乘法。真实再现乘法为什么是由加数和加数的个数这两个数相乘组成。再通过乘法与加法的对比，感受创造“×”及乘法这一种符合数学规律的运算的必要性。培养符号意识，初步体会符号的使用是数学表达和数学思考的重要形式。同时，有加法的知识做支撑，趁热打铁进行乘法算式的读、写以及各部分名称及含义的教学，则水到渠成。】

四、在巩固中深化乘法的意义

练习一：把下面的加法算式改写成乘法算式。6＋6＋6＋6＝24 （ ）个（ ）

乘法算式：_______________4＋4＋4＋4＋4＋4＝24 （ ）个（ ）

乘法算式：_______________

练习二：根据图示写出加法算式和乘法算式。

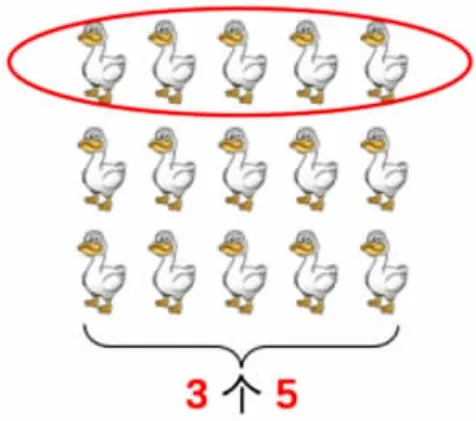
加法算式：_______________

乘法算式：_______________

加法算式：_______________

乘法算式：_______________

师：大家对于相同加数连加的求和运算，可以变成新的运算——乘法，理解和掌握得不错！仔细观察练习二，有什么特点与发现？

生：3×5＝15 与5×3＝15，只是乘数交换了位置，积不变（也就是总和没变），从意义上理解，区别是，一个横着看图，横着数，然后连加，另一个是竖着看图，竖着数，然后连加。

师：真不错！既然如此，刚刚练习一中的4 个6 连加与6 个4连加的题目，也只是乘数交换了位置，积不变（也就是总和没变）。是否可以像练习二一样，也变成一幅图，只是横着看和竖着看的区别呢？

（学生将4×6 与6×4 的意义抽象成数学化的图示表征——矩阵模型）

师：乘法运算这样的特点，在什么运算中也遇见过？

生：加法运算中。比如，4＋6 和6＋4，结果都等于10。

师：你真棒！迅速地联想到了一年级学习加法时，一幅图可以列出两道加法算式。看来，乘法和加法真不愧是一对“好朋友”呢！

【思考：乘法的本质意义是几个几连加，练习一借助相同加数连加的加法算式与乘法算式之间的转换，可以巩固学生对于乘法意义的理解与掌握。练习二借助数形结合的方式，不仅巩固对乘法意义的理解，更是帮助学生拓宽了对乘法的认知。同时这一特征还可以与已经学习的加法相关联，对比总结出乘法与加法都有类似的特征（交换位置，结果不变），不仅为以后要学习的交换律做好铺垫，还沟通了乘法与加法间的内在联系，使学生的知识结构更加完整。】

五、总结与发散

师：今天学习了什么？我们是怎样学习的？大家还有什么疑惑？

（学生回答略）

师：通过今天的学习，大家发现乘法是解决相同加数连加这类问题的简便、好用的方法。难道只有相同加数这样的算式，才有简便好用的计算方法吗？在一年级就学过许许多多的数字规律，数字相同只是其中最普通的一种。例如：1、3、5、7、9……这样的数字组成连加算式，有没有简便运算方法？或者有没有可以让乘法运算更加简便的运算方法？或许你可以找到某种规律，并创造出属于你自己的运算符号与方法。

【思考：本课是对乘法的初步认识，但通过数学探究的方式，让学生对于运算的理解，不应仅仅止步于乘法。】