某大型固体发动机T800碳纤维壳体封头结构仿真分析和优化设计①

喻琳峰,任全彬,张爱华,宋学宇

(1.西安航天动力技术研究所,西安 710025;2.航天动力技术研究院,西安 710025)

0 引言

在实际工程应用中,国产T800碳纤维缠绕壳体的力学性能表现往往比不上传统使用的进口T800碳纤维[1-2],甚至有时候仅仅能与进口T700碳纤维持平。特别是壳体封头部位往往在压力未达到设计爆破压强时就会发生破坏,主要原因在于,封头处于不同种类材料的交界处,会出现材料不同,刚性不同,对应力的敏感不同的情况。受压时,由于形成应力的不连续传递,导致形成了局部的应力集中区,从而成为承力薄弱点,并首先发生破坏[3]。同时,壳体的赤道位置处由于环向层的加入形成了几何形状突变,导致了该位置存在较高的应力。在传统设计方法以网格理论为基础的分析计算中,既不考虑基体树脂的作用,也未考虑缠绕层次的工艺影响,更不可能考虑结构内部缺陷以及纤维与基体界面作用的影响。在实际工程中靠近赤道位置和临近金属接头位置的纤维缠绕层的受力较为复杂,容易发生纤维断裂或层间剪切的破坏现象。以上原因最终导致了网格理论对靠近赤道位置和临近金属接头破坏位置的设计和分析都不够准确。因此,应针对T800碳纤维材料的壳体封头使用试验或仿真方法,以达到更为理想的研究效果,并进一步开展优化设计研究。

在以往的封头优化设计研究中,已有较多研究人员对封头结构进行了仿真分析。崔向斌等[4]使用ANSYS软件,建立了带金属接头的纤维缠绕壳体模型,并利用壳体解剖数据实现变截面厚度。计算发现在内压作用下,后封头在距离赤道附近的区域会因为变形协调产生收缩趋势,表现出4个屈曲波形态的内凹变形并判断为壳体封头薄弱区。程勇等[5]使用ANSYS软件,将数值应力分析与复合材料成型工艺相结合,采用三维层合实体单元对壳体模型进行有限元计算,发现由于金属接头刚度远大于复合材料壳体刚度,壳体从金属接头边缘附近的应力、应变水平较高;同时由于赤道前后刚度变化,在封头靠近赤道线处应力、应变水平也较高。PARK等[6]使用非线性有限元分析方法结合ANSYS的APDL语言对壳体的爆破位置进行了预测分析。缑林虎等[7]对椭球封头模型进行了非线性有限元分析,发现应力应变在金属接头附近及接近赤道圆位置变化较大。封头处的沿纤维方向应变是表现封头结构可能发生破坏的重要表征指标,特别是封头靠近赤道位置与金属接头位置可能会发生纤维应变的大范围变化,实际中该位置会因此发生缠绕层的纤维断裂。由此可知,依据封头靠近赤道位置或金属接头附近的最大沿纤维方向应变得到的优化结构较为可靠。

在补强手段方面,王东等[8]分析了纤维纵向缠绕补强、裁剪条形碳布补强和裁剪环形碳布补强三种补强的效果,通过对这三种补强方法完成的壳体进行水压爆破试验,发现采用环形碳布补强对增强壳体后封头强度的效果较高。关云等[9]利用ABAQUS软件建立了包括金属接头、封头补强层、弹性层、缠绕壳体层的壳体模型,通过Python对ABAQUS进行二次开发,构建了精细化的复合材料壳体有限元模型,计算结果表明,采用环向补强壳体的封头内压承载性能和稳定性能明显优于纵向补强方法。

目前壳体封头补强技术主要采用轴向、环向、编织布和封头帽补强方法[10-11],我国对于传统的补强手段应用也比较成熟,但对于封头补强工作研究却基本依托于经验,缺乏基础理论研究作为参考。同时,许多精细化仿真工作仅针对小规模的壳体结构展开,对工程应用缺乏有效的指导作用,基于理论的研究很难与工程实际很好地结合起来。实验表明,在目前工程中把以往的封头补强经验应用于国产碳纤维时,往往没有办法达到预期的效果,由于在实际工程中,国产碳纤维的高模量、高强度性能无法很好地体现出来,甚至有时还出现了性能降低的现象,因此有必要对补强结构进行系统化的优化设计,丰富对国产碳纤维缠绕层参数对封头结构性能影响的认识。而近几年的文献显示,国外对于壳体封头的结构优化已经倾向于在设计阶段就对完整壳体封头进行优化设计[12-13],这是如今国内研究所欠缺的。因此,有必要系统地基于工程实际和计算基础,对壳体进行精细化建模,然后进行合理优化设计,以形成一套系统的针对碳纤维缠绕壳体封头优化设计体系。

本文以某T800碳纤维缠绕壳体后封头为研究对象,在设计阶段引入壳体封头的优化设计。首先通过试验及仿真手段确定优化目标,然后基于辅助代理模型设计一套后封头优化设计方法,最后对优化结果进行评估,形成一套完整的壳体设计方法,并论述未来进一步的研究方向,为今后的大型碳纤维缠绕壳体封头设计工作提供参考。

1 复合材料壳体模型建立与验证

1.1 复合材料壳体水压爆破试验

根据固体火箭发动机工程需求,本文采用某T800碳纤维缠绕壳体后封头模型,模型由金属接头、橡胶垫片组成。封头型面为椭球比1.7的椭圆封头,后极孔半径为390 mm,半筒身长度为790 mm。壳体采用T800环氧树脂纱带缠绕成型,纱带宽度为18 mm,单层厚度为0.36 mm,筒身缠绕角α=18°,由于壳体为非等极孔结构,故采用非测地线缠绕成型,壳体的缠绕角成型公式为[14-15]

(1)

式中R为纵向缠绕层到中心轴线的径向距离;R0为过渡点到中心轴线的径向距离;Rtl为封头和筒身过度段半径;θtl为筒身段纵向缠绕层缠绕角;δ为测地线和非测地线缠绕角之间的偏差程度。

当δ=0时,式(1)为测地线缠绕角计算式。

非测地线缠绕成型下的纵向缠绕层厚度模型公式如下[14-15]:

(2)

式中ttl为筒身段纵向缠绕层厚度;θr为对应不同平行圆半径的缠绕角;rtl为赤道圆半径;r0为纵向缠绕层转向的半径;r为封头上任意一点对应的平行圆的半径;BW为纱带宽度。

对复合材料壳体进行缠绕成型和水压爆破后结果如图1和表1所示。可以看出,在16 MPa的内压载荷下,爆破在封头靠近赤道部位发生,筒身段的环向应变在0.011 8左右。

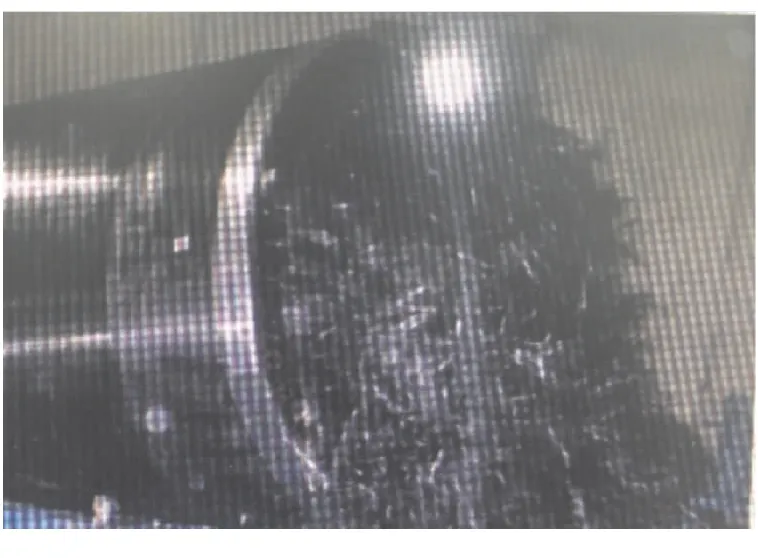
图1 未补强壳体水压爆破后封头形貌Fig.1 Hydrostatic burst tests of composite cases without reinforcement

表1 未补强壳体水压爆破试验结果Table 1 Results of hydrostatic burst tests of composite cases without reinforcement

1.2 复合材料壳体有限元模型建立

依托ABAQUS仿真软件建立该壳体后封头模型,模型包含金属接头、堵盖、橡胶垫片以及T800碳纤维缠绕层四部分。金属接头材料使用铝金属,垫片材料采用橡胶,堵盖采用钢材料,金属接头、垫片和堵盖的材料参数如表2所示,复合材料参数如表3所示。

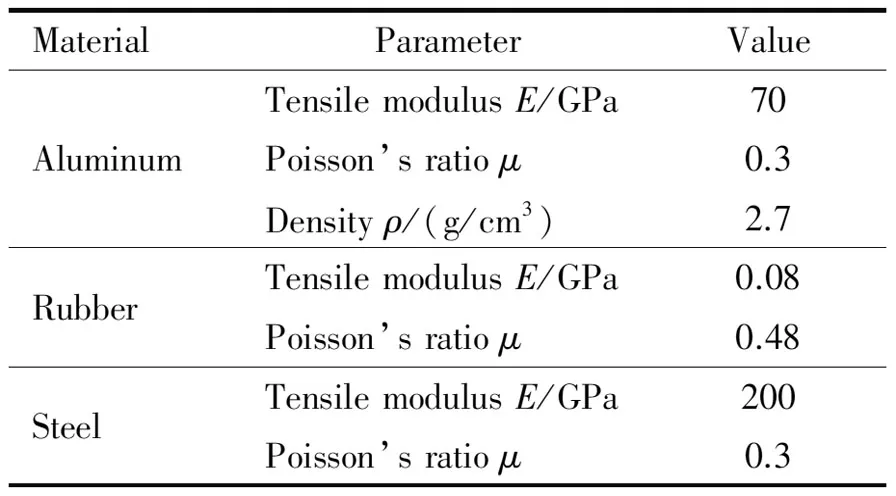
表2 接头、垫片及堵盖材料属性Table 2 Material properties of joint,gasket and cover

表3 T800碳纤维/环氧树脂复合材料性能参数Table 3 Performance parameters of T800 carbon fiber/ epoxy resin composites

根据上述材料,使用Python对ABAQUS进行二次开发建立精细化壳体模型,如图2所示,并开展数值仿真,有限模型由堵盖、金属接头、橡胶垫片和纤维缠绕层组成。为实现封头有限元模型连续变厚度变角度,本文在ABAQUS中通过细化单元,获得足够的单元数量,通过编写Python 脚本,将缠绕角以1°的角度增量进行离散,生成正负角度,并将其赋予封头不同位置的单元,这样做既可实现角度连续,又能达到封头正负铺层的效果,纵向缠绕层铺层角度变化如图3所示。缠绕层分为11层纵向层和20层环向层,各缠绕层的具体工艺参数如表4所示。

图2 碳纤维缠绕壳体后封头模型Fig.2 Aft-dome of carbon fiber wound case

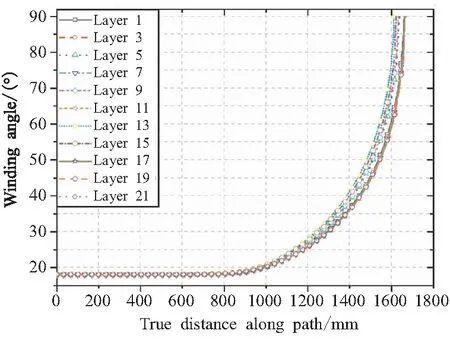
图3 缠绕角变化曲线Fig.3 Winding angle curves

表4 缠绕层工艺参数Table 4 Winding layer process parameters mm

为减少计算量,采用壳体全模型的1/36仿真分析,堵盖、金属接头和橡胶垫片均采用混杂单元,其中堵盖包含C3D8R缩减积分单元2360个,C3D6实体单元65个;橡胶垫片中C3D8RH单元60个,C3D6单元6个;金属接头含C3D8R单元1460个,C3D6单元32个。复合材料层采用C3D8实体单元,个数为232 992个。

壳体载荷约束根据水压爆破试验添加,对壳体模型内面施加15 MPa的压力,由于采用1/60模型,模型截面施加循环对称约束,并在底面施加对称约束(图4(a))。金属接头和堵盖之间、金属接头与垫片、垫片与缠绕层间施加绑定约束(图4(b)),金属接头侧面与堵盖侧面、接头与缠绕层头部之间采用滑动摩擦约束,摩擦系数设为0.1(图4(c)、(d))。

1.3 有限元模型计算结果分析及验证

对于未补强优化的壳体模型的计算变形结果如图5所示。由仿真结果可知,在15 MPa的内压环境下,封头处会产生较大的位移变化,壳体的变形主要集中在最外层缠绕层的临近接头、垫片与封头靠近赤道位置附近,如图6、图7所示,这与之前的分析结果一致。

图5 后封头位移云图Fig.5 Displacement contour of the aft dome

图6 金属接头附近应变云图Fig.6 Strain contour of metal joint of outermost winding layer

图7 赤道位置附近应变云图Fig.7 Strain contour of equatorial position of outermost winding layer

提取筒身段的环向应变如图8所示,可见在筒身内壁会达到最大的环向应变,最大应变为0.011 1,与实验结果差5.9%,且由于仿真设计爆破压强为15 MPa,因此结果在误差范围之中。由此可知,仿真结果是精确可信的。

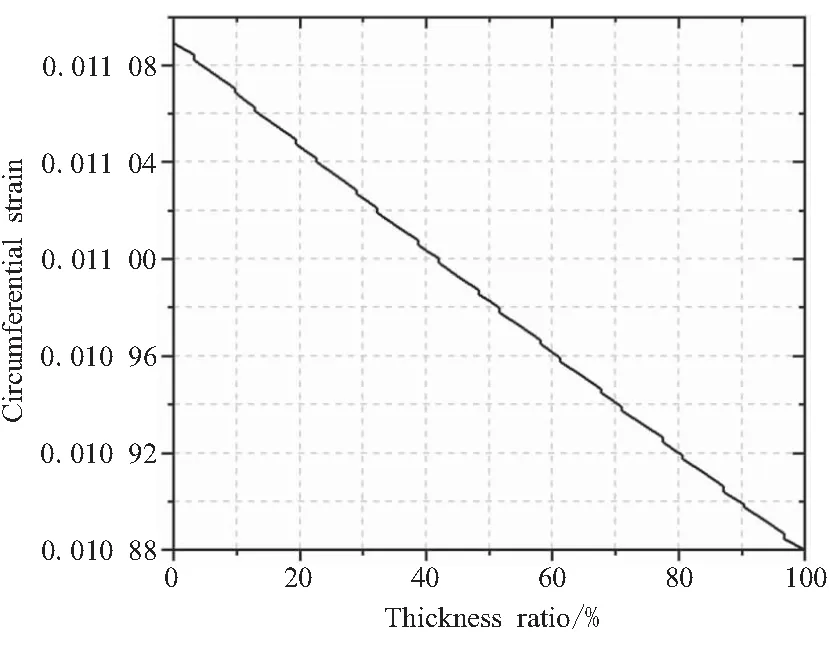
图8 筒身段环向应变Fig.8 Toroidal strain curve of barrel

提取各纵向纤维层的剪切应力变化情况,如图9所示。可以看出,最外层缠绕层在封头靠近赤道位置和接头附近可以达到最大的700 MPa和350 MPa,其中又以封头靠近赤道位置的应力变化情况最为复杂,数值波动也最为剧烈,由此可知,封头靠近赤道位置很可能发生剪切破坏,有必要对赤道位置进行进一步的分析。

图9 纵向缠绕层剪切应力Fig.9 Shear stress of longitudinal winding layer

接着提取各纵向纤维层的沿纤维方向应变云图后可以发现,在封头赤道附近存在最大的沿纤维方向应变,如图10所示,且最大应变会第1或第11层纵向纤维层出现,根据应变曲线图(如图11、图12所示)可以看出,排除缠绕层头部的计算偏差因素后,最大沿纤维方向应变会在封头靠近赤道处达到0.016 5,而筒身处的纤维方向模量却只有0.01,封头靠近赤道位置处的纤维应变相比筒身处增加了65%。在实际工程中,一般情况下壳体发生爆破时,封头靠近赤道位置的最大沿纤维方向应变在0.013左右。因此,在15 MPa的内压环境下,该位置极有可能发生纤维断裂破坏,此处将作为本文接下来的主要研究位置进行研究。

图10 纵向缠绕层赤道附近纤维应变云图Fig.10 Fiber strain near equator of helical winding layer

图11 第1、11层纵向纤维应变Fig.11 Fiber strain in helical layers 1 and 11

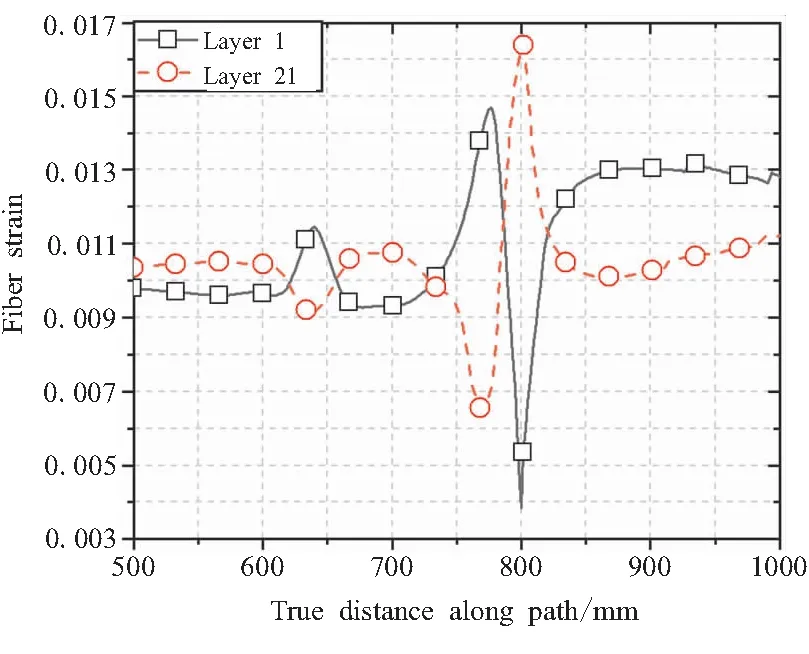
图12 封头赤道位置纤维应变Fig.12 Fiber strain at equatorial position of dome

根据分析结果可以得出结论,该壳体结构在封头靠近赤道位置存在较为复杂的变形情况,如图13所示,因其处于封头末端,纱带间堆叠较少,因此缠绕层厚度较薄,同时该位置处在筒身段环向缠绕层起始位置附近,存在厚度突变现象,此位置的受力情况为多种应力耦合的结果,存在复杂的应力应变变化,且数值波动范围较大。因此,该位置应成为最重点的研究与优化设计位置。各缠绕层中又以最外层纵向缠绕层的应力应变情况最为复杂、多变,因此也最容易首先发生破坏。

图13 封头近赤道位置变形情况Fig.13 Deformation near equatorial position of dome

根据祖磊等[16]对壳体封头结构的损伤失效分析可知,纵向纤维断裂失效为壳体爆破失效的主要以及最早发生的失效模式,也是封头靠近赤道位置的主要失效形式。因此,本文的主要设计优化目标为最外缠绕层封头靠近赤道位置的最大纤维应变。

2 结果与讨论

结构优化设计是从多个设计方案选择最优的设计方法,以数学理论为基础,根据结构设计需要满足的性能指标,设定约束条件,选择设计优化变量,建立目标函数,寻找最优解。由于现代大多数的工程实际优化问题都比较复杂,一般仿真软件对单个模型的计算时间会达到几分钟甚至几天,传统的仿真优化设计使用有限元软件对大量样本进行受内压变形模拟,再联合优化算法对结构进行优化设计的方法明显不可行。

为了降低计算时间,减轻计算负担,本文采用基于近似模型的优化方法,即在优化前进行实验设计并构建代理模型[17]。本文的优化设计过程主要分为如下几个步骤:

(1)确定优化目标和设计参数。本文以最大沿纤维方向应变为优化目标,根据不同缠绕层退移半径、带宽、补强位置为设计参数建立如下优化模型:

(3)

式中F(Xi)为最大纤维应力目标函数;S、t、Rb为补强优化参数设计变量,分别为退移半径、带宽、补强起始半径。

(2)初始化种群数量,同时根据不同参数组合为单个种群的染色体。

(3)建立有限元模型样本,求解有限元模型,输出封头靠近赤道位置最大纤维应变。

(4)补强参数寻优,通过基因选择、杂交、变异,求解适应度函数,并判断最优解是否满足目标要求,若不满足则再次循环新一代,返回基因选择步骤,同时修改有限元模型的参数变量值;若最优解满足目标要求,则输出最优的补强角度和补强层数。

根据国产T800碳纤维壳体的缠绕方式、补强铺层位置等变化影响壳体力学性能,将设计变量定为退移半径、带宽、补强起始半径三个变量,补强材料选取T800碳纤维补强层,共两层补强带前后半径200 mm,每层补强厚度为0.36 mm,分别设立在第4、第5层纵向缠绕层与第5、第6缠绕层之间,即位于纵向缠绕层中部。各参数取值范围如表5所示。其中,纤维的退移、纱带宽度和补强层的起始半径都是设计阶段的重要可设计参数。缠绕层退移会引起封头型面缠绕角和几何形状的变化,带宽涉及缠绕工艺的变化影响几何形状发生改变,补强层的位置会直接影响封头模量和厚度。以上三种参数都可以对以最大纤维应变为目标函数的优化设计起到至关重要的作用。

表5 优化变量参数取值范围Table 5 Optimization variable parameter value range

实验设计采用空间填充实验设计,采样方法为Latin Hypercube Sampling(LHS)采样方法,这样做的好处是可以以较高的离散度在整个设计空间中进行随机采样,由于LHS采样方法属于分层采样,可以使设计空间中的所有区域都会被采样到,确保采样点对设计空间的全面覆盖。而且从方法产生的样本也非常适用于神经网络的拟合计算[18]。

使用LHS采样方法采样50个采样点后依据神经网络算法构建本文的代理模型,相较于其他模型,神经网络对于复杂非线性问题具有更强的逼近能力[19,20]。构建的神经网络系统结构为3-3-1,即输入层3个神经元对应于系统的3个输入变量,隐藏层设3个神经元,仅有的单个输出对应于输出层的一个神经元。训练结果如图14、图15所示。可以看出,网络输出与训练集目标的相关系数为0.999(最佳值为1),网络综合性能分析相关系数为0.969。由此可见,该训练模型较好的实现了对训练样本集的拟合。

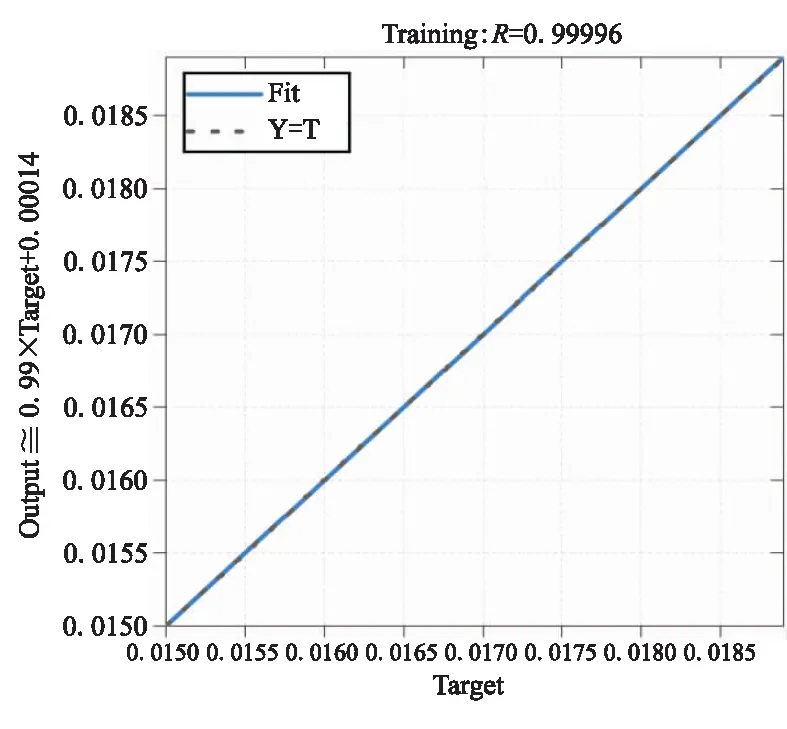
图14 网络输出-训练样本线性回归分析Fig.14 Network output-training sample linear regression analysis

图15 综合网络性能曲线Fig.15 Integrated network performance curves

在建立代理模型之后,可对三个优化变量进行灵敏度分析。图16～图18给出了纤维退移距离、纱带宽度和补强起始半径对最大沿纤维方向应变的响应曲线。

图16 退移层退移距离对目标函数的影响Fig.16 Influence curve of backsliding distance of backsliding layer on objective function

图17 纱带宽度对目标函数的影响Fig.17 Influence curve of yarn bandwidth on objective function

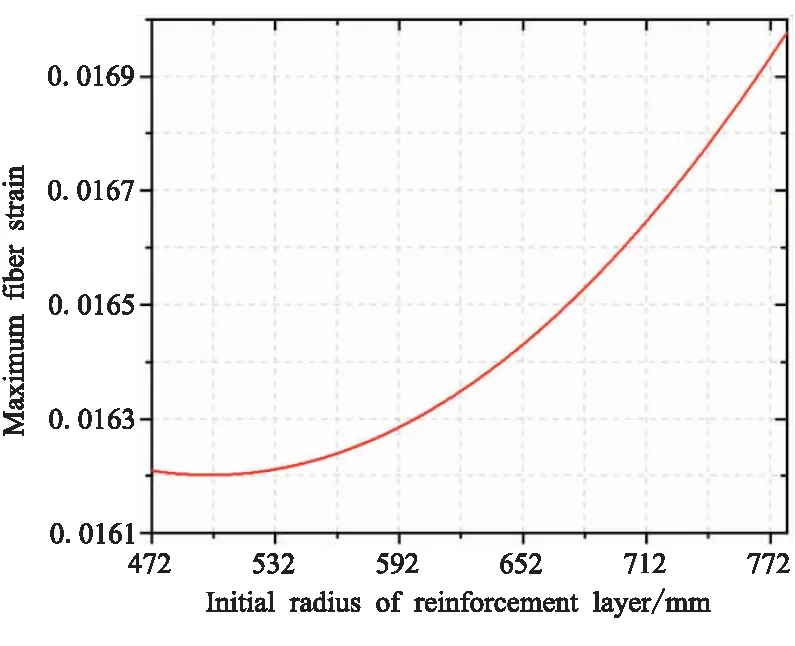
图18 补强层起始半径对目标函数的影响Fig.18 Influence curve of initial radius of reinforcement layer on objective function

相对于原结构,最大纤维应变随退移距离的变大而呈线性下降,下降范围在0.017 2～0.015 9,即退移纵向纤维层的退移量越大,封头靠近赤道处的纤维应变就越小。由数据范围大幅度变化可见,退移距离参数对最大纤维应变的影响是不可忽视的。最大纤维应变随纱带宽度和补强层起始半径增长呈现非线性的先下降后上升趋势,存在最佳值,但在其余参数没有变化的情况下,与原未补强结构相比,对最大纤维应变的影响不是特别明显,但是过大或过小的纱带宽度、过大的补强起始半径位置对封头靠近赤道位置沿纤维方向应变会有不利影响。综上所述,对封头靠近赤道处的沿纤维方向应变影响最大且最直接的变量是封头近赤道位置的型面几何形状复杂程度,同时可知,封头靠近赤道处应有较为复杂的变形和受力情况,有必要对该位置进行优化研究。

应用遗传算法对所构建的神经网络代理模型进行优化搜索,获取目标函数的极小值点。算法基于Matlab软件平台,流程包含选择、杂交和特征突变三个算法[21],如图19所示。

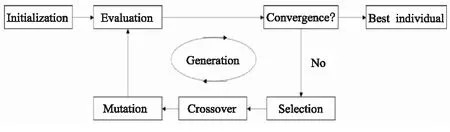
图19 遗传算法流程图Fig.19 Genetic algorithm flow char

算法最终给出具有最佳适应性个体的各项参数及适应值,如表6所示,可以看出退移量及纱带宽度均已达到最大设计变量,补强层则处于后封头中间位置。由于退移量为影响优化目标的主要影响参数,因此其最优取值与灵敏度分析中所得到的结论相同,接近最大取值。而由于退移量的增大,影响了后封头型面的缠绕角变化规律以及封头厚度,采取灵敏度分析中纱带宽度和补强层位置取值可能会导致封头型面变形产生不利变化,再加上这两个变量对优化目标的影响要小于退移层退移距离的影响,考虑到三个变量的联合作用既相互影响,因此最终优化取值与灵敏度分析得出的最佳取值不同。

表6 最佳适应值参数Table 6 Optimum fitness parameters

由于优化算法的函数值基于代理模型得出,这导致所求得的目标函数值只是近似解,因此有必要再次对优化结果所得参数进行仿真计算,以获取优化设计结构所对应的目标函数真值,从而对优化设计结果进行评估。仿真后第1、21层纵向缠绕层的沿纤维方向应变曲线如图20所示。可知,仿真后得到的最大沿纤维方向应变仿真值为0.015 8,与代理模型预测值之间的误差为0.63%。这说明构建的代理模型的拟合精度较高,结果的可靠性基本可以保证。与未优化结构进行对比可知,优化结构的最大纤维应变减小了4.2%。

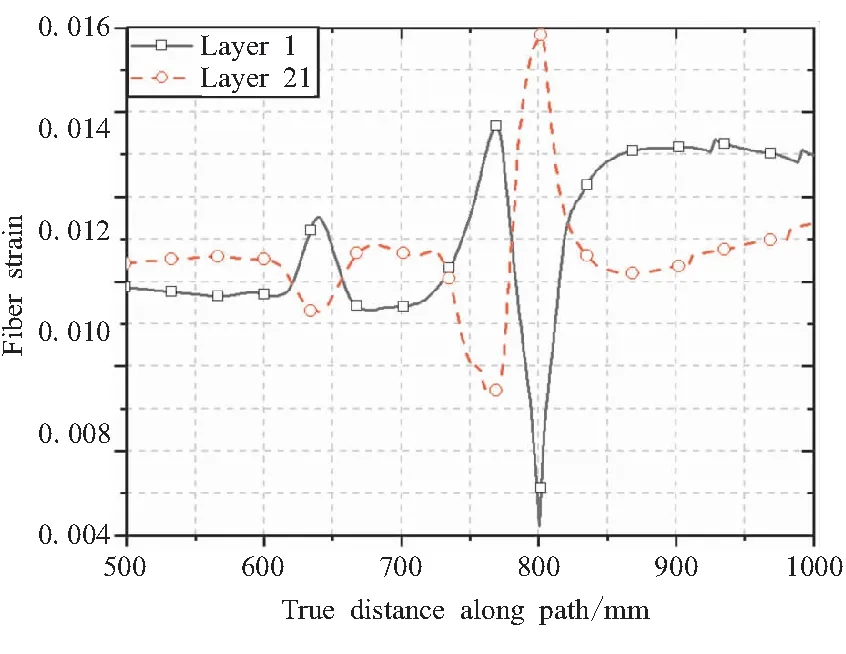
图20 优化模型封头靠近赤道处纤维应变Fig.20 Fiber strain at the equator of the optimized model dome

3 结论

(1)根据所建的精细化仿真模型,最大沿纤维方向应变出现于最外层纵向缠绕层的封头靠近赤道处。此外,靠近金属接头处特别是与垫片接近处的最内、外层缠绕层也会存在较大的纤维应变变化与剪切应变。对比水压爆破试验可知,在最外层的近金属接头部位、封头靠近赤道部位很容易发生纤维断裂破坏,在最内层的靠近金属接头部位出现剪切破坏的可能性较高。

(2)通过构建代理模型简化了大量的仿真计算时间,LHS的实验设计方法做到了对材料空间的全面覆盖效果,拟合后的相关系数可以达到0.99,目标函数预测值与仿真值之间的误差为0.63%。优化变量中,退移层退移距离对目标函数影响显著且呈线性关系;纱带宽度和补强层设置位置对目标函数影响存在最佳值,不当取值会对目标函数起到恶劣影响。

(3)基于遗传算法对结构进行了优化设计,获得了以缓解壳体封头最大纤维应变为导向的最优壳体封头设计方案,其中砂带宽度为25.96 mm,退移层退移距离为19.98 mm,补强层的起始半径为579.38 mm处,优化后壳体封头的最大沿纤维方向应变为0.015 8,对比原结构减小了4.2%。

(4)对于其他模型,封头于接头肩部位置处的最大顺纤维应变可考虑与最大纤维应变同时作为优化目标进行多目标优化设计,这样可以兼顾封头的其他重点薄弱位置,同时可以考虑以封头最大应力作为优化对象进行优化设计。该优化设计与损伤失效分析可作为后续的研究内容的指导方向。