一种考虑颗粒表面形貌的固体推进剂细观模型构建方法①

2023-08-30蒋秋梅张镇国

固体火箭技术 2023年4期

袁嵩,蒋秋梅,张镇国*,翁琳

(1.海军装备部,西安 710025;2.西安航天动力技术研究所,固体推进全国重点实验室,西安 710025;3.上海工程技术大学城市轨道交通学院,上海 201620)

0 引言

固体推进剂是固体发动机的动力之源,其能量特性直接关系到发动机乃至整弹的性能水平,并且其成型药柱的结构完整性也直接关系到发动机乃至整弹的工作成败[1]。当前,火箭总体对固体发动机的精细化设计要求越来越高,固体推进剂药柱的细观仿真分析已成为研究热点之一。固体推进剂通常由金属燃料Al颗粒、氧化剂AP颗粒、高分子粘合剂基体及防老剂、键合剂等组成,是典型的颗粒增强复合材料,构建能够有效表征推进剂细观结构特征的代表体积单元(Representative Volume Element,RVE)是进行细观仿真分析的前提和基础[2-3]。

目前,细观结构模型的构建主要基于几何拓扑方法和CT(Computed Tomography)扫描重构技术。几何拓扑方法方面,LUBACHEVSKY等[4]最早研究了随机颗粒堆积的几何特性及最密堆积方法,对后来建立随机细观模型的研究起到奠基性作用。KOCHEVETS等[5-6]进一步发展了LUBACHEVSKY的方法,并最终建立了较为系统的分子动力学算法(MD:Molecular Dynamics)用于颗粒复合材料RVE模型生成。SEGURADO等[7]发展了随机序列吸附(RSA:Random Sequential Adsorption)方法,并用于颗粒复合材料的细观界面“脱湿”研究。目前,大多数学者主要采用MD方法或RSA方法建立推进剂的细观模型,开展推进剂的界面“脱湿”、损伤演化等研究[8-11]。由于三维的RVE模型计算量大且收敛难度高,以往大多数研究均以二维模型为主,采用三维特别是考虑表面特征的非球形三维细观模型的仿真研究刚刚起步[12-14]。此外,也有学者采用μCT对固体推进剂进行了扫描,重建得到了试样的三维结构,但是受限于μCT扫描仪器精度,未能分辨出3.5 μm以下的颗粒[15-17]。综合来看,采用μCT扫描重构技术可以获取固体推进剂内部的真实结构,但是重构模型的精度受限于μCT扫描设备的精度及重构算法的准确性。目前,采用几何拓扑方法开展固体推进剂的细观研究仍是主流,但当前MD算法和RSA算法仅可以构建二维圆形或三维球形RVE模型,且在固体颗粒填充比较高时(一般≥70%),模型生成效率较低,尚缺乏高体积含量非球型RVE模型生成算法方面的研究。

本文基于Voronoi结构,通过Python对Abaqus二次开发,构建一种考虑颗粒复杂形貌的固体推进剂细观模型构建方法,可快速生成圆形/球形、多边形/凸多面体二/三维细观模型,多边形/凸多面体状态的填充比理论上可以达到1,丰富推进剂细观模型构建方法体系。

1 基于Voronoi结构的复杂形貌颗粒RVE模型生成算法

1.1 Voronoi结构介绍

维诺结构(Voronoi structure)又叫狄利克雷镶嵌(Dirichlet tessellation),广泛应用在几何学、地理学、晶体学等学科[18]。典型的Voronoi结构如图1所示。图中,红色点为种子点,蓝色线条为Delaunay三角网,红色线条为Voronoi结构。

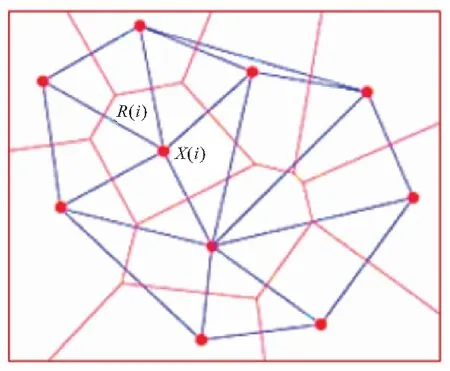
图1 Voronoi结构构造示意图Fig.1 Schematic diagram of Voronoi structure

目前已有很多开源工具可以很方便地生成二维或三维Voronoi结构,由于Voronoi结构的每个晶胞都具有外凸多边形的特点,在固体推进剂细观结构建模中,可以将Voronoi结构离散之后,通过对单个晶胞进行离散、缩放等操作,建立具有复杂形貌的高填充比推进剂RVE模型。

1.2 多边形/凸多面体颗粒RVE模型生成算法

基于Voronoi结构,实现高填充比的多边形/凸多面体颗粒RVE模型的具体流程如图2所示。

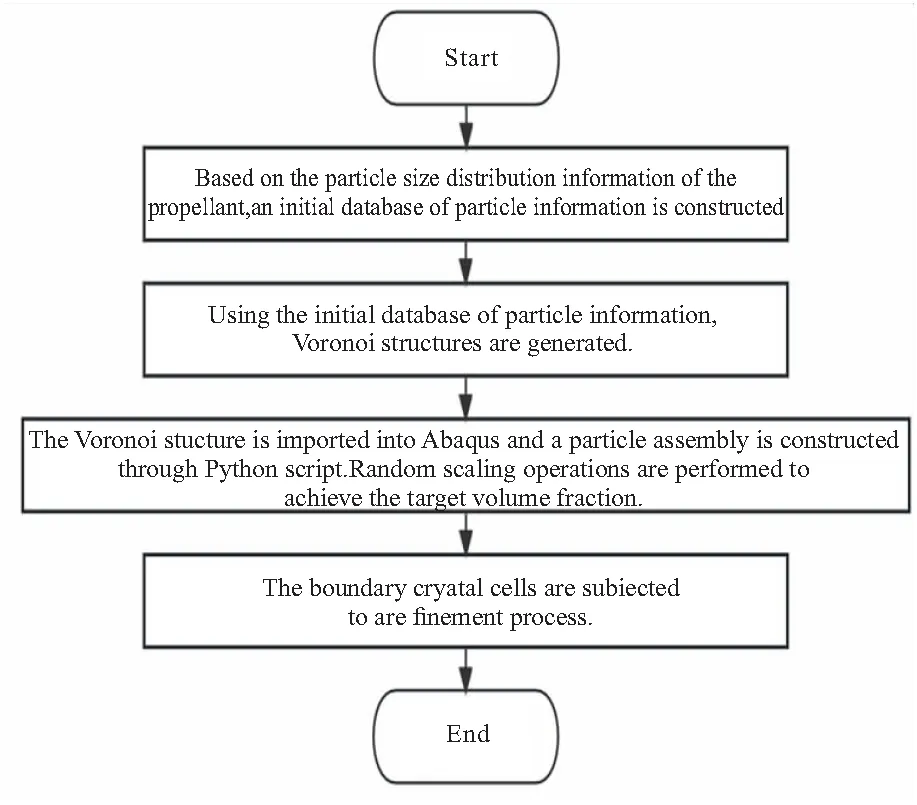
图2 基于Voronoi结构构造多边形/凸多面体颗粒RVE模型流程图Fig.2 Flow chart of construcing polygonal/convex polyhedral particle RVE model based on Voronoi structure

1.2.1 初始颗粒信息库生成

目前推进剂细观分析主要考虑AP、Al颗粒。AP颗粒一般有粗粒径(平均粒径约150 μm)和细粒径(平均粒径约20 μm)两种规格;Al颗粒平均粒径约20 μm,每个规格的颗粒实际粒径均服从正态分布。对于AP颗粒,其分布可以表示为

(1)

对于Al颗粒,其分布为

(2)

则根据推进剂配方规定的具体体积分数,按照式(1)和式(2)可以分别生成每个组分的颗粒数量,每种组分的颗粒数量、组分分布共同组成初始颗粒信息库。

1.2.2 Voronoi结构生成

目前已有很多开源工具(Neper、Python Scipy等)可以方便地生成服从一定分布的Voronoi结构,本文将初始颗粒信息库及RVE模型边界尺寸作为输入,采用成熟开源软件Neper生成周期性Voronoi结构,其总体积等于RVE的体积,如图3所示。Voronoi结构的节点Vi的坐标 (xi,yi,zi)、面Fj几何结构(组成面的节点,Vj1,Vj2,Vj3,…)、晶胞Ck的几何结构(组成晶胞的面,Fk1,Fk2,Fk3,…),可以导出作为下一步操作的输入数据,其中i、j、k分别为节点、面和胞元编号。

图3 采用Neper生成的典型Voronoi结构Fig.3 Typical Voronoi structure generated by Neper

1.2.3 目标RVE生成

采用Python语言编写程序调用Abaqus软件中的几何模块功能,根据Neper的几何输出文件(.ply文件),按照点-线-面-体之间的拓扑关系,在Abaqus中生成颗粒的几何模型,基本过程如图4所示。

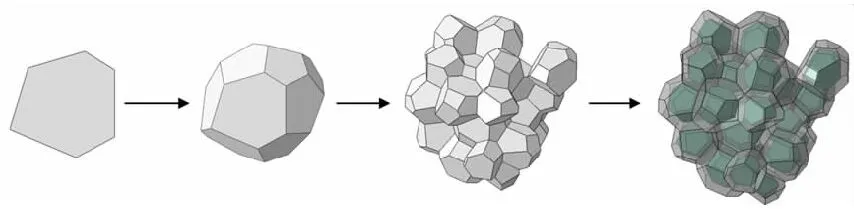
图4 Abaqus中颗粒构造过程Fig.4 Process of constructing particles in Abaqus

采用Python语言编写导入ply文件的接口程序,主要步骤如下:

(1)读取ply文件,根据面Fj(j为面编号)包含的点组{Vj1,Vj2,Vj3,…}(其中,j1,j2,j3,…为组成面Fj的点的顺序编号)的坐标,在Abaqus中建立几何点组;用顺序相邻两点以及首尾两点连成线,用封闭的线组生成面部件Fj。

(2)根据单个胞元的面的索引,挑出组成胞元的面部件,在Abaqus的“Assembly”模块里合并生成单个胞元。

(3)重复步骤(2)生成全部胞元。

使用Abaqus提供的内置函数(Abaqus Scripting Reference Guide,7.1.1),可以直接获取每个晶胞的体积,然后计算各个组分对应的晶胞总体积分数Vf(i),然后根据各组分目标体积分数VfD(i),按照式(3)计算各组分的平均缩放系数Zf(i):

(3)

按照平均缩放系数对各晶胞进行缩放,各组分的实际体积分数已经达到目标体积分数值,但为了增加颗粒间缩放间距的随机性,对每个组分的每个具体晶胞,采用如式(4)所示的随机缩放系数进行缩放操作。

(4)

式中Zf(i,j)为第i个组分的第j个具体晶胞;random(0.8,1.2)为0.8～1.2之间的随机数,随机数产生的范围可以根据实际情况进行微调,但需确保每个Zf(i,j)具体值小于1。

采用式(4)进行随机缩放操作后,再次计算更新各组分对应的晶胞总体积分数Vf(i),然后按照式(3)执行一次缩放操作对体积含量进行修正,即可得到RVE模型中的目标颗粒。

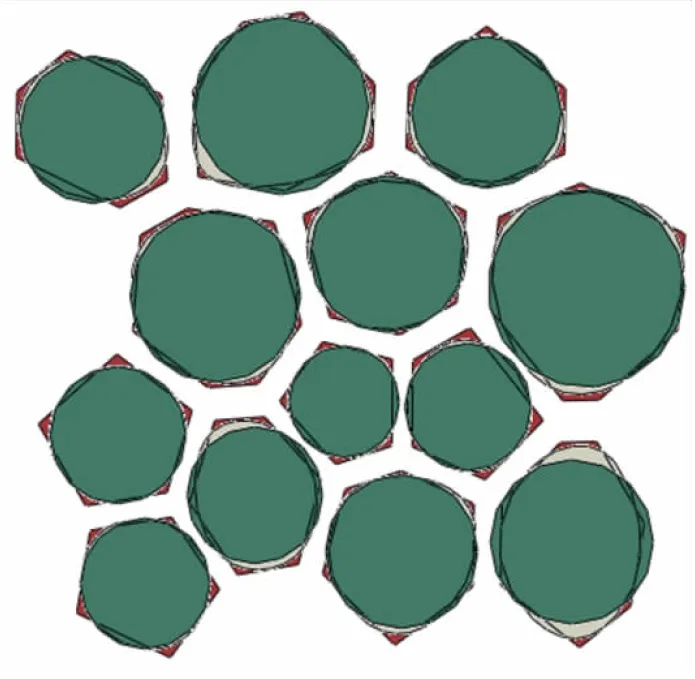
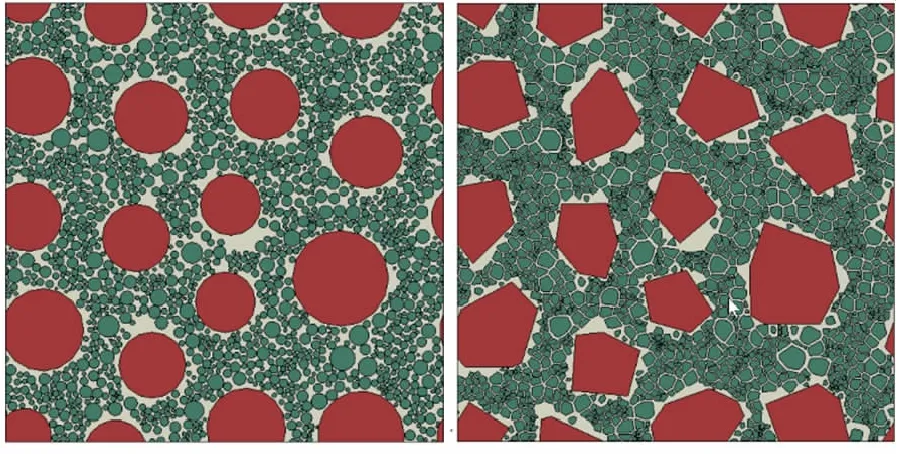
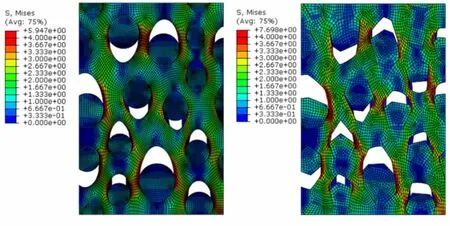
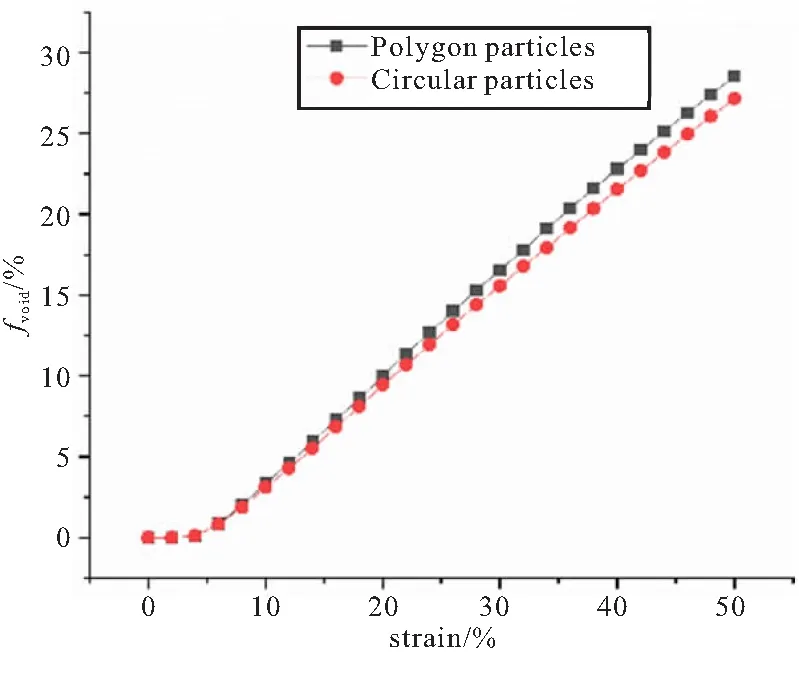
将具有周期性的颗粒进行阵列,并用RVE模型的边界在颗粒中进行随机截取,可以得到具有周期性的RVE模型。但是模型边界处的颗粒会被切开,可能存在很细小的颗粒结构,影响高质量网格的划分,并可能最终影响模型的收敛性。为了尽可能减少RVE模型边界处颗粒的细碎程度,编写自动搜索程序,以模型边界尺寸的1/n(建议10

图5 RVE模型边界颗粒精细化处理示意图Fig.5 Schematic diagram of fine treatment of boundary particles in RVE model

1.3 多边形/凸多面体颗粒RVE模型生成算法

基于Voronoi结构也可以生成圆形/球形颗粒的RVE模型,按照图2所示流程和式(4)生成多边形/凸多面体颗粒RVE模型后,提取每个晶胞颗粒的质心坐标及其面积(或体积),然后在该质心位置建立具有相同面积的圆或相同体积的球,如图6所示。Neper提供“sphericity”参数,可以控制多边形/多面体的球度。当球度较高时,通过多边形/多面体生成同分布圆形/球形颗粒一般不会出现干涉。但是体积分数较高时,为防止干涉产生,在依次建立颗粒的时候,对新加入颗粒j和已有的颗粒(1～i)进行位置判定,新加入颗粒和前面任意一个颗粒之间的质心间离大于两圆(或球)半径之和,如式(5)所示:

(5)

图6 圆形/球形颗粒RVE模型生成过程示意图Fig.6 Schematic diagram of generating RVE model of circular/spherical particles

如果式(5)不满足,则减小新加入的颗粒j的半径,使任意两个颗粒的质心间距大于其半径之和。当所有颗粒均完成干涉检查及处理后,按照式(3)对总体积分数进行修正,以满足目标体积分数要求。

2 RVE模型生成及数值仿真实例

2.1 RVE模型生成实例

按照表1所示HTPB推进剂简化配方,该配方中AP的体积分数为65.5%,其中粗AP颗粒占32.6%,细AP颗粒占32.9%,Al颗粒占10.8%,颗粒总体积分数约为76.3%。

表1 HTPB推进剂典型配方Table 1 Typical formulation of HTPB propellant

参考文献[19]中的二级配粒径范围,本文按照表2所示的粒径分布参数生成细观模型。RVE模型的边长L选为1000 μm。

表2 粒径分布参数Table 2 Particle size distribution parameter μm

按照本文提出的方法在Abaqus中生成的二维圆形和多面体细观模型如图7所示。

(a)Circular particles (b)Polygon particles图7 二维圆形颗粒、多边形颗粒RVE模型(Vf =76.3%)Fig.7 2D RVE model composed of circular particles and polygon particles (Vf =76.3%)

由于生成考虑细小颗粒的三维RVE模型需要较高的计算资源,大多数学者在做具体细观仿真时,首先将小颗粒的Al颗粒、AP颗粒与推进剂基体按照均质化理论进行处理,以均质化之后的基体作为复合基体,颗粒则只考虑大粒径的AP。按照此方法生成只包含32.6%的二维圆形颗粒RVE模型和二维多边形颗粒RVE模型如图8所示,三维圆形颗粒RVE模型和三维多边形颗粒RVE模型如图9所示。

(a)Circular particles (b)Polygon particles图8 二维圆形颗粒、多边形颗粒RVE模型(Vf=32.6%)Fig.8 2D RVE model composed of circular particles and polygon particles (Vf=32.6%)

(a)Circular particles (b)Polygon particles图9 三维圆形颗粒、多边形颗粒RVE模型(Vf=32.6%)Fig.9 3D RVE model composed of circular particles and polygon particles (Vf=32.6%)

2.2 RVE模型数值仿真实例

考虑到实际的计算资源,本文采用2.1节生成的仅包含大粒径AP的三维细观模型进行仿真,验证颗粒形貌对推进剂细观仿真的影响。

在RVE模型施加准周期性边界条件:

其中,L=1000 μm,为RVE模型边长。在y=L面上施加u=500 μm位移载荷,并使用Abaqus中的多点约束方程,使得x=L面上的节点在x方向位移一致,从而x=L面和y=L面在加载过程中保持为平面。

基体采用Neo-Hookean超弹性本构,基体/颗粒界面采用双线性内聚力模型模拟界面分离,参考文献[20]中的复合材基体、AP颗粒及界面的材料参数选取,如表3和表4所示。

表3 材料参数选取Table 3 Material parameter selection

表4 界面参数选取Table 4 Interfacial parameter selection

Abaqus仿真结果如图10所示。可以看到,圆形颗粒RVE模型和多边形RVE模型均可以模拟出推进剂在受载作用下的界面失效特征,但当AP颗粒表面为多边形形貌时,可以看到其颗粒附近应力集中现象更为明显,圆形颗粒附近的最大Mises应力为5.947 MPa,多边形颗粒附近的Mises应力最大达到7.698 MPa。

(a)Circular particles (b)Polygon particles图10 ε=30%时Von Mises应力云图Fig.10 Von Mises stress contours at 30% strain

为了分析两种颗粒形貌状态下的界面“脱湿”损伤发展情况,本文提出针对推进剂二维细观模拟的折算空穴变化率公式,表征界面“脱湿”后形成的空穴,公式如下:

(6)

式中fvoid为模型中cohesive单元的折算空穴变化率;S0为模型初始面积;SDEGi为第i个cohesive单元的折算SDEG损伤值;Si为第i个cohesive单元的面积。

两种颗粒折算空穴变化率对比如图11所示。可以看到,在10%应变之前,两种颗粒的空穴变化率曲线基本重合,表明初始小应变状态下,界面大部分未失效,空穴变化率维持在3%以下,当应变进一步增大,两种颗粒形貌的空穴变化率曲线逐渐分离,且多边形颗粒的空穴变化率略大于圆形颗粒的空穴变化率,说明多边形颗粒的损伤发展要快于圆形颗粒。