基于虚单元法(VEM)的固体推进剂药柱结构完整性分析①

崔 辉 如

(1.陆军工程大学 国防工程学院,南京 210007;2.陆军工程大学 土木工程博士后科研流动站,南京 210007)

0 引言

固体发动机由于结构形式简单,使用方便快捷被广泛用作火箭弹、导弹和探空火箭等的动力装置。药柱结构的完整性分析是发动机安全点火的重要前提。传统的解析方法只能用来处理简单的药柱结构。试验方法,比如采用模拟发动机点火以及冷增压装置等,是最能直观判断药柱结构完整性的手段,但是高昂的试验成本以及有限的可测力学性能参数使其不太可能大规模实现。数值仿真方面,国内的大多数院校和科研机构目前已经可以熟练地运用有限元手段进行自由装填[1]、贴壁浇注式[2]、考虑围压效应[3]以及考虑界面损伤[4-5]的药柱结构完整性分析。此外,有研究人员还针对推进剂的损伤[6]、老化[7]以及粘弹性泊松比特性[8],开展了一些列药柱结构相关的力学响应研究。在利用有限元进行药柱结构完整性分析过程中,几何简化以及网格划分处理几乎占据了绝大部分时间[9]。另一方面,在运输及战备服役阶段,药柱内部会发生裂纹等缺陷,而有限元方法在处理裂纹扩展问题时面临的最大挑战就是裂纹扩展后单元的重构问题[10]。因此,有必要在保证计算精度的前提下,寻求一种对网格形式依赖性较低的药柱结构完整性分析方法。

虚单元法(Virtual element method,VEM)是近10年提出来的一种适用于多边形单元的数值仿真方法[11-13],最显著的特点就是可以不需要形函数的显式表达式,在伽辽金框架下进行双线性以及线性式的计算。正是在处理多边形时不需要设计复杂的形函数表达式,VEM被广泛地用于小变形弹性[14,15]、有限变形[16]以及弹塑性[17-19]问题的求解。国内也有相关研究人员利用VEM开展结构仿真工作。林姗等[20]在VEM的基础上,开展了弹塑性力学问题的应用研究,与传统的有限元方法相比,VEM计算准确高效,网格处理灵活。江巍等[21]使用VEM构建单个块体的位移,发展了基于VEM的非连续变形分析方法的新格式。刘传奇等[22]对VEM的发展、优势、应用等方面开展了全面的综述。尽管VEM还处于起步阶段,但是该方法在诸如非线性问题、接触问题以及裂纹扩展问题上展现出巨大的潜力。目前,国内外尚未有利用VEM进行固体推进剂药柱结构完整性分析研究的报道。

本文首次将VEM方法扩展到固体推进剂药柱的结构完整性分析领域。通过开展粘弹性杆的松弛测试、薄板蠕变测试以及药柱的点火增压分析,验证了VEM在药柱结构完整性分析领域的可行性。本文所有的仿真计算均在课题组自主研发的发动机结构完整性分析软件“CHRMULAR”上实现。

1 VEM方法简介

1.1 二维虚单元空间

假设空间Ω⊂R2被分割成一系列不重合的多边形E的集合Ph,这里的多边形不一定需要凸多边形。对于任意的多边形E,按照逆时针方向标记其顶点Vi,分别为Vi(i=1,…,NV)。类似地,标记多边形的边ei,分别为ei(i=1,…,NV),如图1。

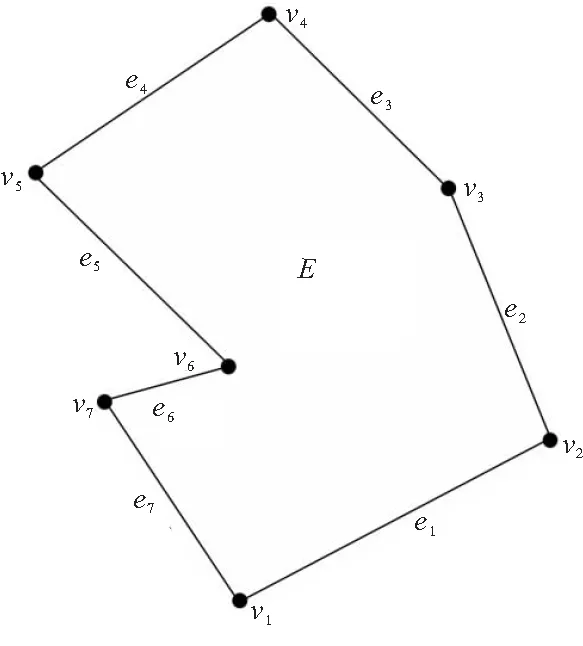
图1 典型多边形EFig.1 Typical polygons E

对于任意的多边形E,定义一个局部虚单元空间Vk(E),该空间包含了所有的k次多项式以及其他一些函数,这些函数在单元边的约束同样也是k次多项式。定义具有以下属性的函数vh∈Vk(E):

(1)vh在单元E的任意边e上是k次多项式;

(2)vh在∂E上是全局连续的;

(3)Δvh在E中是k-2次多项式。

1.2 单元刚度矩阵的计算

对于多边形E,其单元刚度矩阵可以利用拉普拉斯算子进行计算:

(KE)ij=(φi,φj)0,E,i,j=1,…,Ndof

(1)

定义一个从虚单元空间Vk(E)到单元多项式空间Pk(E)的映射算子Π。该算子对于每一个函数vh∈Vk(E)都有如下正交关系:

(pk,(Πvh-vh))0,E=0

for allpk∈Pk(E)

(2)

式中Pk(E)为多边形E上阶次小于等于k的多项式空间;pk属于多项式空间Pk(E)的一个子集。

利用上述算子,可以将基函数φi整理为

φi=Πφi+(1-Π)φi

(3)

那么,单元刚度矩阵可以梳理成

(KE)ij=(Πφi,Πφj)0,E+

((1-Π)φi,(1-Π)φj)0,E+

(Πφi,(1-Π)φj)0,E+

((1-Π)φi,Πφj)0,E

(4)

利用映射算子的性质,上式中的最后两项均为0,那么单元刚度矩阵可以进一步表示为

(KE)ij=(Πφj)0,E+

((1-Π)φi,(1-Π)φj)0,E

(5)

进一步地,单元刚度矩阵可通过计算并简化成

(6)

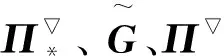
关于辅助矩阵的数值计算,可以参考文献[13]。

2 线粘弹性本构模型

考虑泊松比ν为常数,推进剂线粘弹性本构关系表达式为[23]

(7)

(8)

(9)

其中,σij、Sij、σkk分别为应力张量、偏应力张量以及球应力张量;eij、εkk分别为偏应变张量及球应变张量;t为加载时间;E(t)为松弛模量,其Prony级数表达式为

(10)

为了后续计算,这里介绍推进剂蠕变柔量的Prony级数表达式:

(11)

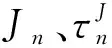
VEM处理线粘弹性材料的步骤与处理线弹性方法类似,读者可参考文献[13]。唯一和处理线弹性问题不同的是,VEM需要结合牛顿-拉夫逊方法才能全面展示出材料的粘弹特性,比如蠕变效应。此外,关于线粘弹性本构关系的离散与数值积分方法,可以参考文献[7,24]。

3 算例

3.1 单向拉伸粘弹性薄板应力松弛分析

考虑一长50 mm,宽10 mm的单位厚度长方形粘弹性薄板。约束薄板左侧的横向自由度并在右侧施加阶跃位移,由此模拟薄板在松弛阶段的粘弹性响应。

图2给出了薄板的网格以及边界情况。薄板材料松弛模量以及蠕变柔量的Prony级数参数见表1,泊松比取0.48。

图2 粘弹性薄板多边形网格及其边界Fig.2 Polygonal mesh and its boundaries of viscoelastic sheet

表1 推进剂松弛模量以及蠕变柔量Prony级数参数Table 1 Prony series parameters of propellant relaxation modulus and creep compliance

上述问题可以简化为一维模型进行处理。对于单轴问题,粘弹性的应力-应变关系可以描述为

(12)

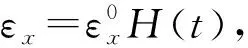
(13)

如图3所示,可以看到不同阶跃位移水平(3.75、7.5、15 mm)下,薄板轴向应力的数值解与解析解是一致的。上述仿真结果表明,VEM可以准确地模拟粘弹性结构的应力松弛效应。

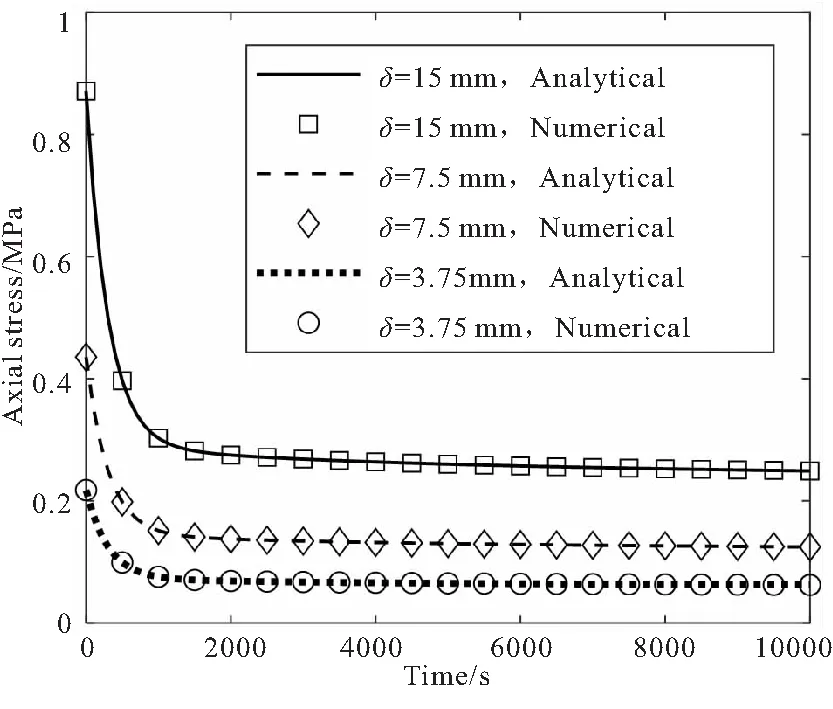
图3 不同阶跃位移下薄板的轴向应力响应Fig.3 Axial stress response of thin plates at different step displacements

3.2 双向拉伸粘弹性薄板蠕变分析

进一步地,为检验VEM模拟推进剂蠕变特性的能力,设计了以下双轴拉伸蠕变变形试验,如图4。该薄板长100 mm,宽50 mm,厚度为1 mm。在进行蠕变试验时,约束薄板的左侧横向位移以及下侧的竖向位移,并在右侧及上侧表面施加大小不同的均布法向载荷。薄板的材料参数与3.1节一致。

图4 粘弹性薄板多边形网格及其边界Fig.4 Polygonal mesh of viscoelastic sheet and its boundary

假设施加的均布载荷函数满足

(14)

结合边界条件和本构关系,不难计算出平面应力状态下薄板两个方向的应变响应为

(15)

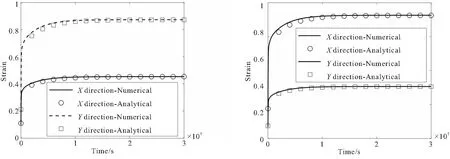
图5 应变随时间变化曲线Fig.5 Variation of strain with time

3.3 圆管形药柱点火增压分析

图6给出了一个圆管药柱的物理模型,药柱的内径a=200 mm,外径b=400 mm。药柱外侧受到固定约束,内表面受内压p(t)=p0(1-e-kt)的作用。其中p0为1.0 MPa,压力因子k取25,作用时间为0.3 s。药柱的材料参数与上文一致。

图6 圆管药柱物理模型Fig.6 Physical model of tube grain

针对上述粘弹性平面应变问题,药柱结构相应的应力-应变解析解表达式为

(16)

且有

式中σr和σθ分别为径向与环向应力;εr和εθ分别为径向与环向应变;r为径向坐标;t为加压时间;J∞为平衡蠕变柔量;fJ(t)为蠕变函数。

分别采用商业有限元软件ABAQUS、VEM以及解析的手段对圆管药柱受压问题进行求解。在ABAQUS中,采用1975个四节点四边形单元,节点总数为2080;VEM中多边形的总数为1000,节点总数为1994。两种数值仿真方法中总的自由度数接近。

图7给出了药柱内表面径向以及环向应力随时间变化的曲线,可以看到VEM方法计算出的结果与解析法以及ABAQUS方法得到的结果分布一致。另一方面,图8给出了加载至0.3 s时刻,应力、应变相对误差沿径向的路径分布,不难看出,两种仿真方法的计算结果与解析解相近。

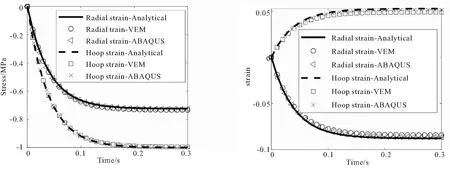
(a)Stress-time curves (b)Strain-time curves图7 圆管内表面的应力、应变随时间变化曲线Fig.7 Variation of stress and strain on the inner surface of cylinder with time

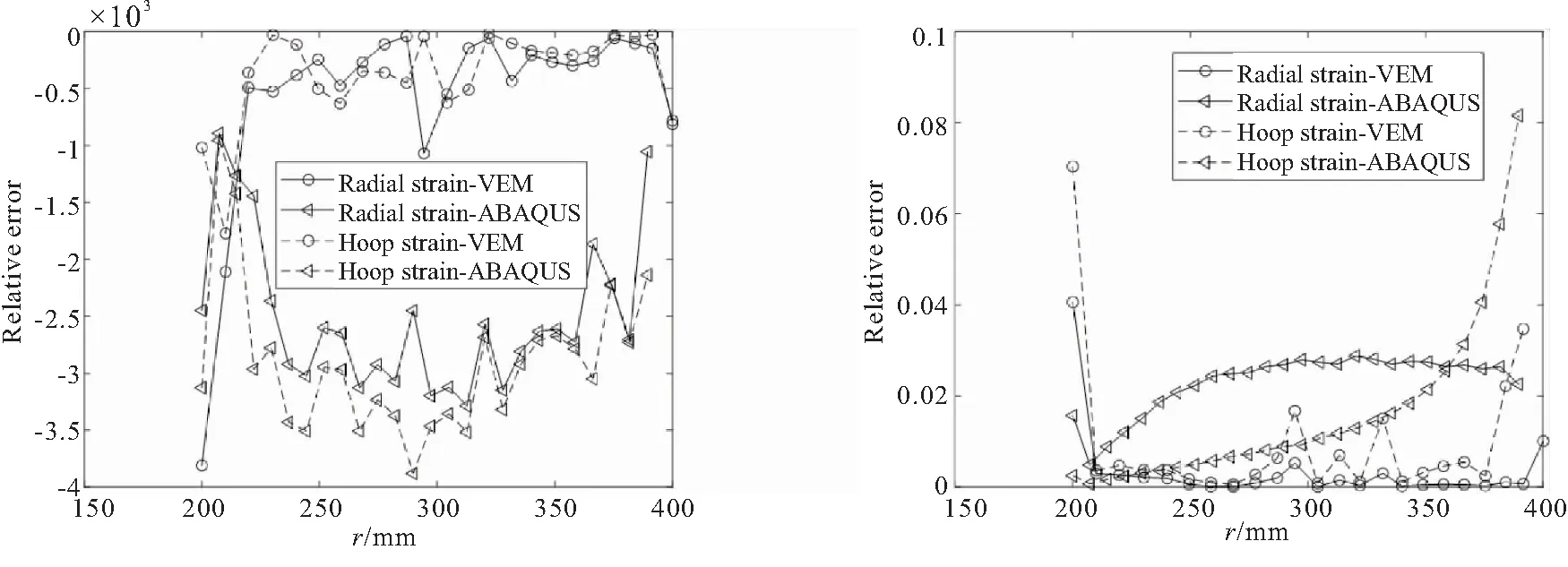
(a)Relative error of stress curves (b)Relative error of strain curves图8 加载至0.3 s时刻应力、应变相对误差沿径向变化曲线Fig.8 Relative error of stress and strain change along the radial direction at 0.3 s

图9和图10分别给出了加载结束时,圆管径向以及环向的应变云图,对比云图分布情况并结合上述结果,VEM手段在计算药柱结构受压时具有良好的分析精度。

(a)VEM (b)ABAQUS (a)VEM (b)ABAQUS图9 圆管径向应变云图 图10 圆管环向应变云图Fig.9 Radial strain contours of cylinder Fig.10 Hoop strain contours of cylinder

4 结论

本文为固体推进剂药柱的结构完整性分析提出了一种全新的技术手段。以二维问题为例,介绍了VEM实现的基本流程。针对线粘弹性的推进剂材料,开展了相关算例的仿真验证。

计算结果表明,VEM可准确模拟出粘弹性材料的松弛和蠕变响应。在点火增压条件下,VEM计算出的应力-应变响应与ABAQUS以及解析解吻合一致。从二维分析结果来看,VEM可以准确预示粘弹性结构在各种载荷下的应力-应变响应。结合VEM对网格形式的低依赖性,利用VEM开展复杂药柱结构完整性分析工作将会大幅提高网格前处理的效率。此外,VEM有望进一步应用于药柱的三维结构完整性分析以及推进剂裂纹扩展等领域。