改性双基推进剂非线性本构模型及其数值实现①

张 旭,刘向阳*,王士欣,闫晴霄,张广龙,张 源

(1.北京理工大学 宇航学院,北京 100081;2.中国船舶重工集团公司第七一三研究所,郑州 450015)

0 引言

复合改性双基推进剂(CMDB)是一种经典的固体推进剂,在导弹等武器系统中有广泛的使用。在硝化纤维素、硝化甘油中加入了固体氧化剂等组分后,其性能有了明显提升,但同时其内部组分间的多相界面使其力学性能变得更为复杂[1-3]。刘远祥等[4]进行了不同拉伸速率下CMDB推进剂的单轴拉伸试验,结果表明,CMDB推进剂的力学行为明显受到应变率的影响,随着应变率的增加,推进剂的应力-应变曲线逐渐出现“强化现象”。孙朝翔[5]在进行不同应变率下的CMDB压缩性能试验后发现,CMDB的压缩初始模量和屈服应力随着应变率的升高而升高。王鸿丽等[6]在分别进行CMDB拉伸和压缩试验后提出,CMDB具有明显的应力和应变拉压不对称性,其认为拉压不对称性是由材料初始缺陷的扩展等因素造成的。综上可知,CMDB推进剂的力学行为存在率相关性和拉压不对称性。在此基础上,发展出针对CMDB推进剂力学行为的本构模型和数值实现方式具有重要的意义。

针对CMDB推进剂的本构模型及其数值实现方式,国内外研究者展开了很多研究。孟红磊等[7-8]建立了CMDB推进剂的非线性粘弹性本构模型,利用UMAT将本构模型二次开发后,其分析了压力、星孔参数及包覆层材料对装药结构完整性的影响。沙宝林等[9]建立了CMDB推进剂统一本构,其中损伤水平由恢复应变能密度的方法预测,在UMAT二次开发后,对燃烧室力学行为进行了预测。以上本构模型具有参考价值。在加入固体填料后,CMDB推进剂与其他固体推进剂的力学性能较为类似。因此,在建立适用于CMDB推进剂的本构模型时,也可以参考其他类型固体推进剂等粘弹性材料的相关研究。SWANSON等[10]通过引入应变软化函数构建了高伸长率下的唯象型非线性本构模型,该软化函数类似于宏观损伤演化函数。许进升[11]基于端羟基聚丁二烯(HTPB)推进剂单轴试验和松弛试验,发展出基于Prony级数的损伤粘弹性本构模型并应用于发动机结构完整性分析。WANG等[12]使用了一种简单但形象的损伤变量形式来构建HTPB推进剂非线性本构模型,其损伤定义为衰减应力与线性粘弹性应力的比值。以上非线性本构模型均通过引入损伤变量(或软化函数)构建,需要在此基础上建立适用于CMDB材料的率相关性和拉压不对称性的损伤形式。损伤变量作为构建非线性粘弹性本构模型的关键参数,其演化规律对推进剂力学行为的描述意义重大。但目前还缺乏对CMDB推进剂损伤变量与应变率和拉压条件相关性的研究。

本文建立了改性双基推进剂含损伤的非线性粘弹性本构模型并推导了其增量形式。在通过单轴和松弛试验拟合得到本构模型的关键参数后,基于拉压不对称性发展出了本构模型的数值实现方式。最后,利用该本构模型和数值实现方式对点火冲击载荷下的燃气发生器药柱力学响应做出分析。

1 本构模型

根据文献[12],固体推进剂的非线性本构模型可定义为

(1)

式中σ(t)为应力;ε(t)为应变;E(t)为松弛模型;ρ为积分变量。

损伤变量D定义为衰减应力所占线粘弹性应力σL的比值,其取值范围为[0,1],当D=0时表示材料无损伤,当D=1时表示材料破坏。

当使用由广义Maxwell模型得到的Prony级数形式松弛模量作为积分型本构模型中的松弛模量时,得到的非线性本构模型为

(2)

如果应变率为恒定值,其可表示为

(3)

代入式(2)得到积分后恒应变率下的本构模型:

(4)

为后续分析便捷,定义线性粘弹性应力为

(5)

以上得到一维条件下全量型非线性粘弹性本构模型。在材料的变形过程中,很难保持恒定的应变率。因此,需要推导本构模型的增量形式,并对应变率进行更新。在t时刻,材料的损伤变量为D(t);在t+Δt时刻,材料的损伤变量为D(t+Δt)。则在时间增量Δt内,材料的应力增量略去高阶项后表示为

Δσ(t)≈[1-D(t+Δt)]σL(t+Δt)-[1-D(t)]σL(t)

=[1-D(t)]ΔσL(t)-[ΔD(t)]σL(t)

(6)

当时间增量Δt足够小时,在Δt内,材料的应变率可表示为

(7)

线性粘弹性应力增量为

ΔσL(t)=σL(t+Δt)-σL(t)

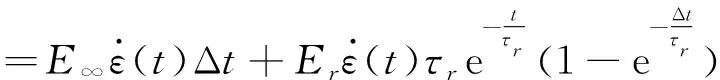
(8)

因此,式(6)可表示为

(9)

以上得到的增量形式本构模型中,应变率可随着时间不断更新,故该增量型本构模型能预测复杂应变率下材料的大变形粘弹性力学行为。

2 试验与参数拟合

2.1 单轴试验及松弛试验

针对CMDB推进剂存在的拉压不对称性问题,为准确分析拉伸和压缩条件下材料的力学响应,本研究中分别进行拉伸和压缩条件下的单轴和松弛试验来获得所建立非线性粘弹性本构模型的参数。单轴拉伸和拉伸松弛试验使用哑铃板材试样,单轴压缩和压缩松弛使用圆柱棒材试样,哑铃试样和圆柱试样尺寸如图1所示,单位为mm。单轴拉伸和压缩试验在万能试验机中进行,试验温度为20 ℃。拉伸速率分别选取2、10、50、100 mm/min,对应的应变率分别为6.67×10-4、3.33×10-3、1.67×10-2、3.33×10-2s-1;压缩速率分别选取2.5、10、50、100 mm/min,对应的应变率分别为1.39×10-3、5.55×10-3、2.78×10-2、5.55×10-2s-1。每种条件进行5组试验,选取5组试验真实应力和应变的平均值绘制应力-应变曲线,拉伸和压缩条件下应力-应变曲线如图2所示。

(a)Tensile specimen

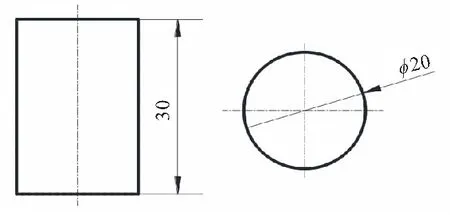
(b)Compressive specimen图1 试件尺寸图Fig.1 Structures of test specimens

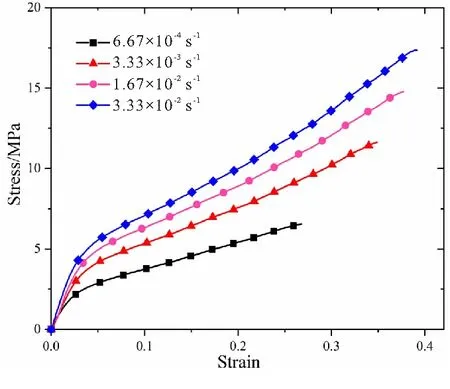
(a)Tensile curves

(b)Compressive curves图2 单轴试验应力-应变曲线Fig.2 Stress-strain curves of uniaxial tests

图2中,当应变较小时,材料处于线性粘弹性范围;当应变达到某一数值时,应力-应变曲线出现一个模量突减的现象,该模量突减的点被称为“损伤点”,该点对应的应变值被称为“损伤阈值”[13]。且拉伸和压缩应力-应变曲线中,随着应变率的增加,应力有明显的增加,即CMDB推进剂存在明显率效应。

拉伸和压缩松弛试验中,试验温度为20 ℃,初始恒定应变为5%,松弛时间为1200 s,进行5组试验。一般认为,采用6阶Prony级数能准确描述CMDB的松弛性能,将松弛模量和松弛时间按照式(2)拟合为6阶Prony级数形式,拟合结果如表1所示。

表1 松弛模量参数Table 1 Relaxed modulus parameters

2.2 损伤变量拟合

利用式(4)计算得到10 mm/min加载速率下拉伸及压缩条件下损伤变量演化曲线如所图3所示。由图3可知,在未产生损伤时,线性粘弹性应力-应变曲线与真实应力-应变曲线重合度较好,此时损伤值为0。在产生损伤后,真实应力明显小于线性粘弹性应力。损伤变量随着应变的增加而增加,直至达到一个数值并保持稳定。在这一模量稳定的区间内,损伤变量也保持稳定。其后,当应变达到最大伸长率后,损伤变量迅速增加至1。

(a)Tensile damage variable (b)Compressive damage variable图3 10 mm/min加载速率下损伤变量演化曲线Fig.3 Damage variables evolution curves at 10 mm/min loading rate

损伤变量随应变近似满足指数分布。拉伸条件下CMDB推进剂的损伤变量在初始阶段随应变的增加速率小于压缩条件,且拉伸损伤变量的最终稳定值也小于压缩损伤变量的稳定值。

由应力应变数据计算得到的不同应变率下的损伤变量如图4散点所示。由图4可知,随着应变率的增加,损伤阈值有所增加,但增加的幅值逐渐减小,呈指数型演化。同时,在不同应变率下,最大伸长率处拉伸损伤变量数值(图4最终值)变化的范围宽于压缩情况。整体而言,CMDB推进剂的损伤变量与应变率呈“负相关”。且拉伸条件下相关性强于压缩条件。

(a)Tensile damage variable (b)Compressive damage variable图4 双指数型损伤变量与试验结果对比Fig.4 Comparison of double exponential damage variables with tests

由式(8)相关理论可知,当应变率增加时,线性粘弹性应力呈比例增加,损伤变量计算的分母更大。此外,当应变率较高时,推进剂的模量更高[5],更不容易发生损伤。以上两点原因共同导致损伤变量与应变率呈“负相关”特性。

在应变较大时,随着应变的增加,损伤变量数值有所减小,这是由于推进剂材料在非线性段存在一定的“强化现象”[4],即模量随应变增加而增加的现象。当模量增加时,损伤变量数值会减小。

文献[14]中,将与应变率呈对数关系、与围压强度呈指数关系的损伤变量表征为对数与指数结合的形式。本文中,将与变形状态与应变率均呈指数关系的损伤变量表征为双指数形式。

当ε>εth时,损伤变量定义为

(10)

式中εth为损伤阈值;A1、A2、A3、A4和A5为损伤变量中的参数。

当ε≤εth时,损伤变量D=0。其中,包含应变率的指数项用于表征损伤变量与应变率的“负相关”性,即B2应为负值。

损伤阈值表达式为

(11)

式中Ath、Bth和Cth为损伤阈值参数。

由双指数损伤变量模型拟合得到的损伤变量及损伤阈值参数结果如表2所示。

表2 损伤变量及损伤阈值参数Table 2 Damage variable and damage threshold parameters

双指数形式的损伤变量计算结果如图4实线所示。由图4对比可知,双指数形式的损伤变量与实验结果具有很好的一致性(拉伸损伤变量拟合相关系数为0.993 8,压缩损伤变量拟合相关系数为0.993 0)。

3 数值实现

利用Abaqus中的User-Material Subroutine (UMAT)用户材料子程序建立本构模型的数值实现方法,UMAT子程序中进行应力状态判定和应力更新的流程如图5所示。

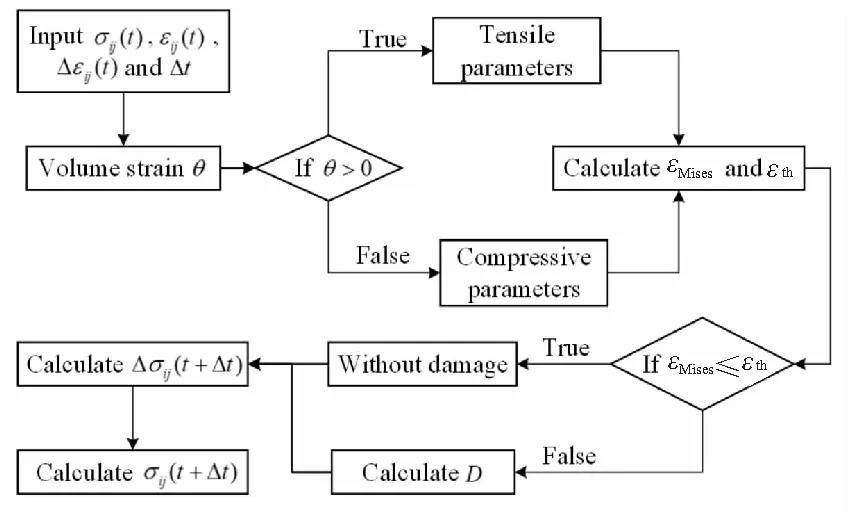
图5 应力更新流程图Fig.5 Flow chart of stress update

应力更新过程中,关键的部分有:

(1)变形状态判别

因为CMDB材料存在拉压不对称性,因此,必须对单元所处的拉伸和压缩状态进行区分。对单元受力状态的判断采用体积应变来判断,体积应变指物体单位体积的改变量。

三维应变单元的体积应变为[15]

(12)

式中θ为体积应变,其数值与第一应变不变量I1相同;V为变形前体积;V′为变形后体积;εx、εy和εz分别为沿x、y和z方向的应变。

(2)应变率计算

在本文的研究中,选用Mises等效应变作为损伤状态的判断量,选用Mises等效应变率用于损伤阈值、损伤变量和松弛修正系数的计算。

等效应变基于UVARM子程序获得。使用等效应变率可以避免因为选取不同方向的应变而导致节点出现变形状态的判断差别。等效应变率的计算表达式为

(13)

4 本构模型应用

4.1 有限元模型

在建立非线性本构模型及其数值实现方式后,本节对某型燃气发生器单根药柱结构在点火冲击载荷下的力学响应进行分析。燃气发生器单根药柱结构如图6所示,包括药柱、包覆层、挡药板和弹性垫圈等部件。

图6 燃气发生器单根药柱结构Fig.6 Structure of single gas-squeezer grain

该型燃气发生器单根药柱长度约为0.5 m。点火冲击载荷基于燃气发生器常温测试试验得到,在20 ms内,药柱内外表面压强线性增加至10 MPa。分析中使用到的材料参数如表3所示。

目前，各级图书馆推出了许多特色鲜明的阅读推广活动，经过多年的发展，已经成为文化建设的重要组成部分，但多数图书馆门户网站并没有阅读推广平台[3]。要想吸引具有思想和活力的读者走进图书馆，达到阅读推广的预期效果，只有树立阅读推广的品牌意识，并借助阅读推广平台进行有效的宣传，才能达到阅读推广的预期效果。建立有特色的阅读推广平台，并进一步扩大图书馆的品牌效应，即是图书馆品牌文化营销。通过阅读积分制，可以将阅读推广活动常态化并且形成一种长效机制，从而将图书馆的品牌深入读者的内心。同时，将导读内容与图书馆的阅读推广活动及成果等融合起来，打造特色文化传播平台。

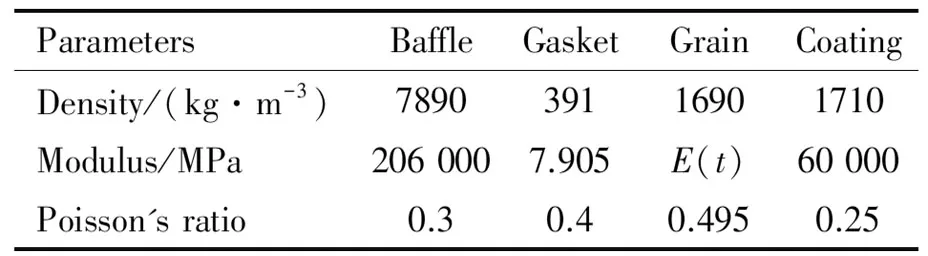
表3 燃气发生器药柱组件材料参数Table 3 Material parameters of gas-squeezer assemblies

药柱结构划分C3D8H网格,共501 520个单元;其他结构划分C3D8网格,共60 971个单元。挡药板外表面施加固定约束边界条件,点火冲击载荷作用在所有部件的外表面,不同部件接触面施加绑定约束。

4.2 结果分析

点火冲击载荷作用后,药柱结构体积应变云图如图7所示。由图7可知,在点火冲击载荷作用下,整个药柱的体积应变均为负值,即药柱处于压缩状态。因此,在对结构进行力学响应分析时,UMAT自动选择压缩本构参数。同时,由体积应变云图可得,药柱两端面处变形最大。

图7 药柱体积应变Fig.7 Volume strain of grain

点火冲击载荷作用后,药柱端面等效应力-应变云图如图8所示。可见,由于与挡药板的接触压力,挡药板端的应力分布较为复杂。挡药板端最大等效应力为3.704 MPa,最大等效应变为1.035%。

(c)Equivalent stress at the end of gasket (d)Equivalent strain at the end of gasket图8 药柱等效应力应变Fig.8 Equivalent stress and strain of grain

相较于挡药板端,垫圈端药柱的等效应力较为规整,药柱的应力呈圆环状分布。中间部位应力-应变数值较大,表面和内孔处数值较小,这是由于内外表面共同向中间部位挤压造成。垫圈端最大等效应力为8.321 MPa,最大等效应变为3.139%。

药柱的最大力学响应在垫圈端,故对垫圈端的损伤做出分析,含包覆层药柱垫圈端损伤变量分布如图9所示。由图9分析可知,药柱结构仅有垫圈端药柱中心区域发生了损伤,最大损伤变量数值为0.157,即该部分区域进入非线性粘弹性范围。除靠近端面部位外,其余大部分部位仍处于线性粘性粘弹性范围,即未发生损伤。

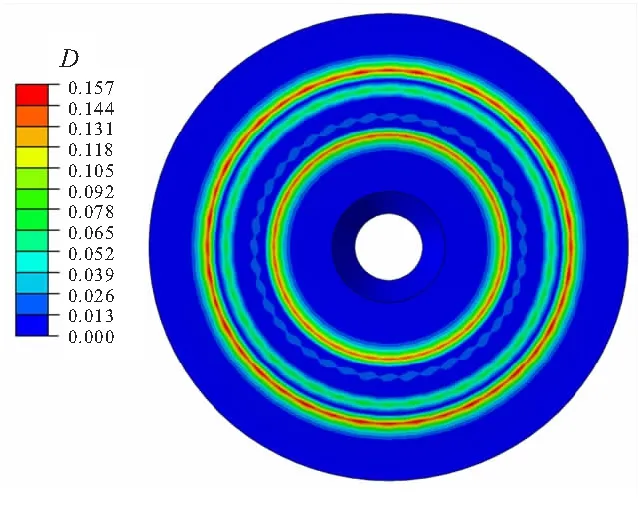
图9 垫圈端损伤变量Fig.9 Damage variable at the end of gasket

为验证考虑拉压不对称性的必要性,采用拉伸本构参数对点火冲击载荷作用下药柱的力学响应进行分析并与前序结果对比。当不考虑拉压不对称性,仅使用拉伸本构参数用于结构力学响应分析时,计算得到药柱的等效应力-应变分布情况与考虑拉压不对性时相同,但数值有所差别。

拉伸参数分析得到的垫圈端损伤云图如图10所示。由图10可知,使用拉伸参数计算得到的损伤变量最大值为0.023,远小于考虑拉压不对称性时的损伤变量最大值(0.157,见图9)。

图10 基于拉伸参数的垫圈端损伤变量Fig.10 Damage variable at the end of gasket based on tensile parameters

以上现象由两个因素导致:

(1)在较高应变率下,拉伸损伤阈值大于相同应变率下的压缩损伤阈值;

(2)在发生损伤后,拉伸损伤变量的增加幅度慢于压缩损伤变量(见图4)。

综上所述,在对复杂载荷作用下的结构进行力学响应分析时,考虑CMDB推进剂的拉压不对称性,判断结构的变形状态并选择准确的参数具有必要性。

5 结论

本文构建了改性双基(CMDB)推进剂非线性本构模型并发展了其数值实现方式,得到的主要结论如下:

(1)通过单轴试验和松弛试验构建了含损伤变量的非线性本构模型。试验结果表明,在应变小于损伤阈值时,损伤变量接近于0;当应变大于损伤阈值时,损伤变量随应变呈指数型增加。

(2)CMDB推进剂的损伤变量与应变率呈“负相关”,拉伸条件下相关性强于压缩条件。使用包含应变和应变率的双指数可以准确描述与变形状态与应变率相关的损伤变量。

(3)引入将体积应变作为拉压状态的判定变量,基于UMAT子程序完成了考虑拉压不对称的CMDB推进剂本构模型数值实现。

(4)将数值实现方法应用于燃气发生器药柱在点火冲击下的力学响应分析。与使用单一拉伸参数时进行力学响应分析的结果相比,考虑拉压不对称性时结构的等效应变更小,但损伤变量更大。考虑拉压不对称性并选用准确参数具有重要意义。