基本初等函数问题化教学之课例探究

蔡一帛

［摘  要］ 文章拟运用课堂教学行为大数据的分析方法，辅以问题化教学原理课模型，展开基本初等函数问题化教学课例分析. 通过问题支架搭建，帮助学生探索研究路径，提升师生深度对话，促进学生对知识的理解，实现课堂深层学习.

［关键词］ 基本初等函数；问题化教学；课堂深层学习

《普通高中数学课程标准（2017年版2020年修订）》指出：“高中数学教学以发展学生学科核心素养为导向，创设合适的教学情境，提出合适的数学问题，启发学生思考，引导学生把握教学内容的本质. ”［1］基于课标理念，在课时设计过程中，把握本课时重难点以及核心素养培养，积极探索引导学生思维衔接点的问题系统是教育工作者关心的重要问题. 在当前有关数学问题化教学的研究中，研究者普遍认为，发现和提出问题，相较于解决问题更能集中体现学生的数学思维水平，是培养学生创新思维和创造力的主推力；但是，关于函数教学的研究，目前主要集中在函数图象与性质及其应用等方面，对高中课堂教学问题链的有效性设计研究相对不足. 因此，作者就“如何实现函数问题化教学，培养学生的高阶思维”这一问题，以“函数f（x）=Asin（ωx+φ）的图象”为案例展开研究，基于“课例研究起点、课例研究过程、课例研究改进”的思路，探究高中数学问题化教学的有效路径.

课例研究起点：研读课标，以问题教学推动课堂转变

基本初等函数的学习旨在用函数观点和方法分析具体问题的函数模型，发现事物的运动变化规律. 这对数学抽象素养的要求较高. 《普通高中数学课程标准（2017年版2020年修订）解读》指出：“概念形成过程的实质是抽象出某一类对象或者事物的共同本质特征的过程.”［2］章建跃博士在《“单元一课时教学设计”体例与要求》中建议：“从‘问题串中归结出一节课的流程.”［3］故本文拟采用问题化教学模式，借用首都师范大学王陆教授团队对课堂教学行为大数据采集分析方法［4］，围绕函数课例核心问题的研究与解决，激发学生对核心问题进行深度探究和思考，力求通过教师问题化的“教”，培养学生学会问题化“学”的思维技能.

课例研究过程：以“函数f（x）= Asin（ωx+φ）的图象”为例

依据课例研究起点，现以“函数f（x）=Asin（ωx+φ）”为例，探寻问题链教学模式在课堂实际中的运用.

1. 教学设计分析：运用追问式教学，预设教学目标、重难点与策略

（1）“函数f（x）=Asin（ωx+φ）的图象”的教学目标与重难点.

本节课的教学目标包含两方面内容：①从现象看本质：通过质点匀速圆周运动变化过程的观察，抽象出数学本质问题，即函数f（x）=Asin（ωx+φ）中各参数对图象变化的影响，并进一步理解由质点变化到曲线变化的迁移过程；②通过对正弦曲线的平移、伸缩变换过程的实操，明确函数f（x）=Asin（ωx+φ）中各参数的内在联系. 引导学生达成教学目标，提升学生的直观想象、数学抽象和数学表达素养.

基于上述教学目标，笔者认为本节课的教学重难点如下：①筒车运动的背景条件综合性强，对学生数学建模能力的要求较高；②研究参数对函数f（x）=Asin（ωx+φ）图象的影响，其分析顺序以及关联研究对学生逻辑思维能力的要求较高；③在正弦曲线经变换得到函数f（x）=Asin（ωx+φ）的图象的过程中，对平移、伸缩等变换的准确表述.

（2）“函数f（x）=Asin（ωx+φ）的图象”的教学策略.

针对上述教学目标与重难点，提出教学策略如下. ①采用问题化教学：围绕教学目标展开问题系统设计；层进式突破问题猜想：探索参数φ对函数f（x）=sin（x+φ）图象的影响，然后通过类比探究，逐步解决參数A，ω对函数f（x）=Asin（ωx+φ）图象的影响. ②采用信息技术手段实现对筒车现实情境的动态几何呈现，逐步代数化，引导学生分析各参变量之间的内在联系，以直观感受函数f（x）=Asin（ωx+φ）中各参数的作用，突破重难点.

2. 教学过程设计：厘清问题链条，明晰主线环节

通过上述分析，可得教学设计重点为表1所示的5个环节（表1呈现了各个环节的教师活动、学生活动、活动说明及设计意图）.

课例设计有效问题链，通过引导、观察、讨论等多个探究路径，围绕教学目标展开探究，努力营造一个师生共同参与的交互式探究过程，遵循问题化教学原理的基本流程：提出问题→形成猜想→枚举、论证、归纳结论→运用结论. 课例设计以下问题进行分析.

（1）问题引入，激发思维.

数学核心素养关注的是学生的数学思维以及数学发展能力. 在数学学习时，提出有效问题是学生探求知识与发展科学思维的原动力. 本节课主要研究参数对函数图象的影响，如何引导学生发现参数变化对图象的影响是关键，以问题形式引导学生参与各环节的探究是重点.

以如下问题为例：半径为A m的筒车逆时针做角速度为ω rad/min的匀速圆周运动. 如果筒车上的点P从P处开始计算时间：若P置于x轴的正半轴上，请在平面直角坐标系中确定时刻x min时的点P的纵坐标y. 若P置于图1的位置时呢？

通过上述问题情境的设立，引发学生思考与探讨参数φ，ω，A与变量x，y之间的关系，利用问题驱动激发学生的数学思维，进而展开探究实践活动.

（2）图象探究，提升认知.

教学目标之二是探索各参数对函数图象的影响，此时，问题链系统设计是师生互动的行动方向，目标是提升学生的数学思维能力与数学素养，有效提高课堂学习深度. 本节课为研究参数φ对函数f（x）=sin（x+φ）图象的影响设计如下问题.

问题1 观察函数y=sinx与函数y=sinx+的图象的关系，猜测函数解析式与图象的关联性（借助信息技术进行实验探究：引导学生观察图2）.

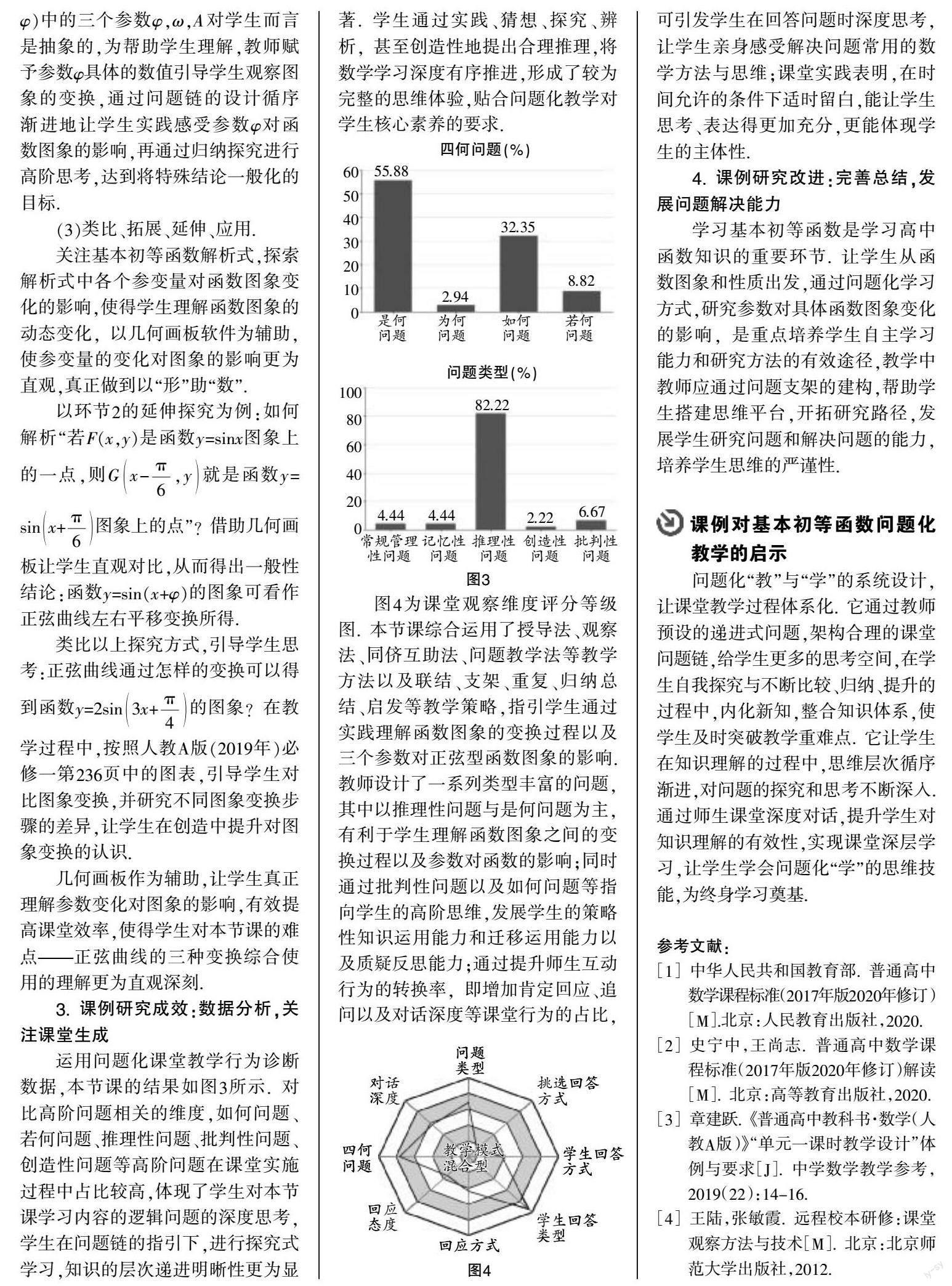
圖4为课堂观察维度评分等级图. 本节课综合运用了授导法、观察法、同侪互助法、问题教学法等教学方法以及联结、支架、重复、归纳总结、启发等教学策略，指引学生通过实践理解函数图象的变换过程以及三个参数对正弦型函数图象的影响. 教师设计了一系列类型丰富的问题，其中以推理性问题与是何问题为主，有利于学生理解函数图象之间的变换过程以及参数对函数的影响；同时通过批判性问题以及如何问题等指向学生的高阶思维，发展学生的策略性知识运用能力和迁移运用能力以及质疑反思能力；通过提升师生互动行为的转换率，即增加肯定回应、追问以及对话深度等课堂行为的占比，可引发学生在回答问题时深度思考，让学生亲身感受解决问题常用的数学方法与思维；课堂实践表明，在时间允许的条件下适时留白，能让学生思考、表达得更加充分，更能体现学生的主体性.

4. 课例研究改进：完善总结，发展问题解决能力

学习基本初等函数是学习高中函数知识的重要环节. 让学生从函数图象和性质出发，通过问题化学习方式，研究参数对具体函数图象变化的影响，是重点培养学生自主学习能力和研究方法的有效途径，教学中教师应通过问题支架的建构，帮助学生搭建思维平台，开拓研究路径，发展学生研究问题和解决问题的能力，培养学生思维的严谨性.

课例对基本初等函数问题化教学的启示

问题化“教”与“学”的系统设计，让课堂教学过程体系化. 它通过教师预设的递进式问题，架构合理的课堂问题链，给学生更多的思考空间，在学生自我探究与不断比较、归纳、提升的过程中，内化新知，整合知识体系，使学生及时突破教学重难点. 它让学生在知识理解的过程中，思维层次循序渐进，对问题的探究和思考不断深入. 通过师生课堂深度对话，提升学生对知识理解的有效性，实现课堂深层学习，让学生学会问题化“学”的思维技能，为终身学习奠基.

参考文献：

［1］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］ 史宁中，王尚志. 普通高中数学课程标准（2017年版2020年修订）解读［M］. 北京：高等教育出版社，2020.

［3］ 章建跃. 《普通高中教科书·数学（人教A版）》“单元一课时教学设计”体例与要求［J］. 中学数学教学参考，2019（22）：14-16.

［4］ 王陆，张敏霞. 远程校本研修：课堂观察方法与技术［M］. 北京：北京师范大学出版社，2012.