一道中考二次函数综合题的解法探究*

合肥师范学院数学与统计学院(230601) 程丽雲 张新全

1 真题呈现

(2022 年福建省中考数学第25 题) 在平面直角坐标系xOy中,已知抛物线y=ax2+bx经过A(4,0),B(1,4)两点.P是抛物线上一点,且在直线AB的上方.

(1)求抛物线的解析式;

(2)若ΔOAB面积是ΔPAB面积的2 倍,求点P的坐标;

(3) 如图1,OP交AB于点C,PD//BO交AB于点D.记ΔCDP, ΔCPB, ΔCBO的面积分别为S1,S2,S3. 判断是否存在最大值. 若存在,求出最大值;若不存在,请说明理由.

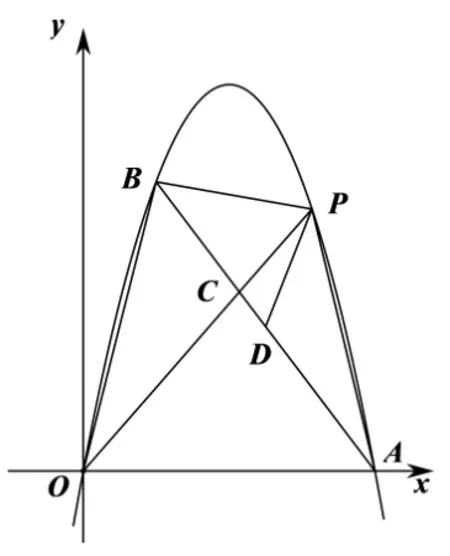
图1

图2

图3

图4

2 试题解读

本题是2022 年福建中考数学压轴题,以二次函数与平面几何知识为背景,重点考查了与二次函数有关的面积问题.该题涉及的数学核心概念主要有: 一次函数、二次函数的图象与性质、三角形的面积、锐角三角函数以及相似三角形的判定与性质等;本题蕴含的数学思想方法主要有: 数形结合思想、函数与方程思想、数学建模思想、转化思想和分类讨论思想等;本题考查的数学核心素养主要有: 运算能力、推理能力、空间观念、几何观念和创新意识等.

三个小题由浅入深,层层推进. 第(1)小题涉及求二次函数解析式,主要考查待定系数法、方程思想等;第(2)小题中ΔOAB与ΔPAB具有公共边,ΔOAB的面积是ΔPAB面积的2 倍, 则以AB为底的两三角形的高也具有倍半关系.本题可以考虑的思路较多,最直接的方法是利用公式法分别将两个三角形的面积用坐标表示出来,分别将两个三角形的面积用坐标表示出来,建立等量关系即可求解出点P的坐标,也可以根据面积比转化为高的比,进而可以转化为线段PC与OC的长度之比,再转化为坐标之比,进而求出点P的坐标;第(3)小题在第(2)小题的基础上求面积比和的最大值,继续深入研究三角形面积问题.这是近两年以来考查比较多的问题,通常考查两个共边三角形面积之比的最值,利用A 字型或者X 字型的相似转化为求线段的最值.而解决这一问的关键是充分利用平行得到相似三角形,最终通过将三角形的面积比转化为线段比,从而直达本真,化繁难为简捷,求解出比值的最值. 而学生需要实破的第一点是利用有公共边的三角形同底不同高或同高不同底的性质,将面积比转化为线段比或者相似比,第二点是斜线段的比值转化成竖直或者水平线段之比,充分体现了转化的思想,转化过程需要学生巧妙添加辅助线,灵活运用数学知识,这对学生的思维水平有较高要求,同时学生需要进行细致的观察、合理的联想、缜密的推理,具有较大的难度和挑战性.

3 解法探究

3.1 第(1)小题解法

3.2 第(2)小题解法

3.3 第(3)小题解法

思路一: 构造“A 型”相似求解

解法1 因为PD//BO, 所以∠DPC= ∠BOC,

解法2如图5, 过点D向y轴作垂线DS, 分别过点B、点C向x轴作垂线BS和CT. 因为直线OB的解析式为:y= 4x,则可设直线PD的解析式为y= 4x+b,设点

图5

解法3如图6, 过点P作AB的平行线l. 设点P的

图6

因为抛物线与平行线l只有一个交点, 所以Δ = 0,

点评通过作平行线段构造“A 型”相似,证明三角形相似,由相似三角形的性质将问题转化为平行线分线段成比例是解决此类问题的通性通法.思路二: 构造“X 型”相似求解

解法4如图7,过点C作CM⊥y轴,垂足为M,延长CM到点N,过点P作PN⊥CM于N. 因为PN//OM,所

图7

解法5 如图8,过点P作PR⊥x轴,交AB于点R,延长

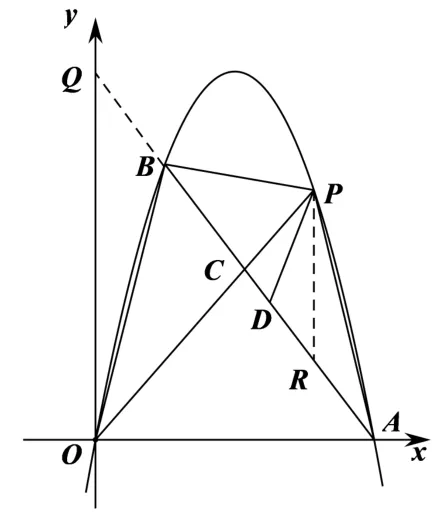
图8

所以当m=

解法6 如图9, 过点P和O分别作AB的垂线,垂足分别为M和N. 因为PM//ON, 所以∠PMC=∠ODC, ∠MPC= ∠NOC, 则ΔPMC∽ΔONC, 所以因为PM和ON是ΔABP和ΔABO的

图9

点评通过作垂线构造“X 型”相似,利用相似三角形的性质将问题就转化为求线段比值之和最大值,然后设未知量列方程,是求解此类问题的常见求解策略.

思路三: 利用位似比求坐标比

点评位似法是解决与线段有关的几何问题的常用方法.利用三角形位似比设出点C的坐标比,将点C代入直线AB中,可直接将直线AB的解析式转化为二次函数的形式,最后利用二次函数的性质即可求出最值.

思路四: 利用三角函数求解

解法8如图10, 过点P向x轴作垂线PT,过点D向PT作垂线DT,二者交于T.轴, 所以∠TDA= ∠DAO,且∠PDB是定值. 所以∠PDT是定值, 在RtΔPRD中, sin ∠PDT也 是 定 值,

图10

解法9同解法8, 在RtΔPRD中, cos ∠PDT是定

点评在RtΔPRD中借助“三角函数”由∠PDT的正余弦值推理得到线段PT或DT与线段PD间的长度关系,最后利用点坐标表示出线段的二次函数方程,求出的最大值.

4 解后反思

通过多视角的解题分析可以发现,2022 年福建中考数学对二次函数综合题的考查立意新颖,灵活多样,不仅考查了学生对函数基本知识的掌握情况,还考查了他们的数学思维能力与数学学科核心素养. 中考二次函数综合题具有极高的灵活性和多样性,没有一种固定的解决方法[2]. 因此,在日常教学中,教师可以依托解题活动训练学生数学思维,注重多视角分析综合题,对综合题进行一题多解的思考与探究,帮助学生形成运用数学思维方法寻找解题思路的习惯,培养从多个角度分析和解决问题的能力.