关于人教版选择性必修一中两种距离公式统一性的思考

广东省东莞市第八高级中学(523629) 何国锋

1 问题提出

人教版选择性必修第一册在“1.4.2 用空间向量研究距离、夹角问题”[1]中借助投影向量给出了空间内点P到直线l的距离公式:

√

(v为直线的方向向量,v0为直线的单位方向向量,A为直线上一点)以及点P到平面α的距离公式:

(n为平面的法向量,n0为平面的单位法向量,A为平面α内一点).

教材关于两个公式推导方式: 公式1○用到了的是向量在直线方向向量v上的投影向量以及勾股定理; 公式2○用到了的是向量在平面的法向量n上的投影向量,这么处理充分发挥了向量的工具作用,巧妙的利用了投影向量,学生也比较容易理解和接受. 但从公式的结构上来看公式1○显然比较复杂,不是十分美观,学生也不便于记忆. 笔者的思考是: (1)教材为什么采用在不同的向量上的投影向量来处理呢? (2)这两个公式能否统一,使得公式更加简洁美观呢?

2 问题解决

首先,要统一我们必须给出一个与直线垂直的向量,我们可以类比平面的法向量定义,来定义直线的法向量:

定义设直线l在平面α内,我们把所在直线垂直于l且平行于平面α(或在α内)的非零向量n称为直线l在平面α内法向量(如图一所示).

图1

如图2, 设点P与直线l(P在l外) 所确定的平面为α, 已知直线在平面内的法向量为n,A为直线l上一点, 则P到l的距离为在n上的投影向量的长度即

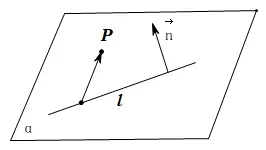
图2

由此,借助直线的法向量以及平面的法向量我们可以将两个公式1○2○统一为:

其中: (1)当是点到直线线距离时,设l与点确定的平面为α,n为l在平面α内法向量;A为直线上一点;

当是点到平面距离时,n为平面的法向量;A为平面内一点.

接下来,我们如果要用公式3○来求点到直线的距离,必须解决的问题如何求直线l在平面α内的法向量呢? ,在此提供如下两个方法:

方法1: 如图3,设l与点P确定的平面为α,其中α法向量为m,直线l的方向向量为v,所求直线的法向量为n,则利用n ⊥m,n ⊥v即可求出一个直线l在平面α内法向量.

图3

方法2: 如图4,设l与点P确定的平面为α,向量a,b为α内不共线的向量,所求直线的法向量为n,根据向量共面定理,存在实数x,y,使得n=xa+yb,最后利用n ⊥v(v为直线方向向量)即可求出一个直线l在平面α内法向量.

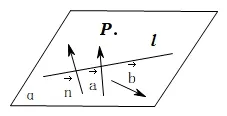
图4

图5

3 应用举例

例题1在四棱锥P -ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,求A到BE的距离.

通过以上分析与应用,我们将两种距离公式在结构上进行了统一,使得公式更加美观,学生也更加便于记忆和运用,同时推导过程使学生对距离的本质的理解以及向量在几何中的作用影响更为深刻. 不仅如此,如果将公式运用平面解析几何中点到直线距离公式的推导过程中,就可以避免教材推导过程[2]中的复杂计算, 可以节约时间也便与学生记忆,还可以进一步让学生体会到数学的和谐和统一美[3].

例题2(推导平面内点到直线的距离公式) 设直线l:Ax+By+C=0,点P(x0,y0),求P到直线l的距离.

解: 如图6, 易知l的方向向量V= (B,-A), 设其法向量为n= (x,y), 由n ⊥ v得,Bx -Ay= 0, 令x=A, 则y=B, 即n= (A,B). 设Q(x1,y1) 为直线上一点, 则Ax1+By1+C= 0,= (x0-x1,y0-y1), 从而,· n=A(x0-x1) +

图6