化归思维下数学微专题教学初探*

北京师范大学淮安学校(223001) 杨兴刚

进入高三,复习课成了课堂教学的主要课型,复习课的质量决定着学生数学思维的深度、方法的熟练度和数学素养的高度. 微专题教学是高三数学二轮复习课主要课型,开展微专题教学有利于学生在探究活动中不断深化知识理解、积累解题经验、强化模型识别、感悟数学思想和提升数学素养.G·波利亚曾经指出:“良好的组织使得所提供的知识容易用上,这甚至可能比知识的广泛更为重要.”二轮专题复习以思想方法为主线设计微专题,通过“变式教学”设计习题串,让学生跳出“题海战术”,真正体会习题“变”中的“不变”,形成解决问题的模型思想,化归试题的本质理解,提升自身的思维深度和数学素养.

1 化归思维及微专题教学内涵

化归思维的本质是转化和归结,是学生数学解题中常用的一种的思维方式. G·波利亚在《怎样解题》中指出:“我们在解题时总是得益于以前曾解过的那些题目,应用它们的结果或者方法,或是我们在解答它们当中所获得的经验[1]. ”数学中的“化归”方法,是指数学家们把待解决或未解决的问题,通过某种转化过程,归结到一类已解决或者比较容易解决的问题中去,最终求得原问题解答的一种手段和方法,即通过数学的内部联系利用矛盾转换,归结为规范问题或可求解问题的思想方法[2].

“微专题”通常是指围绕复习的重点和关键点设计的、利用具有紧密相关性的知识或方法形成的专项研究,或者结合学生的疑点和易错点整合的、能够在短时间内专门解决的问题集[3].

基于化归思维的微专题教学设计,有利于培养学生习题的模型感知能力,体会多题归一的思想统领性,强化解题经验积累,培养敢于突破的自信心和决战数学考场的决心. 化归思维视域下的微专题教学本质上是培养学生转化试题背景、挖掘思维共性、归类思想主线、规范解题过程、总结解题经验的过程.

2 化归思维视域下的微专题教学策略

2.1 以教材为基,深化知识理解

教材不仅是学生知识习得、技能建构的起点,也是高考模考试题命题的源头,是高三复习必须回归的起点. 在复习课中,“以教材为基”不是对教材索然无味的解读与重复,而是以教材为地基的思维深层次架构,教学要厘清问题的本质,体现数学的基本思想内涵和数学思维的建构过程,让教材成为引领学生深耕细作的沃土.

数列的本质是一类特殊的函数,数列的研究对象是数学中或现实中具有递推规律的事物,在日常生活中也有着广泛的应用. 等差数列和等比数列是数列递推关系中最基本的两种关系,通过数列的学习,有利于增强学生发现规律、描述规律和应用规律解决问题的意识,将一般的递推关系转化为“等差、等比”的关系,化归为等差、等比数列模型,增强利用等差、等比数列的通项和性质解决问题的能力,提升学生的数学建模能力,理解数列的函数本质.

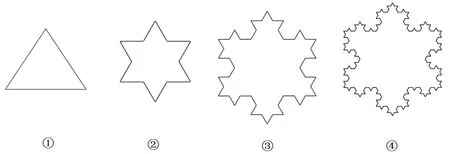
案例(2022 湖北八市联考)2022 年北京冬奥会开幕式中,当“雪花”这个节目开始后,一片巨大的“雪花”呈现在舞台中央,十分壮观. 理论上,一片雪花的周长可以无限长,围成雪花的曲线称作“雪花曲线”,又称“科赫曲线”,是瑞典数学家科赫在1904 年研究的一种分形曲线. 如图是“雪花曲线”的一种形成过程: 从一个正三角形开始,把每条边分成三等份, 然后以各边的中间一段为底边分别向外作正三角形,再去掉底边,重复进行这一过程. 若第1 个图中的三角形的周长为1,则第n个图形的周长为若第1 个图中的三角形的面积为1,则第n个图形的面积为

评析此题由苏教版高中数学选择性必修第一册第149页“探究·拓展”第17 题改编而来,试题以2022 年北京冬奥会开幕式中的雪花为素材设计真实情境,既考查等比数列及求和的相关知识和从资料中提取信息的能力,又突出数学的真、善、美. 学生试题解答的关键是将图形的分形过程理清楚,探寻图形边数、边长的变化规律,将问题化归为求等比数列的通项与等比数列的和来解决. 学生在试题求解的过程中,了解数学分形理论,感受数学的文化价值,体会数学应用的广泛性,提升了自身的数学阅读、信息提取、数学建模和数学应用能力.

2.2 以思想为线,把握数学本质

方法一般是指为获得某种东西或达到某种目的而采取的手段与行为方式,解题方法的灵活应用客观反映了学生数学解题能力与数学素养水平. 在高中数学中,同构可定义为相同的结构[4]. 同构法不仅体现了数学知识的统一性、对称性、和谐性,而且运用同构法解题能够培养学生发现规律、运用规律的化归思维能力.

运用代数的方法研究平面几何图形的性质及它们的位置关系是解析几何的本质,代数方法的灵活运用程度反映了学生的数学运算素养水平. 同构法在解析几何运算中可以起到化繁为简的良好效果.

案例(2022 年南通二模)已知双曲线=1(a ＞0,b ＞0) 的左、右焦点分别是F1,F2,P(x1,y1),Q(x2,y2)是双曲线右支上的两点,x1+y1=x2+y2=3. 记ΔPQF1,ΔPQF2的周长分别为C1,C2,若C1-C2=8,则双曲线的右顶点到直线PQ的距离为

评析此题由苏教版高中数学选择性必修第一册第19页“探究·拓展”第13 题改编而来,结合双曲线的定义,灵活选择同构法简化运算,解决问题的意识,特别突出了化归思维能力的考查. 学生试题解答的关键是利用几何图形关系将两个三角形ΔPQF1,ΔPQF2的周长之差转化为双曲线定义应用问题,将等式x1+y1=x2+y2=3 化归为确定一条直线的基本量“两个点”,利用同构的方法即可得到经过P,Q两点的直线方程为:x+y= 3,最后利用点到直线距离公式即可求得答案. 学生在试题求解的过程中,感悟数学概念和原理的重要性,正如李邦河院士所讲“数学玩的是概念,而不是纯粹的技巧. ”

2.3 以素养为本,培育高阶思维

弗利德曼曾指出:“数学的逻辑结构的一个特殊的和最重要的要素就是数学思想. 整个数学科学就是建立在这些思想的基础上,并按照这些思想发展起来的[5].”数学思想是数学的灵魂,是对数学事实与数学理论的本质认识,是数学文化的核心,没有思想就没有文化[6]. 数学试题千变万化,但是数学思想在解题过程中起着统领全局的作用. 华罗庚先生就曾对数形结合思想赋诗一首:“数与形,本是相倚依,焉能分作两边飞. 数缺形时少直觉,形少数时难入微. 数形结合百般好,割裂分家万事非. ”

圆锥曲线通过改变平面与圆锥轴的夹角,得到不同的截面,截面与圆锥面的交线可以得到椭圆、双曲线和抛物线. 圆锥曲线由一个圆锥面被平面所截这一基本图形统领全局,而用坐标系和方程思想研究圆锥曲线的几何性质,体现了数形结合思想和方程思想在研究平面几何曲线性质的基本路径,体现了方程思想串联“曲线概念—几何图形—建坐标系—求解方程—研究性质”的知识体系和数学模型建构过程.

案例如图, 在棱长为1 的正方体ABCD-A1B1C1D1中,P为棱A1B1的中点,点Q在侧面DCC1D1内运动,下列结论正确的是( )

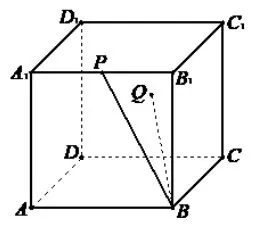
A. 若BQ⊥A1C,则动点Q的轨迹是线段;

B. 若|BQ|=√则动点Q的轨迹是圆的一部分;

C. 若∠QBD1=∠PBD1,则动点Q的轨迹是椭圆的一部分;

D. 若点Q到AB与DD1的距离相等,则动点Q的轨迹是抛物线的一部分.

评析此题借助立方体,重点考查学生的空间想象能力、逻辑分析能力,将问题化归为平面截空间几何体,截面与空间几何题表面交线问题,涉及到面面相交、平面与球面相交、平面与圆锥面相交等交线的形状判断,充分体现了学生的综合能力和数学核心素养水平.

综合法分析由于经过点B作已知直线AC1的垂线构成一个平面BC1D(三垂线定理), 因此平面BC1D与侧面DCC1D1的交线DC1即为动点Q的轨迹; 由于空间内到点B的距离为定值的点是一个球面, 因此球面与侧面DCC1D1的交线是圆, 动点Q的轨迹是该圆的一部分;由于经过点B与直线BD1夹角(cos ∠PBD1=)相等的直线构成一个以BD1为轴的圆锥面, 侧面DCC1D1与轴BD1的所成角(∠BD1C)的余弦值为,由于∠BD1C小于∠PBD1,因此圆锥面与侧面DCC1D1的交线是双曲线, 动点Q的轨迹是该双曲线的一部分; 过点Q分别作DD1,DC的垂线交DD1,DC于点M,E, 过点E作BC的平行线交AB于点F, 则QM,QF分别为点Q到直线DD1,AB的距离,由QM=QF=可得动点Q的轨迹是双曲线的一部分.

分析法分析通过建立空间直角坐标系易判断选项A,B 是正确的,选项D 是错误的;对于选项C,得到的方程是一般的二次曲线,则需要通过换元化简得到双曲线的标准方程,因此也是错误的.

3 化归思维的微专题教学思考

数学化归思想的发展,就是数学模型化的思想[7]. 化归思维是解决数学问题常用的思维方式之一,体现了数学模型化的思想. 微专题将具有紧密相关性的知识或方法化归成一个专项课题,可以有效促进学生的深度学习,加深对数学本质的理解,提高自身的数学思维能力,提高自身的数学素养.

借助化归思维设计微专题复习,将试题的考查内容回归到课本基本概念和原理,有利于提高学生阅读教材的主动性,加深数学知识的理解;将试题的考查方法化归为统一的解法,以点带面、多题一解,有利于提高学生解题方法的熟练程度,感悟知识的内在联系;让学生在知识的学习中,感悟数学思想的统领性,深化问题的理解深度和广度,培养学生综合分析问题的能力,发展学生的数学素养.

化归思维视域下的微专题教学有利于提高高考复习效率和解题训练的针对性, 让学生在数学思想主线的统领下,突破思维障碍,强化技能方法,实现以点带面,专项针对性训练,在解题的过程中训练思维,深化理解,提升数学素养. 数学微专题的选题原则应体现基础性、思想性和发展性,符合学生的认知规律和心理发展规律. 微专题教学是习题课的一种类型,数学习题课教学应着眼于数学核心素养选题,注重学生思维能力培养[8],让学生在复杂的情境中展现思维、交流表达、合作探究,优化自己的思维,创造性地解决问题.