HPM 视角下解密杨辉三角与二项式系数的关系
2023-08-07广东省汕头市聿怀中学515000曾祥荣
广东省汕头市聿怀中学(515000) 曾祥荣
1 引言
数学史与数学教育(HPM)流传较广、影响较大,深受一线教师的喜爱与关注. 目前,融入数学史的教育实践和教学设计层出不穷,但关于中国数学史融入课堂教学的研究并不多见. 杨辉三角是我国数学家的杰出成果之一,也是流传较广的数学史料,其教育价值不可忽视. 通过解密杨辉三角与二项式系数的关系,能揭示二项式系数的变化规律与众多性质. 因此,杨辉三角是不可多得的集文化魅力、数学趣味、德育功效于一体的理想教学材料.
该内容是在选修2-3“二项式定理”一节的基础上,参考教科书中“探究与发现”环节关于杨辉三角的一些“秘密”而设计的一个研究性课题, 旨在探讨和研究杨辉三角的性质,展现二项式系数的性质. 通过观察、分析、猜想、证明从而发现与杨辉三角有关的数字规律.
2 解密模式
2.1 创设情境,引入课题
首先, 简单介绍与杨辉以及杨辉三角有关的历史故事.杨辉是我国古代数学家,其主要贡献如图1,出现在其著作中并注明了该图出自北宋数学家贾宪的著作,所以“杨辉三角”实际上为“贾宪三角”. 但由于后者已失传,故今人习惯以前者称之.

图1 杨辉三角图示

图2 横向观察

图3 斜向观察
通过简要介绍杨辉三角的数学史,以数学为背景进行德育,并以此为切入点,激发学生探究杨辉三角的积极性.
2.2 合作交流,揭示性质
(1)探究杨辉三角与二项式系数的关系
计算(a+b)n(n= 0,1,2, …)展开式中的二项式系数,并将其列出,再将二项式系数与杨辉三角中的数字进行比较,尝试发现结论: 杨辉三角的第n行是(1+1)n展开的二项式系数,即
(2)横向观察
注意观察方法,即结合二项式系数,横看、纵看、斜看,从多种角度观察. 可得以下性质:
性质1 (对称性)每一行中,与首末两端“等距离”的两项的二项式系数相等,即
性质2 杨辉三角第n行数字的和等于···+=2n.
性质3 杨辉三角的每一行中奇数项的和等于偶数项的和,即=2n-1.
(3)纵向观察
观察上下相邻行数字之间的规律, 例如: 2 = 1 + 1,3=1+2,4=1+3,6=3+3,5=1+4,10=4+6……,可以得到性质4.
性质4 每一行的两端都是1,其余每个数都等于它“肩上”两个数的和,即
(4)斜向观察
引导学生“斜”向观察,例如: 1+1+1+1+1+1=6,1+2+3+4+5=15,1+3+6+10=20,1+4+10=15,归纳可得:
性质5 一般地, 在第m条斜线上(从右上到左下) 前n个数字的和, 等于第m+ 1 条斜线上的第n个数. 即
接着,我们继续换一角度“斜”向观察,如图4. 进一步地,如果换个角度再次斜向观察又会发现什么奇妙的数字特点呢? 让学生观察图4 中各斜线上数字之和,算出前9 条斜线甚至更多斜线的结果.
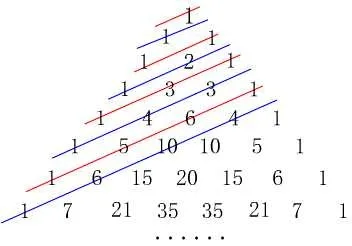
图4 “斜”向观察
1, 1, 2, 3, 5, 8, 13, 21, 34,···, 此数列{an}满足an=an-1+an-2(n≥3).
性质6 从第3 条斜线起,其后各斜线上各数字的和都是前两条斜线数字之和的和.
至此,学生在教师引导下已经完成对杨辉三角全方位的观察,目的在于培养学生的观察能力,以及由特殊到一般的归纳、猜想能力. 同时,在讲授过程中,给学生足够的探索时间,引导学生推广再得出一般性的结论.
2.3 应用举例,提升能力
如图5 所示,在杨辉三角中,斜线上方箭头所示的数组成一个锯齿形的数列: 1,2,3,3,6,4,10,5,,记这个数列的前n项的和为S(n),则S(12)的值是多少?

图5 综合观察
通过这一思考题,让学生学以致用的同时自我反思学习结果.
2.4 归纳小结,总结提升
本节重点在于掌握二项式系数的基本性质与杨辉三角的实际应用,同时使学生的数学思维得以提升. 但能否再继续拓宽思维层面呢? 可以尝试引导学生思考以下三个问题:
问题1 在杨辉三角中,除了本节课发现的性质外,你还能再找出其它的一些性质吗? 与其他同学交流探讨.
问题2 查阅有关杨辉三角与斐波那契数列实际应用的资料并与同学交流学习.
问题3 “纵横路线图”问题: 图6 是X 城市的部分街道图,

图6 X 城市街道图
(1)若从点A处走到点B处(注意只能由北到南,由西向东),则有几种不同的走法? 若纵横各四条路又有多少种走法? 有何规律?
(2)把图顺时针转45°,如图6 中右图所示,在交叉点标上相应的杨辉三角数. 点B处的杨辉三角数与A到B的走法有什么关系?
最后,与学生共同总结,引导学生探究杨辉三角与斐波那契数列之间的联系.
3 总结与启示
HPM 视角下的二项式系数的教学是一个比较有文化味的角度,相比其他的教学视角,更具文化底蕴、历史深度和数学思维. 这一教学实践能为今后的高中数学教学带来“五个一”的启示.
一次溯源,在HPM 视角下,将学生带回杨辉时代,想象与数学家对话,同杨辉一齐探究二项式展开式的性质,并通过数学史的学习掌握二项式展开式系数的相关性质,做到帮助学生追本溯源,真正理解概念的形成与发展,而不是仅靠死记硬背. 一种提升,通过联系函数的图象和相关性质探究证明二项式系数的性质,加深不同知识间的联系,有利于帮助学生形成连贯一体的知识体系,提升对知识的把握. 一个高度,通过数形结合、归纳思想,以及教师引导、学生探究的教学方式,培养学生数学思维,促进学生学以致用,将课堂成果落实到数学思想的培养高度. 一堂德育,“杨辉三角”是我国古代数学史上重要的成就之一,彰显了我国古代数学家的孜孜不倦和聪明才智,这一内容能让学生认识到除了西方欧氏几何之美,更有东方演算之美.
总而言之,数学中蕴含的美是深广博大的,不仅有对称美,还有简洁美、和谐美等. 数学教学中从来不缺乏美,而是需要发现美的视角.
