核心素养背景下高三数学课堂教学现状及对策分析

江苏省高淳区教师发展中心(211300) 夏继平

核心素养背景下的新高考已经进行了2 年了,不同于前两年的老教材新课标、新高考,今年是新教材、新课标、新高考,因此可以说是全面进入新高考评价时代了. 笔者近期对区内3 所高中的课堂教学进行了调研,听课34 节,参加集体备课及研讨6 场,个别交流20 多次,感想颇多,特撰文总结如下:

1 课堂教学现状

1.1 课程标准无人关注

虽然3 所学校都在使用导学案进行课堂教学,并在导学案的第一个环节标注了本节课的课标要求,但在课堂教学或集体研讨的过程中没有人关注,甚至有部分教师连打印在导学案上的课标要求都说不清楚,仅凭题目或经验在教学,完全没有意识到新课标要求的变化. 更别说数学核心素养表现的6 个关键词及相关的说明了.

1.2 教学目标云山雾绕

在听课和研讨的过程中,教师普遍缺乏课堂教学目标的设定,给出的理由是班级学生层次差异明显,不好作统一的要求;还有就是研讨时间不足,不能集中研讨每节课的教学目标设定. 从而导致教学目标的设定变成了教师个体的一种感觉,所不同是少数优秀教师的感觉好一点而已.

1.3 知识梳理千篇一律

一轮复习的知识梳理部分,一般是学生课前预做,教师课堂教学时通过讲解、问答、板演、投影等手段完成. 教师普遍缺乏对知识梳理教学的深加工,学生只是简单的过了一遍,会的同学纯属浪费时间, 差的学生只是简单的回顾了一下,没有形成系统的理解认识,过几天又会遗忘. 课间交流,教师只会评价学生差,这么简单的知识都记不住,没法教. 然后就是不断抱怨,自习课去不断强调. 循环往复,苦不堪言.

1.4 基础训练定位不清

导学案的基础训练部分,一般是学生课前预做(也可当堂限时完成). 本该是检测学生基本知识情况的基础训练,却由于备课研讨不充分, 变成了难度较大的规律性提炼问题,与例题功能含混不清. 导致本该5 分钟点评就能结束的环节,却常常要用20 分钟,甚至30 钟才能解决. 一节课就完成一个基础训练在很多课堂是常见行为.

1.5 例题教学规律不显

由于前面的课前热身占据了大量时间,例题教学显的非常仓促,有时根本没有,有的也仅仅是完成任务,缺乏规律的总结与提炼. 少数能完成例题教学的教师,也是一道接一道的机械完成,例题间的衔接及功能基本没有体现,学生思考感悟的时间太少,基本是拖着学生走,大量学生例题学习的获得感低.

1.6 反馈作业针对不强

导学案的反馈练习设计几乎没人关注,且不说题目质量,里面错题、重题时常发生. 刨去错题、重题,剩下的题目要么难度过大,要么与课堂教学的相关性低,层次目标不明显,针对性不强. 多数学生需花了大量时间,常讨论、抄袭、搜索答案才能解决,加之各种午练、周练挤占,部分同学甚至不交作业. 另一方面,上述低效作业导致教师需花大量时间讲评,课时不够,就晚自习讲,挤占学生作业时间,致使学生作业无法自主完成,更谈不上自主整理. 形成恶性循环,教师大喊苦累,却又不愿改变作业布置和低效讲评的现状.

2 例谈对策分析

针对上述现状,笔者依据格兰特×威金斯和杰伊×麦克泰格的逆向设计理论,并结合自己多年的高三教学经验,以下面一节高三一轮复习课“平面向量的概念及线性运算1”来试说对策分析.

2.1 课标研读指明方向

新课程标准的核心素养要求是教师教学行为的总纲,需要教师认真研读,理解其核心理念与思想,并在课堂教学中加以渗透. 新课标中标明,向量属于几何与代数主题. 突出几何直观与代数运算之间的融合,即通过形与数的结合,感悟数学知识之间的关联. 在向量概念部分明确要求理解平面向量的意义和两个向量相等的含义,理解平面向量的几何表示和基本要素;借助实例分析,掌握向量加法、减法及运算规则,理解其几何意义;通过实例分析,掌握平面向量数乘运算及运算规则,理解其几何意义;理解两个平面向量共线的含义.对向量的概念部分课标描述的已经非常祥尽了. 我们几乎只要照搬就能确立一节课的教学目标.

2.2 逆向设计教学目标

根据课标要求,以及逆向设计的三个阶段: 确定预期结果、确定合适的评估证据、设计学习体验和教学,确定如下教学目标: 1. 通过平行四边形案例分析,理解两个向量相等的含义,平面向量的几何表示和基本要素;掌握向量加法、减法及运算规则,理解其几何意义;掌握平面向量数乘运算及运算规则,理解其几何意义;理解两个平面向量共线的含义. 2.通过课前热身的练习,学生评估目标1 的达成情况. 3. 通过例题的学习,深度参与向量的线性运算,能够掌握研究图形与图形、图形与数量之间关系基本方法,能够借助图形性质探索数学规律(直观想象水平二). 4. 通过练习及学生评价,学生评估目标2 的达成情况. 5. 学生根据课堂表现,制定学习计划,教师布置个性化分层作业.

2.3 变换方式知识梳理

高三一轮复习的知识梳理是必要的. 但不能是简单的新课重复,需起到弥补漏洞和提升整合的作用. 通过知识梳理,要让学生对知识的结构越来越清晰,机械记忆的东西越来越少,直观想象和数学运算的素养逐渐提升. 具体设计如下:

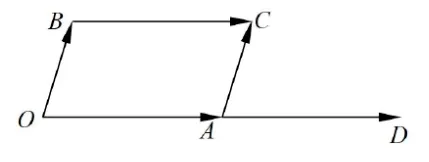
问题1 已知四边形OACB为平行四边形, 且OA=AD, 请指出右图中的相等向量? 并说明原因. (完成目标1.)

问题2 请在右图中作出(完成目标1.)

问题3请写出与0,与呢? (完成目标1.)

设计说明: 几何直观水平一提到能够在熟悉的数学情境中描述简单图形的位置关系和度量关系及其特有性质. 因此学生在思考解决上述问题的时候,教师在数与形的关系上加以引导,则相对与传统的知识讲授式教学对学生几何直观素养提升会起到事半功倍的作用.

2.4 基础训练检测效果

1. 下列四个命题中,正确的是( )

A. 若a//b,则a=b

B. 若|a|=|b|,则a=b

C. 若|a|=|b|,则a//b

D. 若a=b,则|a|=|b|

2. (多选)下列说法正确的是( )

A. 非零向量a与b同向是a=b的必要不充分条件；

C.a与b是非零向量,若a与b同向,则a与-b反向；

D. 设λ,µ为实数,若λa=µb,则a与b共线.

3. (多选) 如图所示, 在ΔABC中,D是AB的中点, 下列关于向量表示正确的是( )

设计说明: 基础训练是对向量基本知识、基本方法的检测,适合各层次学生,教师可针对学生答题情况作必要的点评,方法归纳时要引导学生学会从图形上分析. 让学生体会几何直观的作用和意义.

2.5 例题教学提炼规律

例1 已知O,A,B三点不共线, 且

(1)若m=n=12,求证:A,P,B三点共线;

(2)若m=13,n=23,求证:A,P,B三点共线;

(3)若m+n=1,求证:A,P,B三点共线;

(4)若A,P,B三点共线,求证:m+n=1.

变式练习: 如图,在直角梯形ABCD中,则2r+3s=( )

A. 1 B. 2 C. 3 D. 4

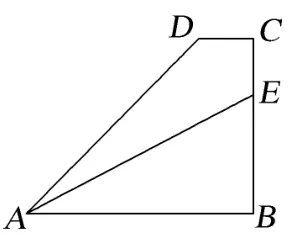
设计说明: 例题1 不给图, 目的是引导学生根据基础训练中的图形铺垫自己作图分析. 4 道小题层层推进, 引发学生思考提炼规律. 层次高的学生可独立完成,板书解答过程,同时教师要求他们思考为什么要有这样的问题,引导他们把向量共线、定比分点、加减法运算在最基础的三角中结合起来. 发展他们通过直观想象提出数学问题,用图形探索解决问题的思路的素养,加深对数形结合的思想认识,进一步体会几何直观的作用和意义.对于层次一般的学生教师可在巡堂的时候启发他们解决问题,并采用合作交流或学习优秀同学的板书过程来完成问题,并尝试总结提炼规律. 对于层次较低的学生,教师可采用个别辅导、合作交流、观看板书的方式完成问题,并指导他们尝试理解规律. 变式练习是例1 规律的应用检测, 引导学生把一般几何图形转化为三角形,然后在三角形中利用向量运算解决问题,起到检测巩固规律的作用. 逆向设计理论要求教学设计要从确定的预期结果出发,因此,若时间够用可再配少量几何图形类向量问题,进一步检测学生的学习目标达成情况,为后面的反馈作业做准备.在依据逆向设计理论进行渗透核心素养的教学设计中,一定要关注不同层次学生的学习需求. 以人为本,精巧构思,灵活教学应是新课标要求下教师教学的应有之义.

2.6 反馈作业精准定位

反馈作业前面设置4 道面向全体学生的关于向量基本概念、基本运算的基本题,从略.若

5. 在ΔABC中,点M为AC上的点,且则λ-µ的值是()

6. 在平行四边形ABCD中,E,F分别为边BC,CD的中点,若则

7. (多选)设点M是ΔABC所在平面内一点,则下列说法正确的是( )面积是△ABC面积的

第5 题是例1 规律的简单变式应用,非常适合层次较低的学生提升描述简单图形的位置关系和度量关系及其特有性质的直观想象素养水平一. 第6 题是对学生把一般图形化归为三角形解决能力的检测,属于研究图形与图形、图形与数量之间关系的基本方法,能够借助图形性质探索数学规律的直观想象水平二的表现. 第7 题是对例题规律的多角度、多知识联合考查,检测高层次学生的作图分析能力,属于能够通过想象对复杂的数学问题进行直观表达,反映数学问题的本质,形成解决问题的思路的直观素养水平三的表现. 作业设计可以说是逆向设计理论的评估证据,学生的学生检测结果可作为下节课教学目标、学习目标、作业目标的设计依据,形成教育教学闭环,滚动前进. 同时教师需针对不同层次的学生指导他们根据课堂学习所暴露出来的问题或成功的规律感悟,结合自身素养特点和核心素养的表现关系,制定适合自己素养提升的个性化学习计划或作业.

最后,高三教学面临高考要求,社会关注度高,学生家长期盼强烈,这是高三教师不可回避的压力. 作为一名高三教师,面临教学质量压力时不能使蛮力,大量布置作业,或消极怠工,把责任推给学生. 应勇担责任使巧力,加强课程目标、教学目标、学习目标、作业目标——四维目标的研究,学会从各层学生视角出发,进行逆向设计教学. 做到“心中有人,心中有标,手中有术”,以适应核心素养要求下的新课标教学.