基于CNN-LSTM的晶圆良率预测*

吴立辉,周 秀,张中伟

(1.河南工业大学机电工程学院,郑州 450001;2.上海应用技术大学机械工程学院,上海 201418)

0 引言

半导体产品制造过程涉及晶圆制备、晶圆制造、芯片封装测试等主要阶段,其中晶圆制造是半导体制造企业资金、技术、人员投入最为密集的关键环节。在晶圆制造最后阶段,需对已完工产品进行晶圆允收测试(wafer acceptance test,WAT),以此对晶圆片是否合格验收进行决策判断。WAT过程需对集晶圆片大量电路采集各类电测参数,形成大规模测试数据。基于WAT数据分析测试电路参数与晶圆良率之间的关联,进而对晶圆良率进行预测,可揭示半导体工艺制程中影响晶圆良率的关键环节,为工艺制程调整及晶圆质量控制提供重要参考。因此,晶圆良率预测逐渐获得晶圆制造质量管理部门关注。

传统晶圆良率预测研究主要考虑晶圆缺陷的数量、类型、来源等因素展开,BAE等[1]考虑晶圆缺陷的群聚特征与晶圆图上缺陷的空间分布特点,基于不同的回归分析方法建立良率预测模型;邱明辉等[2]提出一种基于密度噪声的应用空间聚类方法分析晶圆缺陷的聚集特征,并设计一种混合模糊支持向量机模型来预测晶圆良率;DONG等[3]基于划痕图案的空间模式预测晶圆良率,并探究分析影响良率的晶圆制造工艺原因。以上研究基于晶圆缺陷数据构建预测模型实现良率预测,其预测精度及稳定性欠佳,且无法据此对晶圆加工工艺或参数进行改进。

随着大数据技术发展,对WAT数据进行挖掘分析并构建电性测试参数与晶圆良率的非线性映射函数关系,逐渐成为研究热点。RAVI等[4]通过主成分分析方法(principal component analysis,PCA)实现WAT数据的特征提取和维度缩减,进而构建回归预测模型完成良率预测,而PCA导致部分关键信息丢失,准确性不足。CHIEN等[5]通过专家经验进行高相关电性参数的筛选,并提出基于改进偏最小二乘法的预测模型,然而,该模型的预测精度取决于专家的专业素养。JIANG等[6]混合互信息法和递归消除特性法对WAT数据进行处理,并基于高斯混合模型构建加权集成回归器实现良率预测。许鸿伟等[7]提出一种改进的深度信念网络(deep belief network,DBN)预测模型,首先使用PCA提取关键参数,并通过训练改进的深度信念网络构建模型。目前相关研究主要从关键特征提取和预测模型构建两方面进行。由于高维WAT参数存在相关性、冗余性等特点,现有特征处理方法无法识别所有关键参数,导致部分关键特征丢失,降低预测准确性。此外,由于晶圆成批投料加工特性,相邻晶圆之间在加工工艺、加工参数等方面具有相关性,而现有预测模型未考虑WAT样本数据间的相关特性,影响晶圆良率预测精度。

针对上述问题,本文提出基于卷积神经网络和长短期记忆网络集成模型的晶圆良率预测方法。该方法将原始数据进行预处理后输入至模型中,利用深度学习的卷积神经网络实现关键特征的识别,考虑相邻晶圆间的时序相关性,设计长短期记忆网络进行回归分析,以此挖掘晶圆允收测试参数与晶圆良率之间复杂的关系,实现准确的晶圆良率预测。

1 晶圆良率预测问题

半导体制造各个阶段均会因异常缺陷导致最终晶圆产品失效,良率是量化失效的重要指标,也是晶圆制造企业最为关注的核心指标。良率根据晶圆不同加工阶段,通常分为晶圆良率、晶粒良率和芯片封测良率,晶圆良率是指晶圆制造阶段完成所有工艺步骤后晶圆片中没有缺陷且满足性能要求的芯片比率[8],晶粒良率和封测良率分别为封测前期与末期所有测试为合格晶粒占所有晶粒的比值。良率越高,同一片晶圆上产出的合格芯片数量就越多,晶圆厂的效益越显著。晶圆制造阶段因工艺步骤繁多、工艺制程复杂,成为影响良率的关键环节,其也是本文晶圆良率预测研究关注的阶段。

WAT也称工艺控制监测(process control monitor,PCM),是晶圆制造阶段的一个关键站点(如图1所示),其内容为在晶圆产品流片结束后测量整个晶圆片特定结构的电性参数,如阈值电压、源漏击穿电压、GOI电性厚度、通孔接触电阻、金属击穿电压等,进而检测晶圆片产品的工艺情况,评估半导体制造过程的质量及稳定性,判断晶圆是否符合实际验收要求。WAT参数可反馈生产线的实际生产情况,但WAT参数众多、部分参数之间冗杂度高、相关性强,与晶圆良率之间关系复杂,难以建立两者之间的非线性复杂映射函数。此外,晶圆加工过程通常以晶圆卡(25片晶圆装入一个晶圆盒,称为晶圆卡或晶圆Lot,其是晶圆加工与搬运的基本单元)为单位进行,晶圆卡内的晶圆加工工艺、加工参数、加工设备具有强相似性;同时,半导体制造过程中采用run-to-run策略[9],工程师会参考前一卡晶圆加工数据参数,对下一卡晶圆加工参数进行调整,从而晶圆WAT样本数据间具有明显的时序相关性,而普通的神经网络未考虑输入参数间的关联,数据的处理在各个时刻相互独立[10]。

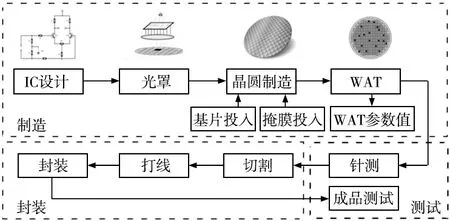
图1 半导体制造流程示意图

因此,考虑以上特性研究基于WAT参数与晶圆良率之间的映射关系,建立精准的晶圆良率预测模型,对有效监测晶圆制造阶段生产线情况、调整工艺制程及控制晶圆质量等均至关重要。

2 基于CNN-LSTM的晶圆良率预测模型

基于CNN-LSTM的晶圆良率预测方法框架如图2所示。首先,针对晶圆厂实际生产加工时晶圆允收测试过程采集的数据集具有杂乱性,存在电测参数数据部分缺失、电测参数异常点、数据量纲不一致等问题,对收集到的晶圆允收测试数据进行数据预处理;其次,针对输入数据的参数高达几百个,某些参数对晶圆良率的影响效果基本一致、部分参数对晶圆良率影响甚微的特点,设计卷积神经网络层对数据的关键特征进行识别;再次,针对晶圆WAT样本数据间的时序相关特性,以及晶圆加工通常以晶圆卡为单位进行的特点,设计长短期记忆网络层进行晶圆良率的回归预测,从而实现晶圆良率准确预测。

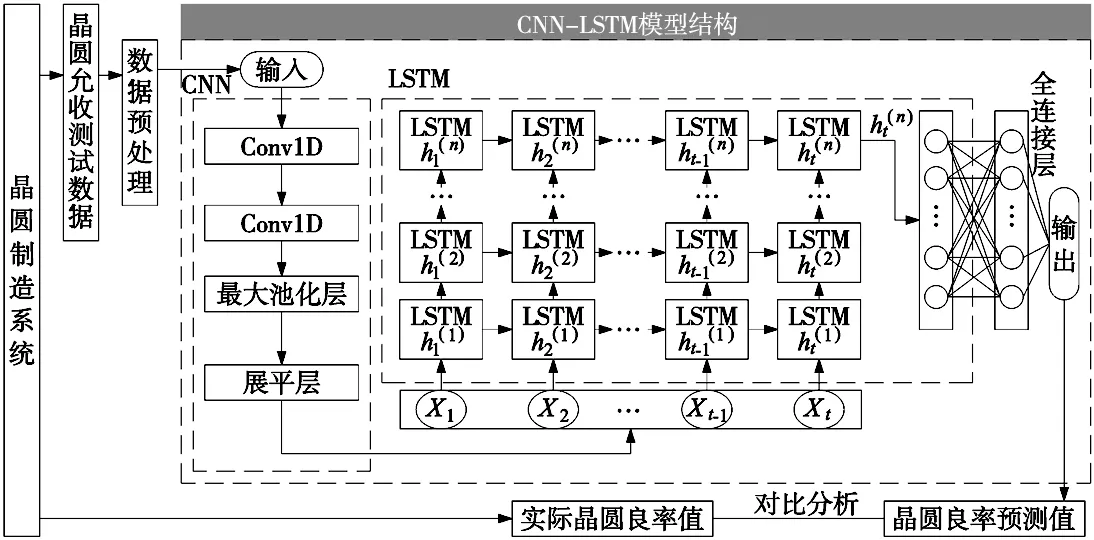
图2 基于CNN-LSTM的晶圆良率预测方法框架

2.1 WAT数据预处理

针对实际晶圆允收测试过程中采集数据存在的电测参数数据部分缺失、电测参数异常点、数据量纲不一致等问题,WAT数据预处理具体方法如下。

(1)电测参数数据部分缺失处理。对采集的数据进行统计学分析,针对某参数列缺失值大于50%的情况,因其影响数据的准确性、可靠性,直接将其剔除处理。针对仅存在少数缺失的参数列,采用最近邻插补法(k-nearest neighbor,KNN)[11]对缺失值进行填充,缺失数据插补过程中,缺失位置数值根据其特征空间内相邻最近的K个观测值决定。

(2)电测参数异常点处理。数据中存在的异常值会干扰模型的训练过程,降低准确度,常见的异常值处理方法有:通过对属性值进行描述性统计的统计分析法、统计数据分布的3δ原则法以及通过百分比计算统计分析的箱型图法[7]。由于箱式图可直观表现出数据分布的情况,且不受数据分布的限制,故针对电测参数异常点,通过绘制箱式图筛选出WAT参数中的异常值,并进行剔除,减小数据的噪声。

(3)电测参数量纲不一致处理。考虑到晶圆电性测试阶段各项参数之间的量纲不一致问题,将值在不同范围内的WAT参数采用最大-最小值归一化处理,将原始值通过线性转换的方式量化到0～1之间,其数学表达式如下:

(1)

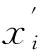
2.2 CNN模型设计

CNN通过使用滤波器系数与输入数据进行卷积,后经压缩、特征归一化处理等一系列操作,再通过不同的网络层次进行传递,可获取层间关系和空域信息[12],因此可从数据集众多特征中提取关键特征甚至潜在特征。卷积神经网络由两层卷积层和池化层交替叠加而成,输入参数与初始化的卷积核卷积得到对应的特征向量集,在神经网络的传播过程中初始卷积核不断迭代更新,从而识别输入参数中的关键特征,降低数据冗杂度,但因其滑动卷积的计算方式仅对识别局部特征有优势,故结合池化层提取全局特征,使识别的特征既包含局部信息又包含全局信息,同时在每个卷积层与池化层之间都设有激活函数用以加速模型的收敛,输入参数经过卷积神经网络的处理后,将所有特征融合并通过卷积神经网络重新生产新的关键特征。

CNN层设计包括一个将输入变量重新接受为输入的输入层,一个向LSTM提供输入特征的全连接层,以及一定数量的隐藏层。隐藏层通常由卷积层、激活函数和池化层组成。CNN层能够通过卷积层从高维的输入层中获得局部特征,并将其传递到下层,并通过最大池化层获得更复杂的全局特征[13]。第l层卷积层的输出向量y如式(2)所示:

(2)

式中:x为输入向量,b为由输入特征映射的偏置参数,W为卷积核的权重参数,m为滤波器的数量,yl-1为前一卷积层的输出向量,ReLU为激活函数,*表示卷积。最大池化层对卷积层输出进行子采样,通过消除非极大值降低上一层计算复杂度,同时能够在不同采样区域内提取局部关键特征,以持续更新为最突出的特征信息。最大池化层运算由如式(3)所示:

pl=MaxPool(yl-1)

(3)

池化层后使用展平层将数据进行维度的改变,即多维一维化,随后通过全连接层将数据重塑为LSTM所需数据类型,实现CNN层和LSTM的连接以及输入变量的传输。其次,针对输入数据的参数高达几百个,某些参数对晶圆良率的影响效果基本一致、部分参数对晶圆良率影响甚微的特点,设计卷积神经网络层对数据的关键特征进行识别;再次,针对晶圆WAT样本数据间的时序相关特性,以及晶圆加工通常以晶圆卡为单位进行的特点,设计长短期记忆网络层进行晶圆良率的回归预测,从而实现晶圆良率准确预测。

2.3 LSTM模型设计

LSTM是一种新型循环神经网络,其通过引入记忆单元与一系列门控状态解决由于隐藏单元状态的长距离传输而带来的梯度爆发与梯度消失问题[14],相较于其他的神经网络,LSTM用记忆单元代替传统神经网络隐藏层节点,每个记忆单元由遗忘门、输入门、输出门3种门控状态控制信息的传递,故LSTM具有存储和反馈功能,能捕捉到输入数据中的关键信息,长期保留以传递至下一状态单元,并根据信息关键程度不断调整权重,解决传统神经网络存在的长期依赖问题,准确挖掘数据中的重要信息。其记忆单元架构设计如图3所示。

图3 LSTM记忆单元架构

LSTM当前输入xt与上一状态传递下来的ht-1运算后得到4个状态,分别为遗忘门ft、候选记忆值向量Ct、输入门it、输出门ot。ft、it、ot是由运算向量乘以权重矩阵后,通过Sigmoid激活函数将其转换成0～1的数值,从而作为一种门控状态;Ct则是通过tanh激活函数将结果转换为-1～1之间的值,仅将其作为输入数据,不控制信息的传输;单元状态信息的传递由上述的“门”进行控制,若“门”的状态值为1,则保留当前单元状态的所有信息,若状态值为0,则全部遗忘。遗忘门用以控制丢弃上一状态的何种信息,输入门决定何种新信息将被存储于细胞单元,输出门确定输出信息,此输出信息基于遗忘门和输入门的信息,但还需进行进一步处理。ft、it、Ct、ot的定义如式(4)～式(7)所示:

ft=σ(Wfhht-1+Wfxxt+bf)

(4)

it=σ(Wihht-1+Wixxt+bi)

(5)

Ct=tanh(WChht-1+WCxxt+bC)

(6)

ot=σ(Wohht-1+Woxxt+bo)

(7)

式中:xt表示时间步长为t时刻的输入变量,ht表示上一时刻的隐藏状态,W表示权重参数,b表示偏置参数,σ表示一个非线性的激活函数。此外,LSTM还有两个传输单元,一个Ct(记忆单元),一个ht(隐藏单元):Ct为上一状态的传输信息与候选记忆值向量之和,传递相对稳定,变动量很小;ht由输入门和记忆单元控制,每一步都会更新,在不同节点变动量很大。两个传输单元通过门控状态更新传输单元的信息,处理后得到输出值Yt。Ct、ht、Yt更新公式为:

Ct=ft⊙Ct-1+it⊙Ct

(8)

ht=ot⊙tanh(Ct)

(9)

Yt=σ(WYht)

(10)

式中:WY为权重参数,其值由神经网络训练得到。

上层CNN提取的影响晶圆良率的关键特征通过全连接层与LSTM连接作为输入,数据经过包含若干层隐藏层的LSTM有监督回归分析处理后连接两层全连接层进行输出,将LSTM预测的数据进行扁平化处理,得到我们所需要的信息维度,输出预测晶圆良率值。此外半导体加工过程中同一批次晶圆的加工参数具有相关性,且工程师参考上一组的参数值会对下一组数据进行一系列微调,从而创建时间序列特征[15]。因此在使用输入数据时,应考虑到参数间时序相关性,故设定LSTM滑动窗口的大小为25,即以一个晶圆卡中25片晶圆的实际生产数据为指定单位长度来遍历整个输入样本数据,更为准确地挖掘WAT参数与晶圆良率之间的非线性复杂映射关系,提高良率预测精度。

3 实例分析

为验证本文提出的CNN-LSTM方法的有效性,采用上海某晶圆制造企业的WAT数据集对其进行验证。该数据集共包含16 000多片晶圆WAT信息,每片晶圆WAT包含430个电性测试参数,主要为MOS晶体管测试参数、栅氧化层的完整性测试参数、多晶硅栅场效应晶体管测试参数、方块电阻测试参数、接触电阻测试参数类等。晶圆加工通常以Lot为单位,一个Lot中包含25片晶圆,考虑到其时序性,以一个Lot的25片晶圆为滑动窗口数量进行输入。以90%的晶圆WAT数据作为训练集对CNN-LSTM预测模型进行训练,将剩下10%作为验证集,验证模型的性能。为提高预测模型拟合效果,试验过程中采用K-Fold交叉验证方式进行。为客观评估模型的有效性,采用两种评估函数以及模型收敛速度来验证模型的性能,两种评估函数分别为平均绝对误差(mean absolute error,MAE)、均方根误差(root mean squared error,RMSE),其数学表达式为:

(11)

(12)

3.1 实验参数设定

CNN-LSTM模型参数设定内容为CNN卷积层的滤波器数量、卷积核长度、激活函数、最大池化层大小、LSTM隐藏层数量等,参数调整会影响模型学习效率和性能。经过大量实验对比,选取CNN-LSTM模型参数如表1所示。其中,激活函数(activation function)是神经网络模型的一个重要内容,激活函数使神经网络中神经元具备自主学习及适应能力,而ReLU函数近似生物神经元结构,选其为网络层激活函数,相比于传统激活函数收敛速度更快,计算复杂度更低,故在CNN的可见层及LSTM中均选用ReLU作为激活函数。

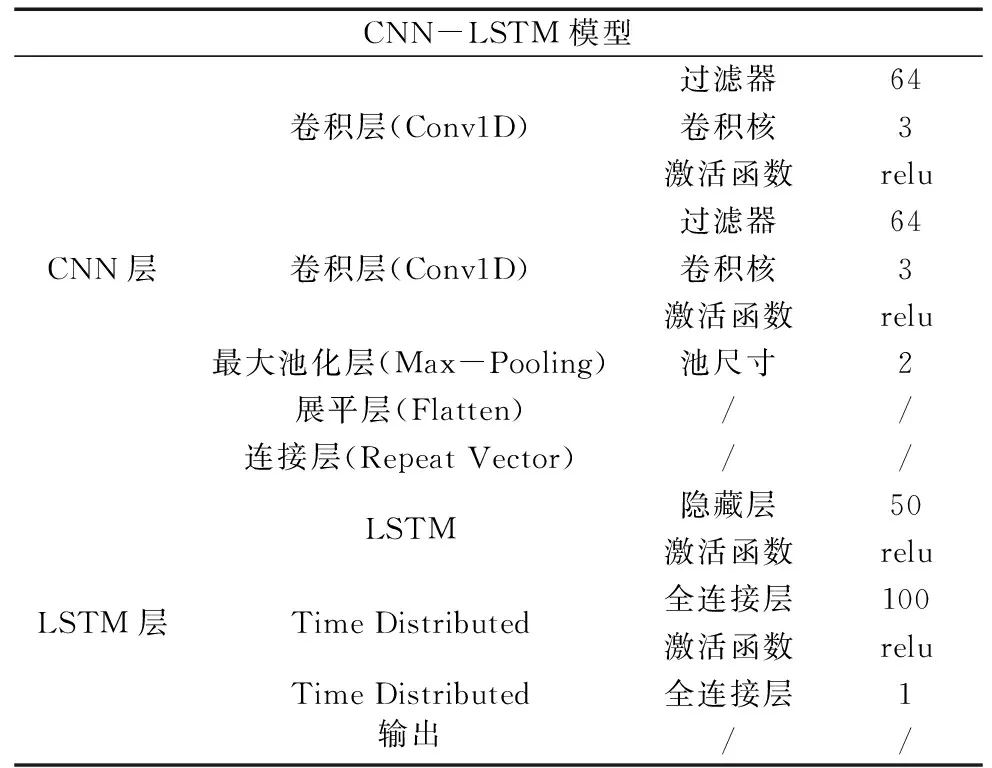
表1 模型参数设置表

在本文方法模型中,选用随机梯度下降(stochastic gradient descent,SGD)作为模型的优化算法,均方差损失函数作为模型的损失函数,设置初始学习率为0.01。此外为了减少训练参数数量并防止过拟合,设置dropout层,随机删除部分神经元。在上述参数设置情况下,选取CNN-LSTM模型全局迭代次数分别为50、70、100、150、300、500共6种情况进行实验,其损失函数、平均绝对误差、均方根误差值如表2所示。由表2可知,当模型全局迭代次数设置为150次时模型开始收敛,且晶圆良率预测精度良好,因此,选取模型全局迭代次数为150次。

表2 6种迭代次数实验结果对比

3.2 对比分析

将本文提出的CNN-LSTM模型与传统基于LSTM、ConvLSTM、BPNN、DBN的晶圆良率预测模型进行比较,比较性能指标为MAE与RMSE,试验结果如表3所示。由表3可知,CNN-LSTM、LSTM、ConvLSTM、BPNN、DBN模型的MAE分别为0.013 2、0.015 6、0.015 2、0.024 1、0.018 2,CNN-LSTM相较于LSTM、ConvLSTM、BPNN、DBN模型,MAE相对误差分别降低了18%、15%、82%、37%;CNN-LSTM、LSTM、ConvLSTM、BPNN、DBN模型的RMSE分别为0.017 5、0.022 7、0.019 1、0.021 9、0.018 8,CNN-LSTM相较于LSTM、ConvLSTM、BPNN、DBN模型,RMSE相对误差分别降低了29%、9%、25%、7%。因此,CNN-LSTM模型在MAE与RMSE指标方面优于上述传统晶圆良率预测模型。

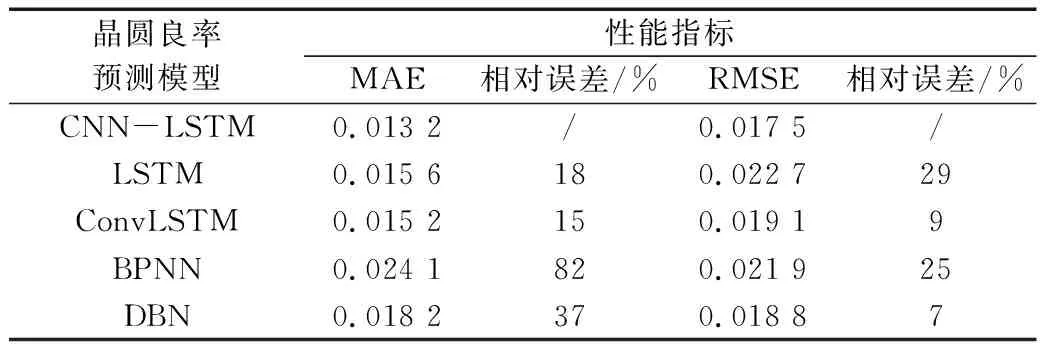
表3 CNN-LSTM预测模型与传统晶圆良率预测模型比较

随机采取5种预测模型的200组数据结果进行对比,100组数据取自训练集,100组数据取自测试集,5种模型实际值与预测值之间误差区间结果对比如图4所示。

图4 各预测模型的晶圆良率预测值与实际值相对误差区间比较

由图4可知,基于CNN-LSTM预测模型的晶圆良率预测值与实际值相对误差小于1%的比例为72.5%,而LSTM、ConvLSTM、BPNN、DBN模型的预测值与实际值相对误差小于1%的比例分别为67.1%、68.5%、55.6%、61.5%;CNN-LSTM与LSTM、ConvLSTM、BPNN、DBN模型的晶圆良率预测值与实际值相对误差位于[0,3%]区间的比例分别为96.9%、95.9%、95.6%、85.7%、96.4%。因此,相较于基于LSTM、ConvLSTM、BPNN、DBN的晶圆良率预测模型,CNN-LSTM模型的预测结果具有更好的收敛稳定性。

在此基础上,将CNN-LSTM模型与LSTM、ConvLSTM、BPNN、DBN模型的收敛速度进行比较,结果如表4所示。表4结果表明,CNN-LSTM预测模型全局迭代150次即可收敛至MAE和RMSE指标最优,分别为0.013 2和0.017 5;与之相比,LSTM、ConvLSTM、BPNN、DBN模型获得MAE和RMSE指标最优分别需全局迭代500、500、1000、4000次。本文提出的CNN-LSTM模型具有更优的收敛速度。

表4 5种模型全局迭代次数实验评估值

以上试验分析可知,本文提出的CNN-LSTM预测模型在MAE、RMSE与收敛速度指标等方面均优于传统基于LSTM、ConvLSTM、BPNN、DBN的晶圆良率预测方法,表明本文提出的CNN-LSTM方法是有效的。

4 结束语

为提高晶圆制造阶段基于WAT参数的晶圆良率预测准确性,本文提出一种基于CNN-LSTM的晶圆良率预测方法。该方法首先对WAT参数存在的缺陷进行预处理;其次将处理后的数据输入至模型中,CNN层识别WAT数据的关键特征;再次,设计LSTM层接收由CNN层传递的关键信息,描述晶圆WAT样本数据间的时序相关特性并挖掘WAT参数与晶圆良率之间的关系,实现晶圆良率的准确预测。以上海某晶圆制造企业收集的真实生产数据为验证数据,将CNN-LSTM预测模型与传统的基于LSTM、ConvLSTM、BPNN、DBN的晶圆良率预测方法进行比较,由实验结果分析可知,本文提出的CNN-LSTM预测模型在MAE、RMSE指标方面优于其他模型,表明此模型具有更高的预测准确度,同时该模型的收敛速度相较于其他模型有明显提升,表明本文提出的CNN-LSTM方法是有效的。