基于广义S变换与隐马尔可夫的滚动轴承性能评估*
2023-08-02李雯玉郑小霞
李雯玉,郑小霞
(上海电力大学自动化工程学院,上海 200090)
0 引言
滚动轴承对各种机械设备而言是不可或缺的重要组件,在工作时不仅处于高速运行状态,而且受到周期性的部件冲击,使其极易受到损害并产生故障[1-2]。一旦发生故障会影响机械设备的整体运行工作,使得安全保障埋下隐患且易造成经济成本损耗,因此滚动轴承状态监测的相关研究成为近年来的热点[3-4]。由于旋转机械传动系统工作环境的复杂性和多样性,滚动轴承故障信号往往伴随着强背景信号与噪声,并且滚动轴承的振动监测信号往往是典型的非平稳信号,比较难以准确辨别捕捉。因此,滚动轴承难以提取出有效的特征信息[5-6]。
特征指标的提取是退化状态识别的关键步骤,所提取特征指标的优劣影响着退化状态识别结果的准确性[7]。许多先进的信号处理方法已被应用于滚动轴承的特征提取[8-10]。
李恒等[11]对轴承采集到的振动信号进行短时傅里叶变换(short time fourier transform,STFT)处理后从而提取到特征指标,但是STFT无法兼顾良好频域分辨率和较高时间分辨率。GUO等[12]通过小波变换(wavelet transform,WT)得到轴承故障信号的时频图用于特征提取,但WT难以选择小波基且信号相位信息不足。WANG等[13]提出了一种基于S变换(S-transform,ST)和卷积神经网络结合的滚动轴承故障诊断方法,从而解决了STFT存在固定时频分辨率的难题;同时能维持信号的绝对相位信息;但ST的核心窗函数固定,使得ST在实际应用受到限制,广义S变换通过引入窗宽调节因子使S变换具有更高的自适应性。
在滚动轴承的性能退化过程中,是无法直接观察其状态,而是通过监测到的观测信息与隐含信息间的关系判断。该过程特性与隐马尔可夫模型(hidden markov model,HMM) 类似从而可用其来表述。WANG等[14]使用HMM模型对数据样本进行分类用于故障检测,证明了HMM的有效性。姜万录等[15]提出了结合支持向量聚类和连续HMM的轴承退化评估方法,说明HMM模型能有效地对轴承运行中的不同退化状态做出诊断和预测。但传统HMM中用于参数学习问题的Baum-Welch算法容易在训练过程陷入局部最优的情况。基于此,ZHENG等[16]将遗传算法用于HMM的参数优化,改进后的HMM对光伏逆变器故障的诊断速度更快、更准确,但遗传算法存在早熟、局部寻优能力差的问题。其次,HMM在实际应用中容易对数据进行过度拟合,通过采用变分贝叶斯(variational bayesian,VB)改进隐马尔可夫模型解决该问题。
综上所述,针对S变换和HMM模型存在的不足,本文提出一种基于广义S变换和变分贝叶斯-隐马尔可夫模型(VB-HMM)的滚动轴承性能评估方法。首先,利用广义S变换对滚动轴承振动信号进行特征指标提取;其次,结合变分贝叶斯改进后的隐马尔可夫模型评估滚动轴承性能退化过程;最后,利用轴承退化的实验数据验证所提出方法的可靠性和准确性。
1 基于广义S变换的滚动轴承特征指标提取
1.1 S变换
连续S变换可基于小波变换或者短时傅里叶变换引出,对于一维信号x(t),其连续S变换S(τ,f)可定义为:

(1)
式中:S(τ,f)为信号的S变换形式,f为频率,ω(t-τ,f)为高斯窗函数,τ为对应窗函数的时间中心,其中:
(2)
S变换具备可逆性,其反变换式定义为:
(3)
1.2 广义S变换
由于S变换时频分辨率受窗函数形式固定限制,无法灵活调节窗宽使其在实际应用中受到限制。因此引入调节系数k来对高斯窗进行改进,其表达式为:
(4)
改进后的广义S变换表达式为:

(5)
通过改变调节系数k可以改变时频分辨率,当k=1时,为标准S变换;当k>1时,此时时域分辨率与高斯窗的宽度成反比,窗宽越窄,在分析信号时时域分辨率更为优秀;当k∈(0,1)时,在处理信号时的频域分辨率与窗宽成正比。以灵活改变k的大小的方法来改善S变换使其更为广泛地运用于实际应用。
为了验证广义S变换的效果,进行仿真信号分析:
(6)
图1显示了原始信号和当k取不同值时仿真信号的时频谱。第2幅图为k=1时的普通S变换;第3幅图为k=0.4时,广义S变换的频域分辨率明显优于第1幅图;第4幅图为k=1.5时,此时高斯窗变窄,时域分辨率变高。
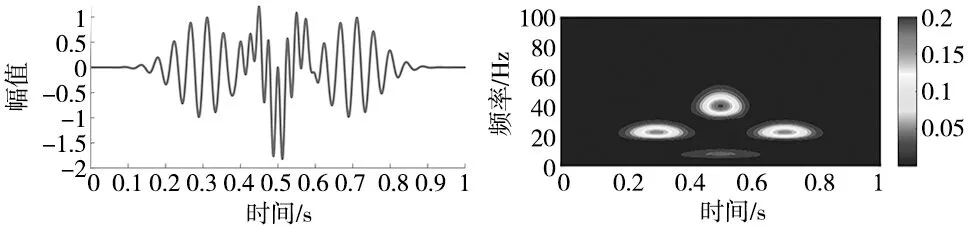

图1 仿真信号的时频谱
凭借快速傅里叶变换(FFT)使广义S变换离散化以达到快速处理计算机上实际信号的目的,得到广义S变换离散化公式,可表示为:
(7)
式中:N为x(t)的采样点数,T为x(t)的采样间隔,假设时间序列{X[kT],k=0,1,2,…,N-1}是x(t)的离散时间序列,对被分析的信号X[KT]进行广义S变换后得到的结果是一个复时频矩阵。该矩阵被取模以达到简化处理的目的,得到广义S变换的模矩阵,此时矩阵的行列实际意义分别为离散频率和采样时间。
1.3 广义S变换熵值指标
信息熵利用状态的概率分布来估算系统的复杂度和随机性[17]。假定若一个离散的随机变量X=[X1,X2,…,Xm]以概率为P=P(xi)(i=1,2,…,m)的情况发生,且满足:
(8)
则X的信息熵可表示为:
(9)
信息熵的熵值越大,表示该事件含有的信息量越少,发生的概率越低。
广义S变换是一种具有多分辨率特性的振动信号时频分析方法,信息熵可以衡量系统的复杂性,评价随机信号在总体上的不确定性。综上所述,将广义S变换和信息熵相结合,提出结合两者优势的GST-熵值指标作为评价滚动轴承的性能特征指标。
采用广义S变换提取性能特征指标的基本过程如下:
(1)对采样长度为N的时序信号X进行广义S变换,得到一个相应矩阵,进一步取模处理,获得一个N×N的时频谱系数矩阵,记为Y。
(2)对矩阵Y的行、列分别按照式(9)进行信息熵处理,将所得N个特征值取平均,分别得到GST-频率熵与GST-时间熵。
(3)对矩阵Y的时频谱矩阵整体按照式(9)进行信息熵处理,得到GST-时频熵。
2 基于隐马尔可夫的性能评估模型
2.1 隐马尔可夫原理
HMM由两个随机过程组成,其中一个随机过程序列中的状态是不可观测的,而是通过观测值序列来估计。另一个则可直接通过可观测量估计其隐藏的状态[18]。
HMM包括3个概率矩阵和2个状态集合,分别是隐含状态S,可观测状态Y,隐含状态转移矩阵A,观测状态转移概率矩阵B,模型初始时刻状态概率分布π。
在滚动轴承性能评估过程中进行轴承状态诊断时,无法通过观察直接得出其实际状态,而是通过轴承工作时产生可监测的的振动信号作为判断其状态的依据。该过程可以看作马尔可夫模型的双随机过程。
2.2 变分贝叶斯原理
变分贝叶斯(variational bayesian,VB)的产生是建立在传统贝叶斯推断与EM估计算法的基础上,同时结合导入了变分近似理论。
模型统计中,用Y表示观测数据样本,θ、Z分别表示未知模型参数以及潜变量,从而得到后验分布p(Z|Y)。在进行求解后验概率分布时,凭借一种简单分布q(Z)去代替后验分布p(Z|Y),以达到消除后验分布的复杂性对求解精确解的影响[19]。引入度量指标KL散度(kullback-leibler divergence)来描述q(Z)对p(Z|Y)的逼近程度。变分贝叶斯模型的对数似然函数可以等价表述为式(10):
(10)
定义L(q)和KL(q‖p)将式(10)的等价表达为式(13):
(11)
(12)
logp(Y)=L(q)+KL(q‖p)
(13)
式中:KL(q‖p)≥0,L(q)为变分自由能。当q(Z)与p(Z|Y)同分布时等号成立,此时KL散度达到最小值,即使变分自由能最大化,使q(Z)≈p(Z|Y),近似分布可认为等价于后验分布。
2.3 基于变分贝叶斯改进的隐马尔可夫模型
传统的隐马尔可夫模型与贝叶斯算法存在以下两个问题:
(1)隐马尔可夫模型拟合时的参数量可能大于可行的数据量,模型内存在着许多参数和观测数据。在进行参数求解时,多数时候无法避免模型复杂度导致容易对数据过度拟合的情况,这是由于传统的HMM通常选取极大似然估计的方法。
(2)贝叶斯算法无法在隐马尔可夫模型中直接运用,通常而言,信号分析的有效性受参数边缘化过程影响,由于该过程往往伴随着积分计算产生相应的运算量。
为解决上述问题,可以采用变分贝叶斯代替极大似然估计来估计参量从而改进隐马尔可夫模型。具体步骤为:
首先,式(14)和式(15)描述的似然函数分别对应隐马尔可夫模型中的隐含状态和观测数据。
(14)
(15)
参数可在基于贝叶斯推断的原理上将后验密度表达为式(16):
(16)
此时变分贝叶斯的应用是为了进一步处理式(16)中无法计算的分母,在该步骤中为了获取期望的估计q(θ,S)应当使下界L(q)取最大值,同时避免过拟合问题。边缘似然为:
(17)
通过对式(17)两边取对数后再取后验分布q(θ,S)的期望,得到:
logP(Y)=∬q(S,θ)logP(Y,S,θ)dSdθ=
-∬q(S,θ)logP(S,θ|Y)dSdθ
(18)
整理式(18),可得:

(19)
可将式(19)表达为式(11)~式(13)的形式。此时KL散度达到最小值,即下界L(q)最大,来实现logp(Y)的估计。
下界可表示为:
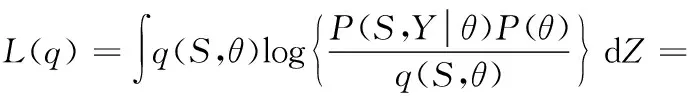
(20)
式中:S为状态,θ为参量。
变分贝叶斯改进的迭代过程中需要一个VBE步骤来推断隐含变量,以及一个VBM步骤用来推断模型参数的后验分布。通过对式(20)求偏导函数获取两个步骤中运算所需要迭代的方程。
(1)VBM-步骤。
(21)

(22)
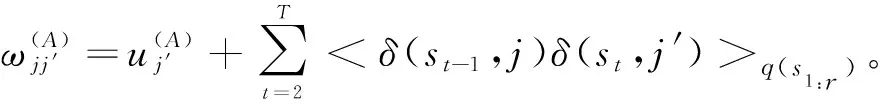
(23)

(2)VBE-步骤。
(24)
(25)
(26)

VB-HMM模型采用前向-后向算法,表达为:
(27)
(28)
若下界L(q)处于可以忽略不计其极其微小的变化时,此时满足了VBEM算法的终止条件。
2.4 基于VB-HMM模型的状态性能评估
首先选取正常状态下滚动轴承的数据作为训练样本,应用2.3节的变分贝叶斯-隐马尔可夫模型建立性能评估模型,得到轴承正常阶段的VB-HMM模型;然后将待测数据输入已训练好的VB-HMM模型,计算输出其偏离值,实现对滚动轴承的性能退化分析。
具体的滚动轴承性能评估流程如图2所示。
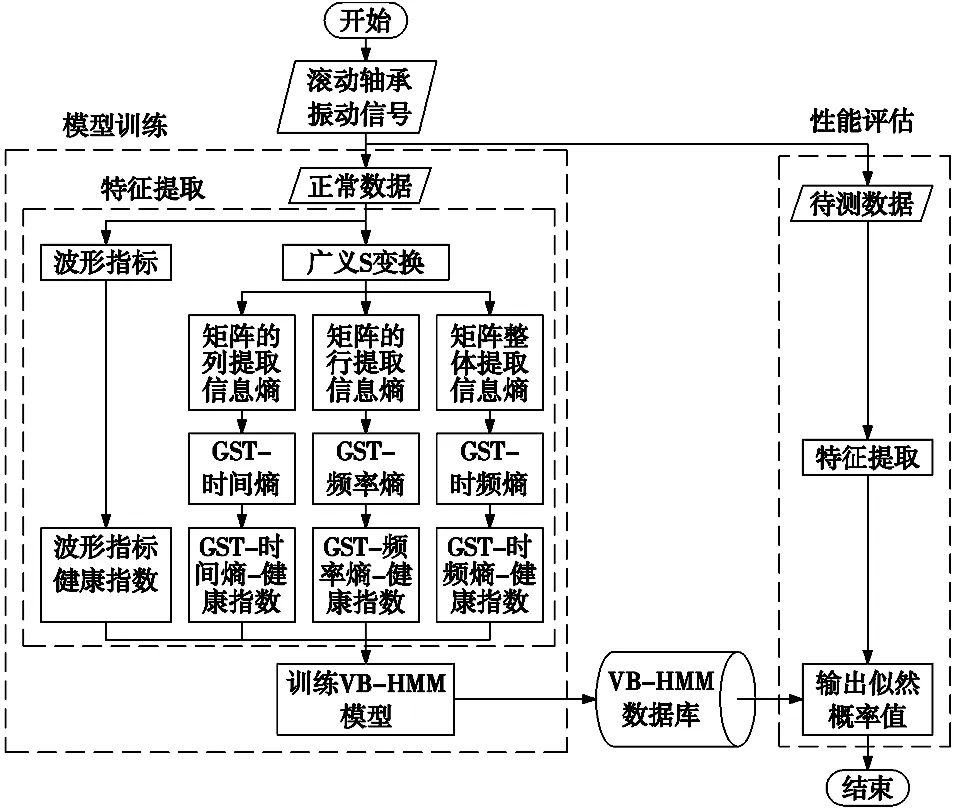
图2 基于VB-HMM的性能评估流程
步骤1:根据图2的特征指标提取流程,提取出正常状态下的滚动轴承特征向量,训练得到正常状态的VB-HMM模型;
步骤2:对待测数据同样经历步骤1的特征提取,得到样本将其输入到训练好的模型中;
步骤3:通过模型计算输出测试样本的对数似然概率值,达到性能评估的目的。
3 广义S变换的实验与结果分析
3.1 模拟信号仿真实验
根据故障位置的不同,滚动轴承的点蚀故障可以分为滚动体故障、内圈故障和外圈故障。因此,假定滚动轴承承受不同冲击强度A时故障数学模型可以表示为:
(29)
式中:Ai为调制幅值,τi为微小滑动,n(t)为高斯噪声,fn为系统共振频率,B为系统共振衰减系数。
根据美国辛辛那提大学(IMS)提供的轴承全寿命疲惫实验数据进行实验。该实验装置中含有4个施加了2700 kg径向载荷的轴承,转速保持在2000 r/min,轴承节圆直径为7.15 cm,一个周期的数据长度为2048,滚动体的直径为0.84 cm[20]。总共含有3组轴承的全寿命实验数据,本文使用数据集2的数据,采样频率为20 480 Hz,轴承振动信号采样间隔为10 min/次,共采集到984组样本。冲击强度取值为A0={1,5,10},根据故障类型参考表1分别取值冲击幅值调制频率fm和冲击周期T。

表1 fm和T不同故障取值
当滚动轴承处于内圈故障、外圈故障和滚动体故障时,对一个周期内的仿真信号分别提取GST-时间熵、GST-频率熵、GST-时频熵特征指标。结果如图3~图5所示。处于3种不同的故障类型时,随着冲击强度加大,滚动轴承的故障程度逐渐加深,GST-时间熵、GST-频率熵、GST-时频熵-均逐渐减小。该变化验证了GST熵值特征指标的有效性。
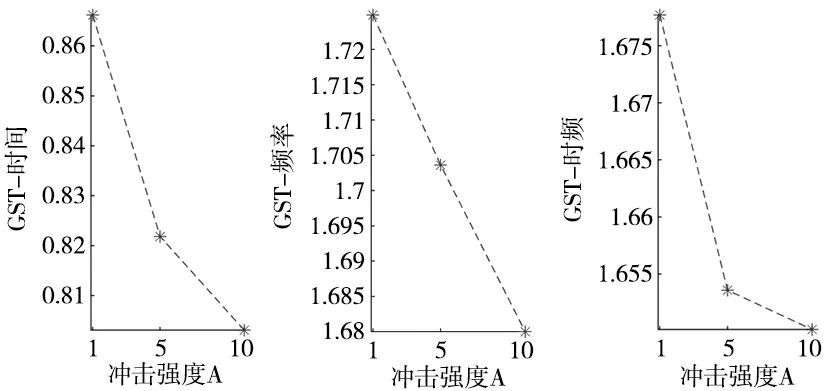
图3 内圈故障时不同GST熵值指标

图4 外圈故障时不同GST熵值指标

图5 滚动体故障时不同GST熵值指标
3.2 GST熵值指标实验与结果分析
为了进一步验证GST-时间熵、GST-频率熵、GST-时频熵3个特征指标在滚动轴承实际性能退化过程中的可行性,采用IMS提供的轴承全寿命疲惫实验数据进行实验验证。波形指标是应用较为广泛成熟的时域指标,表达式为:
(30)
同时将GST熵值指标与波形指标在滚动轴承全寿命周期中的变化情况进行对比。
图6为辛辛那提轴承振动信号的时域波形和经过广义S变换后的时频谱图。
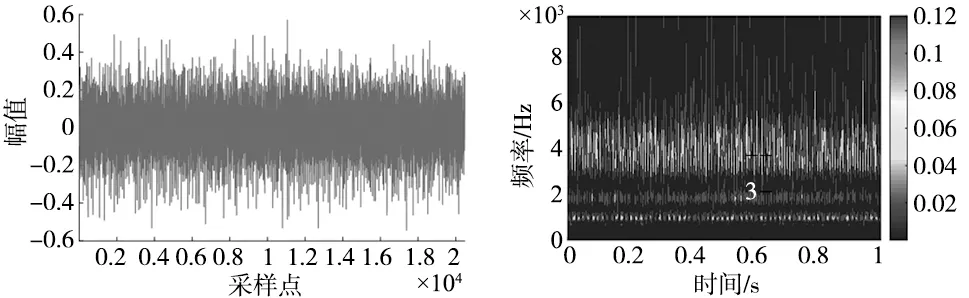
(a) 时域波形 (b) 二维时频谱图

(c) 三维时频谱图图6 辛辛那提轴承振动信号GST时频谱
图6b和图6c分别是轴承信号经过广义S变换后的二维时频谱和三维时频谱。图6c中X轴为时间轴,Y轴为频率轴,Z轴表示幅度。图6c显示了轴承振动信号经广义S变换后能量随频率和时间的变化,具有较高的时频分辨率。
图7分别是波形指标、GST时频熵、GST时间熵和GST频率熵在全寿命周期里随时间变化的曲线。曲线变化过程共分为4个阶段。第1阶段曲线基本处于平稳状态,该阶段滚珠轴承处于正常工作的健康状态。第2阶段曲线开始上升或者下降,该阶段滚动轴承处于早期微弱故障阶段。第3阶段曲线产生震荡,但震荡幅度较小,该阶段滚动轴承故障程度随着时间加剧。第4阶段曲线开始剧烈震荡,震荡频率较上一阶段明显增大,直到最后上升或者下降至新的极点,该阶段滚动轴承经过不断磨损逐渐失效。整个曲线展示了滚动轴承从健康状态到故障逐步加深直至失效的过程,曲线变化与滚动轴承实际变化较为一致,验证了GST熵值指标的有效性。

图7 辛辛那提全寿命周期不同特征指标曲线
表2为不同特征指标在滚动轴承不同阶段的对比表,结合图7分析可得以下结论:

表2 不同特征指标对比表
(1)波形指标相对于GST熵值指标,对于滚动轴承从早期故障到严重故障直至失效阶段的变化并不明显。
(2)GST-时间熵相对其他3种特征指标对滚动轴承早期微弱故障最为敏感,反应时间早,有助于初期的维护运行。
(3)GST-频率熵对早期故障灵敏度相比于GST-时频、GST-时间熵较低,但严重故障到失效阶段反应时间有所提前,有助于在滚动轴承严重故障时及时检测停机维修。
3.3 健康指数
为了更好的描述滚动轴承的性能退化失效过程,便于划分失效状态,方便后续数据处理更加便捷快速,通过式(31)对GST-熵值指标进行归一化处理,获取相应的健康指数(health index,HI)指标,将取值范围映射到[0,1]之间。
(31)
经过处理后的健康指数曲线波动范围在0~1之间,初期健康指数曲线较为平稳且数值较小,随着滚动轴承不断磨损故障加深,曲线开始上升并在达到一定之后开始波动。
为了进一步应用于实际应用中,将滚动轴承的健康状态划分为4个状态。在健康指数曲线处于较为稳定阶段,实时健康等级评估为健康;曲线开始上升时,滚动轴承出现损耗进入早期微弱故障,实施健康等级评估为亚健康;当曲线出现波动后跌至新的最低点,此时滚动轴承性能严重退化,根据曲线震荡幅度的大小可分为监控运行与建议停机2个阶段。
4 VB-HMM实验与结果分析
4.1 VB-HMM健康评估与分析
为了进一步描述滚动轴承性能退化过程,采用上文所说的变分贝叶斯-隐马尔可夫状态评估模型,选取上述数据集2中采集到的984组数据样本进行实验,根据图2的VB-HMM性能评估流程,分别提取GST-时间熵健康指数、GST-频率熵健康指数、GST-时频熵健康指数和波形指标健康指数4个特征指标作为VB-HMM模型的输入。将正常状态下100组轴承数据用来训练模型,整体数据为测试数据。
为了进一步验证VB-HMM评估模型在性能退化中准确性,分别使用采用传统HMM和VB-HMM两种模型进行性能评估。
全寿命周期的HMM变换曲线如图8a所示,在滚动轴承运行的1~696组期间,样本的曲线处于平稳状态,说明其运行属于正常状态;在697~755组阶段,曲线呈缓慢下降趋势,但幅度较小,对数似然概率值逐渐减小,此时滚动轴承开始出现轻微磨损,性能开始劣化并保持该状态继续运行;在随后的756~984组中,曲线开始处于较大幅度的波动,并在最后跌至最低点,说明该期间的滚动轴承磨损严重,出现较大故障,性能退化至失效。
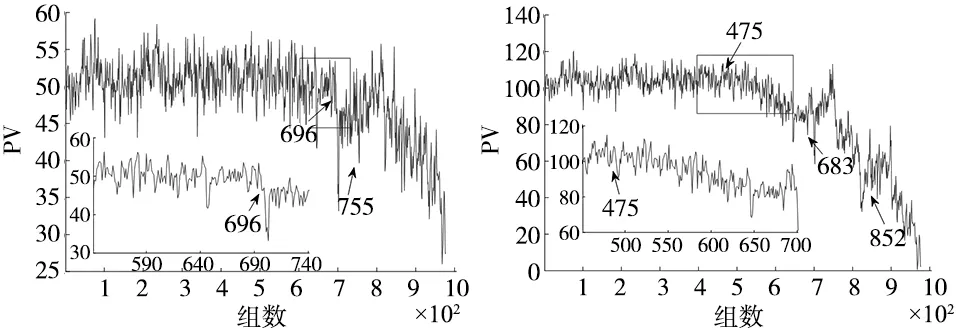
(a) HMM (b) VB-HMM图8 全寿命周期似然对数曲线
图8b中,在1~475组阶段中滚动轴承处于正常运行阶段,曲线保持平稳。在第476组样本处出现了早期故障,曲线逐渐下降偏离正常状态。退化曲线在684~852组过程中产生波动震荡,此时滚动轴承开始故障恶化;从853组直至曲线结束,滚动轴承深度劣化直至损坏,过大的冲击使曲线震荡较上一阶段更为频繁,到最后完全失效对数似然概率值达到最小值。
基于两种方法的对比结果如表3所示,结合图8分析,HMM模型的对数似然概率值相差35个单位,VB-HMM的取值区间为120个单位,所以VB-HMM的变化趋势更加清晰明显。HMM模型在第696组样本处开始出现早期故障,但曲线下降程度微弱,VB-HMM模型在第476组样本处开始出现早期故障,说明VB-HMM模型在滚动轴承早期微弱故障阶段更为敏感;同时,VB-HMM模型在第684本样本后可分为两个阶段,684~852组为磨损程度逐渐加深的阶段,853~984组为失效阶段,而HMM模型在756~984组过程中曲线震荡幅相差不大。由此可以看出:在滚动轴承从健康到劣化失效整个期间,VB-HMM模型比HMM模型更为清晰有效的表征退化过程。

表3 HMM和VB-HMM结果对比
且结合3.3节的健康指数分类实时评估,可得滚动轴承在1~475组阶段为正常工作状态,处于健康状态的时间为4760 min;476~683组滚动轴承为早期故障,处于亚健康状态时间为2070 min;684组~852组滚动轴承故障加剧,处于监控运行阶段时间为1690 min;从853组直至结束,滚动轴承严重劣化已影响正常工作,处于建议停机的时间为1320 min。滚动轴承从监控运行转为建议停机状态的转折时刻可作为最佳预警的时间点,即平均提前50.1 h启动预警。
本文VB-HMM模型对辛辛那提大学滚动轴承数据性能评估结果,与文献[21]中:判断1~539组为正常运行状态,处于540~699组时,滚动轴承为缓慢损坏阶段,在700~984组阶段,滚动轴承处于严重损坏直到失效阶段。两者在判断正常运行状态以及早期故障和故障加剧阶段结论基本一致,但本文在判断早期故障阶段更为灵敏;并进一步区分了故障加剧和严重故障至失效阶段,在实际检测维修应用方面更为灵活。这验证了本文变分贝叶斯-隐马尔可夫模型的可行性。
4.2 评估结果验证
计算ZA-2115轴承各部件的故障特征频率,如表4所示。

表4 ZA-2115轴承故障特征频率
为了验证4.1节评估结果的正确性,对健康等级变换节点前后进行包络谱分析,分别为第420组样本、第476组样本、第684组样本和第853样本,分析图如图9所示。

(a) 第420组 (b) 第476组
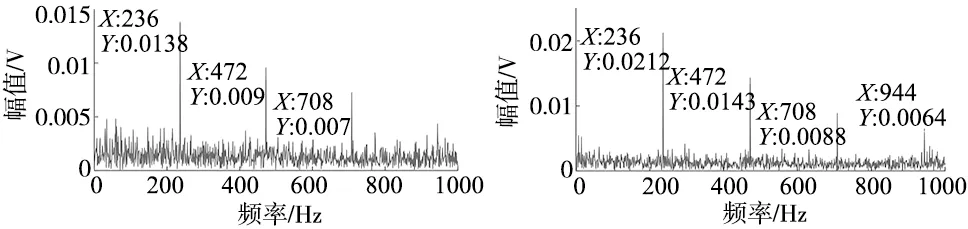
(c) 第684组 (d) 第853组图9 健康等级变换节点数据包络谱分析图
由图9可知,图9a中,第420组数据样本无故障特征频率,滚动轴承为正常工作状态;图9b中,第476组数据样本包络谱图出现了236 Hz,与表4中外圈故障的频率接近,可判断该滚动轴承的故障类型是外圈故障,且滚动轴承处于早期故障阶段;图9c中,第684组数据样本频率幅值增大,且外圈故障1倍频、2倍频和3倍频特征明显,说明滚动轴承进一步劣化,为监控运行阶段;图9d中,第853组数据样本出现外圈故障1倍频、2倍频、3倍频和4倍频,此时故障严重直至失效,建议停机。
各个变化节点的包络谱变化与4.1节VB-HMM模型实时评估结果是一致的,证明了该模型的有效性。
5 结束语
结合广义S变换与信息熵对滚动轴承进行性能退化特征指标提取,并计算相应健康指数,通过滚动轴承模拟信号仿真实验证明了广义S变换熵值指标的可行性;并通过辛辛那提大学的滚动轴承全寿命实验数据进一步说明了广义S变换熵值指标在整个性能退化过程的变化趋势,该变化趋势与滚动轴承从健康状态到损坏状态的动态变化趋势相符合,验证了其有效性。
最后,结合变分贝叶斯改进后的隐马尔可夫模型,建立了滚动轴承的状态评估模型,采用标准实验数据对模型的有效性进行了验证,其曲线变化良好的描述了轴承从正常运行到早期故障直至损坏的退化过程,对滚动轴承实时监控和运行评估具有一定的实际应用价值。
