面向手眼系统的摄像机内参数自标定研究*

2023-08-02朱世雄葛动元姚锡凡向文江

组合机床与自动化加工技术 2023年7期

朱世雄,葛动元,姚锡凡,向文江,李健

(1.广西科技大学机械与汽车工程学院,柳州 545006;2.华南理工大学机械与汽车工程学院,广州 510640;3.邵阳学院机械与能源工程学院,邵阳 422004)

0 引言

工业机械臂搭载视觉传感器已成为当前工业机器人的主流趋势,因此视觉系统越来越受到工业机器臂领域研究的广泛重视[1]。而摄像机标定作为手眼系统的前置基础,其意义是由摄像机几何模型参数的数学变换确定二维图像坐标系与三维空间机械臂坐标系的转换关系。传统的标定方法是用已知尺寸的参照物(如标定板,标定块等),建立参照物上坐标点与图像中的对应点来计算摄像机的内参数,如TSAI[2]提出的两步标定法就是这类方法的典型代表。然而这种方法需要对初值的进行选定,且值对后续标定精度影响较。MAYBANK等[3]提出摄像机自标定的思想。这种方法无需特定参照物,灵活性强,可实现在线标定,继之很多研究人员提出了一些其它的类似方法[4-7],但这些自标定方法大多需要图像中包含特定的立体信息,并且鲁棒性差,精度不高。为解决这一问题,吴福朝等[8]利用多组平面正交平移运动,基于图像的单应性矩阵建立线性方程组,从而完成包含倾斜因子在内的五参数摄像机标定。刘雨琪等[9]对基于单应性矩阵的方法进行改进,构建了镜头间的约束关系,实现了多镜头相机的参数标定。吴文欢等[10]通过不同平面运动产生的不同单应变换,计算得出单应性矩阵的复特征向量,进而线性求解相机内参数。相对于像点到物点的单向映射的几何模型,还有学者使用了另一种隐式标定-应用神经网络。葛动元等[11]通过摄像机物理模型设计一个新型正交权值的神经网络,同时引进混合遗传模拟退火算法,在系统达到全局最优解平衡状态时,得到摄像机的内外参数。GE等[12]还引入了消失点的正交性,根据其约束关系设计正交学习神经网络进行摄像机标定。本文是基于前者主动视觉的自标定,讨论了一种面向手眼系统中摄像机的自标定方法,在经过一次极点延伸运动与一组三正交平移运动后,可通过基于图像单应性矩阵线性约束方程组得到摄像机内参数。此方法只需两组平移运动,简化了实验步骤,且具有较好的标定精度,很容易在手眼系统中实现。

1 摄像机模型

文中的摄像机模型都假设为经典的针孔模型,为了后续摄像机内参数求解方便,可将内参数矩阵A表示为:

1.1 摄像机主点的确认

假设摄像机在空间中经过平移运动后,前后摄像机的对应光心分别为Oc1、Oc2,两摄像机坐标系之间变换关系为Xc2=RXc1+t,所拍摄的两幅图像的对应点之间存在固有射影性质-极几何约束。三维空间点M、N在两相机投影成像平面上的投影分别为m,n,与m′,n′点。若世界坐标系与摄像机光心为Oc1的摄像机坐标系重合。则有R=I,t=0,空间点M投影到第一个摄像机坐标系的关系为:

s1m=AM

(1)

第二个摄像机相对于第一个摄像机的方位为[Rt],在保持摄像机前后内参数保持不变的情况下,空间坐标点M在第二幅图像上的投影为:

s2m′=A(RM+t)

(2)

式中:s1、s2均为非零常数因子。

可得到e′是第二幅图像的极点,即第一个摄像机坐标系原点即光心在第二幅图像上的投影,将光心代入可得:

(3)

同理可得,第二个摄像机坐标系光心在第一幅图像上的投影代入并进行整理可得:

(4)

两幅图像对应点之间的极几何约束,可用秩为2的3阶基本矩阵F来表示,基本矩阵是两幅图像间的固有射影性质。其有如下性质[13]:

m′TFm=0

(5)

极点延伸运动是指摄像机垂直于物方面(标定板)的平移运动。本实验中,摄像机在进行平移运动时,其所有对应点的连线轨迹所形成的直线都相交于极点,如图1所示,当运动为极点延伸运动时,极点e与图像像素坐标系原点O1重合,即极点为图像平面的主点。

图1 极点延伸运动示意图

由于是在纯平移运动下,旋转矩阵R为单位矩阵,即e=e′≈At,则基本矩阵F通过代数运算表示为:

F=A-T[t]×RA-1=A-TRAT[ARTt]×=
A-TRAT[e]×=[e]×

(6)

式中:[t]×,[e]×为向量t=(ta,tb,tc)T与e=(a,b,c)T对应的反对称矩阵,即:

(7)

当向量e成为反对称矩阵时,极点可根据式(8)由两个或者两个以上的图像对应点求得:

(8)

如图1所示,利用两幅图像的几何表示来刻画基本矩阵F,根据马颂德[14]提出的定理:根据m′,n′点在第二幅图像坐标系中的坐标值,将其在第一个图像坐标系中的位置用m′′,n′′表示,本研究称m′′与m为同一图像中的对应点,在纯平移运动下,m′′,m与n′′,n的连线交于同一点e(极点),带入式(5)可得直线方程:

(v-v′)a+(u′-u)b+uv′-u′v=0

(9)

式中:(u,v,1)T、(u′,v′,1)T为上述对应点,极点e=e′=(a,b,1)T。

由式(9)构建关于直线的线性方程组,在摄像机进行极点延伸运动时,其多个对应点连线所拟合的最小二乘解就是所求主点。

1.2 单应矩阵

以摄像机坐标系光心Oc1为端点向平面C作射线可交平面于M点,所拍摄世界平面C的方程为:nTM=d,其中单位法向量为n,d为坐标系原点到平面的距离,如图2所示。

图2 由平面C诱导的单应变换H

对于空间中的点M,其齐次坐标[M,w]与第一个图像坐标系之间通过经典的针孔模型相关联:

(10)

根据空间点M在图像平面的投影像点位m,则射线[(s1A-1m)T,w]T上所有的点都投影在m这个像点,如图2所示。将射线代入平面C方程中,可求得该射线与平面的交点:

M=s1[(A-1m)T,-nTA-1md-1]T

(11)

对于空间点M在OC2第二幅图像坐标系上得投影可得:

(12)

式(12)可整理为m′=sHm,其中s=s1/s2,即在相差一个非零常数因子意义下相等m′=Hm,Oc2表示摄像机光心在世界坐标系上的非齐次坐标。

因此两幅图像之间的单应矩阵可表示为:

H=σA(R+d-1tnT)A-1

(13)

1.3 求解单应矩阵

两幅图像对应点之间的映射可确定一个3×3的可逆矩阵H:

m′=Hm

(14)

式中:H=[h1h2h3],hi=[hi1hi1hi1]T(i=1,2,3),将齐次坐标进行展开可得:

(15)

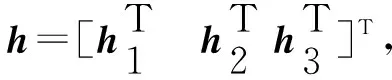
(16)

这些方程组合起来得到:

Nh=0

式中:N为2i×9的矩阵。

图像上一对对应点可以提供两个线性方程,在相差一个常数因子的意义下,给定4对以上(i≥4)的图像匹配点便可以估计出单应矩阵H。

1.4 确定常数因子σ

单应矩阵根据式(13)变换可表示为:

H-σI=Ad-1tnTA-1

(17)

由于上式右边等式秩为零,可知det(H-σI)=0,对于所有的2阶子矩阵有:

det(H-σI)2×2=0

(18)

由此可建立6个关于常数因子σ的一阶方程,最终在实际计算中σ视为线性方程组的最小二乘解。

2 五参数模型的摄像机自标定

在本步求解中,摄像机在平移前后各拍一幅图像,利用图像单应性矩阵构建线性约束方程组。在纯平移运动下,给定一组三正交平移运动其平移向量组T={t1,t2,t3},其中t1,t2,t3是两两正交的平移向量。

(19)

(20)

将式(20)方程组中方程两边取转置,并右乘式(19),则有:

(21)

由式(21)可得:

(22)

由此构建线性约束方程组:

(23)

摄像机内参数中主点u0,v0已知,只需得到u轴与v轴的等效焦距fu,fv和倾斜因子λ,可对内参数矩阵进行拆分,令:

(24)

(25)

(26)

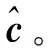
综上所述,本文的线性摄像机自标定算法总结为:

输入:一组极点延伸运动与一组三正交运动得到的图像。

输出:摄像机5个参数fu,fv,u0,v0,λ。

步骤1:对平移运动过后得到的图像进行特征点坐标提取,并根据极点延伸运动所得图像确定主点;

步骤2:计算三正交运动下,两两正交平面的单应矩阵Hi(i=1,2,3);

步骤3:求解对应的常数因子σi(i=1,2,3);

步骤4:利用所求得的不同平面约束建立线性约束方程组:

②确定摄像机内参数:

③最后再将主点代入得到最后的摄像机内参数A。

3 实验与分析

在实际实验时,特征点的提取不可避免的有着噪声影响,为了检验该算法的鲁棒性,在不同噪声水平下进行模拟实验。具体选取摄像机的理论值为:图像大小(像素数):640×480;图像点个数20;摄像机内参数的理论值为u0=320,v0=240,fu=fv=1000,λ=0.2。噪声水平作如下定义,假设一个理想点坐标为(u,v),那么在噪声水平N的影响下,实际坐标变为:(uN,vN)=(u,v)+(N*rand1,N*rand2)。摄像机作一组三正交运动,每次平移前后采集2幅图像,选取第1张为起始图像,后续3张是摄像机运动后所得。对图像数据加入不同水平的随机噪声(单位:像素)。在每一个噪声水平下运行100次,计算所求出的内参数的均值和均方误差。表1是各噪声水平下所求内参数均值的统计表,图3是所求得的摄像机内参数在不同噪声水平下的均方误差变化趋势。

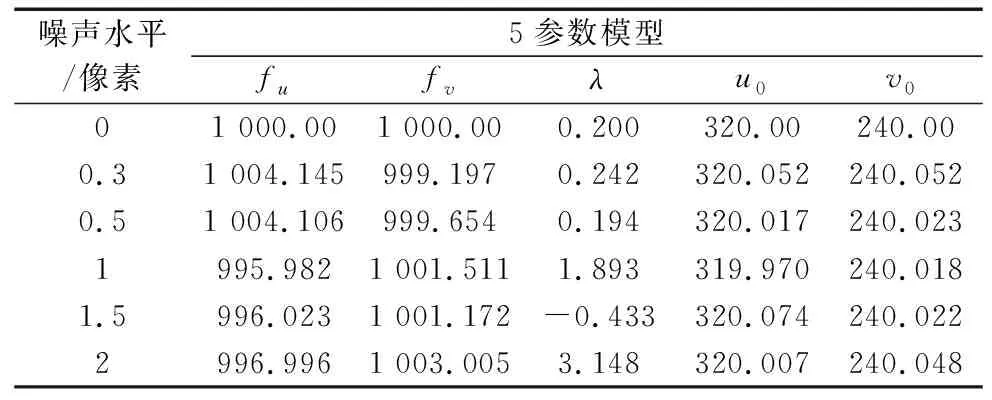
表1 不同噪声水平下摄像机内参数标定结果的均值统计表

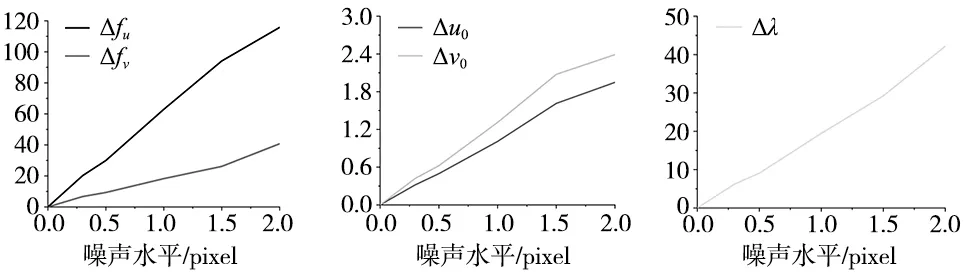
(a) 等效焦距 (b) 主点 (c) 倾斜因子图3 不同噪声水平下的摄像机内参数标定结果的均方误差变化曲线

由表1的仿真结果可看出,在有相当水平的噪声情况下,本文的摄像机线性标定方法仍含有较好的标定结果,同时根据图3a～图3c的变化曲线可看出摄像机内参数均方误差随噪声水平的不断增大呈线性增加趋势。在2个像素噪声水平内,fu的均方误差小于11.5%,与之对比fv受噪声干扰非常小,均方误差小于4.07%,u0和v0的均方误差均小于1.12%,可看出内参数的均方误差在可接受范围内,以上均说明本文提出的自标定方法精度比较高,鲁棒性也比较强。

3.1 真实图像实验

在真实图像实验中,使用ABB工业机器人IRB2600来进行标定实验,如图4所示,在机械臂末端安装视觉系统,利用机械臂的运动来控制摄像机的位姿变化,获取多个不同视角下的标定板,从而进行摄像机标定。摄像机分辨率大小为640×480,标定板采用7×7 mm的棋盘标定板,每幅模板图像含有8×11个标定点。首先控制机械臂进行极点延伸运动,对运动前后两图像进行棋盘角点的点集获取,如图5a所示。将两个对应点作为一组进行直线拟合,如图5b所示。将坐标代入式(9),由于数据和数值计算误差等原因,在实际计算中主点视为多对对应点所构建线性方程的最小二乘解,计算得主点坐标(u0,v0)为(358.873,139.836)。

图4 手眼系统

在进行三正交运动时,本文依次取的点是A(15,-5,-5),B(15,5,-15),C(15,0,-20)三个点位运动,获取包括初始图像在内的4幅图像,两两正交的平移向量组T={t1,t2,t3}。其形成的单位向量为t1=[0.0105,-0.0315,0.0315]T,t2=[0,0.05,-0.05]T,t3=[0.0315,-0.0052,0.0052]T。然后利用摄像机采集的齐次坐标点根据式(16)计算单应矩阵:

经过矩阵求逆后得到:

表2 方法所得摄像机内参数

3.2 重建验证所得内参数

为了检验标定结果的准确性,利用文献[15]的开源算法对表3中物体进行重建以验证所得到的摄像机内参数。在摄像机内参数未改变的情况下拍摄的多张零件图像,包括长度为75 mm的螺栓,长度为115 mm的直柄麻花钻和齿顶圆直径长度为90 mm的直齿轮,图6所示为直齿轮三维重建流程。表3为处理后的输出效果图。

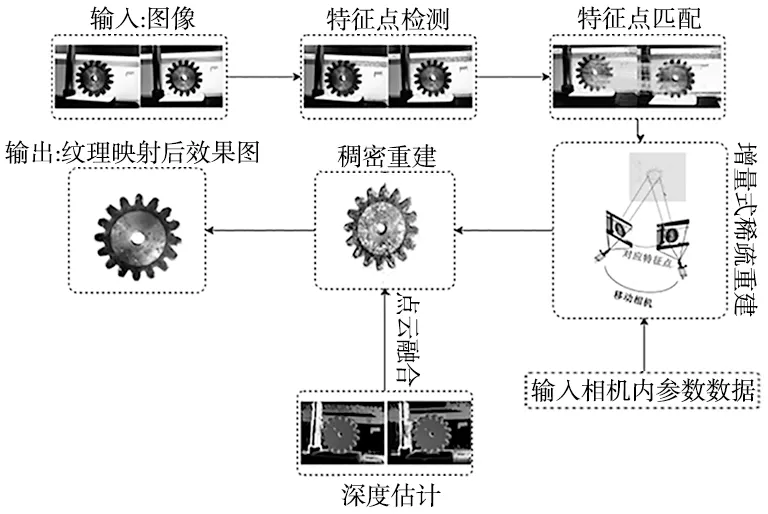
图6 三维重建流程图

表3 不同零件的重建结果

根据立体视觉的物理意义,双目视觉系统在三维重建中具有较高的精度[16]。以双目深度传感相机ZED 2i在相同视角范围内进行三维重建(摄像机参数已知),将ZED 2i生成的三维点云模型看作参考值,与上述手眼系统中的摄像机构建的三维点云模型(待比较值)进行对比分析,通过计算两者三维模型之间的绝对距离大小来验证摄像机内参数。将参考值与待比较值的三维点云模型经过配准后进行比较,如图7所示,通过对点云的渐变着色来对应模型之间的距离大小,依据距离与点的数量关系给出直方图并对数据进行了高斯分布拟合。

(a) 螺栓点云模型对比结果 (b) 直柄麻花钻点云模型对比结果

根据高斯拟合得出螺栓的参考值与待比较值模型之间的平均距离为0.42 mm,标准差为0.55 mm。直柄麻花钻的参考值与待比较值模型之间的平均距离为0.81 mm,标准差为1.19 mm。直齿轮参考值与待比较值模型之间的平均距离为0.61 mm,标准差为0.90 mm,可以看出模型之间的绝对距离误差很小,多数点云距离误差都集中在1 mm之内,随着距离增加成指数型减少趋势。各零件拟合的高斯分布曲线峰值低于分布直方图峰值,且分布直方图呈中央聚拢型,说明实际的效果会更好。

为进一步进行精度评估,以零件长度的0.5%,1%,1.5%作为分界值,统计零件分界值内的点云数量与所占比例,统计结果如表4所示。