授权模式下考虑再制造设计的闭环供应链决策研究

魏杰 李志豪

摘 要： 基于一个原始设备制造商（OEM）和一个第三方再制造商（TPR）组成的闭环供应链，在授权模式下考虑OEM的再制造设计，构建了两周期动态博弈模型，分别给出了再制造受回收数量限制和不受回收数量限制下OEM的最优再制造设计策略及TPR开展再制造业务的边界条件，分析了再制造设计对供应链成员的利润影响。研究表明：当再制造不受回收数量限制时，OEM的最优再制造设计策略依赖于再制造设计为两种产品带来的收益之比和再制造成本节约度。此外，当再制造成本节约大于某一阈值时，TPR才会开展再制造业务。当再制造受回收数量限制时，OEM的最优策略是实施再制造设计、TPR总是应该开展再制造业务。无论再制造是否受回收数量限制，适当的再制造设计努力程度可以增加OEM的利润，再制造设计并不总是有利于增加TPR的利润。研究结果为OEM实施再制造设计和TPR进入市场提供了理论依据。

关键词：闭环供应链;授权模式;再制造设计;动态博弈

中图分类号： F274              文献标志码：A  文章编号：1674-7356（2023）-02-0012-12

引言

近些年来，随着资源枯竭问题日益严峻以及“双碳计划”的实施，企业通过回收废旧产品的剩余价值进行再制造，已经成为一种能够实现全面可持续发展的生产战略[1]。政府部门也高度重视再制造活动，2021年国务院在《关于加快建立健全低碳循环发展经济体系的指导意见》中明确提出，鼓励企业开展绿色设计、打造绿色制造工艺。产品的绿色设计（即再制造设计）在再制造中发挥着重要作用，它提高了产品的再制造水平，降低了产品的再制造成本[2]。例如：施乐利用一个便于再制造的拆卸设计，使复印机的再制造成本显著降低[3];博世通过开发一种低价的芯片，提高了废旧产品的质量，降低了家用电器的再制造成本[4]。然而，较高的再制造水平也降低了第三方再制造商（TPR）的生产成本，这使得原始设备制造商（OEM）在决策再制造设计时经常面临战略困境。

现实中，TPR从事再制造活动时，会用到OEM的产品专利，容易引发专利侵权问题，很多企业通过专利授權模式来避免相关的经济纠纷。例如：英国墨盒再制造商DCI在获得柯达授权后，再制造柯达品牌的墨粉盒;剑桥企业授权Aurelius Environmental再制造铅酸电池;苹果公司授权富士康再制造iPhone[5]。专利授权模式增加了OEM的额外收益，可弥补OEM的再制造设计成本。因此，在专利授权模式下OEM如何开展再制造设计是一个值得探讨的问题。

综上，本文在授权模式下考虑OEM的再制造设计，建立了两周期动态博弈模型，得到了再制造受回收数量限制和不受回收数量限制两种情况下OEM和TPR的均衡决策，通过定性分析和定量分析对新产品和再制造产品的均衡价格以及供应链成员的均衡利润进行了比较。主要回答以下问题：（1）在授权模式下，OEM的最优再制造设计策略及TPR进入市场的边界条件是什么？（2）当OEM实施再制造设计时，OEM选择生产高可再制造性产品的条件是什么？（3）再制造设计如何影响OEM和TPR的定价决策和利润？

一、文献综述

与本文相关的第一类文献是关于授权再制造的研究。一些学者研究了固定专利许可模式和单位专利许可模式的选择问题。易余胤和阳小栋[6]针对单个OEM和TPR组成的闭环供应链，发现当固定专利许可费用小于某一阈值时，OEM会选择单位专利许可模式。Qiao和Su[7]、Hong等[8]将模型拓展为两周期，也给出了OEM选择两种模式的临界值。Zhao等[9]将许可模式选择的研究扩展到经销商决策零售价格、第三方负责回收的情形。少数学者在固定专利许可模式下研究了再制造闭环供应链的相关问题。赵晓敏和孟潇潇[10]构建了含有单个OEM和TPR演化博弈模型，发现不同的固定许可费用条件会使系统演化至不同的均衡策略。赵晓敏等[11]143设计了可实现再制造闭环供应链协调的固定许可费用合同，达到了“OEM实施绿色创新、TPR实施再制造”的效果。也有些学者在单位专利许可模式下研究了再制造闭环供应链的决策与协调问题。Huang和Wang[12]、李巍等[13]通过考虑策略消费者和绿色消费者，在单位专利许可模式下研究了再制造闭环供应链的定价和生产决策问题。郑本荣等[14]在单位专利许可模式下研究了双渠道闭环供应链的定价决策。在此基础上，唐飞和许茂增[15]通过考虑消费者对两种渠道的不同偏好，给出了实现双渠道闭环供应链协调的收益分享机制。申成然等[16]和Zhang等[17]在单位专利许可模式下分别考虑了政府补贴和政府规制，研究了再制造闭环供应链的回收决策，发现政府介入可以有效提高企业从事回收再制造的积极性。然而，上述研究均没有考虑产品的再制造设计。实践中，为了实现可持续发展，OEM会在产品设计之初确定产品的再制造水平，即再制造设计。另外，相较于固定专利许可模式，单位专利许可模式对产品定价的影响更大。因此，本文基于OEM选择单位专利许可模式，通过考虑OEM在生产新产品的再制造设计努力决策，研究了OEM的再制造设计决策对产品定价和供应链成员利润的影响。研究表明，随着再制造设计努力程度增加，OEM将向TPR收取更多专利许可费。此外，再制造设计并不总是对供应链成员有利，当收益比值小于某一阈值时，TPR并不希望OEM实施再制造设计。

与本文相关的第二类文献是关于再制造设计的研究。一方面，在单周期环境下，夏西强和朱庆华[18-20]在不同的再制造模式下考虑了OEM和TPR分别承担再制造设计费用，得到了OEM实施再制造设计的边界条件。Liu等[21]考虑了供应商和OEM分别决策核心部件和最终产品的再制造设计，发现再制造设计可以抑制供应链成员的利润损失。另一方面，在两周期环境下，Wu[22]将产品设计分为易于再制造和不易于再制造两种情况，发现OEM可以通过改变产品设计策略来降低TPR的竞争力。Wu[23]考虑了TPR的高价策略和低价策略，认为OEM可以通过制定不同的产品设计策略迫使TPR选择不同的价格策略。曹晓刚等[24]考虑了产品的可拆卸设计，探讨了OEM的拆卸决策对产品价格和产量的影响。肖露等[25]1238考虑了政府生产税，认为政府可以通过改变生产税来激励OEM生产可再制造性高的产品。上述基于两周期环境下再制造设计的研究均认为TPR的生产经营不受OEM的制约，即独立再制造模式。鉴于专利授权对解决OEM和TPR之间利益冲突的重要作用，本文考虑TPR的生产经营需要获得OEM的授权（即授权再制造模式）且TPR的生产会受到旧产品回收数量约束的情形。研究表明，当再制造不受回收数量限制时，OEM是否实施再制造设计取决于收益比值和再制造成本节约的大小;只有当再制造设计为再制造产品带来的收益大于某一阈值时，TPR才会选择进入市场。当再制造受回收数量限制时，OEM会主动开展再制造设计，TPR会积极进入市场。

二、问题描述及基本假设

（一）问题描述

本文考虑一个OEM和一个TPR组成的两周期闭环供应链，如图1所示。其中，OEM在两周期内均销售新产品，TPR在第一周期末回收旧产品并在第二周期与OEM展开销售竞争。具体来说：在第一周期，OEM首先决定再制造设计努力程度，并投入相应的再制造设计固定成本kτ2/2;OEM然后以c-δnτ的单位可变成本生产新产品;OEM最后以p1的零售价格将新产品销售给顾客。在第二周期，TPR首先需要向OEM支付单位再制造产品的专利费用f;TPR然后将回收的旧产品以c-Δc-δrτ的单位可变成本生产再制造产品;最后，OEM和TPR分别以pn、pr的零售价格将新产品和再制造产品销售给顾客。

与本文相关的符号说明如下：i = η，r分别表示新产品和再制造产品。上标“b”和“u”分别表示再制造不受回收数量限制和受回收数量限制。上标“*”和“ ”分别表示OEM实施再制造设计和不实施再制造设计时的均衡解。用ΠO和ΠT分别表示OEM和TPR的利润。

c：无再制造设计时，单位新产品的生产成本;

Δc：无再制造设计时，单位再制造产品节约的成本，0 < Δc < c;

p1：第一周期单位新产品的零售价格;

q1：第一周期新产品的需求;

pi：第二周期单位新产品/再制造产品的零售价格;

qi：第二周期新产品/再制造产品的需求;

λ：废旧产品回收率，;

f：单位再制造产品专利费用;

δ：消费者购买再制造产品的偏好系数，0 < δ < 1;

τ：再制造设计努力程度;

k：再制造设计的成本系数[26];

δi：再制造设计为单位新产品/再制造产品带来的收益，0 < δi < 1。

（二）研究假设

为方便计算和分析，不失一般性，对模型做以下假设。

假设1：参与者在决策时信息透明，OEM和TPR均为风险中性且追求自身利润最大化。

假设2：两种产品在性能和质量上无差异，由于品牌效应，消费者对再制造产品的偏好程度低于新产品[27]。

假设3：借鉴文献[28][29]，设市场规模为1，消费者对新产品和再制造产品的支付意愿分别为v、δv，其中v服从[0，1]上的均匀分布。在第一周期，消费者购买新产品的效用函数为U1 = v - p1，可得第一周期新产品的需求函数为：

q1 = f（v）dv = 1 - p1（1）

在第二周期，消费者购买新产品和再制造产品的效用函数分别为：Un = v - pn，Ur = δv - pr。若v - pn≥δv - pr且v - pn≥0，即v≥，消费者购买新产品。若v - pn < δv - pr且δv - pn≥0，即≤v < ，消费者购买再制造产品。同理可得第二周期新产品和再制造产品的需求函数分别为：

qn =  f（v）dv = 1 - （2）

qr =  f（v）dv = （3）

假设4：为保证均衡解存在，参数k需要满足如下条件：

当再制造不受回收数量限制时，

k > δn2 + ;

当再制造受回收数量限制时，k >  。

三、模型建立及求解

OEM的利润函数如式（4）所示，第一项和第二项分别表示OEM在第一周期和第二周期销售新产品的利润，第三项表示OEM收取的专利费用，第四项表示OEM实施再制造设计投入的固定成本。TPR的利润函数如式（5）所示，第一项表示TPR销售再制造产品的利润，第二项表示TPR支出的专利费用。不等式（6）表示TPR在第二周期生产的再制造产品数量受其在第一周期末回收旧产品数量的限制。

ΠO = （δnτ - c + p1）q1 + （δnτ - c + pn）qn +

fqr - （4）

ΠT = （δrτ - Δc + pr）qr + fqr（5）

s.t.    qr < λq1（6）

博弈顺序如下：第一周期OEM决定单位新产品的零售价格和再制造设计努力程度;第二周期OEM首先决定单位再制造产品的专利费用，然后OEM和TPR同时分别决定单位新产品和再制造产品的零售价格，如图2所示。

定理1    OEM的利润函数是关于pn的凹函数，TPR的利润函数是关于pr的凹函数。

证明    将qn = 1 - ，qr = 代入式（4）和（5），求二阶偏导数可得： = < 0、 = - < 0，因此，OEM、TPR的利润函数分别是关于pn和pr的凹函数。

定理1    说明OEM和TPR都有使自己利润达到最大的价格决策。令 = 1 - δ > 0、1 = 1 - p1 > 0。

定理2    当λ≥λ′（τ，p1，f）时，qr < λq1约束成立，即再制造不受回收数量限制。此时，OEM和TPR的均衡价格决策分别为：

pnu（τ，f） = （7）

pru（τ，f） =

（8）

当λ < λ′（τ，p1，f）時，qr < λq1约束不成立，即再制造受回收数量限制。此时，OEM和TPR的均衡价格决策分别为：

pnb（τ，f，p1） = （9）

prb（τ，f，p1） = （10）

证明    为获得均衡价格决策，需要考虑qr < λq1和qr≥λq1两种情况。因此，构建如下拉格朗日函数：

Lr = （δrτ - c + Δc + pr）qr - fqr - μ（-λq1 + qr）（11）

进而得到如下KKT条件：

μ（-λq1 + qr） = 0

= 0

μ≥0（12）

情况1：当μ = 0时，结合 = 0、 = 0可得OEM和TPR的均衡价格决策，如式（7）和（8）所示。

情况2：当-λq1 + qr = 0时，联立λq1 = qr、 = 0、 = 0可得OEM和TPR的均衡價格决策，如式（9）和（10）所示。此时μ为：

μ =  + Δc

（13）

若qr≥λq1，则须μ > 0，因为 < 0，因此存在唯一零点为：

λ′（τ，p1，f） =

（14）

当且仅当λ < λ′（τ，p1，f）时，μ > 0;相反，如果λ≥λ′（τ，p1，f），则μ≤0，此时qr < λq1成立。

定理2表明，在两种情况下OEM和TPR的均衡价格决策是关于τ、f和p1的反应函数。由逆向归纳法得到其他均衡决策结果：

（1）当λ≥λ′（τ，p1，f）时，

p1u* = （15）

f u* = （16）

τu* =

（17）

pnu* =

（18）

pru* =

（19）

（2）当λ < λ′（τ，p1，f）时，

p1b* = （20）

τb* = （21）

f b* = （22）

pnb* = （23）

prb* = （24）

令τ = 0得出无再制造设计时的如下均衡决策：

四、模型分析

本节首先分析有、无再制造设计时TPR进入市场的边界条件，以及再制造成本节约对均衡决策和需求的影响;然后给出OEM的最优再制造设计策略，探讨再制造设计努力程度对均衡决策和需求的影响;最后考虑再制造设计的离散分布，令τ = 0和τ = 1分别表示低可再制造性和高可再制造性，得到OEM在再制造设计中选择高可再制造性的条件。

推论1  TPR进入市场的边界条件：

（1）当λ≥λ′（τ，p1，f）时，

1）若OEM不实施再制造设计，Δc > c;

2）若OEM实施再制造设计，

Δc > ;

当δr > δδn时，c > 。

（2）当λ < λ′（τ，p1，f）时，无论是否存在再制造设计，TPR进入市场始终有利可图。

证明    当λ≥λ′（τ，p1，f）且OEM实施再制造设计时，将式（18）和（19）代入式（6）后，令qru* > 0，得Δc > ，其他情况的证明类似，不再赘述。

推论1表明，当再制造不受回收数量限制时，只有当再制造成本节约大于某一阈值时，TPR才会选择进入市场。另外，当再制造设计为单位再制造产品带来的收益大于某一阈值时，OEM实施再制造设计更有助于推动再制造业发展。而当再制造受回收数量限制时，TPR往往会选择积极进入市场。这是因为，此时再制造产品的需求只与TPR回收旧产品的数量有关，所以只要OEM生产新产品，TPR就有利可图。

管理启示：TPR在进入市场前，除了要考虑市场中可回收的旧产品数量，还要考虑自己能从再制造设计中获得的收益。OEM可以通过改变再制造设计策略来阻止TPR进入市场。

推论2，再制造成本节约对均衡决策和需求的影响：

（1）当λ≥λ′（τ，p1，f）时，

1）若OEM不实施再制造设计， > 0; < 0; > 0; > 0; < 0; =  = 0;

2）若OEM实施再制造设计， > 0; > 0; < 0;当δr > 时， < 0， > 0;当δr < δδn时， < 0， > 0， < 0。

（2）当λ < λ′（τ，p1，f）时，无论是否存在再制造设计，均衡决策和需求都与再制造成本节约无关。

证明    当λ≥λ′（τ，p1，f）且OEM不实施再制造设计时， = > 0， = < 0， =  > 0， =  > 0， = - < 0，其中T = 8 + δ > 0，其他情况的证明类似，不再赘述。

推论2说明，当TPR掌握的再制造技术越熟练、节省的成本越多时，再制造产品的零售价格就越低、再制造产品的需求就越高。为了削弱TPR的竞争力，OEM会向TPR收取更多的专利费用。若OEM不实施再制造设计，其只能提高第二周期新产品的零售价格来增加产品的单位利润。若OEM实施再制造设计，当δr > （δn2δ + kδ）δn时，面对TPR的降价策略，OEM也会选择降低新产品的零售价格来抢占市场;当δr < δδn时，一方面OEM会降低再制造设计努力程度来避免再制造产品的生产成本进一步降低，另一方面OEM会提高第一周期新产品的零售价格来减少TPR回收旧产品的数量。当再制造受回收数量限制时，由于不存在价格竞争，因此均衡决策和需求与再制造成本节约无关。

管理启示  若OEM不实施再制造设计，面对TPR竞争力的提升，OEM只能选择提高专利费用和第二周期新产品的零售价格。若OEM实施再制造设计，其还可以通过降低再制造设计努力和第二周期新产品的零售价格及提高第一周期新产品的零售价格来缓解TPR的冲击。

推论3    OEM的最优再制造设计策略：

（1）当λ≥λ′（τ，p1，f）时，若再制造设计为两种产品带来的收益之比和再制造成本节约满足以下条件，OEM会选择实施再制造设计，

>

，

Δc <

<

，

Δc >

。

（2）当λ < λ′（τ，p1，f）时，OEM积极开展再制造设计。

证明  当λ≥λ′（τ，p1，f）时，若使τu* > 0，须令δn[δ（δ + 8 - 6c - cδ） - 2Δcδ]/2δr > c - Δc。令l = δ（δ + 8 - 6c - cδ） - 2Δcδ，当l > 0时，δn/δr > （2c - 2Δc）/l，反之，δn/δr < （2c - 2Δc）/l。当λ < λ′（τ，p1，f）时，由于δη（1 - c）（2 - λ2） > 0，因此τb* > 0恒成立。

推论3表明，当再制造不受回收数量限制时，以下两种情况下OEM会实施再制造设计。情况1：再制造成本节约小于某一阈值且再制造设计为两种产品带来的收益之比（下称收益比值）大于某一阈值时，再制造设计对OEM更有利。因此，OEM会自愿实施再制造设计。情况2：当再制造成本节约大于某一阈值时，即便再制造设计带给OEM的收益较小，OEM仍会实施再制造设计。因为此时的再制造成本节约达到了瓶颈，实施再制造设计更有助于缩小两种产品的成本差距。

当再制造受回收数量限制时，OEM积极开展再制造设计。通过观察τb*的表达式可以发现其大小与δr的取值无关。这是因为，此时再制造产品的需求取决于TPR回收旧产品的数量。因此，再制造产品的零售价格与第一周期新产品的零售价格有关，与其本身的生产成本无关。所以，再制造设计对TPR的定价决策没有直接影响，OEM会积极实施再制造设计，从而提高自己的产品竞争力。

管理启示    OEM可以根据收益比值和再制造成本节约来判断自己是否实施再制造设计。同时，TPR也可以适当降低废旧产品回收率来诱导OEM实施再制造设计。

推论4    OEM实施再制造设计时，再制造设计努力程度对均衡决策和需求的影响：

（1）当λ≥λ′（τ，p1，f）时，如表1所示。

（2）当λ < λ′（τ，p1，f）时， > 0; < 0; < 0; < 0; > 0;当0 < λ < 时， > 0。

证明过程与推论3的证明过程类似，不再赘述。

推论4表明，随着OEM对再制造设计的投入越来越大，其带来的成本节约也愈发明显，导致产品的零售价格降低。有趣的是，当再制造不受回收数量限制且δr < δδn时，即使降低再制造产品的零售价格，也无法增加其需求。这是因为随着再制造设计努力程度增大，新产品和再制造产品间的成本差距减小，导致TPR的降价幅度小于OEM的降价幅度，更多的消费者会选择购买新产品。相反，当再制造受回收数量限制时，由推论3可知，此时再制造产品的零售价格与第二周期新产品的零售价格无关，因此，降价策略可以有效刺激再制造产品的需求。

再制造设计努力程度对第二周期新产品的零售价格和需求影响比较复杂。当再制造不受回收数量限制且2/（3δ + 8） < δn/δr < 6/（8 - δ - δ2）时，由于生产成本的影响，OEM会为新产品制定较高的零售价格，导致新产品在与再制造产品的价格竞争中处于完全的劣势。因此，即使OEM选择降低新产品的零售价格也无法增加新产品的需求。当再制造受回收数量限制时，只有当TPR的回收率小于某一阈值时，再制造设计才有利于增加新产品的需求。这是因为此时市场上的再制造产品较少，更积极的再制造设计有利于提高OEM的核心竞争力，从而增加消费者对新产品的需求。

管理启示  当再制造不受回收数量限制时，OEM可以通过判断收益比值大小，决定提高或者降低再制造设计努力程度;对TPR而言，某些情况下再制造设计并不是有利的，如果再制造设计为单位再制造产品带来的收益较小，TPR应侧重降低生产成本，如缩短运输距离、改善工艺流程等，而不是一味地通过降低再制造产品的零售價格来追求更多的市场份额。另外，在TPR未进入市场时，OEM可以适当减少新产品的产量，达到限制TPR回收旧产品数量的目的。此时，即便OEM提高再制造设计努力程度进一步降低TPR的生产成本，也能保证自己在市场竞争中的优势。

推论5    当再制造设计成本系数满足以下条件时，OEM会在再制造设计中选择高可再制造性：

（1）当λ≥λ′（τ，p1，f）时，

δn2 +  < k < δn（δn + 2 - 2c） +

。

（2）当λ < λ′（τ，p1，f）时，

< k < 。

证明    当λ≥λ′（τ，p1，f）时，将τu* = 0代入OEM利润函数中得到Π[τu*][O];将τu* = 1代入OEM利润函数中得到Π[τu*=1][O]。若Π[τu*=1][O] > Π[τu*=0][O]，则OEM会在再制造设计中选择高可再制造性。令y = Π[τu*=1][O] - Π[τu*=0][O]  =  -  ，其中A = （δδn - δr）2，B = （cδ - Δc）。求关于k的一阶导数为 = - < 0，因此利润差y是关于k的单调递减函数。使得利润差为零的临界值k为：

ku* =  + δn（δn + 2 - 2c）（25）

结合假设4可知，当δn2 +  < k < ku*时，y > 0，OEM选择τu*  = 1。当λ < λ′（τ，p1，f）时，证明过程类似，不再赘述。

推论5表明，无论再制造是否受回收数量限制，只有当再制造设计成本系数小于某一阈值时，OEM才会在再制造设计中选择高可再制造性。不难理解，成本系数过高导致OEM的利润降低，从而削弱了OEM实施再制造设计的积极性。值得注意的是，当再制造不受回收数量限制时，随着再制造成本节约增大，OEM更倾向于在再制造设计中选择低可再制造性，从而降低TPR的成本优势。当再制造受回收数量限制时，由推论3可知此时不存在价格竞争，因此OEM会根据自己的利润来选择再制造设计策略。

管理启示  政府可以给予OEM适当补贴来激励OEM选择生产高可再制造性产品。当再制造成本节约较大时，TPR可以考虑主动承担部分再制造设计费用来进一步提高核心竞争力。

五、算例分析

本节借助数值算例分析再制造设计努力程度和再制造成本节约对供应链成员的利润影响，然后对边界回收率进行敏感性分析，最后研究当再制造不受回收数量限制时，δn和δr对均衡决策的影响。借鉴赵晓敏等[11]142和肖露等[25]1236，取c = 0.6、Δc = 0.3、δ = 0.7、k = 0.6。

（一）τ对OEM和TPR的利润影响

由推论4可知，如果收益比值所处的区间不同，再制造设计努力程度对均衡决策和需求的影响也可能不同。因此，选取四组δn和δr，使其比值分别处于推论4中的四个区间内，探讨τ对OEM和TPR的利润影响，结果如图3所示

由图3（a）可知，当再制造不受回收数量限制时，随着再制造设计努力程度增加，OEM的利润先上升后下降。因此，对OEM而言，虽然再制造设计有利于增加利润，但过高的再制造设计努力程度反而会损害其利润。图3（b）表明，TPR的利润的上升或下降趋势依赖于收益比值的大小。当收益比值较大时，再制造设计往往不利于TPR的发展。由推论4可知，随着再制造设计努力程度增加，再制造产品的需求减少、零售价格降低;同时，TPR支付的专利费用增加，TPR的利润会降低。

当再制造受回收数量限制时，四组δn和δr下得到的边界回收率分别为0.92，0.93，0.89，0.79。取低于临界点（0.7）作为再制造受回收限量时废旧产品的回收率。由图3可知，两种情况下OEM和TPR的利润变化趋势相似，差别在于变化速度不同。值得注意的是，當收益比值较大时，TPR从再制造设计中获得的收益较小;同时，OEM会向TPR收取更高的专利费用以弥补投入的再制造设计固定成本。这使得再制造产品尽管有一定的需求，但是TPR的利润仍会减小，甚至会面临亏损。

管理启示    无论再制造是否受回收数量限制，OEM都不宜投入过多的再制造设计。随着收益比值变大，虽然OEM能从再制造设计中获得更多收益，但是TPR支付的专利费用也会减少，因此OEM的利润不一定增加，而TPR的利润一定会随着收益比值的变大而降低。因此，当收益比值较大时，TPR应及时说服OEM调整再制造设计策略。

（二）对OEM和TPR的利润影响

取δn = 0.1、δr = 0.2、λ = 0.7分析再制造成本节约对OEM和TPR的利润影响。由图4可知，当再制造不受回收数量限制时，随着再制造成本节约的增加，OEM和TPR的利润均呈现先下降后上升的趋势。当再制造受回收数量限制时，OEM的利润不随再制造成本节约变化，TPR的利润与再制造成本节约成正比。

管理启示：当再制造不受回收数量限制且再制造成本节约较小时，OEM应当阻止TPR进入市场，否则，容易造成两败俱伤的局面。当再制造成本节约大于某一阈值时，OEM应当与TPR共同努力来提高再制造成本节约，例如，OEM设计易于拆卸、清理的产品，同时TPR不断改进再制造技术等。当再制造受回收数量限制时，OEM没有动机帮助TPR提高成本节约，并且如果再制造成本节约不够大，TPR的利润就会亏损。因此，TPR此时更应重视成本节约。

（三）敏感性分析

由上述分析可知，再制造受回收数量限制和不受回收数量限制两种情况下OEM的决策有很大不同，并且供应链成员的利润也有所差异。因此，本小节探讨边界回收率关于模型参数变化百分比的反应，结果如图5所示。

由图5可知，参数δ、c和Δc对边界回收率的影响显著，参数δn和δr对边界回收率的影响较为微弱。随着消费者对再制造产品的偏好程度增加，边界回收率显著提高，这是因为，此时再制造产品的需求增加，TPR需要从市场中尽可能多地回收废旧产品。此外，新产品生产成本的增加会降低边界回收率，再制造成本节约的增加会提高边界回收率。

管理启示    为推动再制造业的发展，一方面，OEM和TPR可以共同对再制造产品进行宣传来提高消费者对再制造产品的支付意愿。另一方面，OEM和TPR可以通过技术改革和再制造设计等手段来降低新产品和再制造产品生产成本。

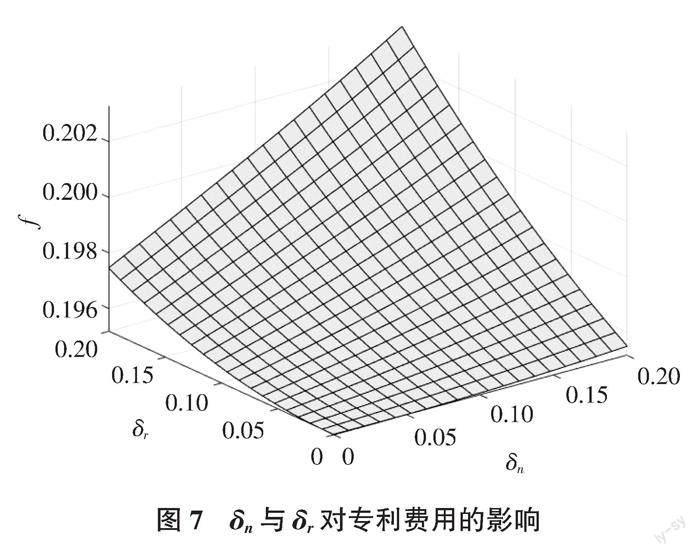
（四）δn与δr对再制造设计努力程度和专利费用的影响

通过图6和图7可知，再制造设计努力程度、单位专利费用都与δn或δr成正比。即，再制造设计为两种产品带来的收益越大，OEM投入的再制造设计努力程度越高，同时向TPR收取更多专利费用以弥补再制造设计的固定费用。

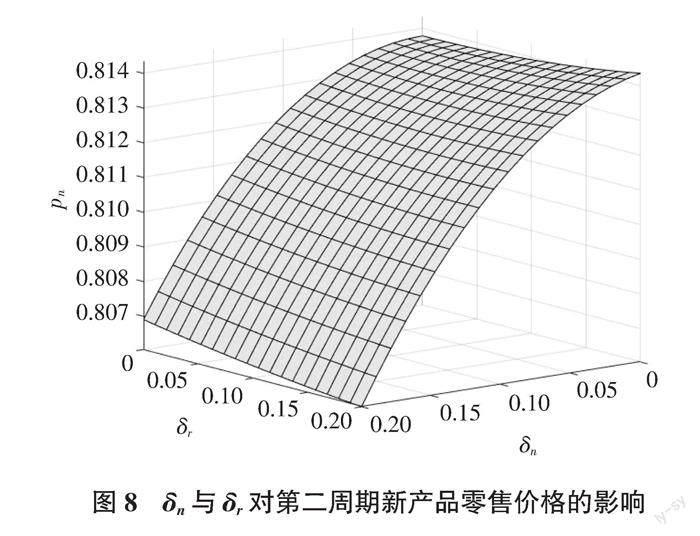
（五）δn与δr对第二周期新产品和再制造产品零售价格的影响

图8表明，在第二周期，新产品的零售价格与δn成反比。（1）当δn较小时，随着δr的增大，再制造产品的生产成本降低，导致其零售价格降低、需求增加。此时OEM会选择提高新产品的零售价格，从而降低新产品的需求来进一步增加再制造产品的需求，以损失部分市场份额为代价增加专利保护的额外收益。（2）当δn适中时，新产品的零售价格随着δr的增大先下降后上升。这是因为δr较小时新产品和再制造产品的成本差距较小，OEM有能力与TPR展开价格竞争;δr较大时再制造产品的成本优势较大，OEM会提高新产品的零售价格来收取更多的专利费用。（3）当δn较大时，再制造产品的零售价格随δr的增大而降低，此时再制造设计为新产品带来的收益较大。因此，OEM会降低新产品的零售价格来和TPR竞争市场。

图9表明，再制造产品的零售价格与δn或δr成反比。原因是，δn的增大最终导致新产品的零售价格降低，TPR只能采取降价策略来增加再制造产品的需求;δr的增大导致再制造产品的生产成本降低，使其零售价格降低。

管理启示  面对OEM的降价策略，TPR只能被动选择降低再制造产品的零售价格。如果TPR主动降低再制造产品的零售价格，OEM的首选策略仍是进行价格竞争。当OEM实施降价策略也无法增加新产品的需求时，OEM应提高新产品的零售价格，此举虽然增加了再制造产品的需求，但是OEM可以通过收取更多专利费用来弥补损失的市场份额。

六、结束语

本文基于授权再制造模式，考虑了OEM的再制造设计，构建了含有单个OEM和TPR的两周期动态博弈模型，得到了再制造受限制和不受限制情况下OEM和TPR的均衡决策和均衡利润。给出了OEM的最优再制造设计策略和TPR进入市场的边界条件，分析了再制造设计努力程度和再制造成本节约对决策结果的影响。利用数值算例讨论了再制造设计努力程度和再制造成本节约对OEM和TPR的利润影响，以及再制造设计带来的收益对均衡决策的影响。主要结论如下：

（1）当再制造不受回收数量限制时，OEM将根据收益比值和再制造成本节约决定是否实施再制造设计，只有当再制造成本节约大于某一阈值时，TPR才会进入市场。当再制造受回收数量限制时，OEM总是主动实施再制造设计，TPR总是积极进入市场。无论再制造是否受回收数量限制，只有当再制造设计成本系数小于某一阈值时，OEM才会选择生产高可再制造性的产品。

（2）当再制造不受回收数量限制且收益比值处于某一区间内（6/（8 - δ - δ2），1/δ）时，再制造设计不仅能降低两种产品的零售价格，还能增加两种产品的销量以及OEM和TPR的利润。此时OEM实施再制造设计有利于实现OEM和TPR共赢。

（3）虽然再制造设计可以提高OEM的利润，但是过高的再制造设计投入会产生高昂的再制造设计固定费用，反而导致OEM的利润下降，因此，OEM可以考虑逐步开展再制造设计。再制造设计不一定有利于TPR，当收益比值较大时，TPR甚至不希望OEM实施再制造设计。

（4）如果再制造不受回收数量限制，较高的再制造成本节约会增加TPR的竞争力，同时OEM也能获得更多的专利费用，从而增加自身利润，因此OEM和TPR应当共同努力降低再制造生产成本。如果再制造受回收数量限制，OEM获得的专利费用有限，没有动机帮助TPR提高成本节约。

基于本研究，未来可进一步扩展的研究方向为：其一是将消费者划分为绿色消费者和普通消费者，实践中，当再制造设计提高了产品的再制造水平时，绿色消费者由于环保意识会有更强的购买意愿。其二是可以考虑设置协调契约，探讨是否存在使OEM在不损失利益前提下提高再制造设计努力程度的供应链契约。

[参考文献]

[1]  Jin M Y，Nie J J，Yang F，et al. The impact of third-party remanufacturing on the forward supply chain： a blessing or a curse？[J]. International Journal of Production Research，2017，55（22）： 6871-6882.

[2]  Ke C，Jiang Z G，Zhang H，et al. An intelligent design for remanufacturing method based on vector space model and case-based reasoning[J]. Journal of Cleaner Production，2020，doi： 10.1016/j.jclepro.2020. 123269.

[3]  Marc R，Yu X，Yu Z. Managing a closed-loop supply chain with process innovation for remanufacturing[J]. European Journal of Operational Research，2019，276（2）： 510-518.

[4]  姚君，陳东彦. 基于市场努力与再制造过程创新的闭环供应链定价及协调策略[J]. 计算机集成制造系统，2021，27（11）： 3329-3340.

[5]  Zou Z B，Wang J J，Deng G S，et al. Third-party remanufacturing mode selection： outsourcing or authorization？[J]. Transportation Research Part E： Logistics and Transportation Review，2016，87： 1-19.

[6]  易余胤，阳小栋. 不同专利许可模式下的再制造闭环供应链模型[J]. 计算机集成制造系统，2014，20（9）： 2305-2312.

[7]  Qiao H K，Su Q. Distribution channel and licensing strategy choice considering consumer online reviews in a closed-loop supply chain[J]. Transportation Research Part E： Logistics and Transportation Review，2021，doi： 10.1016/J.TRE.2021.102338.

[8]  Hong X P，Govindan K，Xu L，et al. Quantity and collection decisions in a closed-loop supply chain with technology licensing[J]. European Journal of Operational Research，2017，256（3）： 820-829.

[9]  Zhao J J，Wang C X，Xu L. Decision for pricing，service，and recycling of closed-loop supply chains considering different remanufacturing roles and technology authorizations[J]. Computers & Industrial Engineering，2019，132： 59-73.

[10]  赵晓敏，孟潇潇. 授权模式下制造商与再制造商的演化博弈决策[J]. 中国管理科学，2021，29（2）： 129-136.

[11]  赵晓敏，孟潇潇，朱贺. 专利授权模式下OEM与再制造商的博弈决策： 基于OEM的绿色创新视角[J]. 管理评论，2020，32（4）.

[12]  Huang Y T，Wang Z J. Pricing and production decisions in a closed-loop supply chain considering strategic consumers and technology licensing[J]. International Journal of Production Research，2019，57（9）： 2847-2866.

[13]  李巍，张汉江，杨柳. 基于市场划分的再制造许可费对定价策略的影响[J]. 中国管理科学，2020，28（6）： 94-103.

[14]  郑本荣，杨超，杨珺. 专利保护下双渠道闭环供应链的定价与协调决策[J]. 系统工程学报，2017，32（1）： 103-113.

[15]  唐飞，许茂增. 考虑专利保护和渠道偏好的再制造双渠道闭环供应链决策与协调[J]. 运筹与管理，2019，28（6）： 61-69.

[16]  申成然，熊中楷，彭志强. 专利保护与政府补贴下再制造闭环供应链的决策和协调[J]. 管理工程学报，2013，27（3）： 132-138.

[17]  Zhang D Y，Zhang X M，Shi B，et al. Collection and remanufacturing of waste products under patent protection and government regulation[J]. Sustainability，2018，10（5）： 1402-1424.

[18]  夏西强，朱庆华. 外包再制造下再制造设计对制造/再制造影响[J]. 管理科学学报，2019，22（9）： 97-112.

[19]  夏西强，朱庆华. 主动再制造设计下制造/再制造博弈模型研究[J]. 系統工程学报，2018，33（3）： 328-340.

[20]  夏西强，朱庆华. 授权再制造视角下再制造设计对制造再制造影响研究[J]. 运筹与管理，2021，30（3）： 212-217.

[21]  Liu Z，Li K W，Li B Y，et al. Impact of product-design strategies on the operations of a closed-loop supply chain[J]. Transportation Research Part E： Logistics and Transportation Review，2019，124： 75-91.

[22]  Wu C H. OEM product design in a price competition with remanufactured product[J]. Omega，2013，41（2）： 287-298.

[23]  Wu C H. Product-design and pricing strategies with remanufacturing[J]. European Journal of Operational Research，2012，222（2）： 204-215.

[24]  曹晓刚，郑本荣，闻卉. 基于DFD的再制造系统生产及定价联合决策研究[J]. 管理工程学报，2016，30（1）： 117-123.

[25]  肖露，王先甲，钱桂生，等. 基于产品设计的再制造激励以及政府干预的影响[J]. 系统工程理论与实践，2017，37（5）.

[26]  张娟，王子玷月，余菲菲. 纵向供应链中新产品技术创新模式选择[J]. 管理学报，2020，17（11）： 1697-1705.

[27]  夏佳玉，马祖军. OEM代工模式下品牌厂商的再制造策略[J]. 工业工程与管理，2021，26（4）： 168-176.

[28]  Shang W，Ha A Y，Shilu Tong S. Information sharing in a supply chain with a common retailer[J]. Management Science，2015，62（1）： 245-263.

[29]  Chen X，Wang X J，Xia Y S. Production coopetition strategies for competing manufacturer that produce partially substitutable products[J]. Production and Operations Management，2019，28（6）： 1446-1464.

Decision of Closed-loop Supply Chain Considering Remanufacturing Design under the Authorization Mode

Wei Jie， Li Zhihao

（School of Economics and Management， Hebei University of Technology， Tianjin 300401， China）

Abstract： By considering the original equipment manufacturer′s （OEM′s） remanufacturing design under the authorization mode， we formulate a two-period dynamic game model of a closed-loop supply chain consisting of an OEM and a third-party remanufacturer （TPR）. Based on the model， we present the TPR′s remanufacturing conditions and the OEM′s optimal strategy of remanufacturing design in two scenarios where remanufacturing is unconstrained or constrained， and analyze the effect of remanufacturing design on the supply chain members′ profits. The results are as follows： When remanufacturing is unconstrained， the OEM′s optimal strategy of remanufacturing design depends on the ratio of benefits brought by two products′ remanufacturing design and cost savings from remanufacturing. In addition， when cost savings from remanufacturing is greater than a threshold， the TPR will develop remanufacturing business. When remanufacturing is constrained， the OEM's optimal strategy is implementing remanufacturing design， and the TPR always should develop remanufacturing business. Whether or not the remanufacturing is constrained， the suitable remanufacturing design effort can bring greater profit for the OEM， the remanufacturing design is not always advantageous to the TPR. The results offer some beneficial references for OEMs and TPRs to carry out remanufacturing design and enter the market.

Key words： closed-loop supply chain; authorization mode; remanufacturing design; dynamic game

收稿日期：2022-04-10

基金項目：国家自然科学基金项目（71971076）

作者简介：魏    杰（1975—），教授，博士，主要研究方向：供应链管理、可持续运营管理。