电子商务环境下闭环供应链定价策略探讨
2016-12-27祝凌燕
祝凌燕


内容摘要:本文研究了电子商务环境下具有实体渠道和网络渠道的闭环供应链定价与协调问题,分析比较了独立决策模型和集中决策模型下闭环供应链的最优价格和最优利润,提出了缓解渠道冲突的策略。研究表明:联合博弈决策比Stackelberg博弈决策更有效率,即该多渠道供应链的上下游成员可通过联合定价获得最优利润。
关键词:电子商务 闭环供应链 多渠道 定价策略
中图分类号:F713 文献标识码:A
引言
环境问题的凸显和产品回收再利用中蕴藏的经济机遇,驱使越来越多的企业实施闭环供应链战略。电子商务的迅猛发展,使得企业电子销售渠道和传统渠道的组合运营即双渠道销售模式逐渐成为主流。然而,电子商务环境下闭环供应链的上下游成员间利益的纵向冲突及不同渠道之间的横向冲突,成为企业面临的难题和挑战。因此,如何通过适宜的定价策略,来分配供应链的利润,解决冲突,达到供应链系统的整体优化,是电子商务环境下闭环供应链系统中的关键问题。
国内外文献述评
本文就近年来国内外对电子商务环境下闭环供应链管理的研究文献进行了梳理,在归类的基础上明确了以下主要研究方向:闭环供应链回收渠道设计、电子商务环境下闭环供应链协调方法研究、电子商务环境下闭环供应链定价策略研究。关于闭环供应链回收渠道设计方面的研究大多是根据Savaskan(2004)年发表在 Management Science 上的文章进行不断丰富和扩展。姚卫新(2004)又在电子商务环境下对闭环供应链的形式进行了补充,增加了制造商直销的情况。在协调方法研究方面,季磊磊等(2015)通过分析比较分散决策和集中决策下供应链系统成员的最优定价策略和收益状况,得出分散决策下的双渠道闭环供应链没有达到帕累托最优,供应链成员的利润仍有改进空间。赵礼强等(2014)为了解决双渠道的冲突并实现混合双渠道的协调,设计了电子渠道价格加批发价的合同,实现了双渠道供应链的协调。在定价策略研究方面,徐兵、吴明(2012)针对生产商负责网上直销、零售商负责网下零售且具有回收再制造功能的双渠道闭环供应链,建立了带均衡约束的两层规划模型,得到了三种回收模式下双渠道闭环分散式供应链的最优定价决策。唐秋生等(2012)为了解决MeRCRM闭环供应链中的电子直销与传统零售渠道间的冲突问题,建立了基于Stackelberg理论的MeRCRM数量折扣博弈模型。
综上所述,国内外目前对电子商务环境下多渠道问题的研究主要集中于传统供应链的定价策略与协调机制研究,忽略了逆向物流的影响及多渠道间的横向、纵向冲突管理和协调机制研究。基于此,本文构造了由一个主导制造商分别通过自身拥有的网络直销渠道和零售商控制的网络平台、实体渠道进行销售而形成的多渠道闭环供应链模型,着重探讨了该模型在不同利润决策模式下的均衡价格和利润,并通过数学仿真验证了分析的合理性。
电子商务环境下闭环供应链模型
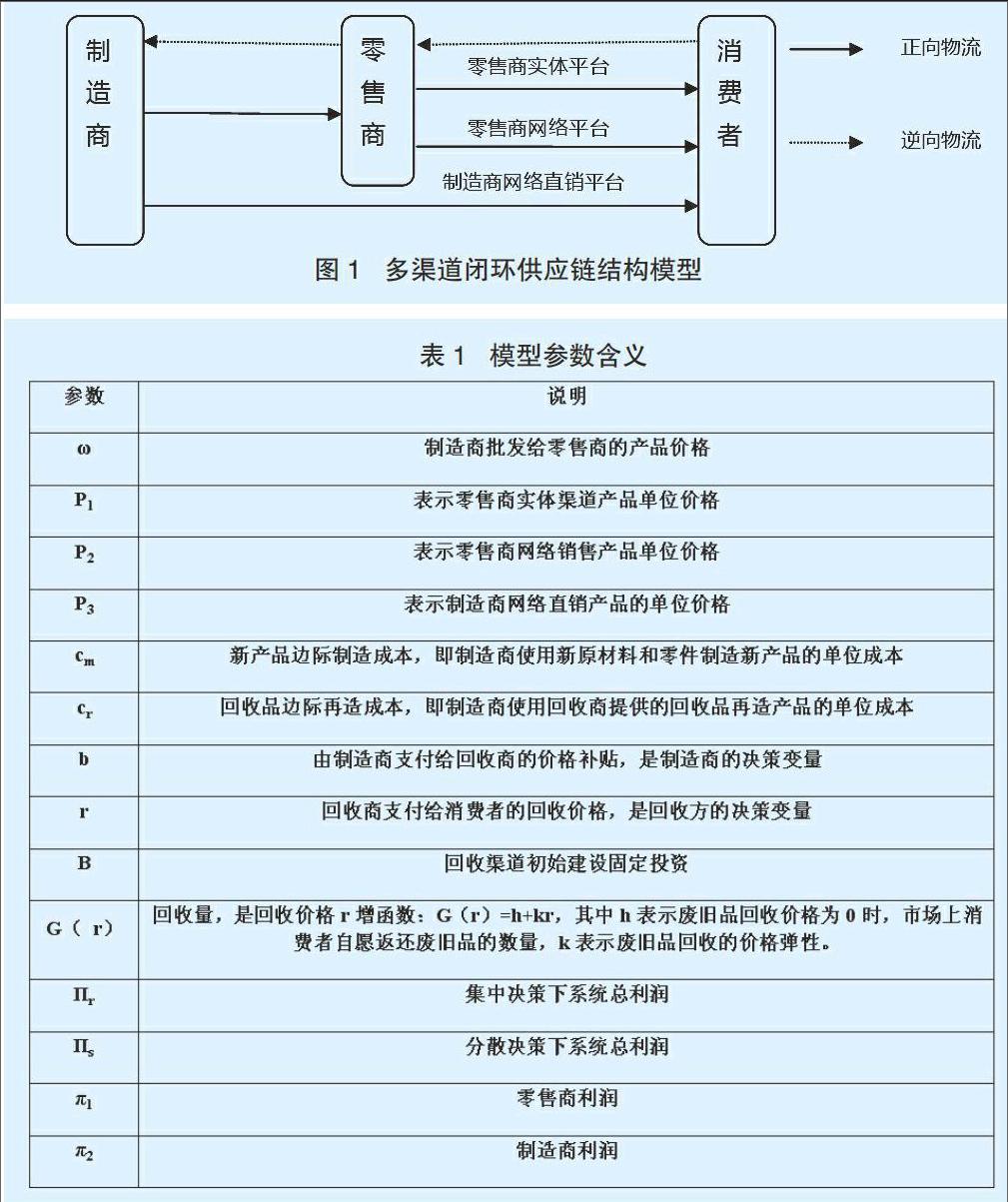
在竞争环境中,考虑一个制造商和一个零售商构成的闭环供应链模型,应首先考虑零售商庞大的销售网络和丰富的管理经验可降低回收成本,使制造商集中生产活动,所以应采用零售商回收的方式。模型描述见图1。参数说明见表1。基本假定如下:
第一,产品的需求是确定且线性的,并且新产品和再造产品对消费者的效用不存在差异。沿用以往学者分析模型中需求函数的形式,设零售商实体渠道、零售商网络平台与制造商网络直销渠道的需求函数分别为:
其中:a(a>0)为产品的市场总需求量;θ1和θ2(0<θ1,θ2<1)分别为消费者对零售商传统平台和网络渠道的偏好系数(即两种渠道所占的市场份额);α为销售渠道间的交叉价格弹性,其中0<α<1,因为多渠道内部任意渠道价格对自身需求的影响大于其它渠道价格对其需求的影响。
第二,单位再造品成本小于单位新产品成本,即0
第三,参数θ1,θ2,a,α,cr,cm,B,Δ已知并为共同知识。
第四,再造品与新品同质同值。
联合博弈决策模型(RD模型)
(一)联合博弈决策结果
在联合博弈决策下,制造商、零售商以整个闭环供应链系统的总利润为最终的目标,二者之间协商来确定各自的决策变量,整个系统的收入来自向消费者出售产品和再制造过程中的成本节约,其支出用于制造新产品的成本、回收废旧产品和处理不可再利用废旧品的费用。总利润函数如下:
利用 MATLAB7. 0,对目标方程式(4)求解r的一阶导数并令其等于0,得到:
对目标方程式(4)求解p1、p2、p3的一阶导数并令其等于0,得到目标利润函数Πr关于不同销售渠道销售价格p1、p2、p3的Hessian矩阵,记为D1:
因对于上述连续可微函数,当顺序主子式(-)kDk>0时,Hessian矩阵负定。由公式(6)易知,-|D31|=2>0,|D32|=4-4α2>0,-|D33|=-(1+α)2(1-2α),所以当时,Hessian矩阵负定,目标利润函数Πr为严格凹函数,有唯一最优解。
由,得到联合博弈决策下零售商的实体渠道最优价格、网络平台最优价格以及制造商的网络直销渠道最优价格分别为:
联合博弈下闭环供应链的最优利润为
(二)参数变化对决策结果的影响分析
基于上述的决策结果,本文从市场需求、成本、渠道偏好角度分析参数变化对决策结果的影响,以期获得一些管理方面的启示。
1.市场需求。推论1:当潜在市场需求量a增加时,零售商传统实体渠道价格、零售商网络渠道价格、制造商网络直销价格、零售商传统实体渠道需求、零售商网络渠道需求、制造商网络渠道需求、供应链系统总利润都随之增加。
证明:
推论1表明,随着电子商务的普及,制造商和零售商均可以考虑建立双渠道销售平台来增加产品的潜在需求。随着双渠道开通导致的市场需求量的增加,制造商、零售商的销售价格上调,闭环供应链系统的总利润也会随之增加。
2.产品成本。推论2:当新产品边际制造成本cm增加时,零售商传统实体渠道价格、零售商网络渠道价格、制造商的网络直销价格、回收商支付给消费者的回收价格r随之增加,制造商、零售商及系统的利润均减少。
证明:
推论2表明,生产成本的改善对供应链系统成员都是有利的。因此,在企业实际生产经营中,制造商应利用新技术等方式降低生产成本,下游的零售商也应该采取合作的态度,帮助制造商不断降低生产成本,这样不但增加了系统和各成员的利润,也增强了闭环供应链的竞争能力,这才是企业发展的利润之源。
3.销售渠道。推论3:当消费者对零售商传统平台偏好系数即θ1增加时,零售商传统平台的销售价格Pr1增加;当消费者对零售商网络平台偏好系数即θ2增加时,零售商网络平台的销售价格Pr2增加。证明:。
推论4:由知,当θ2>θ1 时,Pr2*> Pr1*;当θ1>θ2 时,Pr1*>Pr2*。
推论3、4表明,消费者销售渠道的偏好对销售渠道价格的制定有直接的影响。因此,商家应积极建立销售渠道,不仅会带来自身利润的增加,也会使供应链整体获利更大。
基于Stackelberg理论的独立决策模型(SD模型)
(一)基于Stackelberg理论的独立决策结果
在Stackelberg博弈决策框架下,制造商和零售商以最大化各自的利润为目标进行动态博弈,且制造商在博弈过程中占主导地位。决策过程如下:制造商首先确定制定批发价ω、价格补贴b和网络直销价格p3,零售商根据制造商的决策确定实体平台价格p1、网络平台价格p2和回收价格r。
制造商主导下,制造商的收入为批发产品给零售商的收入、网络渠道的收入及产品再制造过程中成本节约,其支出为制造成本和支付给零售商的回收补贴。零售商的收入包括两个渠道销售产品收入以及制造商支付的回收补贴,其支出为从消费者手中回收废旧品的费用。
根据主从对策原理,利用 MATLAB 7.0,首先对零售商的目标方程式求一阶导数。由易知,(14)
将公式(14)代入公式(11),并令易知, (15)
由π2关于p1、p2求导并令其等于0得到π2关于p1、p2的Hessian 矩阵 D2。由π1关于p3、w求导并令其等于0得到π1关于p3、w的Hessian 矩阵D3:
对于D2,易知-|D21|=2>0,|D22|=4-4α2>0,所以D2负定,目标利润函数π2为严格凹函数,有唯一最优解。对于D3,易知,,所以D3负定,目标利润函数π1为严格凹函数,有唯一最优解。
由联立,得到分散决策下零售商的实体渠道最优价格、网络平台最优价格和制造商的网络直销渠道最优价格、批发价格依次分别为:
将公式(10)-(13)代入总利润函数,可知分散决策下闭环供应链的最优利润:
(二)两种决策结果的分析比较
1.两种决策下的定价策略比较。
推论5:当满足a(θ1+θ2)+2(2α-1)cm>0时,Ps1*>Pr1*,Ps2*>Pr2*,Ps3*>Pr3*。即分散决策下的销售价格高于联合博弈决策下的销售价格。这说明联合博弈决策的闭环供应链更具有市场竞争力,联合博弈决策对消费者更有利。
2.两种决策下的系统利润比较。
由公式(14)和(21)进行比较:Πr>Πs。表明由于双重边际效用现象,制造商和零售商以各自的目标函数进行决策所得的闭环供应链的最优利润小于联合博弈决策下的最优利润。所以制造商和零售商可以通过适当分配合作利润,提高各自的利润水平。
以上两种结论说明了联合博弈决策比分散决策更有效率。因此,制造商和零售商可以通过尽力协调双方的决策,适当分配合作利润,提高各自的利润水平和系统的整体效率。
算例仿真
(一)联合博弈决策模型的算例分析
对于联合博弈决策模型,参数的取值范围及仿真结果如表2所示。
表2的仿真结果验证了推论3和推论4的结论,即销售渠道份额越大,相应渠道的销售价格越高。
(二)基于Stackelberg理论的独立决策模型算例分析
对于基于Stackelberg理论的独立决策模型,参数的取值范围及仿真结果如表3所示。
表3的仿真结果验证了推论5的结论,即当两种模型各参数的取值相同时,分散决策下的销售价格高于联合博弈决策下的销售价格。
结论
本文研究了在电子商务环境下由一个主导制造商分别通过自身拥有的网络直销渠道和零售商控制的网络平台及实体渠道进行销售而形成的多渠道的闭环供应链模型。通过分析比较基于Stackelberg理论的独立决策模型和联合博弈决策模型下闭环供应链的最优价格和最优利润,提出了缓解渠道冲突的策略,即联合博弈决策比分散决策更有效率,应加强供应链成员间的合作,使供应链各方及整体利润最优。
参考文献:
1.姚卫新.再制造条件下逆向物流回收模式的研究[J].管理科学,2004,17(1)
2.季磊磊,田大钢,慕飞飞.零售商双渠道下闭环供应链协调策略研究[J].技术与创新管理,2015,36(2)
3.赵礼强,徐家旺.基于电子市场的供应链双渠道冲突与协调的契约设计[J].中国管理科学,2014,22((5)
4.徐兵,吴明.双渠道闭环供应链的三种回收模式的建模分析[J].数学的实践与认识,2012,42(11)
5.唐秋生,牛婷婷,马先婷.基于Stackelberg理论的MeRCRM型闭环供应链批量折扣协调机制与定价策略[J].管理工程学报,2012,26(4)
