管式发射双鸭式布局导弹反安定面设计研究
2023-07-03浦钰文陈少松徐一航
浦钰文,陈少松,徐一航,魏 恺,孙 宁
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
筒式或箱式发射的鸭式布局导弹由于发射条件的限制,鸭舵的翼面尺寸和升力面积较小,导致其机动性和操纵性无法满足指标。而在鸭舵前添加一组翼面作为反安定面,即双鸭式布局,可以较好的改善这些问题。由于这组增设翼面在全弹头部,全弹压心前移,使得全弹在质心基本不变的情况下降低了全弹的静稳定性,增加了操纵性,导弹机动响应更快[1]。
目前,已面世的双鸭式布局弹箭有俄罗斯的“射手”AA-11导弹[2]、法国的“魔术”R550导弹、中国的PL-7导弹等,这些导弹的反安定面大多采用梯形翼、菱形翼等翼型。陆飞龙[3]和吕代龙[4]分别对两种梯形翼反安定面双鸭式布局模型的气动特性进行了研究。DAVARI等[5]和刘沛清等[6]分别研究简易前翼与主翼之间压力分布和近距耦合机理。但这些翼的展长不利于管式发射,为了对比研究不同反安定面对全弹气动特性的影响,本文提出了一种无侧缘的小展弦比边条翼反安定面。边条翼反安定面的前缘呈弧状,前缘母线与弹头母线相近,因此边条翼反安定面类似于大后掠角小展弦比三角翼,具有失速攻角大、高超音速下阻力小的特点[7-8],且随着后掠角增大分离涡越趋于长轴状[9]。当这种翼与后翼产生近距耦合作用时,由于边条涡在内侧,会对外侧涡产生诱导作用,使外涡趋于稳定[10]。
为了确定相同面积不同外形的反安定面对导弹气动特性的影响程度,采用数值计算方法,对鸭式布局模型、梯形翼反安定面双鸭式布局模型和边条翼反安定面双鸭式布局模型在不同马赫数和不同攻角下的气动特性进行对比研究。研究结论可为双鸭式布局导弹的结构设计提供指导。
1 计算模型与验证
1.1 计算模型与网格划分
在鸭式布局模型(M1模型,如图1所示)基础上,通过在鸭舵前添加一组矩形翼反安定面形成梯形翼双鸭式布局模型(M2模型,如图2所示),或添加边条翼反安定面形成边条翼双鸭式布局模型(M3模型,如图3所示)。梯形翼与边条翼反安定面面积一致,各模型鸭舵和反安定面与弹体均呈“×-×”型布局,模型弹体直径为D,模型弹长L=20D,反安定面与舵面厚度h=0.023 15D。图4为边条翼反安定面和鸭舵的位置与编号详细示意图,AC表示反安定面,BC表示鸭舵,文中舵偏角和攻角的正方向都以Y轴正方向为参考方向。数值模拟计算选取参考长度为L,参考面积选取S=πD2/4,参考坐标系取弹体系。压力远场静压101.325 kPa,静温288.15 K。

图1 鸭式布局模型示意图Fig.1 Canard configuration model
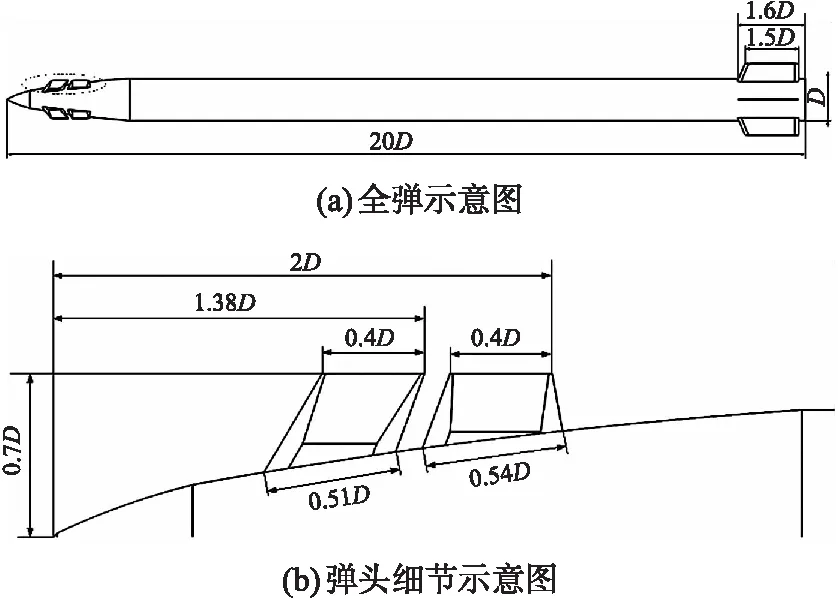
图2 梯形翼反安定面双鸭式布局模型示意图Fig.2 Split canard configuration model with trapezoidal split Canard
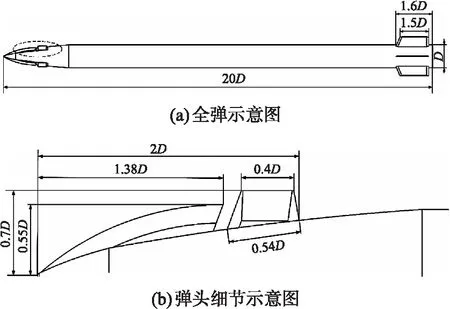
图3 边条翼反安定面双鸭式布局模型示意图Fig.3 Split canard configuration model owith striped split canard

图4 反安定面与鸭舵位置示意图Fig.4 Distribution of canard and split canard
本文计算域选用圆柱型计算域,流场长度20L,流场直径100D,由于反安定面与鸭舵区域结构复杂,因此借助Fluent Meshing网格划分软件进行全流场的多面体-六面体网格划分,并在剪切层和弹头涡流区域进行局部加密[11],网格如图5所示。

图5 网格划分示意图Fig.5 Grid divisions
1.2 数值模拟方法
流动控制方程为三维可压缩非定常Navier-Stokes方程,其积分形式可以写为
(1)
式中:V为控制体,∂V为包围控制体的封闭表面,S为控制体表面的面积,W为守恒变量矢量,FC为对流通量矢量,FV为黏性通量矢量。
本文采用了非定常计算中的双时间步法,其中物理时间描述实际运动,内迭代时间使计算收敛,二者皆采用隐式迭代求解。空间离散格式采用AUSM格式,迎风格式采用二阶迎风格式,对流通量应用Roe通量差分分裂。流体动力黏度采用萨瑟兰定律计算,并采用完全气体状态方程。
1.3 无关性验证
本文对M1模型划分了3套不同数量的网格进行网格无关性验证,分别为312万,492万和711万。来流工况为Ma=2.0,攻角α=10°,舵偏角δBC=0°,计算结果如表1所示。此外选取2.5×10-5s、5×10-5s和1×10-6s的时间步长进行时间步长无关性验证,结果如表2所示。表中CA为全弹轴向力,CN为全弹法向力系数,η为计算结果相对差值。
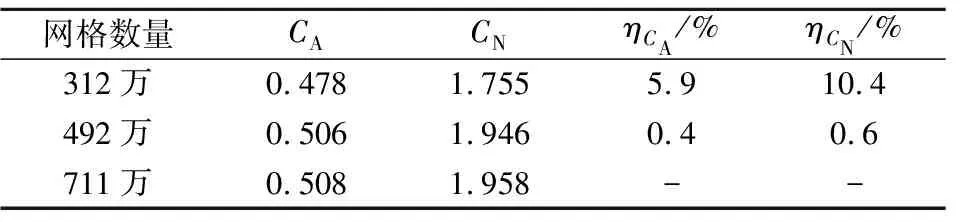
表1 网格无关性验证Table 1 Grid independence test
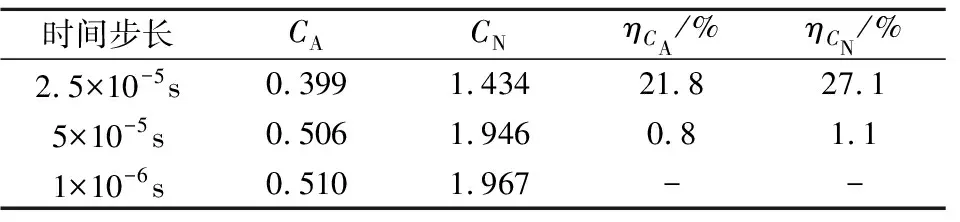
表2 时间步长无关性验证Table 2 Timestep independence test
由表1可知,711万网格量与312万网格量的计算数据相差较大,最大可达10.4%,但是与492万网格量的计算数据很相近,最大仅为0.6%,因此492万网格可以满足计算需求。
从表2可知,时间步长为1×10-6s与2.5×10-5s的计算结果相差最大为27.1%,但是与5×10-5s的计算结果相差不超过1.1%,因此本文时间步长选用5×10-5s。
1.4 各湍流模型对比
大涡模拟方法(LES)通过将湍流中的大尺度脉动和小尺度脉动分开处理,能够准确模拟复杂涡系间的流动特征。反安定面与鸭舵产生近距耦合作用时,边条涡与鸭舵涡系干扰机理复杂,因此选用大涡模拟作为湍流模型计算,亚格子模型采用WALE模型,模型网格量约为3 500万。验证模型选取M3模型,鸭舵舵偏角δBC=0°,远场边界为压力远场边界条件,模型边界条件设置为壁面无滑移边界条件,来流马赫数Ma=2.0,攻角α=0°~45°,质心系数为0.5。
但是大涡模拟方法对计算机的计算能力和储存能力要求极高,为了节省有限的计算资源,除大涡模拟外,还采用了S-A模型、k-ω模型和Transition SST模型三种不同的湍流模型进行对比,网格数量为492万。仿真结果如图6所示,在计算攻角范围内,Transition SST模型比其他两种模型更加吻合LES模型,因此本文选择Transition SST湍流模型进行后续计算,该湍流模型可以精确的模拟湍流附面层,对附着流动和分离流动可以给出合理结果[12]。

图6 大涡模拟及各湍流模型计算结果Fig.6 Simulation results of LES and turbulence models
1.5 数值方法验证
为了验证数值方法准确性,采用上述模拟方法对文献[13]中模型进行仿真,并与实验值进行对比。计算模型如图7所示,计算条件与实验一致,升力系数和俯仰力矩系数的对比结果如图8所示。升力系数和俯仰力矩系数曲线趋势一致,计算结果与实验值吻合度很高,数据偏差最大不超过5%,说明该数值模拟方法可靠。

图7 文献[13]验证模型Fig.7 Experimental model in Ref. [13]
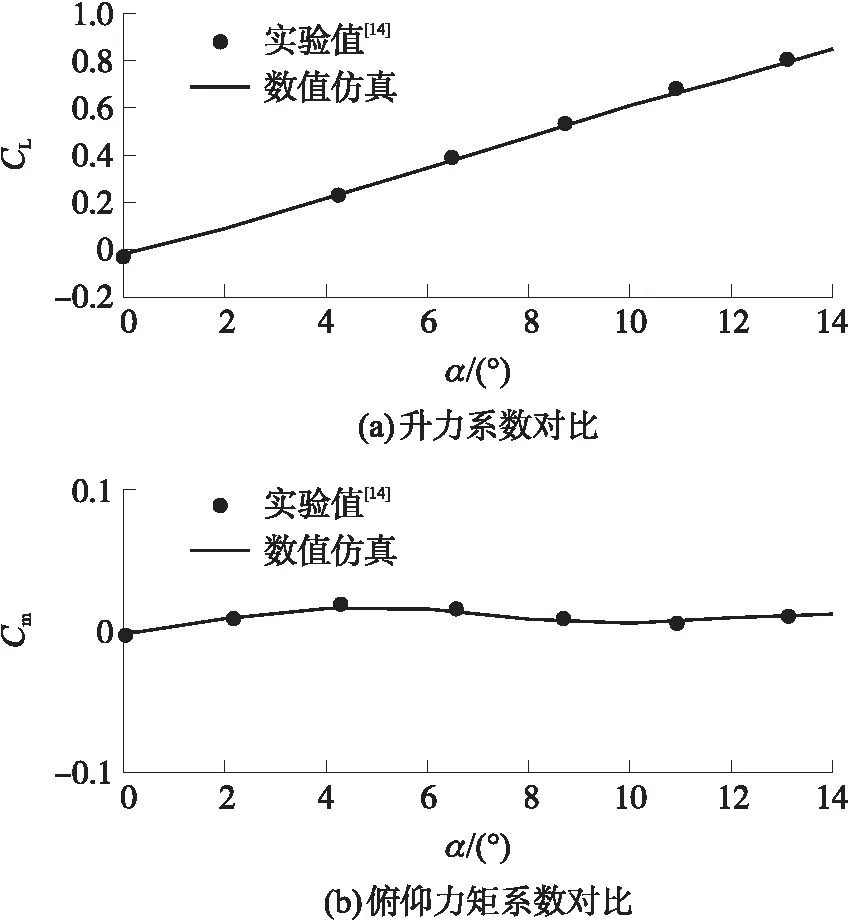
图8 升力系数与俯仰力矩系数对比图Fig.8 Comparison of lift coefficient and pitch moment coefficient
2 气动参数计算
2.1 亚音速下全弹气动特性
图9(a)所示为Ma=0.6,舵偏角δBC=0°工况下,全弹升力系数对阻力系数极曲线。攻角为0°~45°的范围内,在添加反安定面后,全弹的升力和阻力系数都有所增加,M2模型的升力系数在所有攻角范围内相较M1模型增大了6%~8%;M3模型的升力系数相较M1模型的除大攻角范围(α=30°~45°)增大6%~8%,其余攻角范围内只增大2%~3%。相较于M1模型,M2模型的阻力系数在所有攻角范围内增大5%~7%;M3模型的阻力系数在小攻角范围内(α=0°~30°)增长3%,其余攻角范围内增大9%。由于升力与阻力同时增大,M2和M3模型的全弹升阻比较M1模型差值不超过±1%。
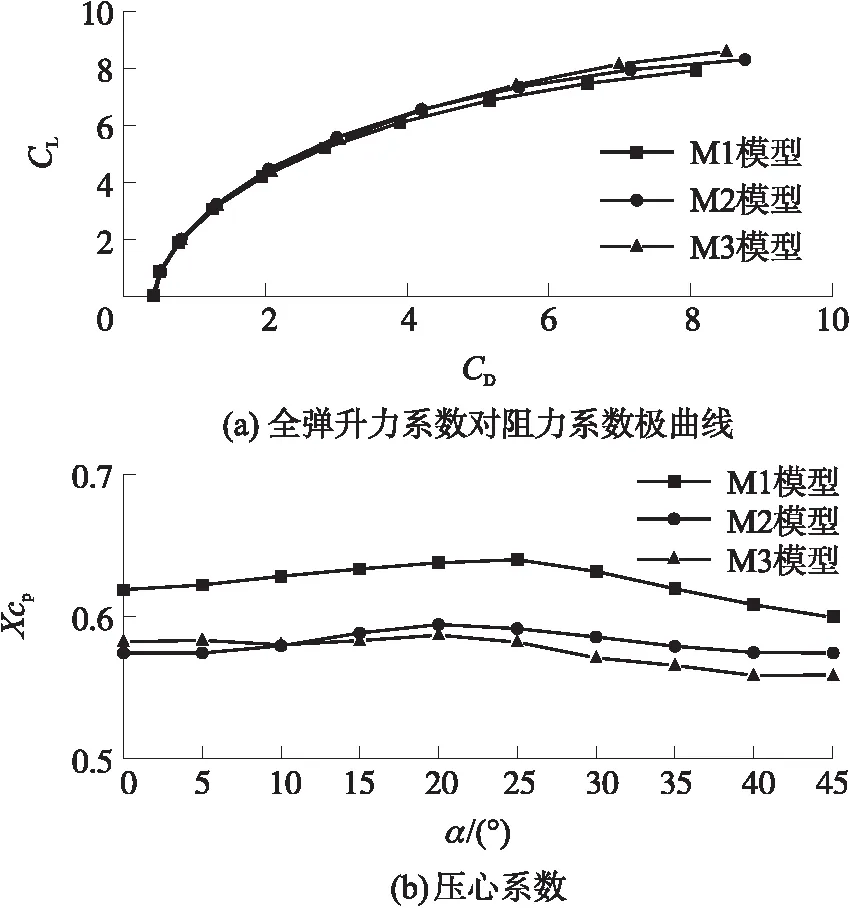
图9 Ma=0.6工况下全弹升力系数对阻力系数极曲线及压心系数变化图Fig.9 Lift coefficient to drag coefficient pole curve and pressure center coefficient at Ma=0.6
如图9(b)所示为该工况下全弹的压力系数变化图。可知在添加反安定后,压心前移,在α=0°~10°攻角范围内M2模型前移较多,最大为8%;在其余攻角范围内M3模型压心前移较多,最大为10%。
2.2 Ma=0.6时反安定面的影响分析
图10中,在增加反安定面后,M2和M3模型较M1模型所增加的升力系数ΔCL(如图10(a))要小于M2和M3模型中反安定面单独贡献的升力系数(如图10(b))。这是因为在添加反安定面后其他部件受其影响升力系数有所下降。

图10 Ma=0.6时全弹升力系数与反安定面升力系数对比Fig.10 Comparison of lift coefficients and anti-stability surface lift coefficient at Ma=0.6
3种模型在Ma=0.6工况下各部件升力系数如图11所示。可知,鸭舵和弹头的升力系数都受到影响。M2模型鸭舵升力系数较M1模型减小了18%~76%;M3模型鸭舵升力系数较M1模型的减小14%~44%。M3模型的弹头升力系数较M1模型减小10%~19%,但M2模型的降幅小于2%。

图11 Ma=0.6工况下各部件升力系数变化图Fig.11 Comparison of lift coefficient at Ma=0.6
弹头的压力分布受反安定面的影响显著。图12为Ma=0.6,α=20°工况下z=0平面的弹头表面负压力系数图,其中X为弹头长度。可以发现,M2和M3模型的弹头上下压力系数分布较M1模型的发生了较大变化,上下表面高压力系数差区域从M1模型中的鸭舵区域,转移至M2模型中的梯形翼反安定面位置和M3模型中的弹头鼻尖处。但是因为在圆锥弹头结构的原因,位置越靠前作用面积越小,导致M3模型弹头升力系数较M1模型的反而减小,而M2模型升力系数与M1模型相比基本不变。
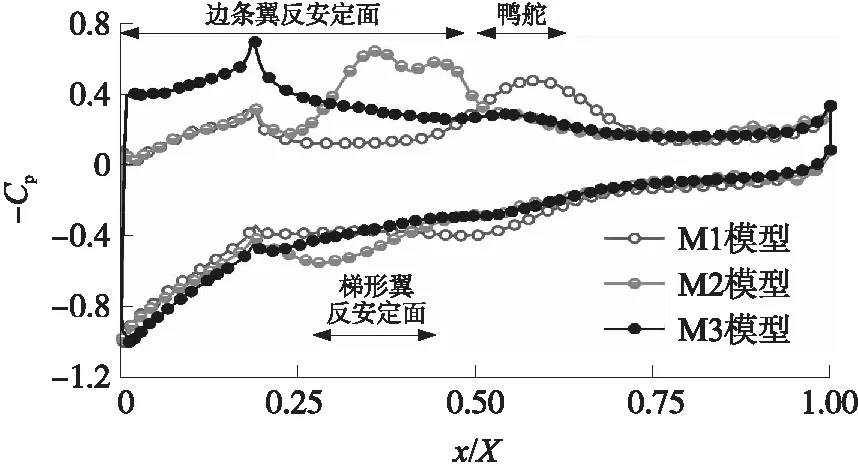
图12 Ma=0.6,α=20°工况下弹头在z=0平面表面负压力系数图Fig.12 Negative pressure coefficient of warhead at z=0 plane surface at Ma=0.6,α=20°
在图13中可以明显观察到各模型上洗流与舵面流态之间的差异。图中所示上洗流为背风舵BC1的主要来流,上洗流的形态可以直观显示舵面区域的当地攻角。通常随着当地攻角的减小,下表面压力系数和舵面前缘涡的强度降低,因而升力系数减小。
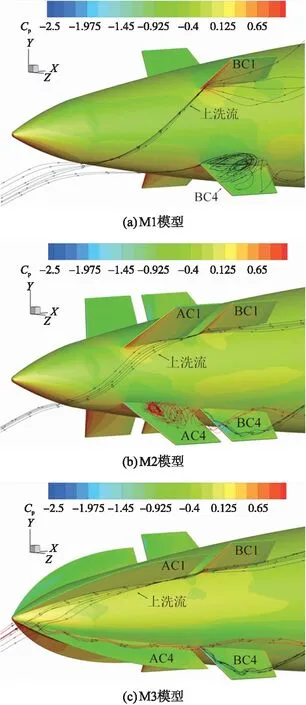
图13 Ma=0.6,α=20°工况下各模型反安定面和鸭舵上表面空间流线Fig.13 Space flow line of the split canard and canard at Ma=0.6,α=20°
相比于M1模型中的上洗流的起始位置和上洗流与BC1舵形成的夹角,M2模型中的上洗流起始位置由于反安定面AC4下的高压阻挡而提前,且上洗流会先流至AC1反安定面下,导致上洗流与BC1舵夹角减小。在M3模型中由于边条翼反安定面的弦长更长,反安定面下高压区更靠前,上述现象更为严重。迎风舵BC4的下表面来流也因为要先经过反安定面AC4,最后导致M2、M3模型中迎风舵当地攻角减小。因此,反安定面会一定程度的减小舵下表面的当地攻角而导致舵的升力系数减小,反安定弦长越长该影响越严重。
受反安定面的影响,既反安定面涡与鸭舵涡之间相互干扰,涡系干扰过程主要分为涡系诱导、涡系卷绕、涡系融合和涡量扩散[14]。
图13中各模型的BC4舵面流线反映出不同的干扰过程,其中M2模型中鸭舵前部发生涡系诱导,后部为卷绕融合扩散;而M3模型鸭舵面上主要发生涡系诱导到后缘时开始卷绕。反安定面分离涡与鸭舵涡发生涡系诱导的过程中,反安定面分离涡对涡内测区域产生下洗作用;对涡外侧区域产生有利的上洗作用。下洗会使当地攻角减小,气流分离点后移;上洗会使当地攻角增加,气流分离点前移[15]。受该诱导影响,M2、M3模型的舵面分离流没有形成如M1模型中的拱型涡,而是在靠近前缘与侧缘相接区域(反安定面涡外侧)形成局部强力分离涡。分离涡会在舵面产生低压和涡吸力,有利于增加升力系数,因而对于鸭舵来说诱导产生的鸭舵分离涡的作用面积和涡强度越大越好。M3模型中因为边条翼反安定面小展弦比大后掠角的特点,边条涡强度大且靠近内测,使上洗诱导作用强度和作用面积都要大于M2模型的,因此舵面分离涡的作用面积和涡强度也得到显著增强。
图14各模型舵面涡量图。对比M2、M3模型的反安定面分离涡在鸭舵上方强度分布,可以发现梯形翼反安定面分离涡强度整体上要低于边条翼反安定面分离涡,其至舵中后部分时已经开始破裂并且强度大幅度降低,而此时边条翼反安定面的分离涡还没开始破裂。在M3模型中,受边条翼反安定面分离涡影响,鸭舵涡核心的范围及强度都要大于M2模型,涡核离开鸭舵面的位置也比M3模型的要靠后。同时在非鸭舵涡作用区域,在边条翼反安定面分离涡的直接作用下,鸭舵表面涡的强度和涡作用区的厚度也要大于M2模型的,因而该区域的压力值也低于M2模型的,有利于增加舵面升力系数。

图14 Ma=0.6,α=20°工况下各模型鸭舵涡强度切片图Fig.14 Slices of canard vortex intensity for each model at Ma=0.6,α=20°
M2和M3模型舵面A剖面负压力系数示意图如图15所示。图中A剖面位置如图14所示,C为剖面弦长,A剖面位于鸭舵涡作用区,该剖面的负压力系数值可以反映出鸭舵涡的强度。在M3模型较强鸭舵涡的作用下,A剖面上表面大部分区域的负压力系数要大于M2模型。总之,当反安定面涡与鸭舵涡产生相互干扰作用时,反安定面涡的强度越强、位置越靠鸭舵根部,在鸭舵面上产生有利诱导作用的面积就越大,鸭舵涡的强度和在舵面的作用面积也会随之增大,舵面升力系数也会增加。

图15 Ma=0.6,α=20°工况下各模型鸭舵A剖面负压力系数示意图Fig.15 Negative pressure coefficient in the A-profile of canard at Ma=0.6,α=20°
2.3 超音速下全弹气动特性影响分析
如图16(a)为Ma=2,δBC=0°工况下全弹的升力系数对阻力系数极曲线。可知:在添加反安定面后,该工况下的全弹升力与阻力系数都有所增加。在所有攻角范围内,M2模型的升阻力系数在α=0°~20°范围内平均增加4%,其余攻角范围内平均增加1.5%左右;M3模型的升力系数在α=0°~10°范围内平均增加3%,其余攻角范围内增加1%,而阻力系数在所有攻角范围内只增加1%左右。因而,M2模型的升阻比较M1模型的在所有攻角范围内基本不变,而M3模型的升阻比较M1模型的在α=0°~10°范围内增加2%,其余攻角范围内不变。

图16 Ma=2.0和Ma=4.0工况下全弹升力系数对阻力系数极曲线及压心系数变化图Fig.16 Lift coefficient to drag coefficient pole curve and pressure center coefficient at Ma=2.0 and 4.0
如图16(b)为该工况下压心系数Xcp变化图,与Ma=0.6、α=20°左右时压心后移不同,Ma=2.0工况下所有模型在该攻角下压心位置均大幅度前移。此外,在添加反安定面后,在小攻角范围内,M2模型的压心前移8%,M3模型的压心前移5%。
当飞行速度提升至Ma=4时,边条翼反安定面小展弦比大后掠角的优势显现,Ma=4、δBC=0°工况下全弹的升力系数对阻力系数极曲线如图16(c)所示。在该工况下,α=0°~10°范围内M3和M2模型升力系数较M1模型分别增加7%和5%左右;阻力系数分别增加了1%和5%。因而,在该攻角范围内M3模型的升阻比比M1模型的增加7%,M2模型的只增加1%。
Ma=4、δBC=0°工况下全弹压心系数如图16(d)所示,α=0°~15°范围内M3模型的压心前移量超过M2模型的,较M1模型的压心前移9%。
2.4 Ma=2.0时反安定面的影响分析
图17为Ma=2.0工况下,反安定面及其余部件的升力系数变化图。可知Ma=2工况下各模型反安定面及鸭舵升力系数变化规律与Ma=0.6类似:梯形翼反安定面比边条翼反安定面在小攻角范围内的升力系数平均增加10%左右,但是边条翼反安定面的失速攻角和最大升力系数要大于梯形翼反安定面;M3模型中的鸭舵升力系数在很大攻角范围内都优于M2模型。
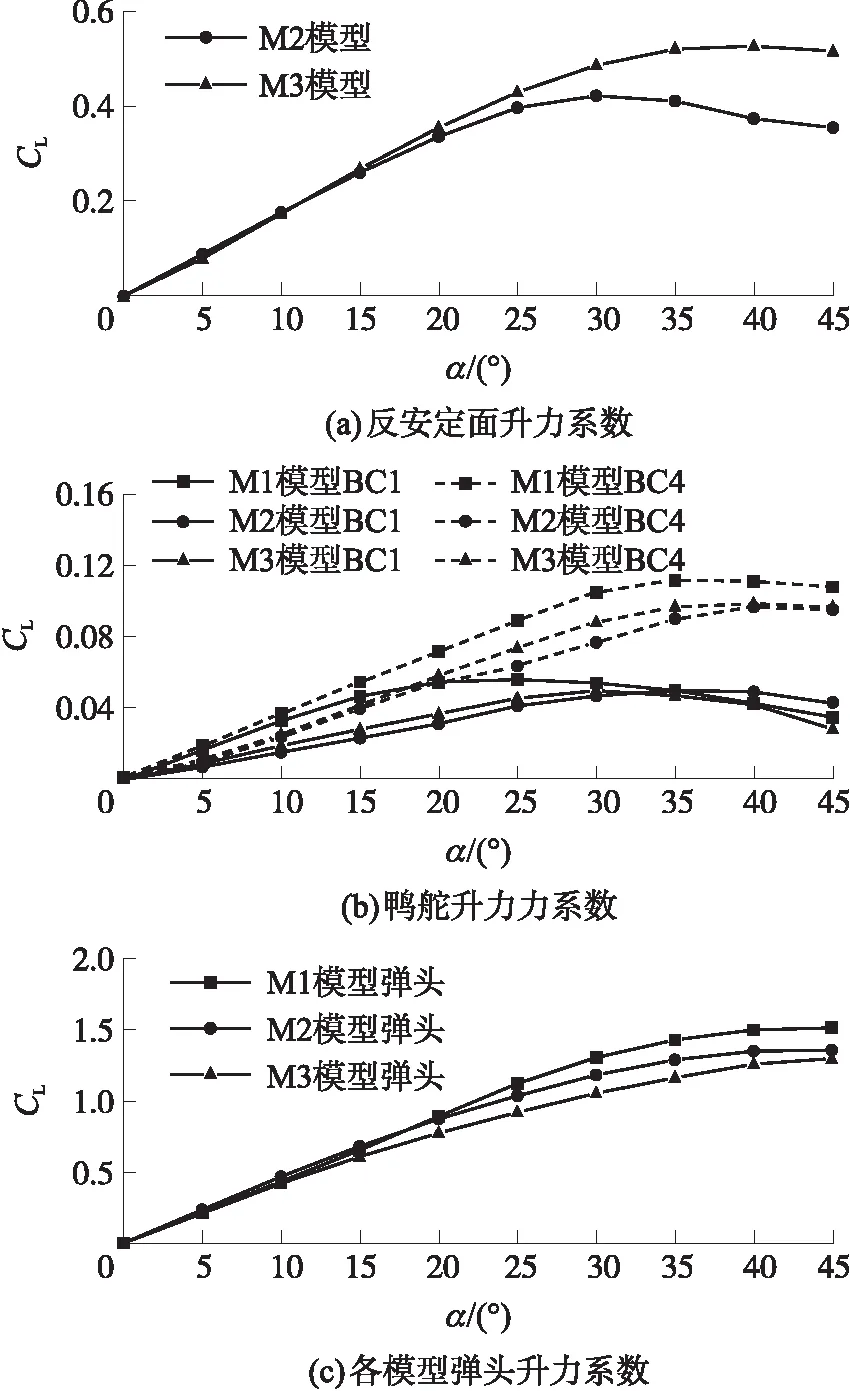
图17 Ma=2.0工况下各部件升力系数变化图Fig.17 Lift coefficient of each component at Ma=2.0
弹头升力系数的变化与亚音速工况下的变化趋势不同。在α=0°~15°范围内,M2模型弹头法向力系数增加了8%,M3模型弹头法向力系数减小了5%;其余攻角范围内,M2模型平均减小9%,M3模型平均减小了14%~19%。此时,梯形翼反安定面使弹头升力系数提升,而边条翼反安定面产生负作用,这也是两个模型压心系数产生差异的主要原因。因弹头升力系数变化规律较亚音速下有较大变化,因此以下着重分析其原因。
图18为Ma=2.0,α=10°工况下z=0截面的压力系数云图。可知,在M2模型中梯形翼反安定面明显强化了弹头上方低压区和下方高压区;反观M3模型弹头上方低压区被明显削弱,弹头下方虽然鼻尖下高压区作用范围及压力系数值增大但是舵下高压区被很大程度削弱。这反映了α=0°~15°范围内M2和M3模型弹头升力系数变化的原因。

图18 Ma=2.0,α=10°工况下z=0截面压力系数云图Fig.18 Cloud plot of pressure coefficient of z=0 section at Ma=2.0,α=10°
由于反安定面与背风舵膨胀波系的原因,M1和M2模型弹头上部产生了低压区。在有攻角时,超音速来流流至梯形翼反安定面或者鸭舵的前缘时遇到凸壁,气流受到阻档向上折转加速通过(如图19(a)和(b)所示)。由能量方程可知,该部分气流具有高速低压的特点,且在超音速条件下气流向上折转的扰动沿流向传递。在该部分气流越过前缘后,流通面积突然增大而形成膨胀波,使超音速来流继续加速降压,最后在反安定面、鸭舵与弹头上表面形成低压区,使弹头升力系数增加。反观M3模型(如图19(c)所示),因其小展弦比大后掠角的外形,气流沿边条翼反安定面流动时反安定面起到的凸壁作用很小,气流在沿轴向运动的过程中越过反安定面前缘形成较强的边条涡,带动周围气流使其旋转运动并以较强的轴向速度向后发展。该部分气流流动过程中流通面积没有经历突变,因此膨胀波强度较M1和M2模型的大幅减小,导致弹头上表面形成低压区的范围很小,使弹头升力系数减小。

图19 Ma=2.0,α=10°工况下反安定面及舵面空间流线图Fig.19 Space flow line of the split canard and canard in Ma=0.6,α=10°
在3个模型中弹头下部高压区产生的主要原因是反安定面与鸭舵产生的斜激波。而因为反安定面外形不同,各个模型波系有一定差异(如图20所示):M1和M2模型中激波位置主要在鸭舵和梯形翼反安定面前;M3模型中激波位置在弹头鼻锥与边条翼反安定面前端下方。在M1和M2模型中,超音速来流流经迎风面时,除弹头鼻锥之外,鸭舵和梯形翼反安定面对来流起到了直接的壅塞作用产生激波,而后激波使波后压力增加产生了高压区。但在M3模型中,超音速来流在流至弹头鼻锥处时在鼻锥和边条翼反安定面前缘阻挡,生成了远超M1和M2模型的头部激波,使鼻锥下高压区的压力系数值大于M1和M2模型的。但该部分气流在经过激波后被边条翼反安定面限制在AC3和AC4反安定面之间发展,又因边条翼反安定面弦长较长,气流在边条翼反安定面下流动发生过程较长,气流流向基本与边条翼反安定面平行。在边条翼反安定面的限制下,气流流至鸭舵前只会受到边条翼反安定面与鸭舵间膨胀波影响而轻微折转,无舵偏时气流到达鸭舵后与鸭舵间夹角较小,因而激波产生的壅塞度小,导致激波强度较M1和M2模型的有较大减小,鸭舵下因激波产生的高压区也减小。

图20 Ma=2.0,α=10°工况下z=-0.35D截面压力系数云图Fig.20 Cloud plot of pressure coefficient of z=-0.35D section in Ma=2.0,α=10°
3 全弹操纵性影响分析
图21为不同马赫数下δBC=10°时全弹俯仰力矩系数示意图,此时质心系数为0.5。在相同反安定面面积的情况下,亚音速时α=0°~13°攻角范围内,M2模型俯仰力矩系数减小较多,其余攻角范围内M3模型减小较多;M2模型平衡攻角增大3°,M3模型平衡攻角增大2°。此外,在亚音速工况下,M1和M2模型的俯仰力矩系数随着攻角增大而较小,但是M3模型在攻角达到α=30°后,俯仰力矩系数的变化会较小直到攻角达到40°。Ma=2.0工况下,除攻角α=37°~45°范围外,M2模型俯仰力矩系数减小较多,M2模型平衡攻角增大2°,M3模型平衡攻角增大1°。当马赫数增加至4.0后,M2和M3模型的俯仰特性非常接近,两者相较于M1模型的平衡攻角都增加了2°。
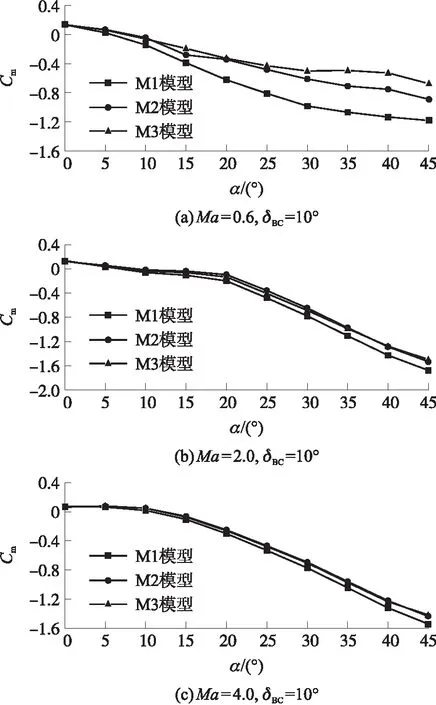
图21 不同工况下全弹俯仰力矩系数示意图Fig.21 Pitch moment coefficients at Ma=0.6, Ma=2.0 and Ma=4.0
4 总结
本文采用数值模拟方法对鸭式布局导弹及不同反安定面的双鸭式布局导弹不同工况下的气动特性进行研究,得到以下结论:
①在反安定面面积的相同情况下,Ma≤2.0时,中小攻角范围内M2模型除升阻比外的全弹升阻力系数增加量和压心前移量要大于M3模型的。此外,M2模型的弹头受干扰情况要优于M3模型。但当Ma>4后,M3模型的升阻特性和压心前移量要优于M2模型。
②反安定面,特别是边条翼反安定面,会抑制弹头上洗流,减小鸭舵当地攻角和舵下表面压力系数;在超音速工况下,梯形翼反安定面会产生较强的激波和膨胀波,而边条翼反安定面不会甚至会削弱鸭舵产生的波系。
③边条翼反安定面分离涡呈螺旋状且强度大,鸭舵涡在其诱导作用下强度和作用范围也增大,因而鸭舵上表面压力系数值减小。
④在添加反安定后,全弹压心系数前移,平衡攻角增大,M2模型在Ma=0.6工况下增加3°,Ma=2.0和Ma=4.0工况下增加2°;M3模型在Ma=0.6工况下增加2°,Ma=2.0工况下增加1°,在Ma=4.0工况下俯仰特性与M2模型相近,平衡攻角增加了2°。
