弹射救生火箭橇气动特性数值模拟及试验验证

解珍珍,董龙雷,李 康,胡云飞,张启洞

(1.西安交通大学 航天航空学院,陕西 西安 710049;2.中国兵器工业试验测试研究院,陕西 渭南 714200)

弹射救生是飞机出现故障或遭受破坏时保护飞行员安全逃生的重要手段[1]。自20世纪40年代以来,弹射救生组件已成为多种飞机的核心系统之一。目前针对弹射救生技术的主要研究方法包括飞行测试、理论分析、风洞试验、数值模拟、火箭橇试验等[2-4]。飞行测试危险且获得的数据有限;理论分析方法难以获得复杂形面(飞机)的流场;大批量的风洞试验成本过高,且无法进行全尺寸试验[5-7]。因此,高费效比的火箭橇试验成为弹射救生技术研究的主要途径。

国内外均有众多单位开展基于火箭橇的弹射救生技术研究。国外火箭橇研究比较广泛和深入,取得的成果包括开发了空气动力学仿真软件RSX(Rocket Sled Xpert),构建了专用火箭橇金属橡胶减震器,揭示了火箭发动机特性对火箭橇试验影响规律等[8-11]。国内火箭橇起步和研究较晚,主要开展了火箭橇理论、结构设计、弹道控制、数值模拟等方面研究,并取得了火箭橇新结构、揭示了地面效应原理等一些成果,有效促进了火箭橇技术的发展[12-14]。然而,国内外针对弹射救生火箭橇的气动特性研究较少,火箭橇试验对弹射座舱影响规律研究不足,尤其缺少气动力变化对弹射座舱弹射特性影响的研究。

本文基于计算流体力学方法,对弹射救生火箭橇气动特性进行数值模拟,获得火箭橇主要部分的气动阻力特性、运行速度对气动阻力影响规律,并开展火箭橇试验验证研究结论。

1 弹射救生火箭橇气动原理

弹射救生火箭橇试验是依靠火箭发动机推进的高速轨道试验,包括加速、巡航、减速、刹车等不同的运行阶段,其中巡航段是弹射救生试验的主要工作区间。火箭橇运行过程中的受力主要包括火箭发动机推力,橇体气动阻力和轨道摩擦阻力。气动阻力主要包括压差阻力和摩擦阻力两部分。在弹射救生火箭橇主要运行的亚音速和跨音速条件下,橇体气动阻力与空气密度、流速、湿度、温度、橇体形状等诸多因素有关,可采用式(1)近似计算。由于橇体运行过程中通常认为迎风面积和密度恒定,故可将式(1)等效代换,定义等效气动阻力如式(2)所示:

(1)

(2)

式中:Fa为气动阻力,v为风速,ρ为空气密度,A为迎风面积,C0为阻力系数,C*为等效阻力系数。

计算弹射救生火箭橇气动阻力时,空气阻力系数C0是一个综合影响系数,受速度、形状等参数影响。对于具体的弹射救生火箭橇试验,其值难以采用经验法或查表法等方式获得。因此,数值模拟是获得弹射救生火箭橇运行的实际气动阻力的有效手段。

弹射救生火箭橇的形状复杂、运行速度高,湍流模型对仿真结果有重要影响。常用湍流模型包括:单方程模型(Spalart-Allmaras)、双方程模型(k-ε、k-ω,SST)、雷诺应力模型和大涡模拟等[15-16]。本文以k-ε、k-ω,剪切压力传输(shear stress transport,SST)3种典型双方程模型作为研究对象。SST模型模型综合了k-ω模型在近壁区计算的优点和标准k-ε模型在远场计算的优点,适用性更好,其核心的湍流涡黏系数μt由式(3)获得[17]:

(3)

式中:a1为模型参数,k为湍流动能,ω为单位湍动能耗散率,S为应变率的不变测度,F2为一个混合函数。

2 仿真计算

2.1 数学模型

本文以弹射救生火箭橇为研究对象,基于流体仿真软件CFX中进行数值模拟。弹射救生火箭橇采用双轨道形式,单/双火箭发动机推进。火箭橇结构分为橇体、飞机座舱两个主要部分,其中火箭发动机、卡箍等其他构件合并进入橇体部分。

三维建模后,采用ICEM CFD软件对弹射救生火箭橇模型进行网格划分,结果如图1所示。以弹射救生火箭橇为中心的整体流场为扇形,尺寸为弹射救生火箭橇长度的10倍。弹射救生火箭橇模型的表面网格整体尺寸为8 mm,圆角、接头等布局网格细化。该网格模型以非结构四面体网格为主,通过网格无关性验证,选用的网格拓扑节点数约220万,网格单元规模约1 200万。

该仿真模型的入口马赫数Ma为0.4～1.0,温度为288. 15 K,大气压强为101 kPa。流动方向为正对火箭橇座舱(飞机机头),湍流强度为中等;火箭橇各部分与空气的接触面为绝热、无滑移的固体表面。

2.2 仿真结果及分析

2.2.1 仿真结果

以典型工况V=136 m/s(Ma=0.4)为例,计算的弹射救生火箭橇仿真模型的速度流线如图2所示。由图2可知,计算获得的速度流线平滑,亚音速条件下座舱下部通过的气流有效抑制了橇体尾部的湍流,减少了压差阻力。该工况下,火箭橇表面最大气动压力为10 kPa,最大速度位于火箭橇座舱顶端,为218 m/s。忽略振动冲击和气动压力,导轨与橇体之间垂直方向的作用力主要为橇体自重。由于火箭发动机燃料仅占橇体自重的一部分,可近似认为橇体与导轨的摩擦阻力恒定。因此,该火箭橇运行时的阻力变化基本由气动阻力决定。

图2 弹射救生火箭橇的速度流线(Ma=0.4)Fig.2 Velocity streamline of ejection life-saving rocket sled(Ma=0.4)

2.2.2 湍流模型影响

分别以136 m/s,238 m/s和340 m/s作为弹射救生火箭橇在亚音速和跨音速运动状态的典型工况,对比湍流模型对橇体气动阻力和等效阻力系数的影响,结果如图3所示。由图可知,采用SST模型,橇体在136 m/s、238 m/s和340 m/s的速度运行时,橇体总阻力分别为25.25 kN、84.65 kN和218.36 kN,各种湍流模型所得橇体阻力相差小于0.3 kN,相对误差小于1.2%;橇体等效阻力系数分别为1.37 N·s2/m2、1.49 N·s2/m2和1.89 N·s2/m2,各种湍流模型所得橇体等效阻力系数相差不超过0.02,相对偏差小于1.5%。由此可知基于3种双方程模型(k-ε、k-ω,SST)计算获得的数值模拟结果基本一致,而SST湍流模型的计算效率最高、耗时最少。

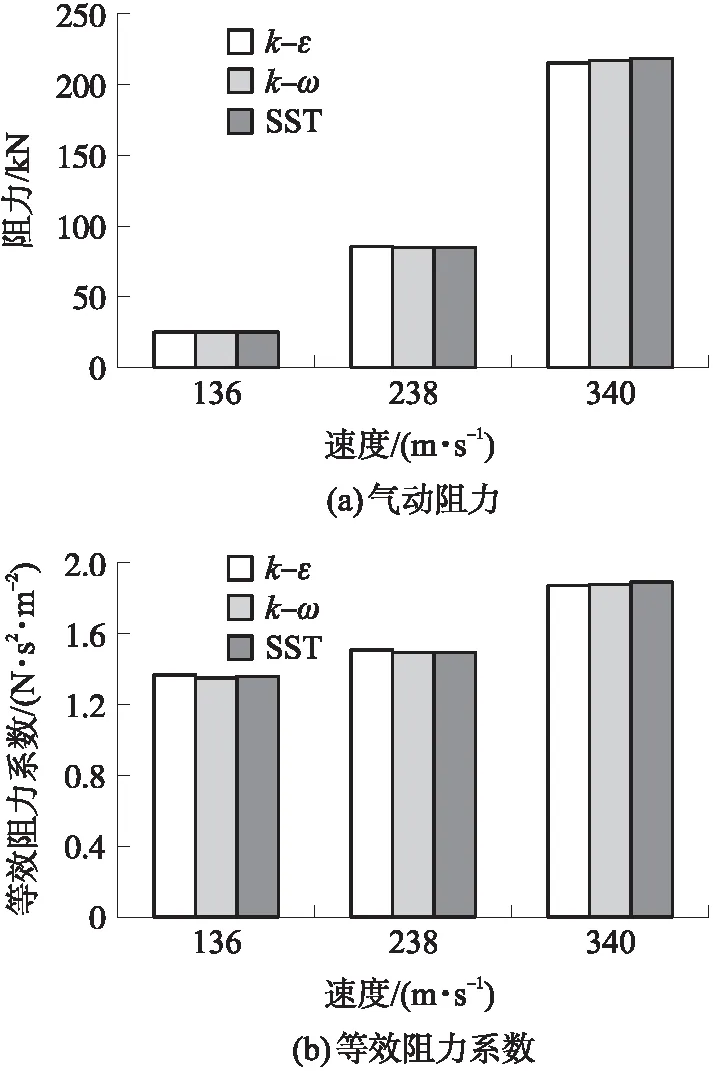
图3 不同湍流模型的气动阻力与等效阻力系数Fig.3 Aerodynamic drag and equivalent drag coefficient of different turbulence models

2.2.3 速度对阻力的影响

基于SST湍流模型,分析速度对弹射救生火箭橇阻力和等效阻力系数的影响规律,结果如图4所示。可知,弹射救生火箭橇的座舱阻力、橇体阻力及二者的合力都随着运行速度的增加而增大。座舱阻力显著小于橇体阻力。速度为136 m/s(Ma=0.4)时,座舱阻力、橇体阻力和阻力合力分别为4.78 kN,20.47 kN和25.25 kN。当速度340 m/s(Ma=1.0)时,各阻力均达到最大值,总阻力可达218.36 kN。

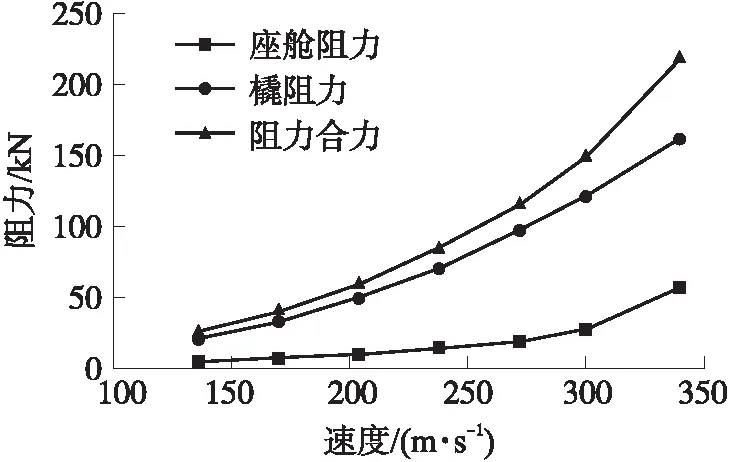
图4 火箭橇气动阻力与速度变化关系Fig.4 Relationship between aerodynamic drag and velocity variation of rocket sled

火箭橇橇体和座舱的气动阻力与速度的关系有明显差异。座舱与橇体的阻力比的变化规律如图5所示。速度在272 m/s以下,座舱阻力与橇体阻力的比值随着速度增加而缓慢减少,从136 m/s对应的0.23左右降至272 m/s对应的0.18左右。之后随着速度的提升比值快速增加,当速度达到340 m/s(Ma=1.0)时,比值达到最大,为0.35。这种气动特性变化主要源于橇体和座舱各自外形、与地面距离等影响。

图5 火箭橇橇体与座舱阻力的关系Fig.5 Relationship between rocket skid and cabin resistance

火箭橇等效阻力系数与速度的关系如图6所示。火箭橇等效阻力系数随着速度的增加而不断增大,火箭橇速度从136 m/s增加至340 m/s时,等效阻力系数从1.37增至1.89。气动阻力的非线性增加,源于速度增加导致的空气摩擦、空气压缩等变化。特别是弹射救生火箭橇迎风面压力与尾部湍流都随着速度显著增加。对于高速飞行器,其等效阻力系数在跨音速区间会出现极大值。而对于该弹射救生火箭橇,其等效阻力系数在音速以下随着速度增加而单调增大。

图6 火箭橇等效阻力系数与速度变化关系Fig.6 Relationship between equivalent drag coefficient and velocity of rocket sled

速度为340 m/s的弹射救生火箭橇的流场如图7所示。与图2相比,此时可清楚看到座舱尾部的大面积湍流。火箭橇迎风面、速度流场的分布规律未随速度发生明显变化,仅数值变大。空气流速为136 m/s时,火箭橇与空气间的最大相对速度为218 m/s,是空气流速的1.60倍;空气流速为340 m/s时,火箭橇与空气间的最大相对速度为498 m/s,是空气流速的1.46倍。最大相对速度与空气流速的比例未发生明显变化。因此,运行速度增加并未改变迎风面的流场分布规律。

图7 弹射救生火箭橇的速度流线(Ma=1.0)Fig.7 Velocity streamline of ejection life-saving rocket sled(Ma=1.0)

2.2.4 橇体对座舱影响

座舱由舱体和舱盖两部分组成,其中舱盖开启性能受表面压力的影响,是弹射救生的关键。为了揭示橇体运动对座舱表面压力的影响,以弹射救生火箭橇的运动反方向为阻力方向,以竖直向上为升力方向,分析橇体表面压力变化。座舱部位的阻力和升力如表1所示,火箭橇的橇体对座舱舱体影响较大,但对于舱盖的升力和阻力影响较小,差值分别为0.21 kN和3.20 kN,相对偏差为-15.33%和8.26%,舱盖气动特性受到橇体影响较小,满足弹射救生试验要求。

表1 弹射救生座舱带橇与不带橇的升、阻力Table 1 lift and resistance of ejection lifesaving cockpit with and without skid

采集舱盖上均匀分布的60个点的压力值,获得火箭橇橇体对座舱舱盖处的总压、静压和动压,结果如图8所示。舱盖的静压显著大于动压,且二者方向相反。通过静压与动压的叠加,舱盖的总压强的波动显著减轻,呈现均一化的特征。火箭橇引发的扰流对座舱表面产生了干扰,使得总压强的波动加强。橇体对舵盖各点动压的差值都小于15%,总压差值13%,静压差值小于20%。此外,带火箭橇的舱盖总压都略小于不带火箭橇的舱盖总压。

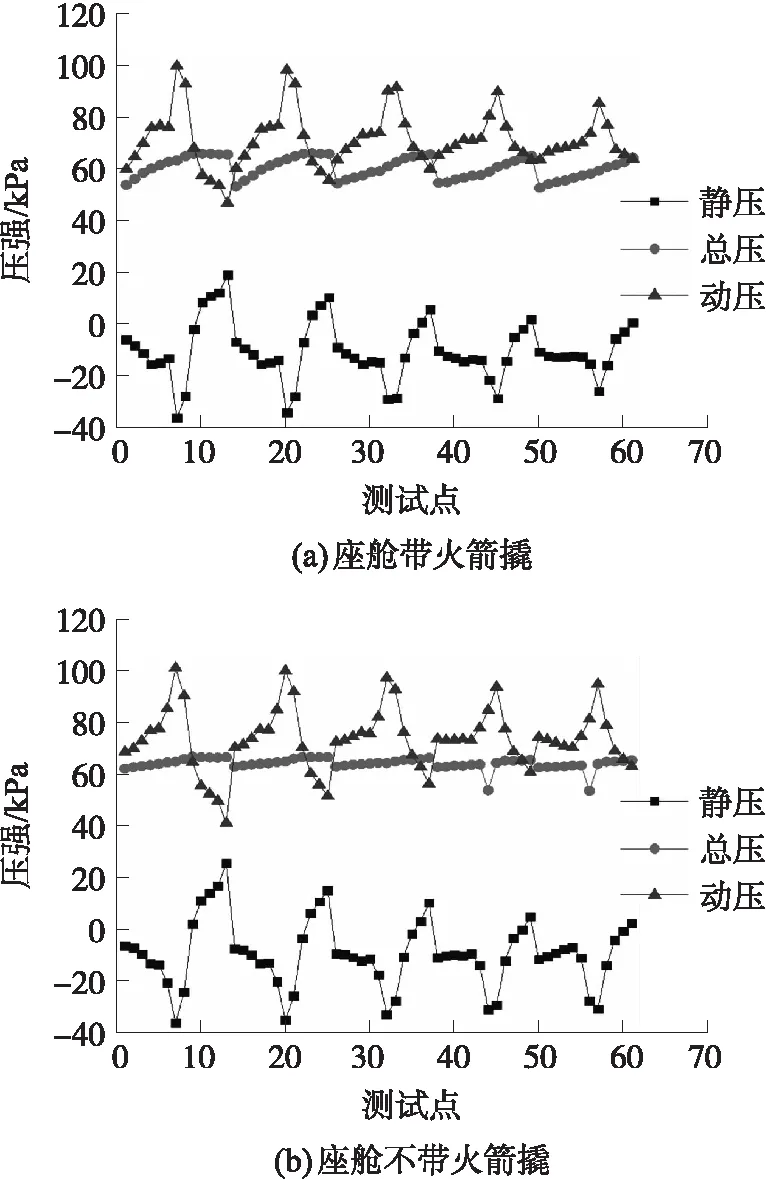
图8 弹射救生座舱舱盖压力数据Fig.8 Pressure data of ejection life-saving cockpit cover

舱盖表面的平均压力如表2所示。不带火箭橇的座舱平均静压、动压和总压分别为9336 Pa,64 033 Pa和73 369 Pa。与之相比,带火箭橇的舱盖处静压、动压和总压的均值的相对差值分别为13.95%、-5.88%和-3.36%。因此,弹射救生火箭橇试验能够有效模拟弹射救生舱的工作状态。

表2 弹射救生座舱舱盖带橇与不带橇的平均压强比较Table 2 Comparison of average pressure of ejection rescue cockpit canopy with and without skid

3 试验验证

以飞机座舱为研究对象,开展飞机弹射救生火箭橇试验,并对前文仿真结果进行验证。试验用火箭橇的结构、形状均与仿真模型相同。该弹射救生火箭橇以特制的火箭发动机推动,运行速度为亚音速。以相同配置进行2次火箭橇试验,其结果具有良好的一致性,取2次试验数据的均值进行研究。

基于数值模拟得到的弹射救生火箭橇气动阻力,设计了弹射救生火箭橇试验的弹道。采用经纬仪测得弹射救生火箭橇的试验弹道如图9所示,图中火箭橇的最大速度为303.3 m/s。

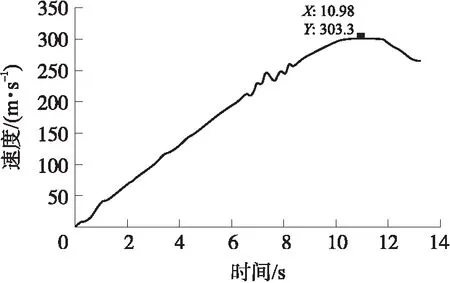
图9 弹射救生火箭橇试验弹道Fig.9 Sled test trajectory of ejection life-saving rocket

根据火箭橇试验测试数据拟合弹道,确定火箭橇真实运行的气动阻力。弹射救生火箭橇整体的气动阻力和等效阻力系数的仿真值与试验值对比如图10所示。火箭橇气动参数的仿真值和试验值基本一致,其中阻力最大差值仅为5.55 kN,最大相对偏差为6.4%;等效阻力系数最大偏差0.08 Ns2/m2,最大相对偏差为6.41%。因此,本文研究仿真结果可靠,方法可行。

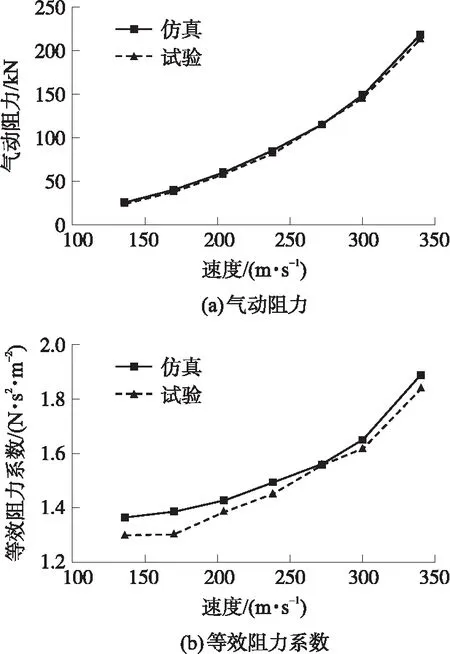
图10 仿真与试验对比Fig.10 Simulation and test comparison

4 结束语

本文以数值模拟和试验方法,研究了弹射救生火箭橇在亚音速和跨音速运行时的气动特性,获得了某型弹射救生火箭橇的气动特性规律,结果表明:

①湍流模型(k-ε、k-ω,SST)对弹射救生火箭橇数值模拟的结果影响较少,而SST湍流模型的计算效率最高、耗时最少。

②亚音速和跨音速条件下,弹射救生火箭橇的等效阻力系数随着速度增加而单调增大,火箭橇橇体和座舱阻力之比则呈现先减少后增加的规律。

③与无橇状态,火箭橇橇体对弹射救生座舱舱盖的阻力、升力及各点的压强影响均较小,相对偏差小于16%,火箭橇运行时产生的流场对座舱舱盖切割性能测试影响较小。