横流环境中高速射弹超空泡流及弹道特性数值分析

张程伟,贾会霞,周东辉,施红辉,王焯锴

(1.浙江理工大学 机械与自动控制学院,浙江 杭州 310018;2.西北工业大学宁波研究院,浙江 宁波 315100)

对于水下运动的物体,随着运动速度的增大,物体周围的压力随之降低,当压力降低到当地饱和蒸汽压力时,水会发生汽化,从而形成空泡。当空泡包裹住整个物体表面时,就形成了所谓的“超空泡”,此时物体受到的阻力明显下降,减阻最大可达90%以上[1]。因此,超空泡减阻技术在水下枪炮、水下高速鱼雷、反潜火箭、潜射导弹等兵器的设计中有着重要应用。

针对超空泡流动,国内外学者进行了大量的理论和实验研究。SAVCHENKO[2-3]基于LOGVINOVICH[4]提出的空泡截面扩张原理对超空泡物体在水中的高速运动进行了大量实验研究,进一步完善了超空泡形状的经验公式。VLASENKO[5]通过实验分别对亚音速和超音速条件下的空泡形态进行了分析,得到了可压缩性对超空泡流场的影响。TRUSCOTT等[6]通过对弹体小攻角入水进行实验,讨论了弹体形状及入水角对超空泡形态的影响。SARANJAM[7]通过实验和理论分析了水下航行体运动轨迹和空泡形状,并将六自由度(6DOF)刚体模型和NS方程耦合证实了此方法的准确性。曹伟等[8]通过高速射弹试验获得了空化数对超空泡形态特性和演化规律的影响。易文俊等[9]通过数值模拟分析了不同头型以及不同空化数下射弹在水中高速航行过程中超空泡形态特性。施红辉等[10-11]利用高速摄影技术对高速射弹水平入水进行了大量实验,分析了水深,弹体长径比对超空泡形状及弹体阻力系数的影响,并通过数值模拟研究了水下连发射弹超空泡之间的流动特性。张鹤等[12]通过高速射弹并联发射装置,开展了并联射弹水下实验,探讨了射弹之间不同间距,异步射弹发射对产生双空泡之间的影响。韩玉晶等[13]通过数值模拟对不同射弹间距和不同时间间隔的水下并联射弹进行了研究,对比分析了空泡的发展规律和射弹的弹道特性。袁馨等[14]对水下剪切来流中的超空泡射弹进行数值模拟研究,研究发现剪切来流下,空泡呈现不对称,剪切率增大,弹肩高速侧出现沾湿,阻力系数增加。

上述研究的水下环境都是静水,忽略了横流情况对空泡流动的影响。余德磊等[15]对横流情况下回转体并联入水进行数值模拟,分析了横流情况下回转体入水过程的空泡形态、流场及运动特性。李海东等人[16]通过数值模拟研究了横流扰动下超空泡鱼雷形态及水动力特性,分析了横流速度对鱼雷阻力的影响。WANG等[17]通过OpenFOAM软件数值模拟分析了横向速度对超空泡形态的演变,得到了相同的侧向流速下,对流速度越高,侧向流动对空腔廓形和阻力的影响越弱的结论。但上述研究没有考虑横流环境下射弹速度的自然衰减。

本文采用重叠网格和6DOF动网格技术模拟了射弹在不同横流速度下的自然衰减,分析横流条件对射弹空泡形态、弹体表面压力分布和弹道特性的影响。

1 数学方程

1.1 控制方程

超空泡射弹水下运动涉及气、液两相流动,本文数值计算采用VOF多相流模型求解水和水蒸气构成的多相流动系统。VOF多相流模型通过将水和水蒸气两相作为单一流体介质混合相处理,各相共用同一套动量方程,通过计算得到各相流体所占的体积分数,由此确定流动系统中各相的分布情况。

混合相的连续性方程和动量方程分别为

(1)

(2)

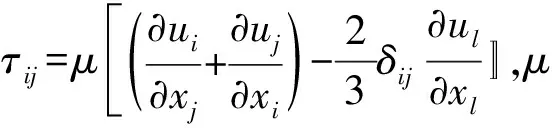
气液混合相的密度和黏度分别为

ρ=αvρv+(1-αv)ρl

(3)

μ=αvμv+(1-αv)μl

(4)

式中:αv为水蒸气相的体积分数,ρl、ρv分别为水和水蒸汽的密度;μl、μv分别为水和水蒸气的动力黏度。

1.2 湍流模型

本文采用RNGk-ε湍流模型[18],该湍流模型对于高速流动计算具有较高的准确性,近壁面采用标准壁面函数计算,湍动能k和耗散率ε的控制方程分别为

(5)

(6)

式中:μeff=μ+μt,μt为湍流黏度;αk、αε分别为k和ε的负向效应的普朗特数;Gk为速度梯度产生的湍动能;C1ε、C2ε为湍流动能耗散率的经验常数。

1.3 空化模型

本文采用Schnerr-Sauer空化模型[19]来描述超空泡流动中所涉及的汽相和液相之间的质量传递和能量传输,该模型具有较高的收敛速度和计算稳定性。其方程的一般形式为

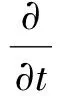
(7)

(8)

(9)

式中:vv为水蒸气相速度矢量,Re为蒸发速率,Rc为冷凝速率,rB为气核的半径,Pv为水的饱和蒸汽压力。

2 数值方法

2.1 计算模型

本文射弹几何模型源于文献[20]中的实验射弹,模型如图1所示。弹体为圆柱体,弹体的轴线为x方向,弹体在水中运动时,初始的速度方向也为x方向。弹体长L=36 mm,直径D=6 mm,长径比为6,质量为2.63 g。因为横流可能会影响弹体附着超空泡轮廓的对称性和造成弹体轨迹相对于轴线方向的偏移,本文采用三维模型开展数值模拟。

图1 射弹的物理模型Fig.1 Physical model of the projectile

射弹在水下运动产生空泡时,沿xoz截面截取如图2所示的二维空泡形态。

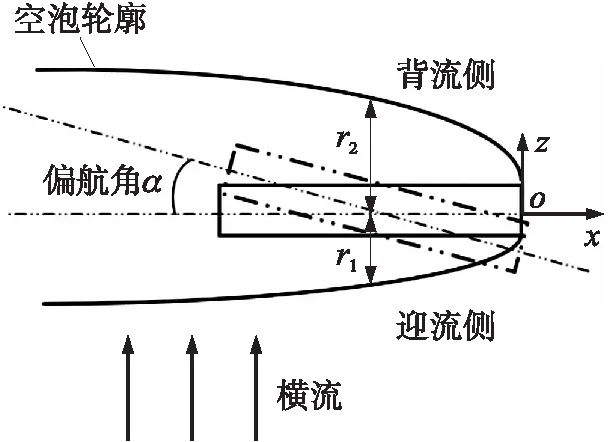
图2 超空泡形态参数Fig.2 Supercavitation morphological parameters

图2中,横流速度方向为z的正方向,直接接触横流的空泡轮廓一侧称为迎流侧,另一侧称为背流侧。定义弹体迎流侧空泡半径和背流侧空泡半径分别为r1和r2,弹体运动方向与x轴(即弹体初始速度方向)之间的夹角定义为偏航角α,弹体头部向z轴正方向(即远离迎流测)偏转为正,反之为负。

2.2 边界条件设置及网格划分

图3为计算域和边界条件示意图。弹体在流场中的运动通过重叠网格和6DOF技术来实现,整个计算域为550 mm×150 mm×150 mm(90D×25D×25D)的长方体区域,该计算区域可避免边界效应并满足射弹航道距离要求。前景网格为一直径为24 mm,长度为90 mm的圆柱体区域,两套网格重叠区域部分通过插值计算从而实现数据交换。计算区域采用结构化网格进行划分,为保证数据交换精度,重叠部分进行网格加密。图4为xoy平面内的二维网格示意图。迎流面设置为速度入口,其他计算域外边界设置为压力出口,弹体表面设置为壁面。计算模型中压力速度耦合求解采用Coupled算法,压力场空间离散化采用PRESTO!算法,体积率离散采用Modified HRIC,计算时间步长为1×10-6s。

图3 计算域和边界条件Fig.3 Computational domain and boundary conditions

图4 xoy平面内的二维网格示意图Fig.4 Schematic diagram of the two-dimensional grid in the xoy plane

2.3 数值方法有效性验证

为了验证本文数值方法的有效性,采用文献[20]中工况1进行验证,工况1采用的射弹模型和图1所示的射弹模型相同,初速度为76.42 m/s,水深为90 mm。对比结果如图5所示,从图中可看出数值计算结果和实验结果的超空泡轮廓和大小基本一致,数值计算结果略小于实验结果,最大误差约4.3%。

图5 t=3 ms时数值计算和实验结果对比图Fig.5 Comparison of numerical calculation and experimental results at t=3 ms

2.4 网格无关性验证

为了验证网格无关性,分别建立3种不同密度的网格,网格数分别为60万、110万、150万,计算时间步长为1×10-6s,采用图1射弹模型,分别用上述3种不同的网格密度对初速度为80 m/s的水下射弹进行数值模拟。射弹速度随时间变化曲线如图6所示。可以看出,随着网格数加大,150万网格和110万网格射弹速度变化规律几乎一致,60万网格速度下降较快,考虑在保证计算精度的情况下,为提高计算效率,本文采用110万网格进行数值计算。

图6 网格无关性验证Fig.6 Grid independence test

3 数值结果与分析

在不考虑水深条件下,本文以初始速度为70 m/s的射弹为例,对横流速度Vf为3 m/s,6 m/s和9 m/s的3种工况进行数值模拟,对比分析横流速度对超空泡的演化过程、流场分布特性和弹体的弹道特性影响。

3.1 超空泡形态特性分析

横流情况下水下射弹的超空泡演化过程较为复杂。图7为不同横流速度下空泡的演化过程,图中黑色代表水相,白色代表气相。横流的方向从下方指向上方。从图中可看到,由于横流的作用,空泡向背流一侧倾斜,不再对称。

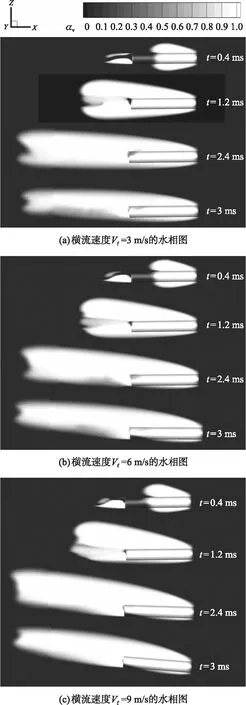
图7 不同横流速度下超空泡演化过程图(xoz平面)Fig.7 Evolution of supercavitation under different cross-flow velocities(xoz plane)

由图7(a)可知,横流速度为3 m/s时,在t=0.4 ms时的初始阶段,超空泡首先在弹体的肩部和尾部出现,受横流影响,弹体肩部和尾部的空泡都呈现不对称特征。对于肩部空泡,背流侧半径大于迎流侧;而在尾部,背流侧空泡的尺寸要小于迎流测的空泡。在t=1.2 ms时,肩部空泡和尾部空泡都发展变大,趋于形成一个覆盖整个弹体的超空泡。但受横流影响,背流侧尾部空泡和肩部空泡没有完全融合,在尾部靠近背流侧产生射流现象,随着时间推移,射流区域逐渐变小。在t=2.4 ms时,空泡的长度已达弹体尺寸的2.5倍左右。随着弹体的运动,受流动阻力影响弹体速度逐渐衰减,在t=3.0 ms时刻,空泡的尺寸基本稳定。

从图7中可看出,横流速度越大,在迎流测射弹尾部出现沾湿现象时间点越早,这必然会造成弹体负载的变化,从而影响弹体的运动轨迹。在图7(a)中横流速度为3 m/s,t=3 ms时未出现沾湿现象;图7(b)横流速度为6 m/s,t=3 ms时射弹尾部已经出现沾湿尾;而在图7(c)横流速度为9 m/s时,t=2.4 ms时就已经出现沾湿现象,t=3 ms时尾部沾湿状态持续,可观察到射弹此时发生偏转。

图8为横流速度对空泡半径的影响。从图中可看出,同一横流速度影响下,迎流侧空泡半径r1受横流影响,半径减小,背流侧空泡半径r2则相对比较稳定;同一时刻下,横流速度越大,迎流侧空泡半径r1越小,背流侧空泡半径r2越大,空泡越不对称。

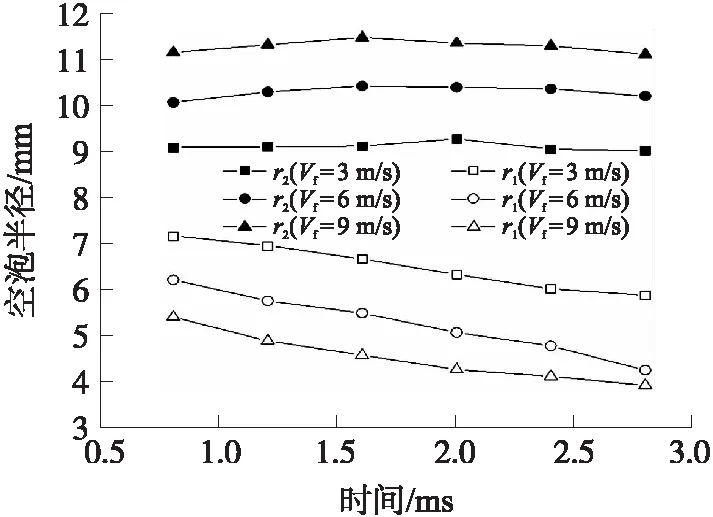
图8 不同横流速度下空泡半径对比图Fig.8 Comparison of cavity radii at different cross-flow velocities

3.2 弹体表面的压力分布变化

弹体表面的压力分布与弹体所受到的作用力密切相关。图9是不同时刻射弹头部压力分布曲线图,以横坐标原点为射弹头部中心点,负方向为迎流一侧,正方向为背流侧一端,图中P0为标准大气压。

图9 不同横流速度对头部压力分布图的影响Fig.9 Effect of cross-flow velocity on head pressure

初始阶段(t=0.4 ms),头部压力分布比较对称,头部中心点达到压力最大值,中心点两侧呈递减趋势,到达头部两端急剧下降;随时间推移,头部压力的最大值从0.4 ms时约18倍大气压逐渐降低为2.4 ms时不到8倍大气压;并且射弹持续受横流影响,头部压力分布越不均匀对称,射弹头部压力的最大值从头部中心点逐渐向迎流侧一端移动。

结合图9(b)和图9(d),可以看出,当横流速度不断变大,头部的最大压力值越大,并且压力的最大值也越靠近迎流侧一端。

弹体水下高速运动时,随着时间推移,空泡逐渐包裹弹体,只有头部一直处于沾湿状态。当横流速度不同时,弹体尾部在会先后出现再沾湿,造成弹体表面压力的变化。

图10是横流速度为9 m/s时沾湿时间段尾部压力图和弹体周围的压力云图,沿直径以横坐标0 mm为射弹尾部中心点,负方向为迎流一侧,正方向为背流侧一端,前方的圆形截面为弹体的尾部。从图中可看出,在1.8 ms之前时,迎流侧尾部压力受横流影响一直变大;1.8 ms时,靠迎流侧尾部压力达到最大,沾湿后,由于水动力影响此时弹体发生偏转,沾湿处压力又呈现出逐渐变小趋势;而背流侧尾部的压力由于射流逐渐消失,呈现逐渐递减的趋势。弹体头部压力较大,可以看出弹体侧面压力从弹体沾湿到弹体发生偏转后,侧面压力先变大后变小。

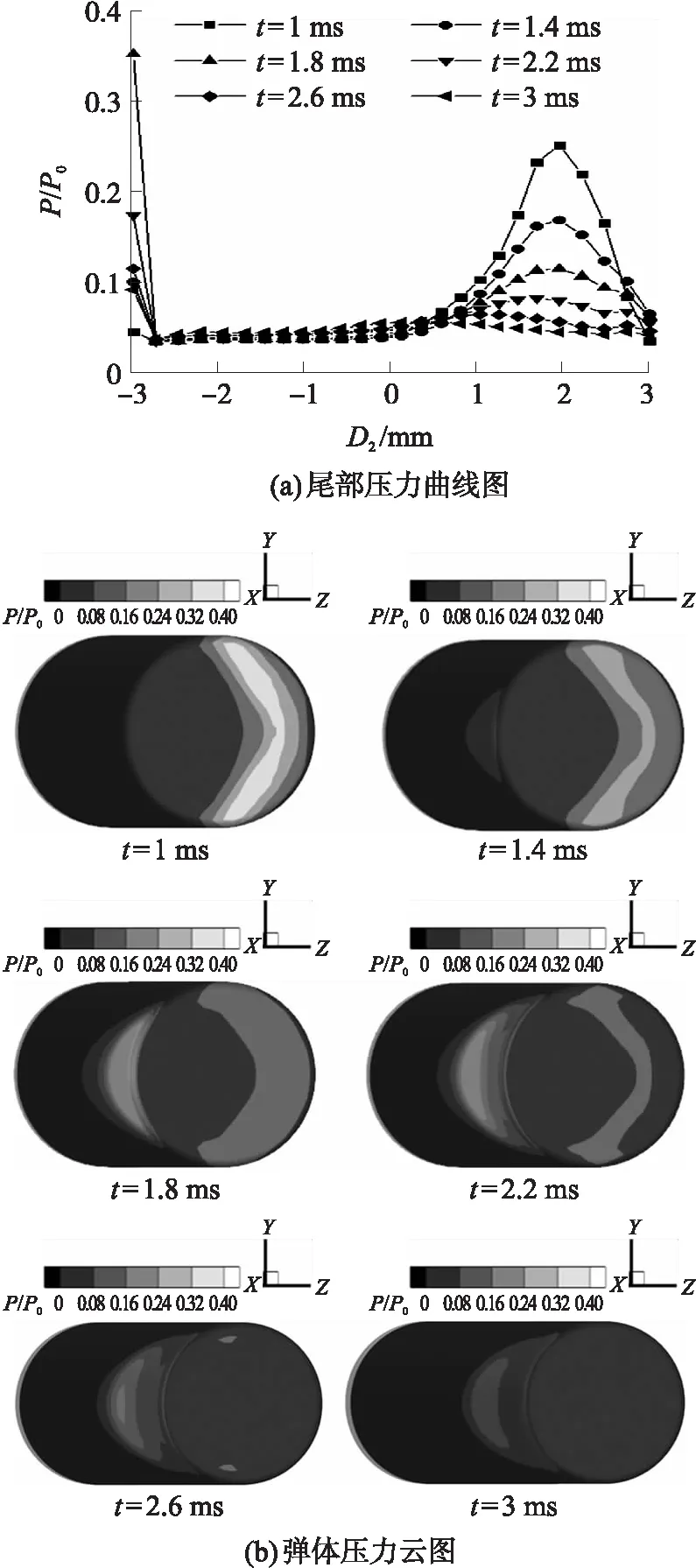
图10 不同时刻下横流速度为9 m/s的压力分布图Fig.10 Pressure distribution for cross-flow velocity of 9 m/s at different moments

图11为t=2.4 ms时不同横流速度下的弹体周围流场速度矢量图。从图中可以看出横流的影响导致弹体壁面附近流体质点背流侧速度远大于迎流侧速度。并且随着横流速度的变大导致弹体尾部产生的高速回流旋涡逐渐消失。

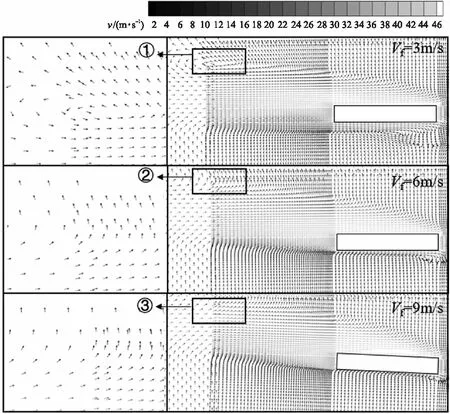
图11 t=2.4 ms不同横流速度下速度矢量图Fig.11 Velocity vector diagram at different cross-flow velocities for t=2.4 ms

3.3 弹体的水动力学特性分析

受横流影响,水下射弹在高速运动时会受到不同的侧向水动力的作用,导致射弹运动速度,运动轨迹情况差异。图12为弹体水下运动示意图,弹体的初始速度方向沿x轴正方向,横流方向沿z轴正方向。图13为射弹在不同横流速度情况下的轴向速度衰减图。从图中可以看出,3种工况下,射弹速度衰减趋势基本相同,横流速度为9 m/s时轴向速度的衰减只稍微略高于横流速度为3 m/s时的工况。这是因为横流速度越大,空泡难以完全包裹住射弹,弹体越早出现尾部大面积沾湿现象,导致射弹前进时所受水的黏性阻力变大,速度下降越快。

图12 弹体水下运动示意图Fig.12 Schematic diagram of the underwater movement of the projectile

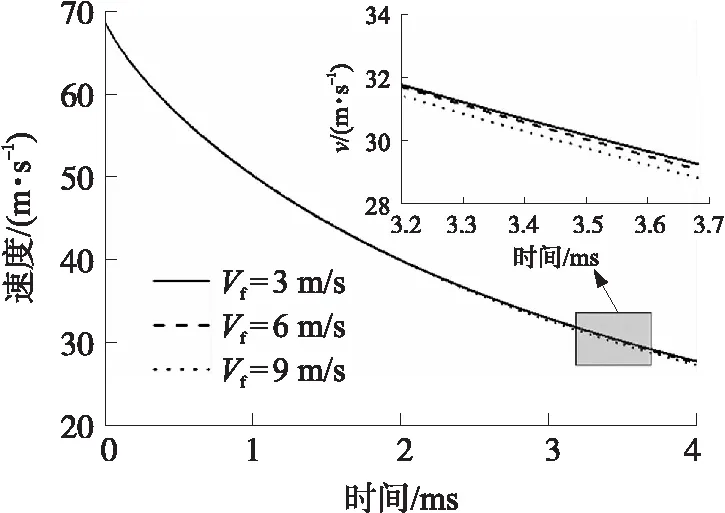
图13 x方向速度衰减曲线图Fig.13 x-direction velocity decay curve

图14为横流速度对弹体x方向阻力系数的影响。从图中可以看出,3种工况下,弹体在运动初始阶段受到的阻力很大;随着空泡的产生,阻力系数逐渐降低。在阻力系数的放大图中可以看到,横流速度对弹体x方向的阻力系数影响较小。

图14 x方向阻力系数图Fig.14 x-direction drag coefficient diagram

图15为横流速度对横流方向侧力系数的影响。射弹水下运动侧向力主要受横流作用的水动力。从图15中可以看出横流速度大,初始阶段弹体的侧力系数越大。随着时间推移,高速弹体表面附近的水发生气化,产生空泡逐渐包裹弹体,空泡内弹体包含大量水蒸气,表面受水动力影响逐渐变小,侧力系数逐渐变小。形成空泡后稳定运动一时间段后,横流速度为9 m/s情况下,弹体表面最先出现沾湿情况,侧力系数逐渐变大,横流速度为6 m/s,3 m/s时,射弹的侧力系数在各自出现沾湿现象时逐渐变大。

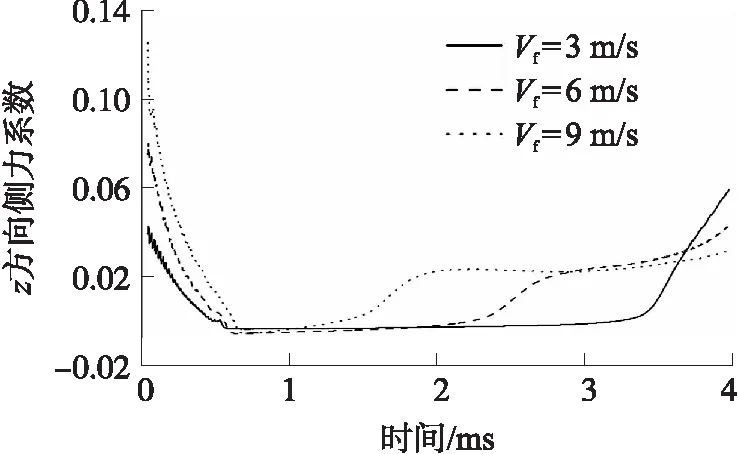
图15 z方向侧力系数图Fig.15 z-direction lateral force coefficient diagram

图16为弹体运动在z方向的偏移量,从图中可以看出横流速度对射弹的运动偏移量影响较大,因为射弹在除了向前运动时会受到的水阻力,同时横流水作用给弹体施加了横向作用力,导致弹体偏移量逐渐变大,并且横流速度大,弹体运动偏移量越大。图17为弹体在z方向的速度曲线图,可以看出在3种工况下,横流速度越大,z方向上速度越大,并且空泡在没有完全包裹住弹体时,弹体受横流水动力持续影响,z方向上速度急剧增大;当随着空泡完全包裹住弹体,弹体在空泡内部受水动力作用变小,z方向上速度呈现缓慢减小的平坦曲线;由于横流作用,尾部在不同时间出现沾湿现象后,水动力作用又变大,3种工况下在不同时间点z方向上速度又逐渐增加,并且横流速度越大,其增大的时间点越早;在t=4.0 ms时,弹体在z方向的偏移速度此时达到横流速度的40%左右。

图16 弹体z方向偏移量曲线图Fig.16 The z-direction offset curve of the projectile body

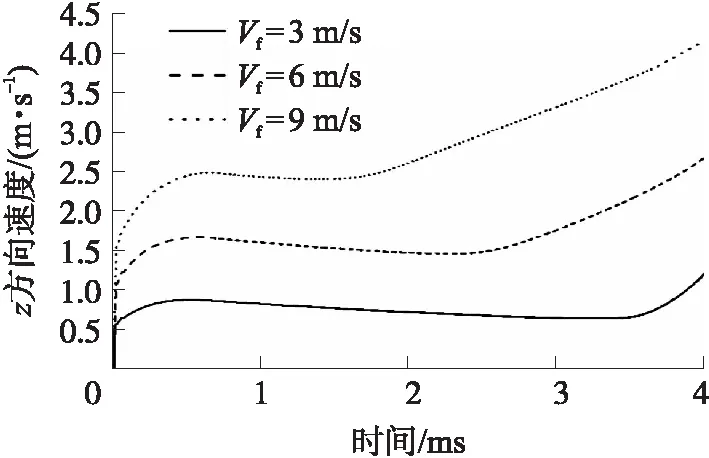
图17 z方向速度变化图Fig.17 z-direction velocity variation graph

图18为射弹偏航角随时间的变化曲线图。随着时间推移,横流作用的持续影响,横流速度越大,偏航角越大,弹体运动轨迹受其影响越大。在初始阶段,弹体头部受横流影响较大,头部先朝负方向(-z)小幅度偏转,持续一段时间后在出现尾部出现沾湿情况后;尾部受横流水作用力后,弹体尾部朝正方向(z)大幅度偏转,横流速度越大,偏航角受横流作用影响越大,偏航角度越大,弹体运动轨道稳定性越差。

弹体在水下沿x方向高速运动,同时受到横流作用,在3种不同工况下,弹体在y方向的位移和绕x、z轴的偏转角都很小。

4 结论

本文在考虑横流情况下对高速射弹水下运动的超空泡流场进行数值模拟,分析了不同横流速度对空泡演变过程、弹体表面压力分布以及弹体的弹道特性的影响,得出的结论如下:

①水下射弹受横流作用影响,射弹产生的空泡不具有对称性。在空泡形成的初始阶段,肩部空泡的迎流测半径小于背流侧,而尾部的迎流测空泡尺寸大于背流侧。

②在相同弹体初始速度和相同时刻条件下,横流速度越大,迎流侧空泡半径越小,背流侧半径越大。在一定的时间点时,会出现弹体尾部的沾湿现象。横流速度越大,出现尾部沾湿的时间越早。

③受横流持续影响,射弹头部压力的最大值从头部中心点逐渐向迎流侧一端移动;横流速度越大,头部的最大压力值越大。

④不同横流速度时,弹体所受到的x方向的阻力系数变化趋势基本相同;因此,随横流速度的改变,弹体在x方向(初始速度方向)的速度衰减趋势基本一致。

⑤射弹在z方向(横流方向)上所受到的侧向力要大于y方向,因此,z方向的偏移量也明显大于y方向。横流速度越大,相同时刻时,弹体的偏移速度也越大;t=4.0 ms时,弹体在z方向的偏移速度达到横流速度的40%左右。