基于物质点法弹丸侵彻靶板的仿真与结构优化
2023-07-03谢桂兰左立来宋慕清肖芳昱
谢桂兰,左立来,宋慕清,肖芳昱,侯 昆
(湘潭大学 机械工程与力学学院,湖南 湘潭 411105)
如何兼顾装甲结构的防护能力和机动灵活性,是现代装甲防护领域重点研究的问题。金属蜂窝夹芯结构由于其本身具有的溃缩吸能和轻质等特性,在现代装甲防护领域备受青睐。
王雪等[1]利用试验和有限元(FEM)数值模拟方法研究了钨合金球侵彻等厚多层板的弹道极限,分析了分层数对靶板弹道极限的影响。徐小刚等[2]采用光滑流体动力学算法(SPH)对蜂窝夹芯板进行了超高速碰撞模拟仿真,研究蜂窝夹芯板的破口尺寸。张延昌等[3]利用有限元软件MSC/Dytran分析了蜂窝夹芯板在横向冲击载荷下的损伤变形,碰撞力和能量吸收等指标,通过与等效平板进行了比较,讨论了结构参数与能量吸收的关系。毕广剑等[4]利用有限元分析软件LS-DYNA对弹丸侵彻2种单层蜂窝夹层结构以及由单层结构相互结合的4种混合双层蜂窝结构进行数值模拟,并对6种结构进行了抗侵彻性能分析,分析了吸能和靶板的结构变形情况。综上所述,发现针对蜂窝结构参数对靶板抗侵彻能力的影响规律的研究文献极少。
物质点法(material point method,MPM)是一种无网格法,避免了拉格朗日法计算大变形问题产生的网格畸变和欧拉法因非线性对流项所产生的数值困难问题[5-6]。因此,物质点法适用于大变形计算,如高速撞击[7-8]、冲击侵彻[9]、爆炸[10]、裂纹扩展[11]、材料失效[12]等问题。本文基于物质点法,模拟了已有文献中弹丸侵彻实心靶板的过程,验证了物质点法在弹丸侵彻靶板问题上的可行性。之后针对弹丸侵彻蜂窝夹芯靶板的侵彻过程进行了模拟计算。研究了不同胞元壁厚、不同厚度蜂窝板的蜂窝夹芯靶板对弹丸的抗侵彻规律,丰富了弹丸侵彻靶板问题的研究方法。
1 理论基础
使用物质点法求解弹丸侵彻靶板问题时,采用拉格朗日法描述离散质点,用欧拉法描述背景网格。离散质点携带物体所有材料和运动信息,在每个时间步,将信息映射到背景网格进行求解,计算结束后相关信息被重新映射回离散质点进行更新。在下个计算时间步中,更新背景网格用于后续计算,因此避免了使用有网格法模拟大变形问题时产生的网格畸变缺陷。此外,质点和背景网格之间具有无相对运动的优点,有效避免了因非线性对流项造成的求解困难等问题[6]。
1.1 虚功方程
弹丸与靶板接触并发生穿透时,需要同时遵循质量、动量与能量守恒规律,即必须符合下列控制方程:
初始条件:
vi(X,0)=v0i(X),ui(X,0)=u0i(X)
(1)
本构关系:
(2)
几何方程:
(3)
质量守恒方程:
(4)
动量守恒方程:
(5)
能量方程:
(6)
边界条件:
(7)
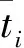
1.2 显式物质点法更新
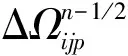
(8)
(9)
式中:NIp为结点I的形函数在质点p处的值,n为迭代步数。
计算得质点密度为
(10)
(11)
(12)
(13)
对动量方程进行积分求解:
(14)
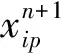
2 物质点法程序验证
为了验证物质点法在模拟弹丸侵彻靶板问题上的可行性,根据第1节介绍的物质点法基本理论,使用FORTRAN语言编写弹丸侵彻靶板过程的物质点法程序,选取文献[1]中的几何模型参数和材料模型参数进行数值模拟。
弹丸侵彻靶板的几何模型如图1所示,弹丸为实心球形,材料为钨合金,直径D为9.45 mm,质量为8.05 g;靶板为7.2 mm(2.4 mm+2.4 mm+2.4 mm)厚Q235钢板。
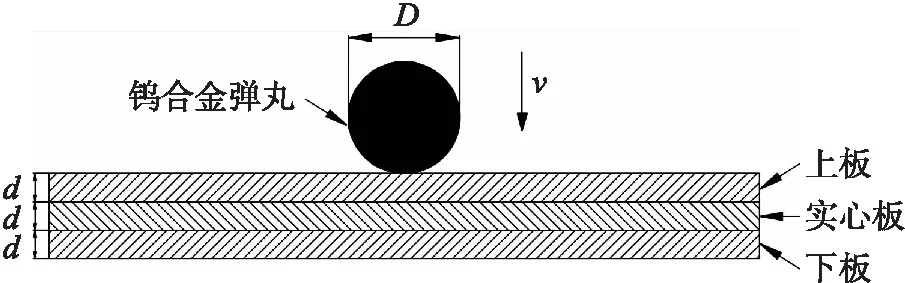
图1 几何模型Fig.1 Geometric model
钨合金弹丸和靶板间距为0时的物质点法离散模型如图2所示。弹丸的质点间距为0.15 mm,靶板的质点间距为0.2 mm,背景网格为六面体网格,网格间距为1 mm,整个模型共离散为3 377 376个质点。由于钨合金具有明显的应变率特征[13],因此弹丸选用PLASTIC材料模型。钨合金弹丸材料模型参数如表1所示,其中ρ为材料密度,E为杨氏模量,μ为泊松比,σ为屈服应力,Et为切线模量,nY为硬化参数指标,F为失效应变。Johnson-Cook模型经过大量理论和试验论证,被证明适用于描述爆炸和超高速碰撞等涉及高应变率问题的材料响应情况,靶板在弹丸侵彻作用下属于大变形问题,因此对靶板采用Johnson-Cook模型。靶板材料模型参数如表2所示,其中G为剪切弹性模量,A、B、c、m、nb均为材料常数,Tm为材料熔点,Tr为室温,D1~D5为材料损伤模型常数。状态方程是为了描述材料压力、体积应变和内能之间的关系。结合统计学和热力学理论得到材料在冲击载荷下的Mie-Grüneisen状态方程,可以很好地描述靶板在弹丸冲击载荷作用下的热力学行为。因此,在弹丸侵彻靶板的模拟过程中,采用Mie-Grüneisen状态方程来进行对靶板进行描述,状态方程参数如表3所示。表中,s为von Mises等效应力,γ0为Grüneisen常数,c0为声速,cp为等容比热容,靶板四周为固定约束,其余面为自由约束,求解格式为USF格式,时间步长因子取0.9。

表1 钨合金弹丸的材料模型参数Table 1 Material parameters of tungsten alloy projectile

表2 Q235钢靶板的材料模型参数Table 2 Material parameters of Q235 steel target

表3 Q235钢靶板Mie-Grüneisen状态方程参数Table 3 Q235 Steel target state parameters of Mie-Grüneisen equation

图2 物质点法离散模型Fig.2 Discrete model of the material point method
文献[1]中使用有限元法模拟弹丸侵彻7.2 mm厚靶板得到的弹道极限速度范围为526~531 m/s。通过编写的物质点法程序得到的弹丸侵彻靶板的仿真模型,对弹丸侵彻靶板的过程进行模拟仿真,得出弹丸侵彻靶板的弹道极限速度范围,结果如图3所示,图中v0为弹丸初始速度、v1为剩余速度。由图可知使用物质点法进行弹丸侵彻7.2 mm厚靶板得到的弹道极限速度范围在526~537 m/s,其值与有限元结果仅相差1.1%。使用物质点法模拟得到的弹丸侵彻靶板的弹道极限速度范围从数值和靶板破坏形状上都与有限元模拟结果极其吻合。
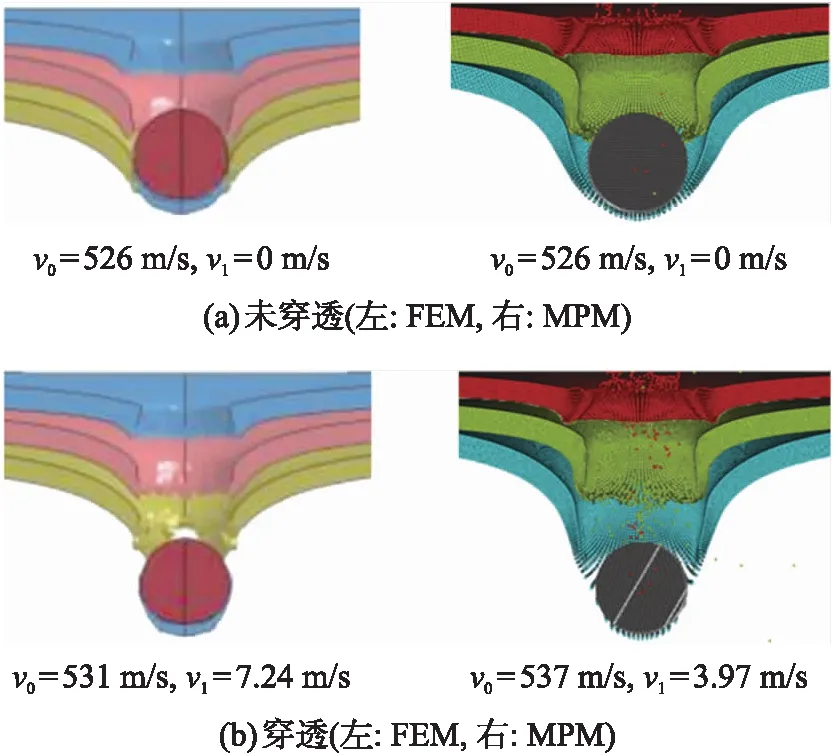
图3 物质点法的弹道极限速度与文献[1]对比Fig.3 Comparison of ballistic limit velocity between the material point method and Ref. [1]
再根据文献[1]中的弹丸初始速度,通过物质点法模拟不同初始速度的弹丸侵彻靶板的过程。得到的弹丸穿透靶板的剩余速度如表4所示。
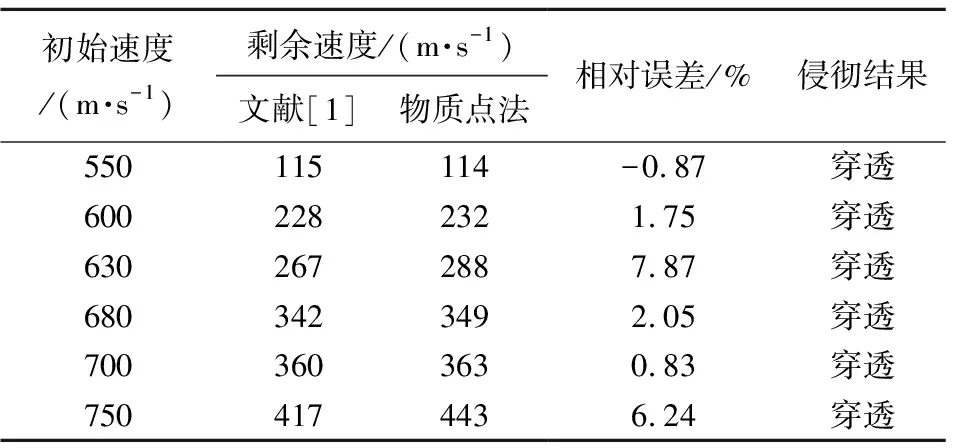
表4 弹丸侵彻靶板的仿真结果对比Table 4 Comparison of simulation results of projectile penetration target plate
通过表4可知,在不同初始速度下物质点法和有限元法模拟的弹丸剩余速度的变化规律一致,且最大误差小于8%。说明物质点法能够较好地模拟弹丸侵彻靶板时的弹丸撞击靶板和靶板破损变形的过程,使用物质点法在弹丸侵彻靶板问题上是有效可行的。
3 靶板结构设计优化及仿真
3.1 弹丸侵彻蜂窝夹芯靶板计算模型
在靶板质量恒定的前提下,为了提高靶板的抗侵彻能力,将靶板中间层实心板替换为相同材料的蜂窝板。正六边形蜂窝胞元结构示意图如图4所示,其中hhc为水平胞壁长度,l为胞元斜壁长度,在正六边形蜂窝结构中hhc=l,Dhc为蜂窝结构胞元孔径,δhc为蜂窝胞元壁厚,α为胞元内角,正六边形蜂窝结构的胞元内角为30°。当取蜂窝结构胞元壁厚δhc为0.4 mm,蜂窝结构胞元孔径Dhc为6 mm,蜂窝板总厚度T为3.5Dhc时,取蜂窝板的质点间距与实心板的质点间距均为0.2 mm,在物质点法离散模型中实心板被离散为1 080 000个质点,蜂窝板被离散为1 072 800个质点,相差为0.67%,由于物质点法是将物体离散为一系列离散质点,质点携带物体的质量信息,所以蜂窝板的质量与实心板的质量近似相同。
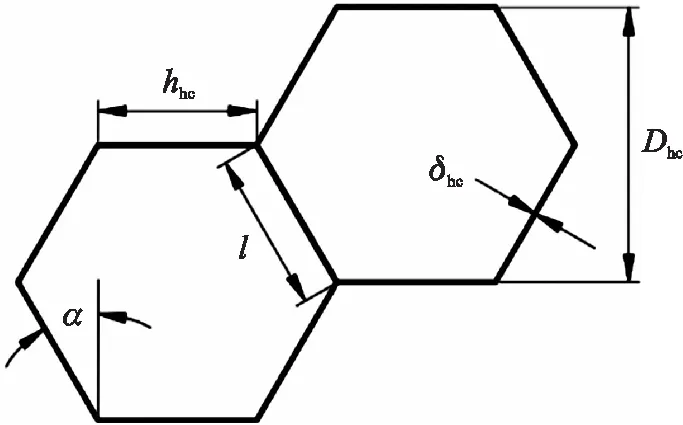
图4 蜂窝胞元示意图Fig.4 Schematic diagram of cellular cells
弹丸侵彻蜂窝夹芯靶板的几何模型如图5所示,弹丸为实心球形,材料为钨合金,直径为9.45 mm,质量为8.05 g;蜂窝夹芯靶板材料为Q235钢,上板和下板厚度均为2.4 mm。使用物质点法建立的弹丸侵彻蜂窝夹芯靶板的离散模型如图6所示,弹丸的质点间距为0.15 mm,靶板的质点间距为0.2 mm,背景网格采用六面体网格,网格间距为1 mm,整个仿真模型被离散为3 370 176个质点。钨合金弹丸和蜂窝夹芯靶板的材料参数见表1~表3。
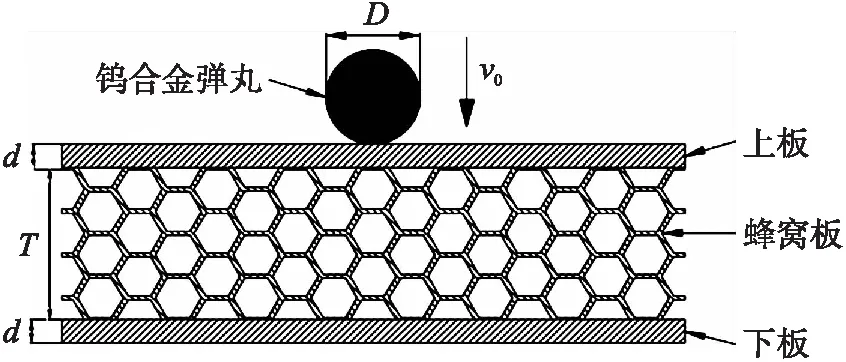
图5 几何模型Fig.5 Geometric modeling
图6 物质点法离散模型Fig.6 Discrete model of the material point method
由图7可知,弹丸在初始速度606 m/s时未能穿透蜂窝夹芯靶板,而在初始速度610 m/s时穿透了蜂窝夹芯靶板,即使用物质点法模拟得到的弹丸侵彻蜂窝夹芯靶板的弹道极限速度范围在606~610 m/s。相比文献[1]中弹丸侵彻实心靶板的弹道极限速度范围(526~537 m/s),其值明显提高,说明蜂窝夹芯靶板的抗侵彻能力相比实心靶板显著提高。
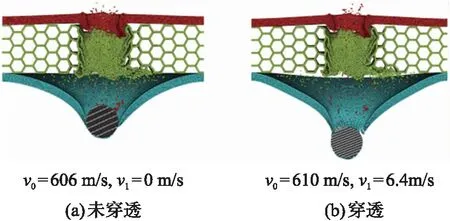
图7 弹丸侵彻蜂窝夹芯板的弹道极限速度Fig.7 Ballistic limit speed of projectile penetration into honeycomb sandwich panel
再根据弹丸侵彻图1所示实心靶板的一系列初始速度,选取相同的初始速度,来进行弹丸侵彻蜂窝夹芯靶板的仿真,对比物质点法和有限元法得到的弹丸剩余速度,结果如表5所示。可知,弹丸侵彻蜂窝夹芯靶板后的剩余速度相比侵彻实心靶板有较大幅度的下降,降低比例在20.09%~37.10%之间,且在速度较低时(550 m/s和600 m/s),弹丸并未穿透蜂窝夹芯靶板。这说明蜂窝结构夹芯板对弹丸的速度降低效果更显著,能较大程度地提高靶板的抗侵彻性能。
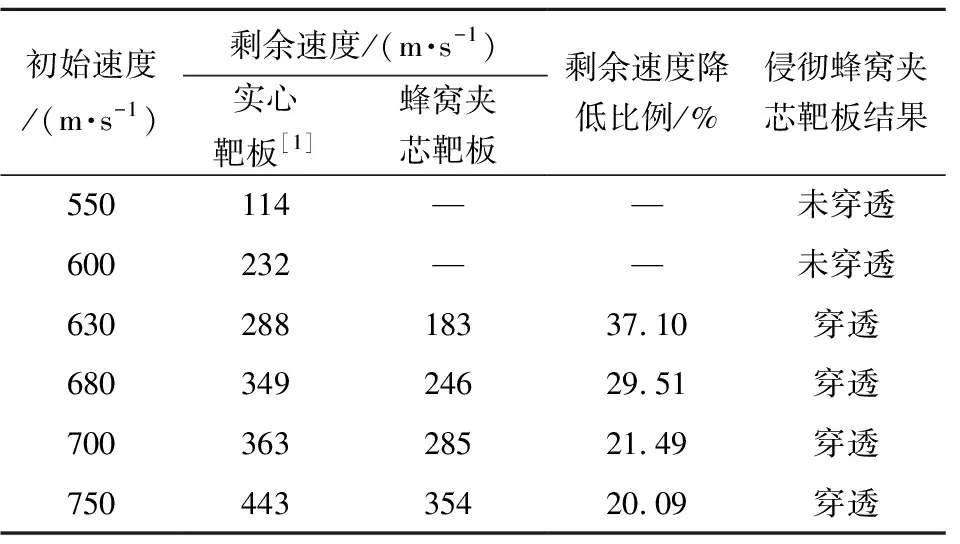
表5 弹丸侵彻蜂窝夹芯板的仿真结果Table 5 Simulation results of projectile penetration into honeycomb sandwich panels
利用物质点法模拟得到的弹丸侵彻实心靶板和蜂窝夹芯靶板的弹道极限速度,结合弹丸速度时程曲线,可得到靶板各层的吸能情况及占整个靶板吸收能量的比例。靶板吸收能量的能力经常用能量吸收率来表示,实心靶板和蜂窝夹芯靶板各层的能量吸收率情况见表6。
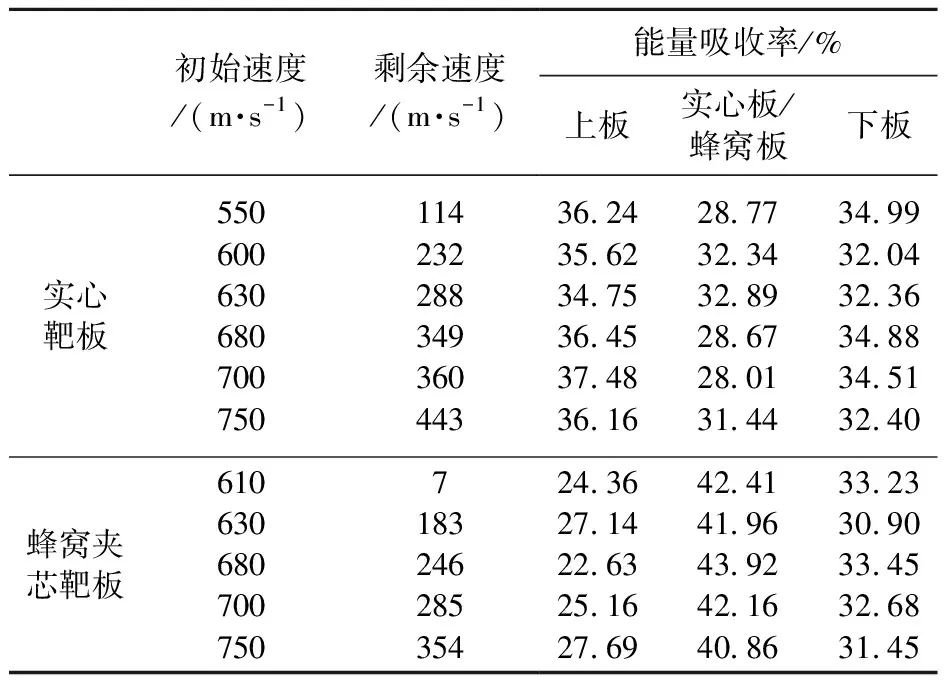
表6 靶板各层的能量吸收率情况Table 6 Energy absorption rate of each layer of the target plate
由表6可知,蜂窝夹芯靶板中蜂窝板的能量吸收率相比于中间层实心板的吸收能量明显提高,中间层的吸能率从28.01%~32.89%提升到40.86%~43.92%,说明蜂窝结构溃缩吸能性能较好,起到了更好的缓冲吸能效果,能提高靶板的抗侵彻能力。
3.2 蜂窝夹芯靶板结构参数对靶板抗侵彻能力的影响分析
3.2.1 蜂窝板厚度的影响
为了探究蜂窝板厚度对蜂窝夹芯靶板抗侵彻能力的影响,通过编写的物质点法程序,分别对弹丸侵彻不同厚度蜂窝板的蜂窝夹芯靶板进行数值模拟。以相同的弹丸初始速度(680 m/s)侵彻靶板,获得弹丸侵彻不同厚度蜂窝板的蜂窝夹芯靶板的剩余速度,弹丸的剩余速度时程曲线如图8所示,剩余速度与蜂窝板厚度之间的关系如图9所示。
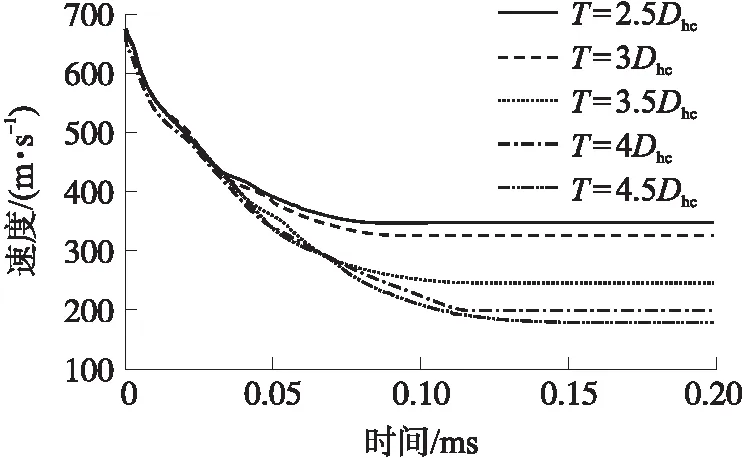
图8 弹丸侵彻不同厚度蜂窝夹芯板速度时程曲线Fig.8 Projectiles penetrate honeycombs of different thicknesses Sandwich panel speed time history curve
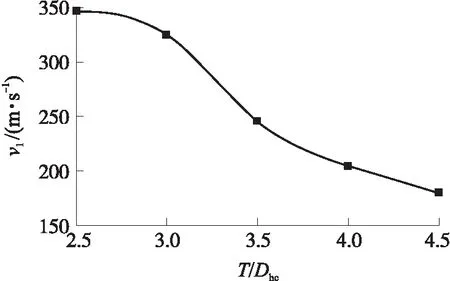
图9 弹丸剩余速度与蜂窝板厚度的关系曲线Fig.9 Curve of the residual velocity of the projectile and the thickness of the honeycomb plate
可知,随着蜂窝板厚度的增加,弹丸剩余速度不断下降。在蜂窝板厚度较小时,随着厚度的增加,弹丸剩余速度虽有所下降,但下降幅度较为平缓。之后再随着蜂窝结构芯层厚度的增加,弹丸剩余速度下降程度先急剧增大后趋于平缓。这说明蜂窝夹芯靶板的抗侵彻能力先急剧上升,后随着蜂窝板厚度的增加而趋于平缓,此时蜂窝板厚度的增加对降低弹丸速度的作用开始降低,再继续增加蜂窝板的厚度不能再有效降低弹丸速度。
将弹丸剩余速度与蜂窝板厚度的关系曲线进行微分处理,获得剩余速度曲线斜率k1,其与蜂窝板厚度的曲线如图10所示。

图10 弹丸剩余速度曲线斜率与蜂窝板厚度的关系曲线Fig.10 Curve of the slope of the projectile remaining velocity curve and the thickness of the honeycomb plate
可知,斜率的大小表示弹丸剩余速度曲线的衰减速度。在斜率极值处之前,斜率的绝对值持续增大,说明这期间随着蜂窝板厚度的增加,蜂窝夹芯靶板对弹丸速度的降低效果急剧上升;在斜率极值处之后,斜率的绝对值在减小,此时再随着蜂窝板厚度的增加,蜂窝夹芯靶板对弹丸速度的降低作用已经慢慢趋于平缓。蜂窝夹芯靶板在斜率曲线的极值(T=3.5Dhc附近)处具有抗侵彻和轻质的最优解。
3.2.2 蜂窝胞元壁厚的影响
为了探究蜂窝胞元壁厚对蜂窝夹芯靶板抗侵彻能力的影响作用,通过编写的物质点法程序,对弹丸侵彻不同壁厚蜂窝夹芯板进行数值模拟。以相同弹丸初始速度(680 m/s)侵彻靶板,获得弹丸侵彻不同蜂窝胞元壁厚的蜂窝夹芯靶板的剩余速度。得到弹丸剩余速度的时程曲线如图11所示。
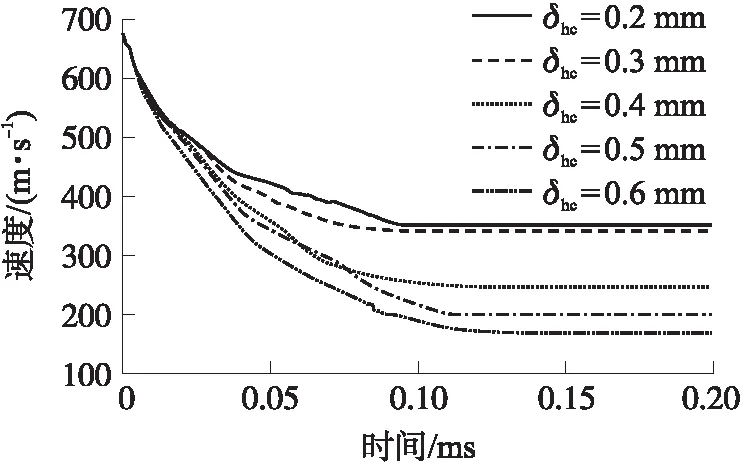
图11 弹丸侵彻不同壁厚蜂窝夹芯板速度时程曲线Fig.11 Velocity and time history curve of projectile penetration through honeycomb sandwich panels with different wall thicknesses
图12所示为弹丸侵彻不同胞元壁厚的蜂窝夹芯靶板的剩余速度与蜂窝胞元壁厚之间关系图。可知,随着蜂窝胞元壁厚的增加,弹丸剩余速度不断下降。在胞元壁厚较小时,随着壁厚的增大,弹丸剩余速度下降幅度较为平缓。之后再随着蜂窝胞元壁厚的增大,弹丸剩余速度下降程度先急剧增大后趋于平缓,说明蜂窝夹芯靶板的抗侵彻能力先急剧上升,后随着蜂窝胞元壁厚的增加而趋于平缓,说明此时蜂窝胞元壁厚的增加对降低弹丸速度的作用开始降低,此时再继续增加蜂窝胞元壁厚对弹丸速度的影响减小。
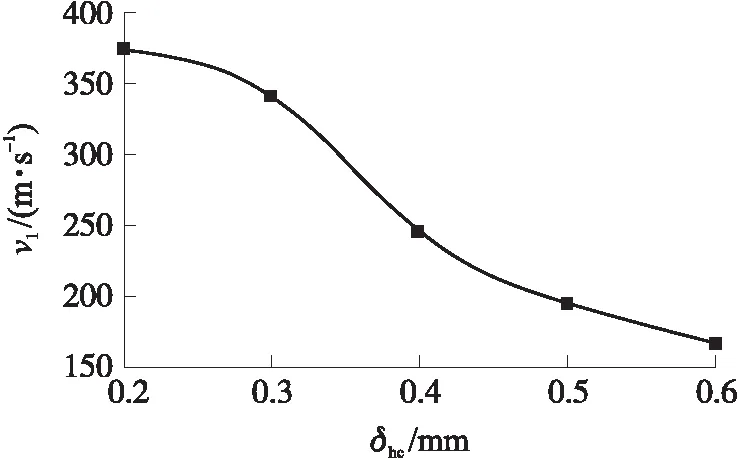
图12 剩余速度与蜂窝胞元壁厚的关系Fig.12 Relationship between residual velocity and cell wall thickness
将弹丸剩余速度与蜂窝胞元壁厚的关系曲线进行微分处理,获得弹丸剩余速度曲线斜率k2与蜂窝胞元壁厚的曲线关系如图13所示。可知,随着蜂窝胞元壁厚的增加,蜂窝夹芯靶板对弹丸速度的降低效果先急剧上升,在斜率极值处之后,斜率的绝对值在减小,此时再随着蜂窝胞元壁厚的增加,蜂窝夹芯靶板对弹丸速度的降低作用已经慢慢趋于平缓。因此蜂窝夹芯靶板在斜率曲线的极值处(δhc=0.4 mm)具有抗侵彻和轻质的最优解。
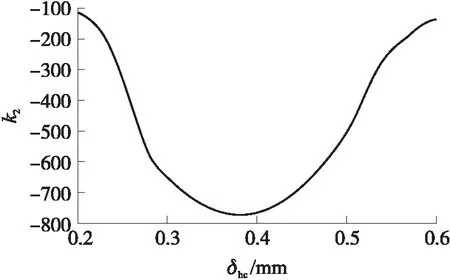
图13 剩余速度曲线斜率与蜂窝胞元壁厚关系Fig.13 Relationship between the slope of the remaining velocity curve and the wall thickness of the cellular cell
4 结束语
本文通过物质点法对弹丸侵彻靶板的过程进行了模拟与验证,设计了三层蜂窝夹芯靶板,分析了蜂窝芯厚度及胞元壁厚对蜂窝夹芯板抗侵彻能力的影响规律,得出以下结论:
①钨合金弹丸侵彻三层靶板的弹道极限速度约为526~537 m/s,在靶板总质量不变的情况下,蜂窝夹芯靶板的弹道极限速度提高到606~610 m/s,说明优化后的蜂窝夹芯靶板的抗侵彻能力优于等质量的实心靶板。
②通过对蜂窝板厚度和蜂窝胞元壁厚两个试验参数进行仿真分析,在相同初始速度下,得到不同试验参数下的弹丸穿出速度,结合剩余速度与试验参数曲线和剩余速度斜率微分曲线,得到靶板在斜率微分曲线极值处的防护和轻质的最优解。
③证明物质点法在解决弹丸侵彻靶板问题上是有效可行的,可为相关研究提供数值模拟,也可为装甲防护设计提供参考。
