二元信息挖掘多模型融合异常弹着靶速度预测

田 珂

(中国人民解放军63861部队,吉林 白城 137001)

常规靶场试验中,着靶速度是影响立靶密集度计算的重要因素[1-2]。弹丸着靶速度通常利用连续波雷达测得,可以近似为弹丸撞击目标靶瞬间时刻雷达测得的弹丸径向速度[3]。具体试验中,受到天气、火炮工况和雷达故障等影响,会出现无法准确测得弹丸的着靶速度的情况。数据的缺失或误差会严重影响对弹丸和火炮战斗性能的准确鉴定,因此选择利用已测数据,预测出需要重构的着靶速度,补全试验数据成为一项必要的工作。

文献[4-5]通过提取弹丸着靶时刻的图像,进而预测出缺失的着靶速度,主要是把初速雷达和连续波雷达的数据进行融合,利用初速雷达的某段数据预测出连续波雷达的着靶速度。但如果弹丸着靶之前飞行状态出现异常,该方法将会出现预测错误。为此利用弹丸着靶前后的图像信息和数字信息建立预测模型,挖掘出着靶前后的图像特征和数字特征,可以有效提高异常弹丸着靶速度预测精度。

随着机器学习研究的不断进步,为基于图像和数字信息的着靶速度预测方法研究提供了新的思路[6]。支持向量机(SVM)在数据量不是特别大的情况下,具有速度快、精度高以及鲁棒性强等优势。支持向量回归机(SVR)是支持向量机在回归领域的应用,具有较强的学习功能和特征,对小样本数据具有较好的适应性,其相关研究和应用涉及图像识别和分类[7-11]。但是核函数参数和正则化参数是影响支持向量机预测精度的两大因素,所以选择利用遗传算法(GA)搜寻出最佳的核函数参数和正则化参数,建立遗传算法优化最小二乘支持向量机模型(GA-LSSVM)以提高预测精度。实验结果表明,经过多模型融合,遗传算法优化LSSVM预测着靶速度误差最小,等于0.028%,远小于1‰,达到了国军标关于连续波雷达测试弹丸着靶速度的误差要求[2],表明该方法针对异常弹丸,能发挥出较强的预测能力,可以作为异常弹丸着靶速度预测模型

1 二元信息挖掘

1.1 图像信息挖掘

弹丸着靶前后的图像特征提取是指挖掘出弹丸着靶时刻瀑布图中的图像特征,主要包括颜色、纹理、形状和空间关系特征等。与几何特征相比,颜色特征更为稳健,对于物体的大小和方向均不敏感,表现出较强的鲁棒性[12]。由于不同弹丸着靶时刻的瀑布图中速度分布不同,导致信噪比有所区别,因此颜色特征是体现不同瀑布图差异的一个重要特征。处理颜色特征可通过颜色矩方法处理[13],这是因为图像中任何颜色的分布均可以用它的矩表示。根据概率论的理论,随机变量的概率分布可以由其各阶矩唯一地表示和描述。不同弹丸着靶时刻瀑布图中数据点的分布不同,所以瀑布图的色彩分布也可以认为是一种概率分布。因此瀑布图的特征可以由其各阶矩来表示。颜色矩通常用一、二、三阶矩表示,一阶颜色矩采用一阶原点矩表示,反映的是图像整体的明暗程度,计算公式如式(1)所示;二阶颜色矩采用的是二阶中心矩的平方根,反映的是图像颜色的分布范围,计算公式如式(2)所示;三阶颜色矩采用的是三阶中心矩的立方根,反映了图像颜色分布的对称性,计算公式如式(3)所示。

(1)

(2)

(3)

式中:Ei为第i个颜色通道的一阶颜色矩阵,对于RGB颜色特征的图像,i=1,2,3;pij是第j个像素的第i个颜色通道的颜色值;si为第i个颜色通道的二阶颜色矩阵;ti是在第i个颜色通道的三阶颜色矩阵;N为数据个数。

1.2 数字信息挖掘

数据特征挖掘是指从雷达测试的弹丸在着靶前后众多径向速度中,准确挖掘出关键的数据特征,然后利用其预测出缺失的着靶速度。由于不同弹丸着靶时刻的瀑布图中数据点的分布不同,而着靶时刻之前的数据点可以认为是起因,着靶之后的数据点的分布可以认为是结果,两者对应的径向速度都与着靶时刻的径向速度存在内在的关联性,所以选择从径向速度突然发生变化前第3个点开始,往后连续计算出10个点的径向速度,然后把这10个点的径向速度作为输入向量,对应的着靶速度作为输出向量,利用已测数据建立支持向量回归机模型,然后把未能准确测试的着靶速度瀑布图对应的10个径向速度代入到所建模型就能预测出对应的着靶速度。该方法合理地避开了必须是正常弹丸的限制,扩展到了对异常弹丸的有效包容。

试验现场连续波雷达布站示意图如图1所示。火炮射角通常是1°左右,炮口距离目标靶的距离通常为1 km。连续波雷达通常布站在火炮左后方,雷达天线面中心点距离火炮耳轴的纵向垂直距离是30 m左右,距离火炮耳轴的横向垂直距离通常是5 m左右。雷达测试运动目标径向速度原理如图2所示。同一个试验任务射击的所有弹丸,使用的是同一块目标靶,保证了试验数据的前后一致性和相关性。

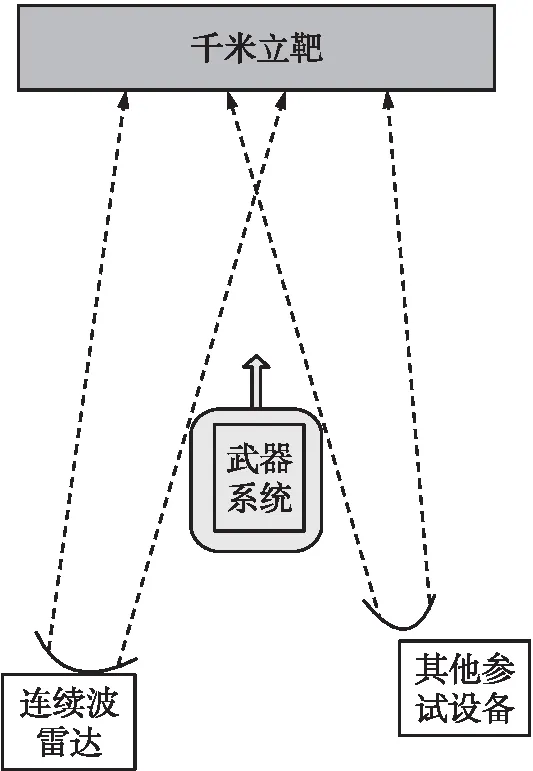
图1 雷达布站示意图Fig.1 Schematic diagram of radar station layout

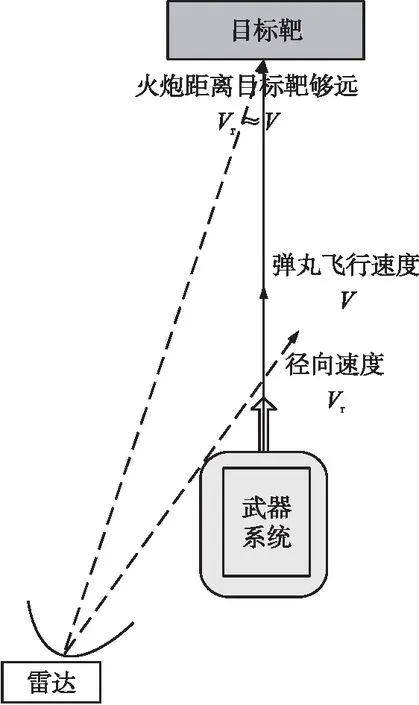
图2 雷达测试弹丸速度示意图Fig.2 Schematic diagram of radar test projectile velocity

2 多模型融合原理

2.1 支持向量回归机建模原理

支持向量回归机是用于解决回归问题的支持向量机模型,它是支持向量机在回归估计问题中扩展和应用[14]。支持向量回归机的目标函数是找到一个让所有点都逼近的最优超平面。其回归机的回归函数如式(4)所示:

(4)

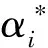
2.2 GM(1,1)灰色模型建模原理

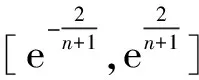
表1 GM(1,1)预测结果评价表Table1 Evaluation table of GM(1,1)prediction results

(5)

(6)

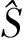
2.3 遗传算法优化LSSVM建模原理

2.3.1 最小二乘支持向量机

最小二乘支持向量机(LSSVM)是为了便于求解而对支持向量机(SVM)的一种改进。与标准支持向量机相比,最小二乘支持向量机用等式约束代替支持向量机中的不等式约束,避免了求解耗时的二次规划问题,加快了求解速度[16]。

2.3.2 遗传算法优化LSSVM参数

利用遗传算法优化支持向量机参数主要是优化sigma和gama两个参数,sigma是RBF径向基核函数的参数,表示在更高维特征空间中数据点分布的离散程度;而gama主要是在最小二乘支持向量机模型中的回归函数两项中起到平衡调节的作用。具体优化步骤如图3所示[17]。

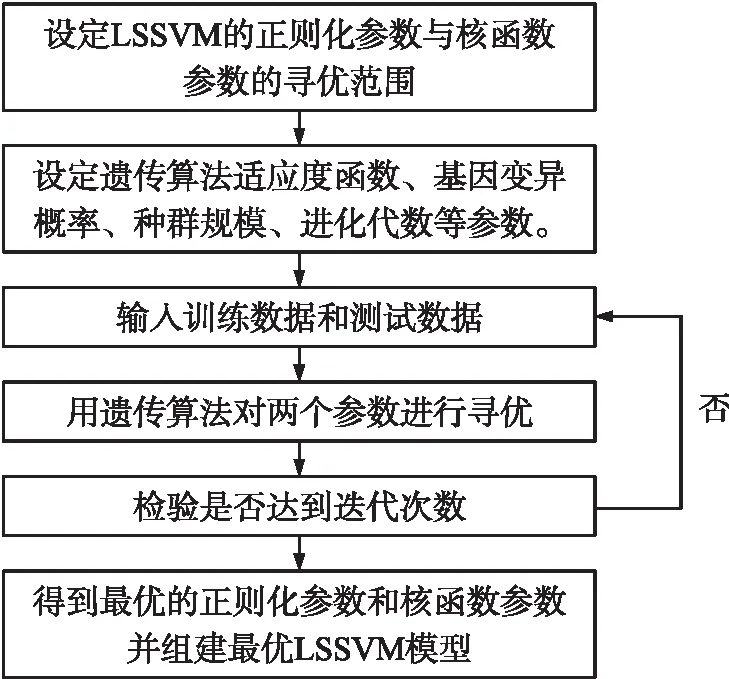
图3 遗传算法搜寻LSSVM最佳参数过程Fig.3 Genetic algorithm searching for the best parameters of LSSVM

2.3.3 多模型融合

多模型融合的主要步骤如下:

①先把颜色特征矩阵作为特征向量,着靶速度实测值作为目标向量,构建样本矩阵。对该样本矩阵进行归一化处理,消除量纲带来的差异。然后把归一化后的样本矩阵的80%作为训练数据,20%作为测试数据,进而建立特征向量与目标向量的支持向量回归机模型,经过建模预测就可以得到支持向量回归机对训练数据中着靶速度的拟合值,以及对测试数据中着靶速度的预测值。

②把数字信息作为特征向量,对应着靶速度实测值作为目标向量,构建另一样本矩阵。采用同样的归一化方法消除该样本矩阵量纲带来的差异。然后把该归一化后的样本矩阵划分为训练数据和测试数据,训练数据占据80%的比例,测试数据占据20%的比例,进而建立特征向量与目标向量的支持向量回归机模型。经过建模预测得到训练数据中着靶速度的拟合值,以及对测试数据中着靶速度的预测值。

③第一步和第二步采用同样的方法将着靶速度实测值划分成了训练数据和测试数据。利用训练数据建立GM(1,1)灰色模型,可以得到该灰色模型对训练数据的拟合值。然后对测试数据进行预测,就得到了该灰色模型预测出的着靶速度。

④利用三个模型对训练数据的拟合值建立遗传算法优化LSSVM模型,然后再把三个模型对测试数据的预测值带入遗传算法优化LSSVM模型,得到该模型预测出的着靶速度。

该方法将支持向量回归机、GM(1,1)和遗传算法优化LSSVM有效融合到了一起,建立多模型融合方法,既包含了图像信息也包含了数字信息;既挖掘出了着靶速度的非线性特征,也挖掘出了线性特征,把所有模型的预测能力组合到了一起,克服了单一模型预测能力的不足[18-19]。

3 实验验证

选取连续波雷达测得的某型坦克炮38发着靶速度进行算例分析,38发弹丸由同一个试验利用同一个目标测得,所有数据具有前后一致性和相关性。38发着靶速度变化曲线如图4所示,可以看出,着靶速度基本上围绕一个固定值上下浮动,同时具有逐渐增大的趋势,整体上既具备线性变化特征,又具备非线性变化特征,而且非线性特征强于线性特征,因此应当同时建立线性模型和非线性模型一同预测。线性变化规律选择采用GM(1,1)灰色模型建模预测,非线性变化规律选择采用支持向量回归机建模预测。

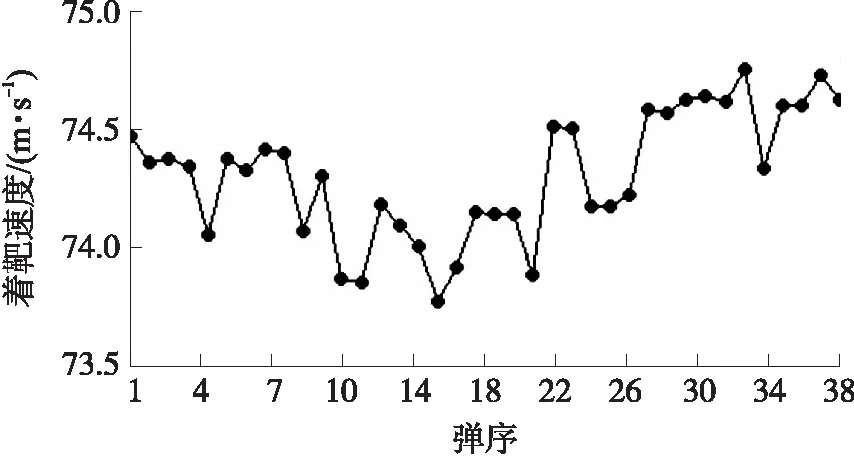
图4 着靶速度测量值Fig.4 Tested impact velocity

3.1 图像提取验证分析

按照相同的尺寸和像素利用雷达终端提取出38发弹丸着靶时刻的瀑布图。按照式(1)～式(3)计算出的38张瀑布图对应的颜色矩,结果如表2所示。

表2 瀑布图对应的R、G、B颜色通道的颜色矩Table 2 Color moments of R,G and B color channels corresponding to waterfall diagrams

建立支持向量回归机之前,将表1中80%数据作为训练样本,20%数据作为测试样本,即把第1～30发作为训练数据,第31～38发作为测试数据[20]。首先对样本数据进行归一化处理,以消除量纲之间的差异[21]:

(8)

式中:xmin为数据的最小值,xmax为数据的最大值。

由于支持向量回归机预测精度容易受到核函数的影响,为了确定出最佳核函数以建立最佳模型,对比了不同的核函数下支持向量回归机预测值,结果如图5所示。由图可知,线性核函数拟合值与训练数据的平均相对误差为0.217%;径向基核函数拟合值与训练数据的平均相对误差为0.211%,sigmoid核函数拟合值与训练数据的平均相对误差为0.274%;多项式核函数拟合值与训练数据的平均相对误差为0.213%。最终确定利用图像信息分析时,选用径向基核函数建立支持向量回归机对第31～38发着靶速度进行预测,结果如表3所示。预测值与实测值的平均相对误差为0.647%,说明图像提取的方法可行性。

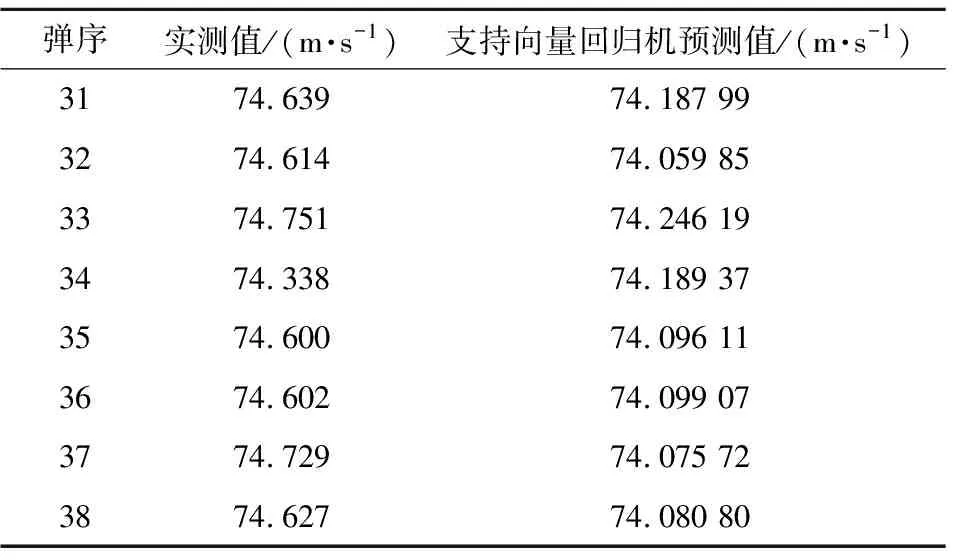
表3 基于图像提取的着靶速度预测值对比Table 3 Comparison of predicted impact velocity based on image information with measured value

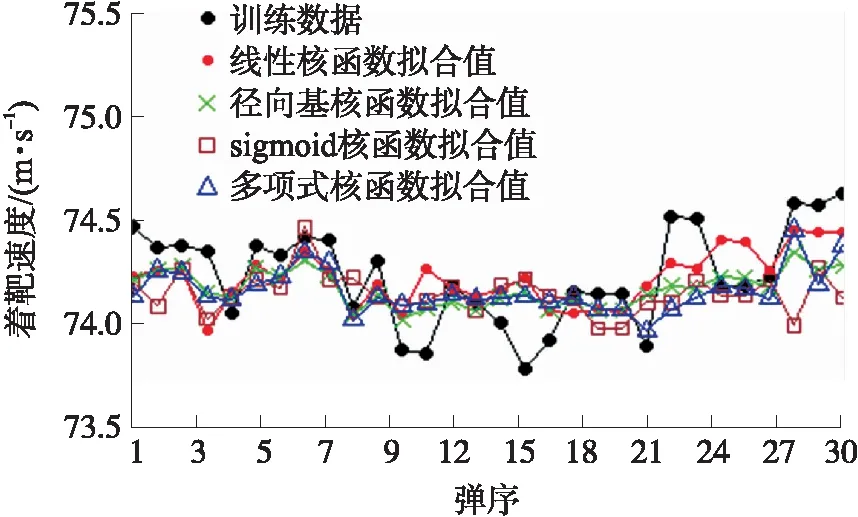
图5 颜色矩阵训练的支持向量回归机不同核函数拟合曲线Fig.5 Color matrix trained support vector regression machine fitting curves with different kernel functions

3.2 数字挖掘验证分析

按照上文方法,针对所有测试弹丸的径向速度进行挖掘,结果如图6所示。将每条曲线的10个径向速度作为特征向量,对应的着靶速度作为目标向量,同样把第1～30发作为训练数据,第31～38发作为测试数据,建立支持向量回归机模型。不同核函数下支持向量回归机拟合训练数据的关系曲线如图7所示,经过分析对比得出线性核函数建立的支持向量回归机拟合值与训练数据的平均相对误差为0.097%;径向基核函数建立的支持向量回归机拟合值与训练数据的平均相对误差误差0.1%;sigmoid核函数建立的支持向量回归机拟合值与训练数据的平均相对误差误差0.177%;多项式核函数建立的支持向量回归机与训练数据的平均相对误差0.141%。所以线性核函数建立的支持向量回归机拟合训练数据的精度最高,是建立支持向量回归机最佳核函数。

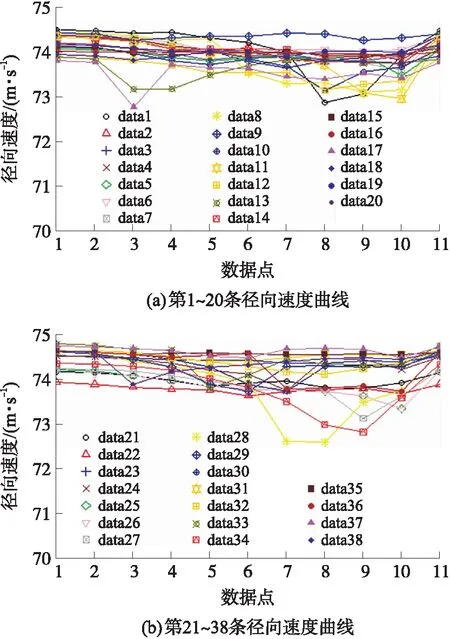
图6 测试弹丸的径向速度Fig.6 Radial velocitis of the tested projectile

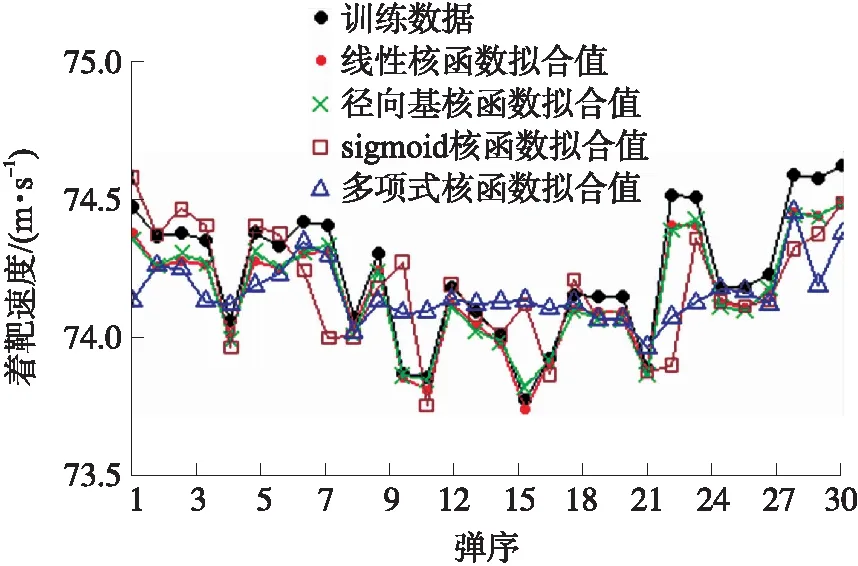
图7 数据信息训练的支持向量回归机不同核函数拟合曲线Fig.7 Fitting curves of different kernel functions of support vector regression machine trained by data information

将测试数据代入到所建模型,即可计算出了数据信息预测出的第31～38发着靶速度,结果如表4所示。计算得到支持向量回归机预测值与实测值的平均相对误差为0.171%,说明数字挖掘的方法挖掘出了更多有用信息,但是预测精度依然不高。

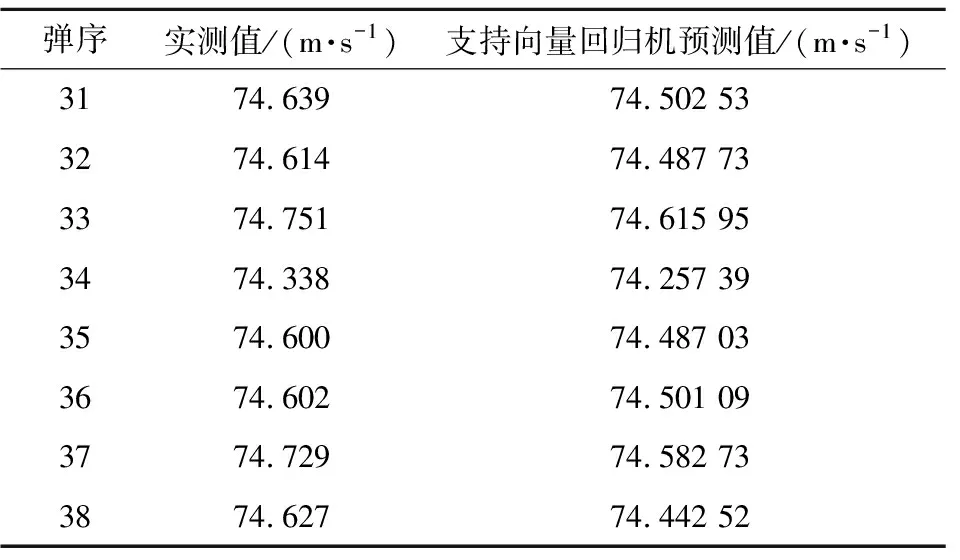
表4 基于数字挖掘的着靶速度预测对比Table 4 Comparison of predicted impact velocity based on data information with measured value

3.3 GM(1,1)模型预测精度分析

可以看出GM(1,1)模型拟合值充分涵盖了训练数据的线性特征。基于GM(1,1)模型的预测着靶速度如表5所示,预测值与实测值的平均相对误差为0.424%。

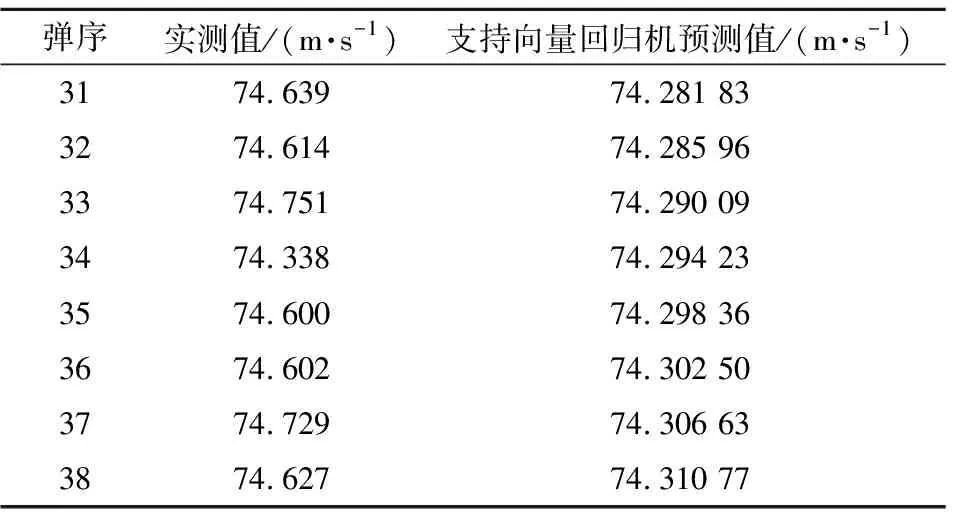
表5 GM(1,1)模型预测值对比Table 5 Comparion of predicted impact velocity based on GM(1,1)model with measured value

3.4 遗传算法优化LSSVM预测精度分析

利用图像信息和数字信息建立的支持向量回归机充分挖掘出了着靶速度中的非线性特征;GM(1,1)模型挖掘出了着靶速度中的线性特征。为了提升预测精度,充分发挥所有模型的预测优势,选择把图像信息支持向量回归机对训练数据的拟合值、数字信息支持向量回归机对训练数据的拟合值、GM(1,1)模型对训练数据的拟合值一同作为特征向量,对应的着靶速度实测值作为目标向量,构建包含非线性特征和线性特征的组合样本数据,然后利用组合样本数据建立遗传算法优化LSSVM模型。模型建立过程中,选择把遗传算法优化LSSVM中的sigma和gama两个参数的寻优范围设置为0～1 000,种群规模设为400,迭代次数设为50,基因突变概率设为0.01,最后搜寻出的最优参数分别为sigma=20.392 85,gama=999.632 50,利用这两个最优参数建立LSSVM模型。再把图像信息支持向量回归机、数字信息支持向量回归机、GM(1,1)模型等预测出的第31～38发着靶速度作为特征向量代入到建立好的遗传算法优化LSSVM模型中,对第31～38发着靶速度进行预测。经过建模预测,第31～38发着靶速度实测值与所有模型预测值如表6所示,关系曲线如图9所示。

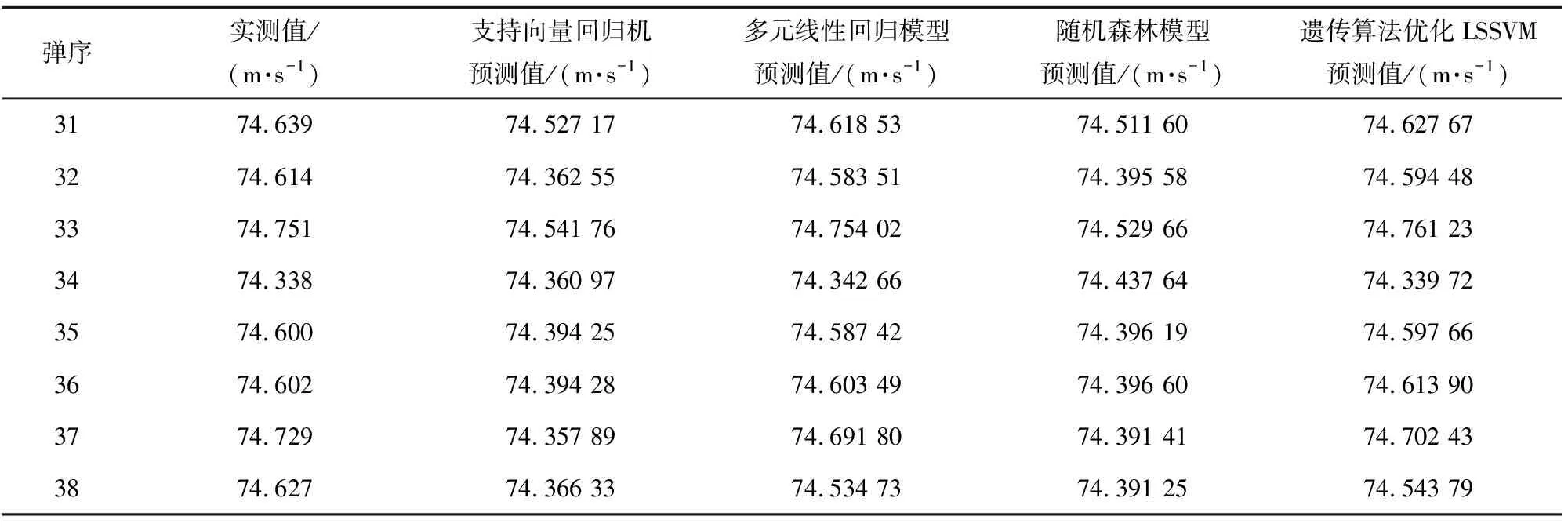
表6 着靶速度实测值与所有模型预测值对比Table 6 Comparision of measured value of impact velocity and predicted values of all models

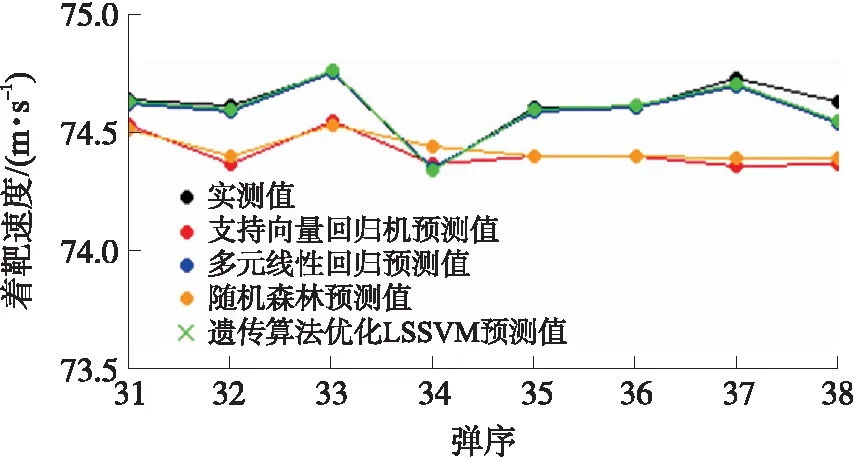
图9 各模型预测值对比Fig.9 Comparison of predicted target velocity of all models

从图9可以看出遗传算法优化LSSVM预测值与实测值最为吻合,计算得到支持向量回归机、多元线性回归模型、随机森林和遗传算法优化LSSVM的预测值与实测值的平均相对误差分别为0.275%、0.034%、0.0276%和0.028%,所以遗传算法优化LSSVM预测精度最高。遗传算法优化LSSVM预测值与实测值的绝对误差如图10所示。可以看出,遗传算法优化LSSVM单项预测误差基本小于1‰的误差标准,预测出的数据可以作为缺失着靶速度的补充数据。

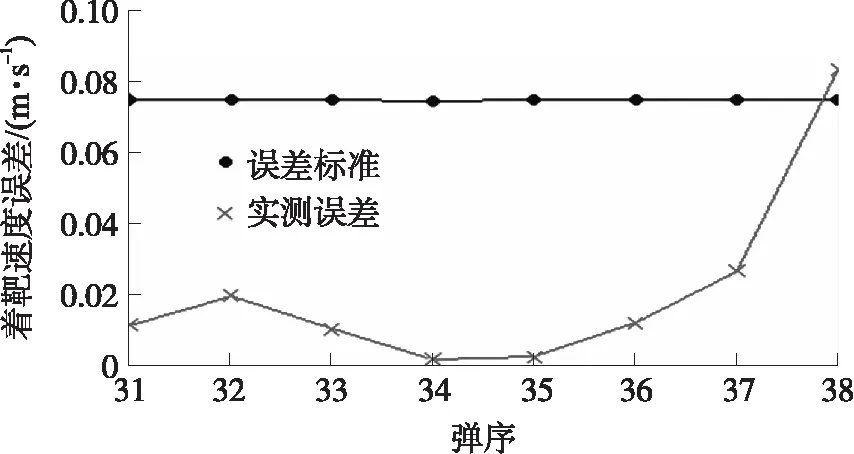
图10 遗传算法优化LSSVM预测值与实测值绝对误差和误差标准关系曲线Fig.10 Genetic algorithm optimizes the relationship curve of absolute error and error standard between predicted value and measured value of LSSVM

4 结论

把弹丸着靶时刻的图像信息和数字信息进行组合,同时把支持向量机、GM(1,1)模型和遗传算法优化LSSVM模型进行融合,组合样本包含非线性成分和线性成分,多模型融合挖掘出了线性特征和非线性特征。研究结果表明:

①遗传算法优化LSSVM预测精度更高,整体预测精度和单项预测精度均达到了标准精度要求,表明所采用的方法可以作为着靶速度预测模型。

②实际上,由于数据量较少,无法训练出稳定的神经网络模型,较为适合建立支持向量机模型,下一步的研究重点是当数据量较大时,如何训练出稳定可靠的神经网络进行建模预测,同时对比支持向量机,检验两个模型预测精度的高低。