基于重新参数化的Bézier曲面求交算法

庞乾一,王振飞,陈小雕

(杭州电子科技大学计算机学院,浙江 杭州 310018)

0 引 言

参数曲面求交是计算机辅助几何设计中基本且重要的问题,也是布尔运算的基础。Bézier曲面和NURBS曲面作为最常用的参数曲面,其求交运算广泛应用于计算机动画[1]、曲面裁剪[2]、数控加工[3]、制造仿真[4]、地质建模[5]等领域。常用的Bézier参数曲面求交方法包括代数法[4]、网格离散法[6]、迭代法[7]、跟踪法[8]等。代数法将2个参数曲面相交问题转化为非线性方程组的求解问题,仅在计算低阶曲面相交时有效,虽然可以通过函数合成[9]获得相交线的精确表示,但其阶数过高,无法在实际中使用。网格离散法将曲面离散为由三角平面片组成的网格,将参数曲面相交问题转化为三角形面片之间的求交运算,通用性强,但曲面的划分需要足够细密,计算耗时明显增加。迭代法根据初始交点在2个曲面上的投影点,通过四参数迭代法求解下一交点,不能单独使用迭代法,且要求交点初值尽可能准确,否则迭代不收敛,无法得到满足精度要求的交点。跟踪法从提前求出的初始交点出发,根据交线的几何特性,按照一定的步长迭代计算后继交点,将这些离散点按顺序连接并再次用B样条拟合。跟踪法存在漏交问题,在法向共线点处的跟踪方向产生的交点不连续,且收敛速度慢,不稳定。文献[10]采用基于交线微分形式的跟踪公式计算后继交点,解决了法向共线点处交点间断不连续的问题,但是,若精度要求很高,则需要很小的跟踪步长,导致跟踪步数和耗时均显著增加。上述曲面求交方法在求得一系列交点之后,需要再次用B样条插值才能表示出交线,且求得的近似曲面交线不能严格落在任何一个曲面上。为此,本文提出一种基于重新参数化的Bézier曲面求交算法,把曲面控制网格的交线近似为曲面的交线,并将其映射到参数域进行拟合,在计算交点个数较少的同时得到较高的逼近精度,且求解出的交线严格落在指定的一个曲面上。

1 算法原理

1.1 曲面控制网格的求交

曲面控制网格求交的基本思想是先将2个曲面都升阶10次从而加密曲面的控制网格,再将控制网格转化为三角网格,每个三角形对应空间中的1个平面,将曲面对求交转化为三角面片对求交。

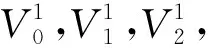
首先,判断三角形T1与三角形T2所在平面是否相交。平面F2的计算公式如下:

X·N2+d2=0

(1)

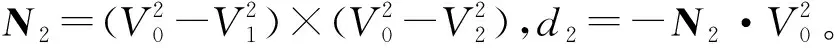
将三角形T1的3个顶点分别代入式(1),得到各顶点到平面F2的距离为:

(2)

然后,根据三角形的3条边与对方三角形的交点求得三角形对的交线段,将所有相交三角形对的交线段依次相连,得到控制网格的交线。

1.2 参数域上的交线拟合

张量积形式的Bézier曲面定义为:

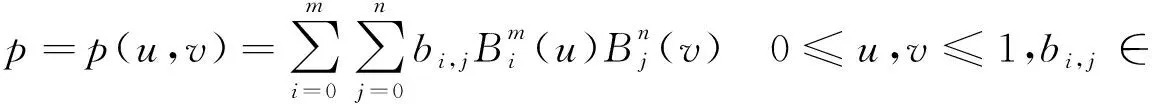
(3)

首先,采用1.1节中求交方法求得交点的重心坐标,将交点直接映射到2个曲面各自的参数域,得到参数域中的交点坐标,并将这些交点按顺序连接,得到控制网格交线映射到参数域中的折线段。由于交点在两曲面的控制网格重心坐标并不相同,所以映射到两曲面各自参数域中的折线段也不相同。

然后,用分段2次均匀B样条分别拟合2个曲面参数域中的折线段。B样条的节点矢量采用均匀节点,即

(4)

式中,r为B样条的拟合次数,k为节点矢量的个数,q为B样条控制顶点的个数。

将2个曲面参数域交线按照u向或者v向分为2段,对这2段都使用6个控制点的2次B样条曲线进行拟合,得到2个曲面各自参数域中拟合后对应的多段B样条曲线。

1.3 重新参数化函数的牛顿迭代求精

将2个曲面参数域中的分段2次B样条曲线作为重新参数化函数,分别代入到2个曲面中,得到曲面上的2条曲线。当这2条曲线之间的Hausdorff距离足够小时,可将其中1条曲线当作2个曲面的交线。由此,设置每一段的牛顿迭代目标函数为:

(5)

从1.2节曲线的分段参数区间内映射到参数域的交点值中均匀取样4个点,作为牛顿迭代的初始值。因为给出的初始值已是较为接近的结果,所以点映射到参数域经过不超过10次的迭代即可使得目标函数小于某个阈值,从而可以认为迭代得到的结果就是最终的近似交线。设置最大迭代次数为30次,如果某段拟合结果的Hausdorff距离在达到最大迭代次数时的结果仍然不满足精度要求,就将该段按照u向或者v向二分,然后再分别用2次B样条拟合迭代求解。

2 实例分析

通过2个数值实例来验证本文提出算法的有效性。算法的控制参数如下:牛顿迭代目标函数的精度为10-7,Hausdorff距离阈值设定为10-3,迭代最大次数为30。实验在CPU为Intel(R) Core(TM) i5-6300HQ 2.3 GHz,内存为12 GB的64位win10操作系统的PC上运行。

例12个2×2次Bézier曲面相交,Hausdorff距离阈值为10-3。

运用本文算法得到参数域分段2次B样条拟合曲线,并代入其中1个曲面得到的交线如图1所示。

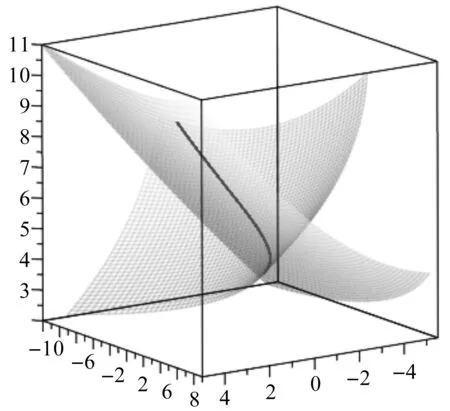
图1 本文算法求得的曲面1和曲面2交线图

曲面1和曲面2的参数域拟合图分别如图2和图3所示。

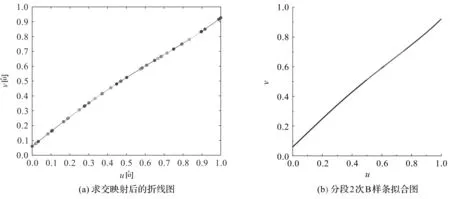
图2 曲面1的参数域拟合图

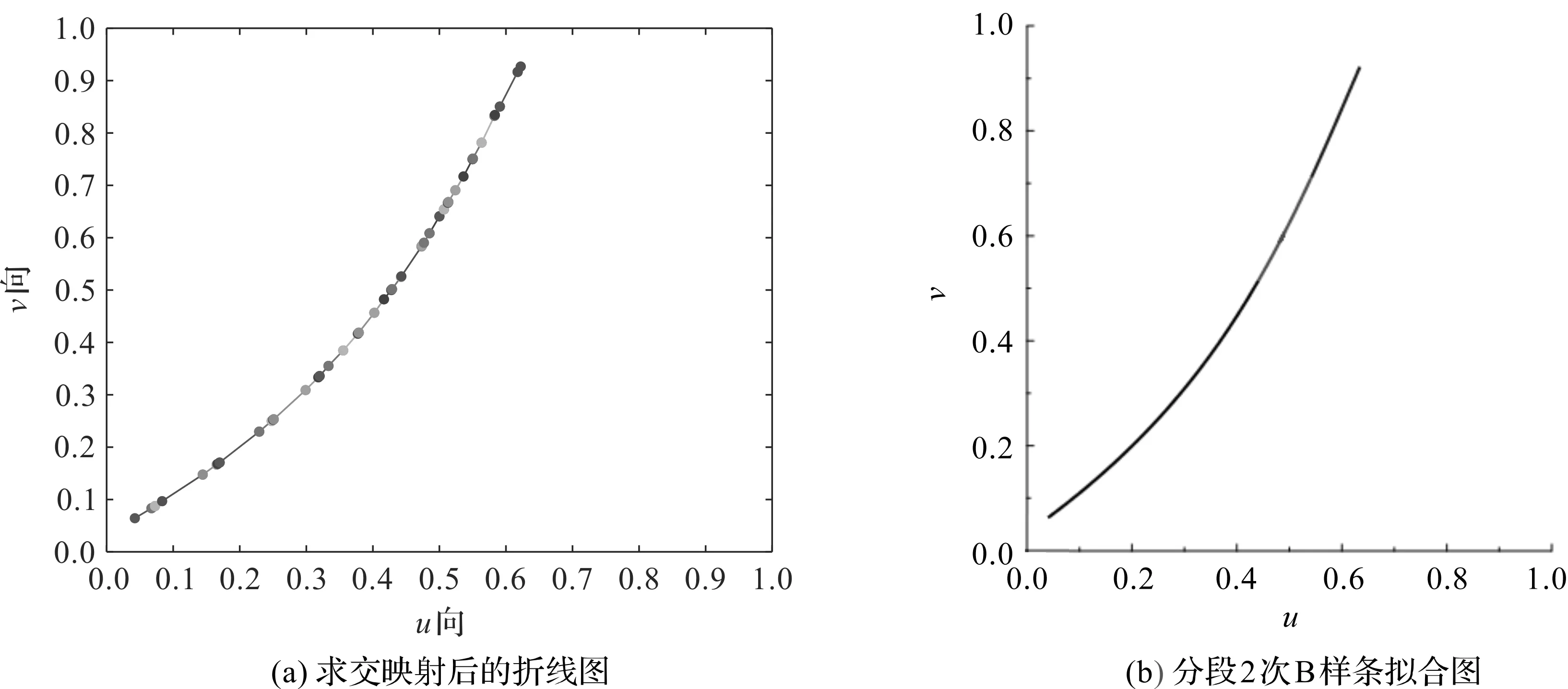
图3 曲面2的参数域拟合图

从图2和图3可以看出,只要经过2次二分即可得到满足Hausdorff距离精度要求的参数域函数。

例22个2×2次Bézier曲面相交,设定Hausdorff距离阈值为10-3。

运用本文算法得到参数域分段2次B样条拟合曲线,并代入其中1个曲面得到的交线如图4所示。

图4 本文算法求得的曲面3和曲面4交线图

曲面3和曲面4的参数域拟合图分别如图5和图6所示。

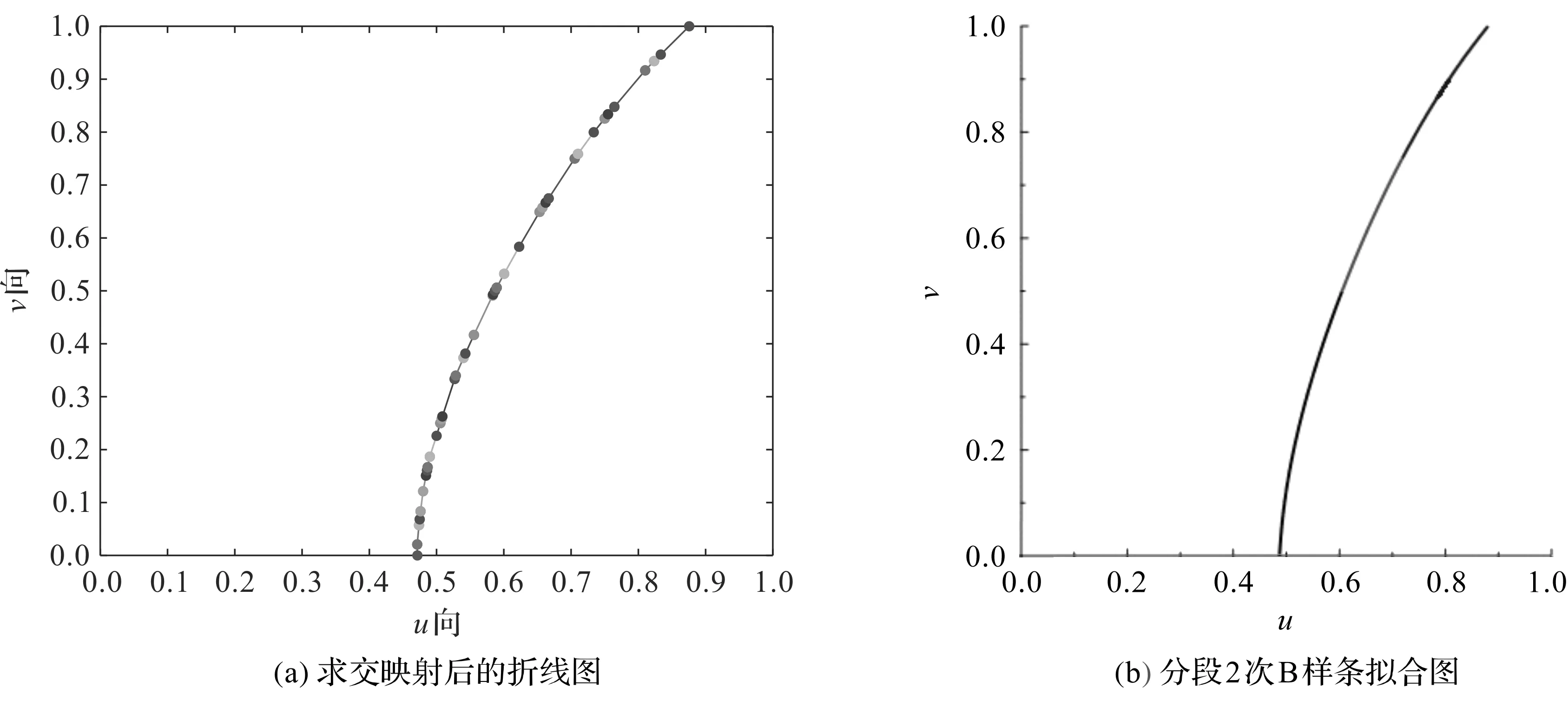
图5 曲面3的参数域拟合图

图6 曲面4的参数域拟合图

分别采用本文算法和传统跟踪法进行求交结果精度的比较。传统跟踪法在给出初始点之后,以不同的步长进行跟踪,再将求得的交点用3次B样条插值,得到最终的近似交线,此交线与精确交线的Hausdorff距离值如表1所示,本文算法求得的交线与精确交线的Hausdorff距离如表2所示。

表1 传统跟踪法的求交结果与精确交线的Hausdorff距离

表2 本文算法的求交结果与精确交线的Hausdorff距离

从表1和表2可知,与传统的跟踪算法比较,本文算法在二分2次时精度值即可达到10-3。因为本文算法先对曲面进行有限次升阶,再求控制网格交线从而得到初始值,该初始值已较为接近结果,所以,2个实例中,经过2～3次的区间二分,每段交线的迭代次数不超过10次即可得到满足精度要求的交线。同时,本文算法中,每段交线在参数域上都是用6个控制点,2次B样条拟合,每段端点处有重叠,所以二分3次的总控制顶点数只有21个,顶点数明显少于传统跟踪法。

3 结束语

本文提出一种基于重新参数化的Bézier曲面求交算法,在计算交点个数更少的同时,获得更高的逼近精度,且交线严格落在其中一个指定的曲面上。算法仍然有较大的改进空间,拟合交点的选取及优化可进一步提升逼近精度。此外,若参数域内对应的曲线形状较为复杂,则需将参数域的交线分为较多段拟合才能得到较为精确的结果,数值计算的耗时和计算稳定性将面临更大的挑战。