一种基于串行消除列表的多比特翻转译码算法

张 旭,刘顺兰,李正杰

(杭州电子科技大学电子信息学院,浙江 杭州 310018)

0 引 言

极化码[1]是首个被证明可以达到信道容量的纠错码,具有较低的编译码复杂度,被第三代合作伙伴计划(3rd Generation Partnership Project,3GPP)确定为5G eMBB场景下控制信道编码方案,成功入选5G标准。极化码的码长越趋近于无穷,其极化效果越好。但是,在中短码长情况下,极化效果较差。为了提高极化码的纠错效果,Ariken[1]提出一种串行抵消译码(Successive Cancellation,SC)算法,但在有限码长情况下,性能并不理想;于是,Tal等[2]提出一种串行抵消列表译码(Successive Cancellation List Decoding,SCL)算法,通过增加列表数量来扩大译码的路径,提升了译码性能。SCL译码算法是目前最常用的译码方法。为了进一步降低极化码的误码率,提高极化码的译码性能,Niu等[3]提出一种循环冗余校验(Cyclic Redundancy Check,CRC)级联Polar的SCL译码(CRC Aided SCL,CA-SCL)算法,在SCL的译码列表中挑选出正确的译码结果,保证译码的准确性;Elkelesh等[4]设计了一种置信传播列表译码器,其译码性能与常用的SCL译码器相似。文献[5]将比特翻转原理应用到极化码的SC译码算法中,提出一种串行抵消翻转(Successive Cancellation Filp,SCF)译码算法,在SC译码错误时,通过比特翻转进行矫正,但只能纠正1位错误。于是,动态SCF算法[6]、分段SCF算法[7-8]被相继提出。同样,SCL算法也可应用比特翻转,文献[9]提出一种串行抵消列表比特翻转(Successive Cancellation List bit-Flip,SCLF)译码算法,性能得到较大提升,但也只能纠正1位错误。为了更好地提升误块率性能,崔建明等[10]结合比特翻转与分段原理,提出一种分段CRC辅助极化码SCL比特翻转译码算法;袁建国等[11]为了兼顾译码算法的性能与复杂度,提出一种快速串行抵消列表翻转(Fast Successive Cancellation List Flip,FSCLF)译码算法,通过引入信息比特结点和单奇偶校验(Single-Parity-Check,SPC)结点来降低译码复杂度,提高了译码性能。受SCF译码算法的启发,本文结合SCF译码与SCL译码,提出一种基于串行消除列表的多比特翻转译码算法。

1 极化码原理

1.1 极化码

极化码是一种运用信道极化理论的信道编码方式,与其他信道编码技术最大的不同在于极化码可以进行信道极化,并利用信道极化产生的极化现象进行信息传输。当极化码的码长不断增大并趋于无穷时,其各个子信道逐渐呈现两极分化现象,一部分信道容量趋近于1,另一部分趋近于0。在传输信息时,可以选择可靠度较高即信道容量趋近于1的信道进行信息传输,剩下的信道作为冻结位。极化码可表示为(N,K,A,uAc),N表示极化码的码长,K表示信息位的长度,A表示信息位比特的集合,其补集Ac表示固定子信道的索引集合,其上标c为补集符号,uAc表示冻结比特序列[12],根据极化码的编码原理,编码后的码字为:

(1)

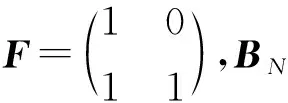
(2)

式中,GN(A)为由A中元素对应的行构成的GN的子矩阵,GN(Ac)为由Ac中元素对应的行构成的GN的子矩阵,⊕表示模2加。

1.2 SC和SCL译码

(3)

再根据LLR值对信息位进行硬判决,得到:

(4)

式(3)可表示为:

(5)

(6)

备忘录为双方建立了一个合作框架，未来双方将在该框架下研究利用各自的独特能力、专门知识和客户关系开展一系列商业合作的可行性。

(7)

(8)

式中,us∈{0,1}。SC算法根据式(7)和式(8)计算得到每个节点的LLR后,再根据式(4)对每个信息比特进行判决,得到译码结果。但是,这种方法是串行译码,容易出现错误传播。

在SC算法基础上,SCL译码算法同时保留L条SC译码路径,进行并行译码,每条路径都是根据路径度量(Path Metric, PM)[13]筛选得到的,其表达式为:

(9)

1.3 SCF译码

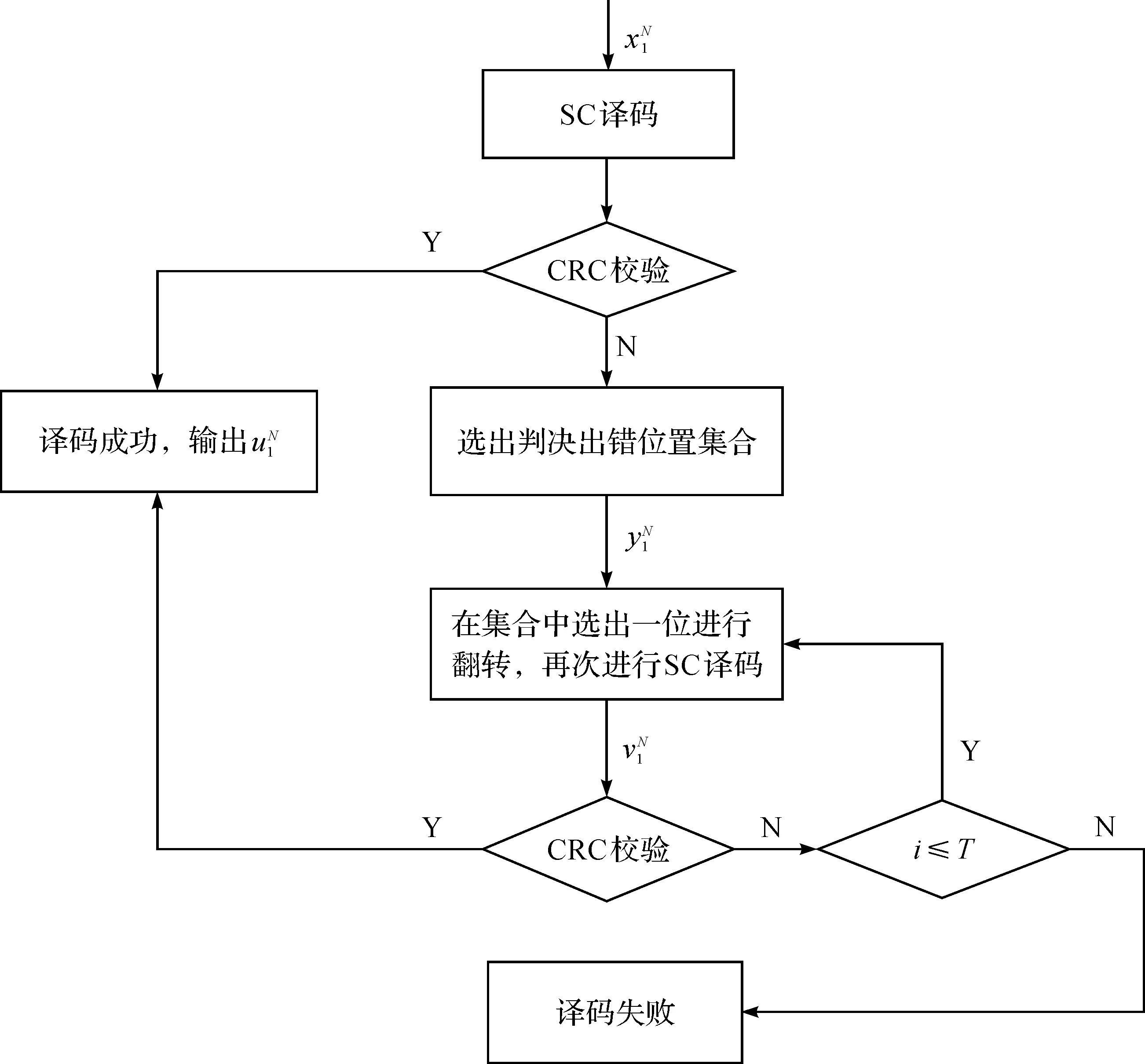
图1 SCF译码算法流程图

2 基于串行消除列表的多比特翻转译码算法

虽然SCF译码算法的性能优于SC译码算法,但每次只能对其中1位不可靠信息位进行翻转,不能进行多位翻转,译码性能提升有限。所以,在SCF译码算法的基础上,本文提出一种基于串行消除列表的多比特翻转译码算法,在编码时,将极化码作为内码进行编码,CRC码作为外码进行校验,极化码编码采用高斯构造方法。本文算法的译码流程如图2所示。

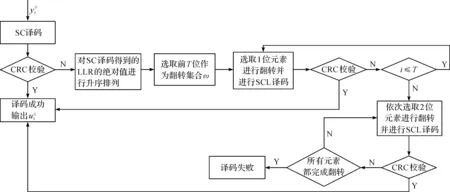
图2 基于多比特翻转的串行消除列表译码算法流程

(3)对每个码字的V值进行升序排列,并取前T个最小V值所对应的信息位索引作为翻转集合,其中T表示选取翻转集合元素的个数,ω={ω1,ω2,…,ωT}表示翻转集合,ωi表示翻转集合中第i位元素。

(4)对所有信息位进行SCL译码,并判断L条译码路径中是否有路径通过CRC校验,如果有则结束译码,否则选取翻转集合中下一位元素,重新进行SCL译码,直到有路径通过校验;如果T次尝试均不成功,则执行下一步。

(5)从ω={ω1,ω2,…,ωT}中依次选取V值较小的2位进行翻转,再进行SCL译码,译码结果若未通过CRC校验,则重新选取翻转位进行SCL译码。若通过校验,则输出译码结果。当所有尝试均未通过CRC校验,则译码失败。

3 仿真实验与分析

在MATLAB平台上,加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下,采用BPSK调制方式进行仿真实验。极化码的码率为0.5,蒙特卡罗仿真次数为10 000次。

码长N为512,SCL的列表宽度L为4,选取不同翻转集合个数T,采用本文提出的基于串行消除列表的多比特翻转译码算法进行仿真,得到误块率(Block Error Rate,BLER)如图3所示。

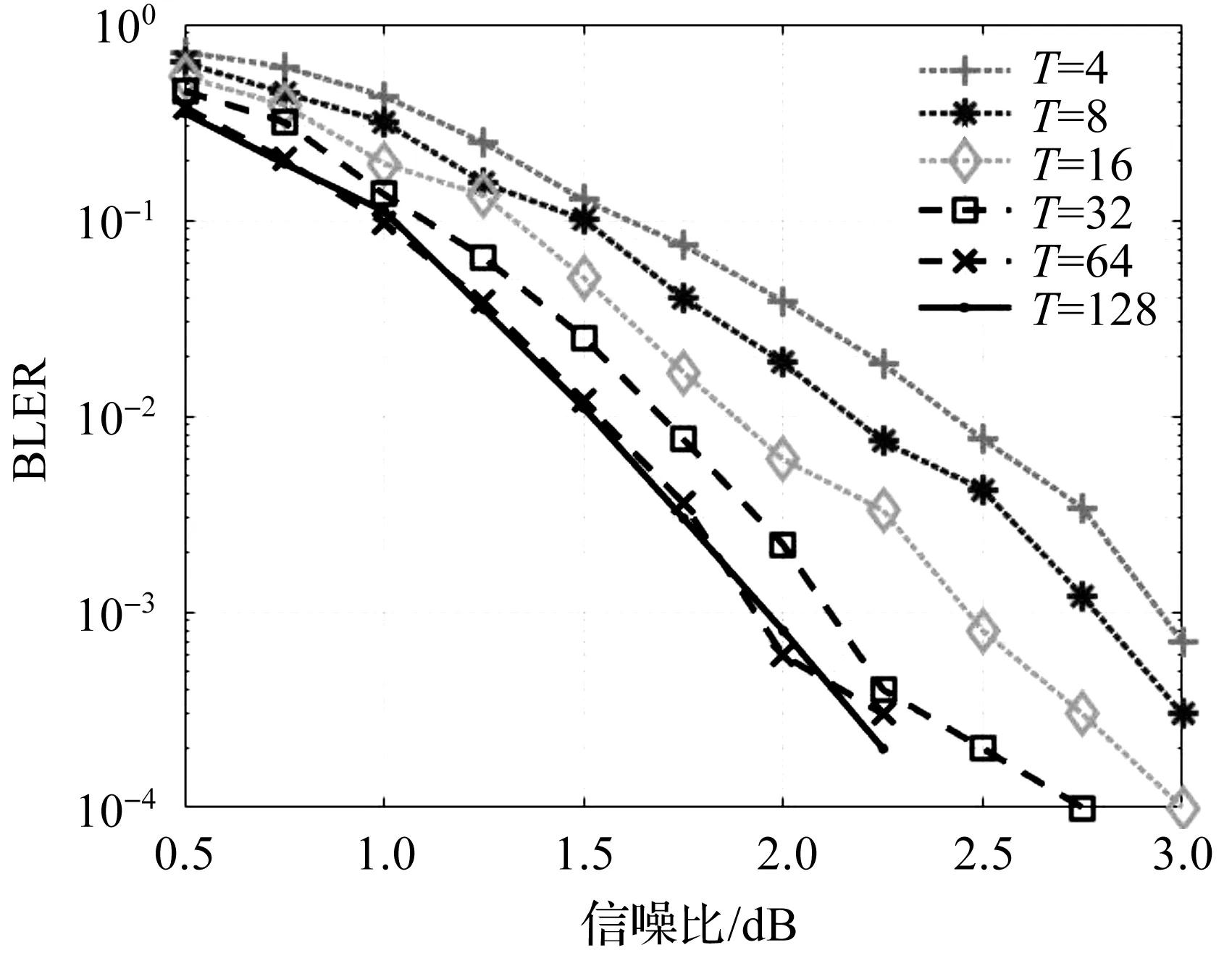
图3 不同T值下,本文算法的误块率

从图3可以看出,在相同信噪比情况下,T值越大,误块率越小。当T为码长512的1/8,即T=64时,误块率的提升几乎达到极限,说明T对译码性能的提升有一定的影响。

码长N为512,码率为0.5,T为64,选取不同列表宽度L,采用本文算法进行仿真,得到误块率如图4所示。

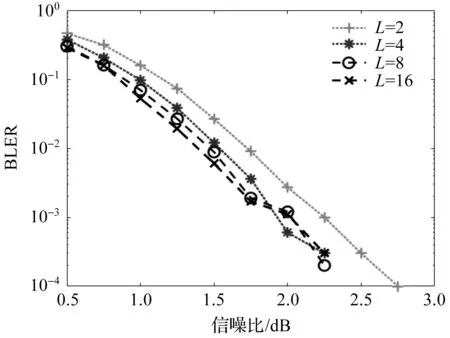
图4 不同L值下,本文算法的误块率

从图4可以看出,随着L的增大,误块率随之变小。

列表宽度L为4,翻转集合元素的个数T为8,选取不同码长N,采用本文算法进行仿真,得到误块率如图5所示。

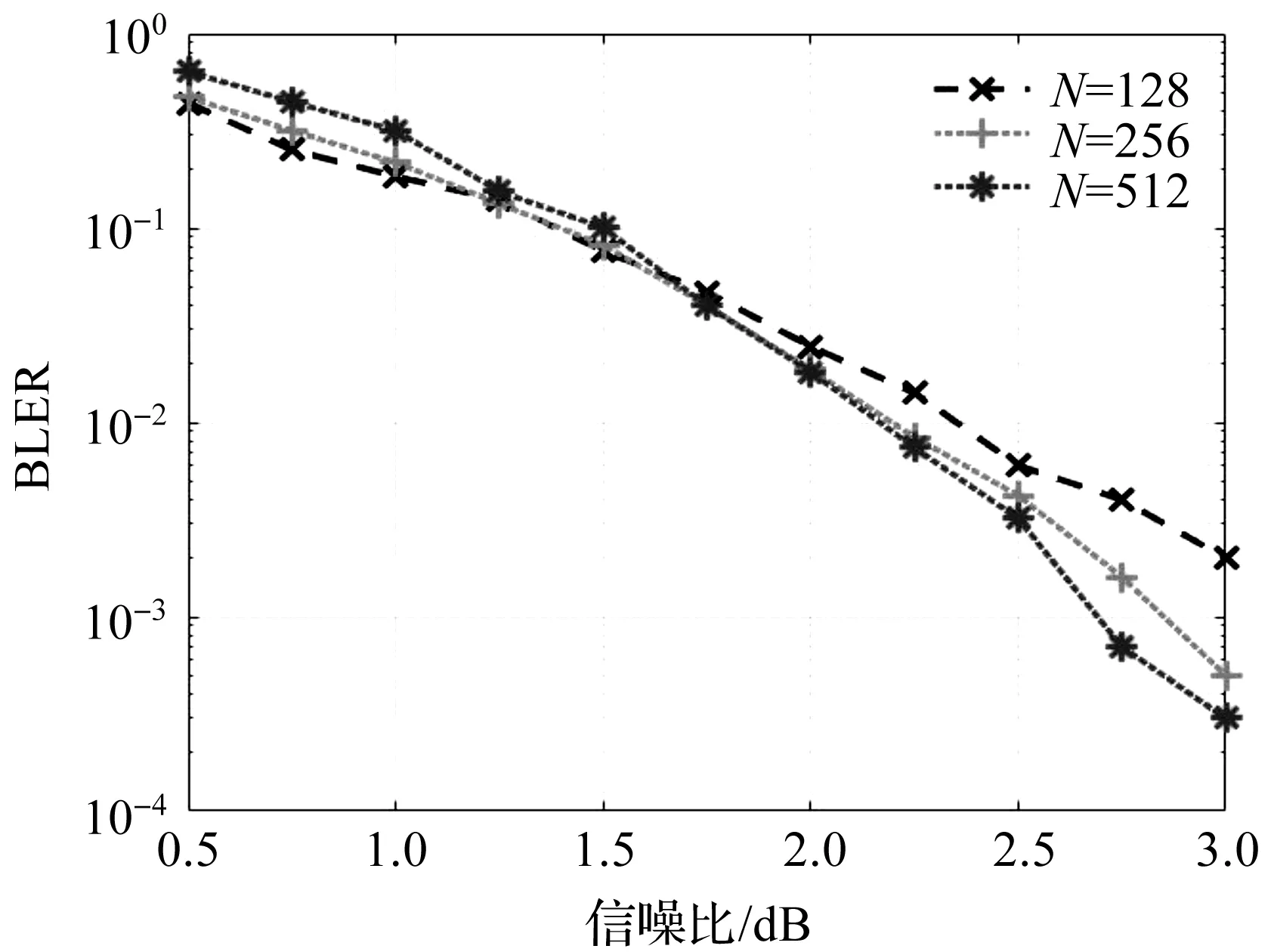
图5 不同N值下,本文算法的误块率

从图5可以看出,随着码长N的增大,误块率随之变小,性能越来越优,当误块率为10-3时,相比于码长为256,本文算法在码长为512时获得了大约0.1 dB的增益。

列表宽度L为4,翻转集合元素的个数T为码长的1/8,选取不同码长N,采用本文算法进行仿真,得到误块率如图6所示。

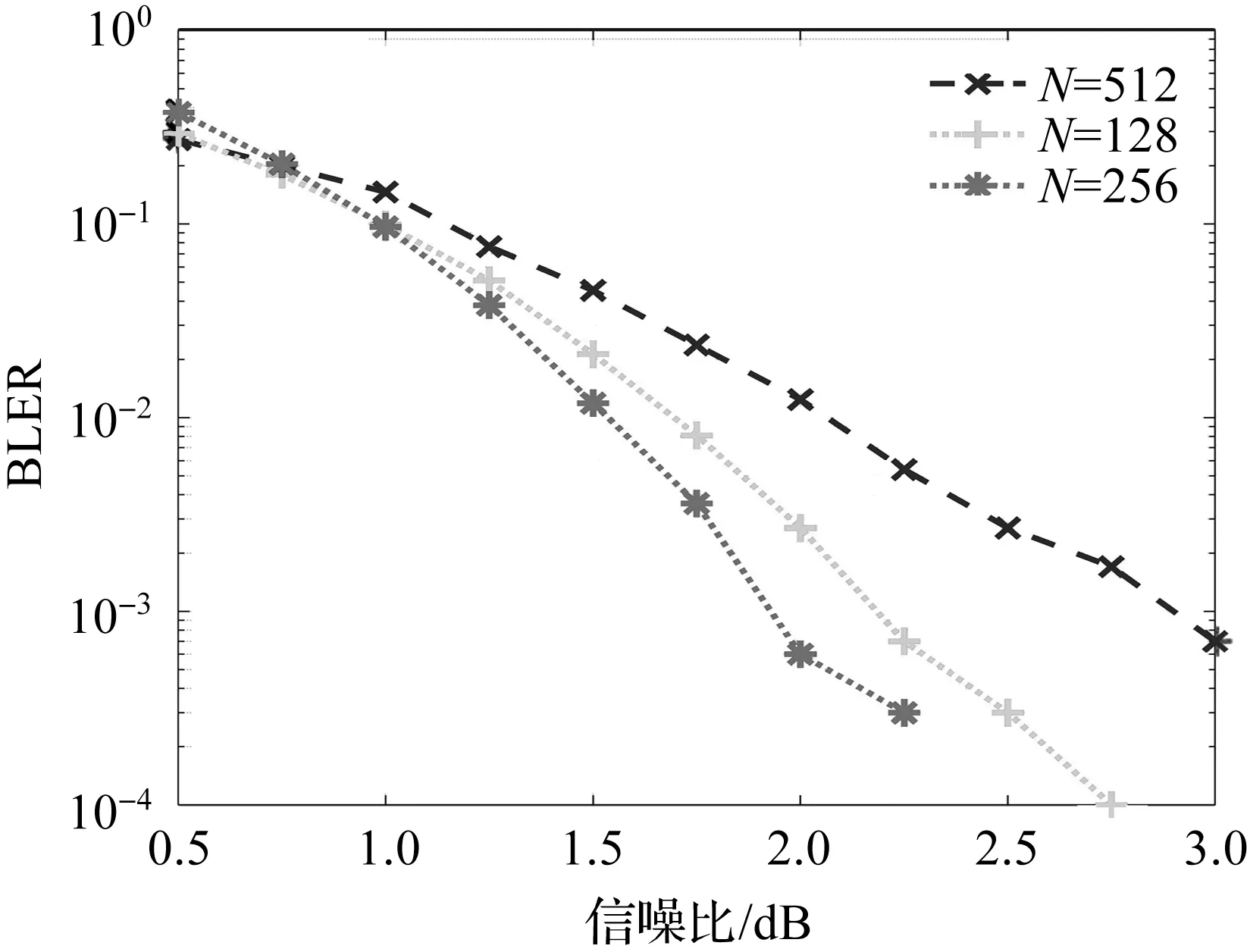
图6 不同N值且T为码长的1/8下,本文算法的误块率

从图6可以看出,随着N的增加,误块率随之变小,当误块率为10-3时,相比于码长为256,码长为512时获得了大约0.2 dB的增益。

码长N为512,列表宽度L为4,翻转集合元素的个数T为64时,分别采用本文算法、SC译码算法、SCL译码算法、文献[5]中SCF译码算法、文献[9]中SCLF译码算法、文献[3]中CA-SCL译码算法进行仿真,得到6种算法的误块率如图7所示。

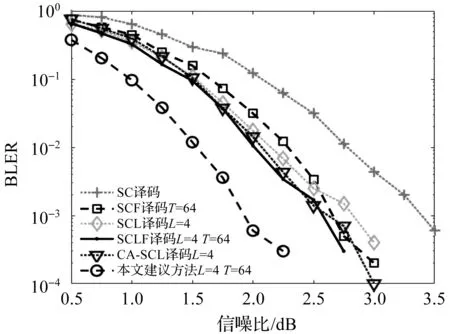
图7 不同算法的误块率对比

从图7可以看出,当误块率为10-3时,本文算法的误块率最小,相较于SCF译码算法、SCL译码算法、CA-SCL译码算法、SCLF译码算法、SC译码算法分别获得了0.70 dB,0.90 dB,0.65 dB,0.60 dB,1.50 dB的增益。

4 结束语

为了进一步提高极化码在中短码长下的译码性能,本文在SCF译码算法的基础上,提出一种基于串行消除列表的多比特翻转译码算法。当SC译码发生错误时,根据SC译码得到的对数似然比绝对值选出翻转集合,并对其进行多比特翻转。但是,本文只是在AWGN信道下进行了仿真实验,后续将在其他通信环境下展开进一步研究。