基于前馈型神经网络解变系数分数阶积分微分方程

杨刘盼,郭安祺,邵新平

(杭州电子科技大学理学院,浙江 杭州 310018)

0 引 言

分数阶积分微分方程是众多物理现象的建模工具。但是,大多数情况下,求分数阶积分微分方程解析解非常困难。现阶段,对分数阶Volterra-Fredholm积分微分方程和分数阶Fredholm积分微分方程的数值解法主要有同伦分析法[1]、改进的Laplace分解法[2]、Adomian分解法[3]、Legendre多项式近似法[4]等,这些方法的主要特点是将求解分数阶Volterra-Fredholm积分微分方程和分数阶Fredholm积分微分方程归结为求解一个代数方程,大大降低了求解难度。此外,Bernstein多项式在数学的各个领域扮演着重要角色,在微积分方程和近似解中都会使用Bernstein多项式[5-7]。相较于Legendre多项式、Chebyshev多项式和Laguerre多项式等,Bernstein多项式构造简单,且拥有成熟的逼近估计阶理论[8]。随着神经网络研究的不断发展,计算技术的不断提高,基函数神经网络的逼近功能成为求解微积分方程数值解的热门算法之一。Jafarian等[9]提出一种基于神经网络和幂级数相结合的方法用于求解分数阶Fredholm积分微分方程,具有较高的计算精度;李娜等[10]提出一种基于函数逼近的Chebyshev神经网络求解非线性Fredholm积分方程的方法,与现有算法比较,Chebyshev神经网络误差稳定,更有效地逼近精确解。与数值求解方法相比,神经网络具有良好的泛化能力和较高的计算精度。本文提出一种基于Bernstein多项式的前馈型神经网络求解变系数分数Fredholm积分微分方程的新方法,将Bernstein多项式的系数作为权重,构造前馈型神经网络,采用梯度下降法学习权重,得到近似解。

1 预备知识

本文求解的变系数分数阶Fredholm积分微分方程如下:

(1)

式中,初值条件uj(0)=bj,j=0,1,2,…,r-1,r-10,k(x,t)为区域0≤x,t≤1已知的核函数,g(x)和ai(x)为x∈[0,1]上的已知函数,u(x)为未知函数,Dαi为Caputo分数阶微分算子[4]。

建立客史档案，把握顾客需求。市场营销理论告诉我们，只有真正把握顾客的需求，才能提供令宾客满意的服务，才能提高酒店的竞争力。因此，酒店必须要建立起独一无二的客史档案。那么酒店该从哪些方面建立客史档案呢？首先，酒店要从收集顾客资料着手，全程跟踪，完整准确的建立常客档案；其次，要应用计算机进行数据技术开发，建立详尽而细微的顾客需求档案，最终建立顾客信息库。

1.1 Bernstein多项式

设函数f∶[0,1]→R,对于n∈N+,定义f的n阶Bernstein多项式[11]:

(2)

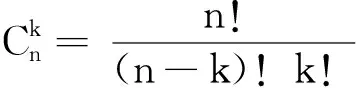
2.2.5 3组小鼠最大呼气中期流速比较 对照组和脂多糖组在6、18、36 h后的最大呼气中期流速比较，差异无统计学意义(P>0.05)。18、36 h后，甲强龙组最大呼气中期流速较脂多糖组升高，差异有统计学意义(P<0.05)；6 h后，两组最大呼气中期流速比较，差异无统计学意义(P>0.05)。见图2e。

1.2 Caputo分数阶导数

定义Caputo分数阶导数

(3)

特别地,对于幂函数xβ,β>0,有

(4)

2 分数阶微积分的Bernstein多项式矩阵运算

对于变系数的分数阶Fredholm积分微分方程

根据病虫害生长所需的温度、湿度条件，可以通过调节温度、湿度、光照等条件创造不利于病虫害发生的环境。以黄瓜霜霉病防治为例，若发病较重，可以进行高温闷棚，维持棚内温度45℃，持续2 h后再放风，连续两三次即可有效控制病害［5］。

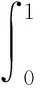
(5)

任意函数u(x)∈C[0,1],都可用Bernstein多项式近似为:

世界欠了中国人一个诺贝尔奖！世界更欠了赵忠尧一个诺贝尔奖！可赵忠尧却对此毫不在意，因为他远渡重洋不是为了学位，更不是为了拿诺奖，而是为自己的国家和民族学到最前沿的科学和技术！

经皮尔逊相关系数分析，喉源性咳嗽的局部病理改变与其中医辨证分型有关，呈高度正相关，r=0.819，P＜0.05。

(6)

则式(5)表示为:

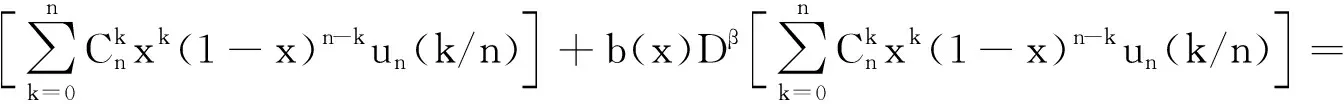
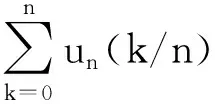
(7)

可得:

(8)

(9)

(10)

其中γ=α,β,k=0,1,2,…,n。由Caputo分数阶导数的定义,式(10)可转化为如下矩阵形式:

(11)

(12)

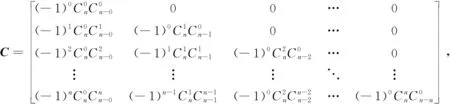
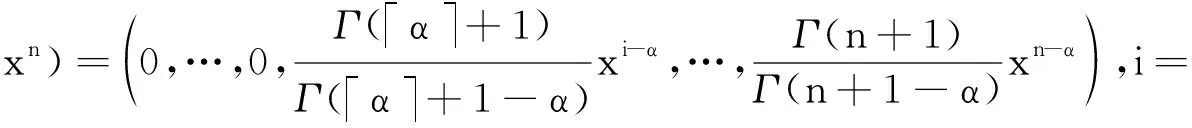
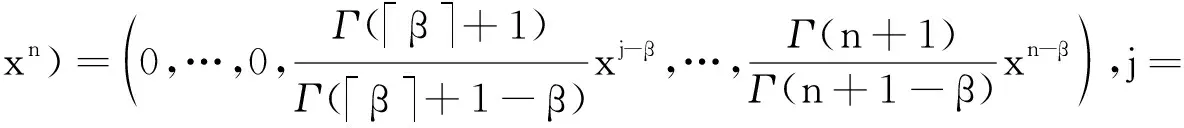
运用Bernstein配点法将式(7)转化为矩阵形式。取m+1个配置点,

1.1.2 仪器。U3000高效液相色谱仪(配置DAD检测器，美国戴安公司)；MS205DU电子分析天平(瑞士METTLERROLEDD公司)；EXceed-AC-24超纯水机(成都康宁实验专用纯水设备)；GT SONIC-P3超声波清洗仪(固特超声股份有限公司)。

(13)

将式(11)、式(12)和式(13)代入式(7),得到:

GW=H

(14)

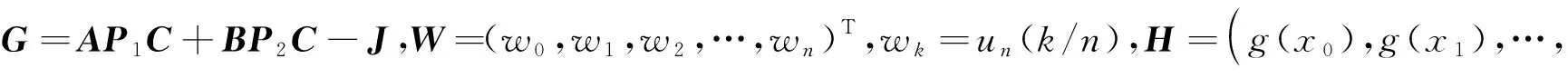
3 基于Bernstein多项式的前馈型神经网络

本文采用Bernstein函数扩展块作为神经网络的隐含层,wk=un(k/n)作为Bernstein函数扩展块到输出层的权重,输入向量x=(x0,x1,…,xm)进入输入层后,通过Bernstein函数扩展块到输出层,进行Bernstein多项式的展开,构造了基于Bernstein多项式的前馈型神经网络,其网络拓扑结构如图1所示。

将损失函数转化为矩阵形式,

罗瑞显然有点着急了，结结巴巴地解释：“我也没想到她会那么激动，我不是故意的。哎，警官大人，你不会怀疑我吧？！我可没杀她！”

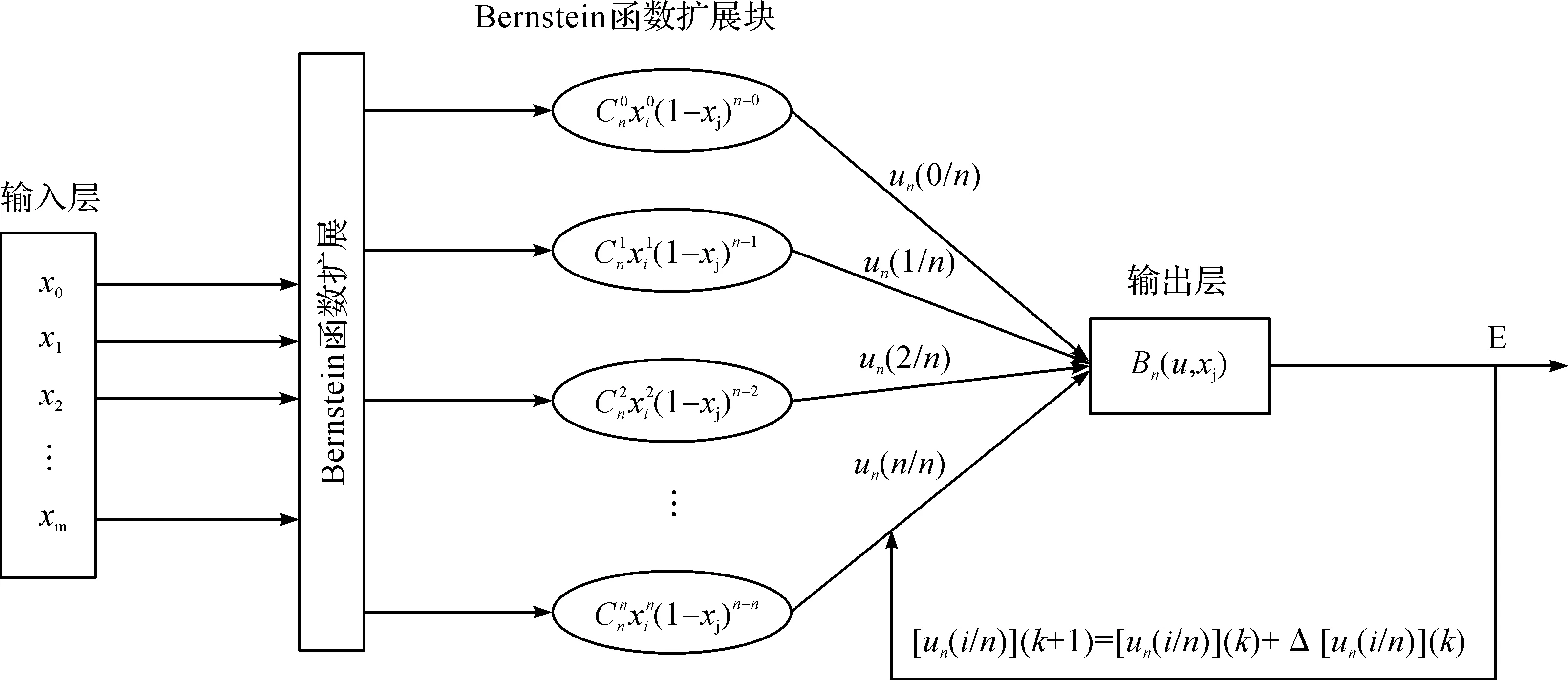
图1 基于Bernstein多项式的前馈型神经网络拓扑结构

证明动量项可以在维持算法稳定的前提下加速收敛,不妨取α=0,

在2018年4月的时候，我国落实了有关金融机构管理业务的指导意见的条例，条例中要求商业银行必须有效地提升对资产的管理能力，所以商业银行相关的投资和风险管理能力如果能够在市场中充分体现出来，就能大幅度提高商业银行的综合实力，零售网点的转型的成果也能更加显著。要想做好管理工作，就需要工作人员具有较高的专业技能水平和扎实的知识基础，企业要吸收更多金融市场上的人才，还可以成立专业的工作团队，建设出一支高素养和高职业技能的工作队伍。此外，还可以设立专门的资管公司，可以更好地进行管理，提高管理的效率。

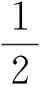
经手术治疗结合护理干预后,26例血管瘤患者的手术成功率达100%,1例出现并发症,得到及时处理,护理满意度达92.3%(24/26)。

(15)

将配置点xj作为神经网络的输入向量,对权重W进行学习,在损失函数最小化的约束下,使得神经网络获得较高的逼近精度。采用梯度下降法对式(14)进行求解,并按以下规则对权重W进行迭代更新,

(b)通过输出向量计算神经网络的当前误差E;

W(i+1)=W(i)+ΔW(i)

(16)

(17)

式中,i为迭代次数,α∈[0,1)为动量项系数,η为神经网络学习率。

综上所述,本文提出的基于Bernstein多项式的前馈型神经网络权重W学习算法流程如下。

(1)令α>0,η>0,设定目标误差Emax>0,随机初始化权重W。

(c)利用损失函数和梯度下降法调整权重W。

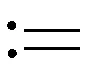
(a)通过输入向量和权重W计算神经网络的当前输出向量;

防错系统的运用在国外发展得很成熟，不同的公司都有适合本公司生产特点的防错控制系统。国外的通用性防错系统价格昂贵，并且对于国内大量的企业都不适用。目前国内制造商在防错系统上处于刚刚起步阶段，没有成熟的防错控制系统[3]。

(4)如果E>Emax,将E设为0,返回步骤3,开始新的训练周期;如果E≤Emax,终止训练。

4 收敛性分析

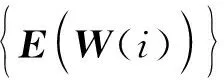
取损失函数为

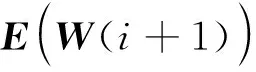
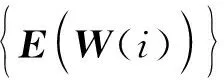
政治类课程的安排，目的是使学生提高政治意识，培养学生参政议政能力，了解和掌握国内外政治经济发展动态，深刻理解中国共产党带领全国人民从站起来、富起来到强起来的伟大历程。调查结果显示，大部分学生认为政治课的学习效果多依赖于教师上课的方法与技巧，希望任课教师在课上能够多讲一些与历史有关，与中共党史有关的伟大事迹，以调动学生课上学习的积极性，激发学生的爱国情怀。

刘丽芳披着睡衣坐在床头，怀抱着一个毛茸茸的靠垫，眼神里写满了无辜与无助。彭伟民昨晚没与她同床，睡在另一个房间，一大清早招呼也没打就离开了家。刘丽芳不敢过问。一场突如其来的遭遇酿就了一个非常时期，非常时期的任何一句话都有可能导致战争。刘丽芳不敢冒这个险。如果昨晚什么事情都没发生，也许这个时候的她正在某家超市里逛着，说不定已经选购好了一大堆生活用品。

5 数值实例

通过求解2个变系数分数阶Fredholm积分微分方程来验证本文提出的基于Bernstein多项式构造的前馈型神经网络求解变系数分数阶积分微分方程的可行性和有效性。

例1变系数分数阶Fredholm积分微分方程如下:

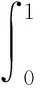
且u(0)=0,u(1)(0)=1,方程的精确解为u(x)=xex。Bernstein多项式阶数n分别为7,8,9,10,11时,采用本文提出的基于Bernstein多项式构造的前馈型神经网络求解方程,得到数值解与精确解的误差如表1所示。

表1 n=7,8,9,10,11时,本文方法求得的数值解与精确解的误差

从表1可以看出,随着Bernstein多项式阶数n的增大,数值解越来越逼近精确解,说明采用本文方法求解变系数分数阶积分微分方程的可行性和有效性。

例2变系数分数阶Fredholm积分微分方程如下:

且u(0)=0,u(1)(0)=0,u(2)(0)=2,方程的精确解为u(x)=x2。当多项式阶数n=7时,分别采用Legendre多项式近似法[6]和本文提出的基于Bernstein多项式构造前馈型神经网络的方法求解方程,得到数值解与精确解的误差如表2所示。

表2 n=7时,不同方法求得的数值解与精确解的误差

从表2可以看出,与Legendre多项式近似法[6]相比,本文提出的基于Bernstein多项式的前馈型神经网络的逼近精度更高。

当Bernstein多项式阶数n=6时,采用本文方法进行求解,得到近似解与精确解、误差函数与迭代次数的关系如图2所示。

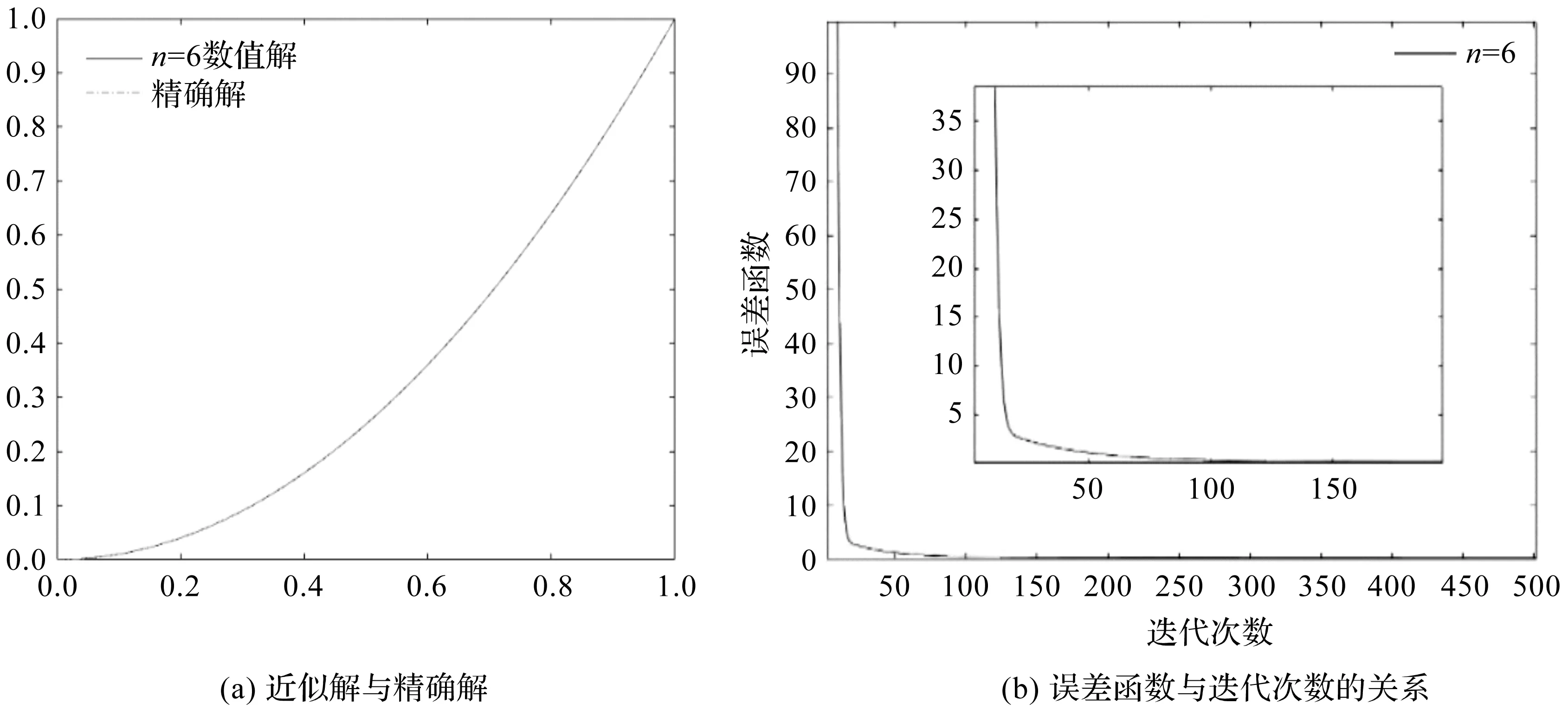
图2 n=6时,本文方法求得的近似解与精确解、误差函数与迭代次数的关系

由图2可以看出,采用本文方法求得的近似解拟合效果很好。同时,当Bernstein多项式阶数n=6,迭代次数在50次内,误差函数迅速下降,最后趋于稳定,进一步验证了本文方法的可行性与有效性。

6 结束语

本文提出一种基于Bernstein多项式的前馈型神经网络解变系数分数阶Fredholm积分微分方程的方法。运用导数阶导数的性质和矩阵运算,将求解方程转化为Bernstein多项式空间上的矩阵形式,并将Bernstein多项式系数作为权重,构造前馈型神经网络,提高了逼近精度。目前,变系数分数阶积分微分方程的相关研究较少,今后将继续深入研究此类问题,得到更有价值的方法用于求解变系数分数阶积分微分方程。