竞合网络下带有事件触发的分布式跟踪研究

李 丽,王 佳,胡鸿翔

(杭州电子科技大学理学院,浙江 杭州 310018)

0 引 言

多智能体系统在电力系统控制、交通控制等领域应用广泛。一致性[1]一直是该领域的研究核心,即通过个体间信息交互使得所有个体状态最终达成共识。在多智能体系统中,个体间频繁的信息交互占用了大量网络资源,甚至导致系统崩溃[2]。事件触发机制通过设计个体间信息交互的事件来减少其交互频次,节约了网络资源[3]。文献[4]比较分析了事件触发采样与传统周期采样,研究发现,事件触发采样可有效降低系统状态更新频率和个体之间的信息通信频次。Hu等[5]研究了二阶多智能体系统的一致性问题,设计的集中式事件触发机制需要每个个体的状态信息。Dimarogonas等[6]从分布式策略出发,针对每个个体,设计了各自的事件触发机制,进而解决了渐近一致性问题。与集中式事件触发机制相比,这类分布式事件触发机制只需要个体的邻居状态信息,更具操作性。进一步地,Fan等[7]在事件触发机制中引入“组合测量”法,不仅有效减少了个体间的交互更新的频率,而且保证了每个个体收敛性能的一致性。文献[8-9]将事件触发机制引入领导者跟随的多智能体系统中,提出一种基于事件触发机制的分布式跟踪方案,成功实现了领导者跟踪一致性。针对二阶个体,Hu等[10]研究了二阶个体系统的领导跟随一致性问题。值得注意的是,在实际网络中,个体间不仅具有合作关系,还有竞争关系,研究合作竞争网络中的群集行为更具现实意义。Hu等[11]在合作竞争网络中研究一致性问题,设计了一种新颖的带有通信时延的事件触发机制。本文探讨合作竞争网络中带有事件触发项的线性系统的分布式两分跟踪问题,设计了一种新型事件触发机制下的分布式协议,实现了多智能体系统的分布式两分跟踪,并排除了Zeno现象。

1 预备知识

1.1 图论知识

针对网络拓扑,本文采用加权图G={V,ε,A}来刻画,其中V={1,…,N}是个体集,ε=V×V是边集,且A=[aij]∈RN×N是图G的权重矩阵,aij≠0⟺{j,i}∈ε。本文中,所研究的图是没有自环的,即aii=0,∀i∈V,同时非零权重可正可负,负权重代表相应个体间为竞争关系。若矩阵是对称的,则网络拓扑是无向的。图中路径指的是从图上一点到另外一点所经过的不会重合的点和边的集合,如果任何2个不同的个体间都有1条路径,则称网络拓扑图G是连通的。个体i的邻居集定义为Ni={j∈V|aij≠0,j≠i}。注意到权重符号有正负,边集ε可分解为ε+与ε-,其中ε+={(j,i)|aij>0},ε-={(j,i)|aij<0}。

定义1对于合作竞争网络图G,如果存在一组个体集的划分{V1,V2}满足V1∪V2=V和V1∩V2=Φ,使得对于任意的i,j∈Vm(m∈{1,2}),aij≥0,并且对于任意的i∈Vm,j∈Vn,m≠n(m,n)∈{1,2},aij<0,则称合作竞争网络图G是结构平衡的。

引理1[12]合作竞争网络图G是结构平衡的当且仅当存在一个规范变换[13]矩阵D=diag{d1,d2,…,dn},其中的元素di∈{1,-1},使得DAD中的元素都非负。其中D对G中节点集提供了一个划分,V1={i|di=1},V2={i|di=-1}。

1.2 符号注解

对于对称矩阵H∈RN×N,λmin(H),λmax(H)分别表示其最小特征值和最大特征值。⊗代表相应矩阵的克罗内克积。1N=[1,…,1]∈RN。

1.3 模型构建

本文主要研究领导跟随者框架下的分布式两分跟踪问题,其中领导者的动力学方程为:

(1)

式中,x0(t)∈Rn表示领导者状态,A∈Rn×n是一个常量矩阵。在研究框架下,共有N个跟随者,其动力学方程为:

(2)

式中,xi(t)∈Rn表示跟随者i的状态,ui(t)∈Rm表示施加在个体i的分布式协议,B∈Rn×m是常量矩阵。

根据系统中个体间的合作竞争关系,本文将分布式控制协议设计为:

(3)

式中,K为分布式增益矩阵。xi(t)-xj(t)代表个体i与其合作邻居间的信息交互,xi(t)+xj(t)代表个体i与其竞争邻居间的信息交互,xi(t)-dix0(t)代表个体i与领导者间的信息交互。显然当ai0=0时,个体i与领导者之间是没有信息交互的。

(4)

式中,H=L+M。为便于理论分析,本文有如下2个假设。

假设1矩阵对(A,B)是可控的。

假设2对于任意一个跟随者i,存在领导者到该跟随者的一条路径。

根据线性系统理论,在假设1下,对于任何给定的正定矩阵Q,存在唯一的正定矩阵P,使得ATP+PA-PBBTP+Q=0。进一步地,在假设2下,H为正定矩阵。因此,存在一个正数l,使得lλmin(H)≥1。

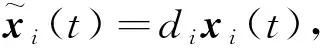
(5)

(6)

因此,有:

(7)

(8)

(9)

(10)

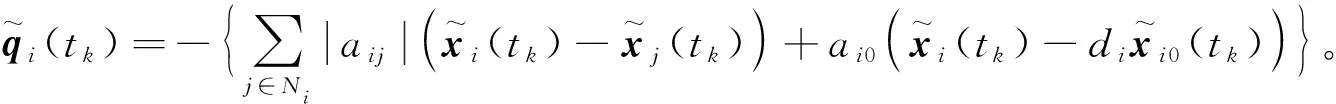
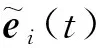
(11)

(12)

式中,控制增益为K=lBTP。

进一步设计事件触发机制如下:

(13)

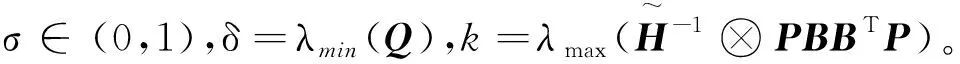
2 主要结果

首先给出两分一致跟踪的定义。

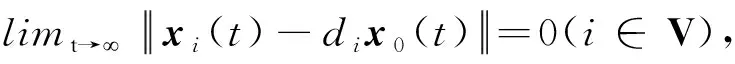
定理 由系统(1)和系统(2)组成的多智能体系统中,其控制协议形如式(9),个体间的事件触发时刻由式(13)决定。在假设1和假设2前提下,针对无向连通且结构平衡的合作竞争网络,多智能体系统可渐近实现两分一致跟踪,并且不存在Zeno现象。

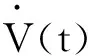
(14)

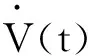
(15)

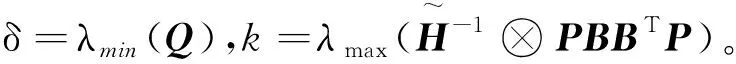
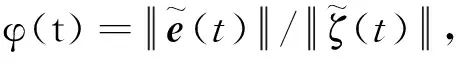
(16)

由于,

(17)

式(16)可改写为:

(18)

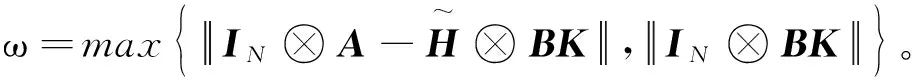
所以,有:

(19)

(20)

(21)

τ>0表明事件触发时间间隔存在正下界,也说明该事件触发机制不存在Zeno现象。证毕。

3 数值仿真

用一个具体数值仿真实例来验证定理和理论推导的正确性。

1个由7个个体组成的合作竞争网络,0代表领导者,1～6代表跟随个体,其网络拓扑结构图如图1所示,其中实线边的权重为正,表示合作关系;虚线边的权重为负,表示竞争关系。显然,合作竞争网络G1是结构平衡的,即V1={1,2,3},V2={4,5,6},进而对应的规范变换矩阵为D=diag(1,1,1,-1,-1,-1),个体1和个体5可以直接获得领导者的信息。根据图1可以得到拉普拉斯矩阵L以及矩阵H,

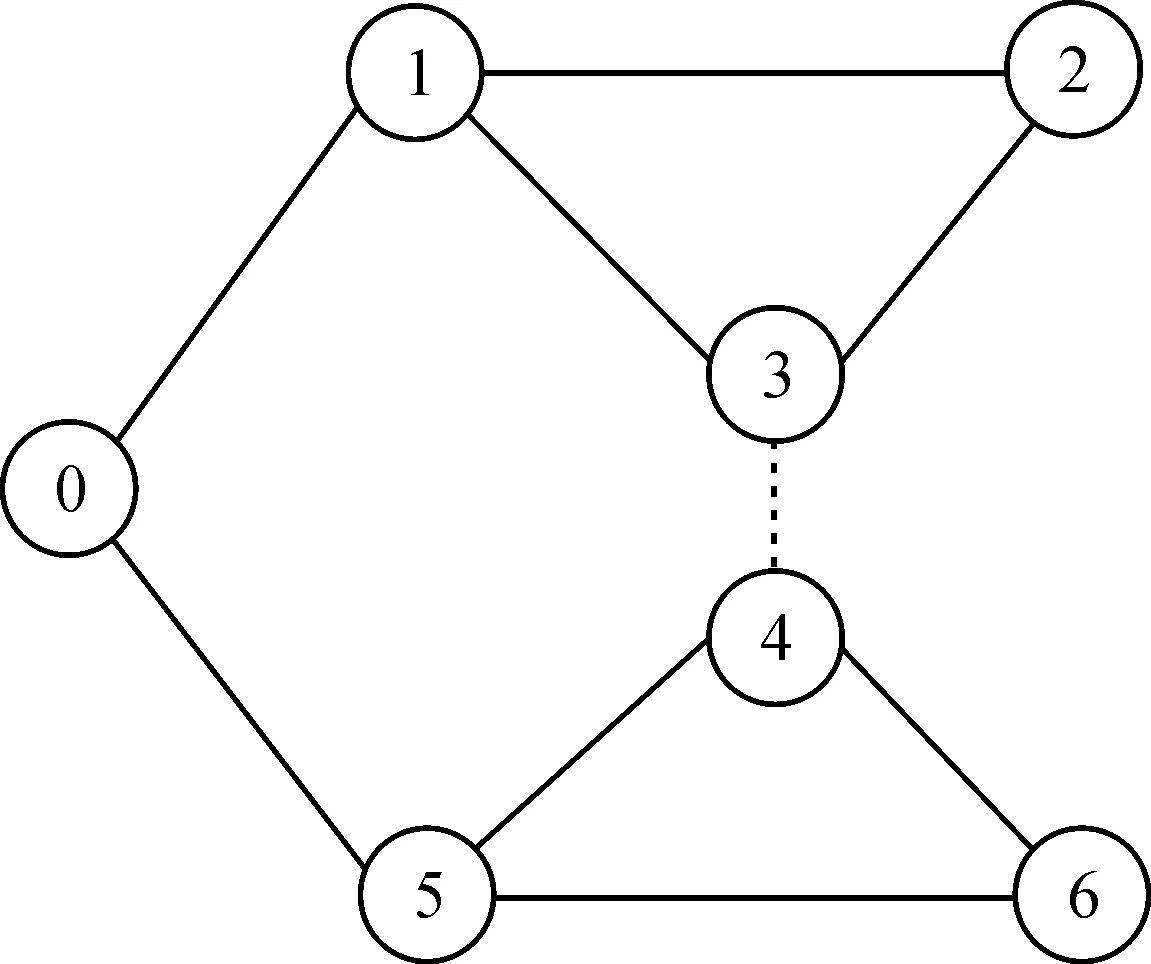
图1 通信拓扑图

多智能体系统的个体状态方程如下:

(22)

(23)

其中,取m=1,a=1,g=9.8,且

图2 集中式事件驱动的智能体状态轨迹图

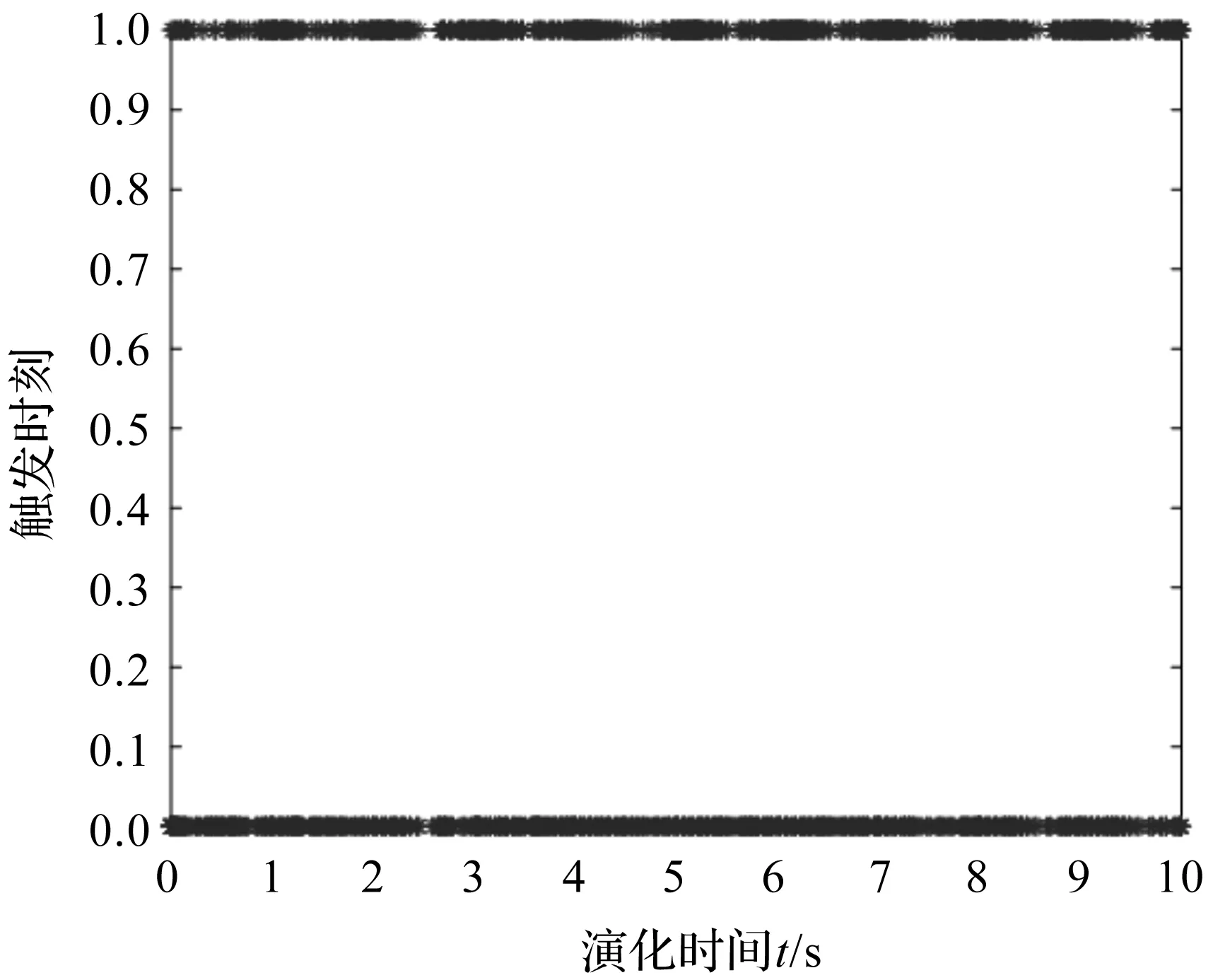
图3 集中式事件驱动的触发时刻

从图2可以看出,随着演化时间的变化,跟随者与领导者的状态最终呈现为数值相同,符号相反,实现了两分一致性跟踪的目标。从图3可以看出,智能体之间的通信次数减少,有效降低了通信成本。综上分析可知,在满足相应条件和相应控制器的情况下,合作竞争网络拓扑结构中的个体最终可渐近实现两分跟踪,验证了本文理论的正确性。

4 结束语

针对一类多智能体系统的分布式两分跟踪问题,本文设计了一类新型的带有事件触发机制的控制协议。在设计的控制协议下,无向连通且结构平衡的合作竞争网络中,所有个体状态均能渐近实现分布式两分跟踪,且不会出现Zeno现象。但是,本文设计的事件触发机制只是合作竞争网络的初步探索,研究对象是一阶线性多智能体系统,后续将对二阶系统或非线性系统展开进一步研究。