SST 湍流模型改进研究综述

曾宇，汪洪波，孙明波，王超，刘旭

国防科技大学 空天科学学院 高超声速冲压发动机技术重点实验室，长沙 410073

剪切应力输运（Shear Stress Transport，SST）模型是一个性能出色的全能型RANS（Reynolds-Averaged Navier-Stokes）模型，也是目前广泛使用的涡黏假设模型中性能评价最好的一个，因此受到模型研究者和有湍流模型使用经验者的推崇。标准SST 湍流模型的基本原理是：在近壁面处采用k-ω模型［1-2］、在边界层外区和自由剪切中使用k-ε模型［3］，并通过Bradshaw假设（在边界层中，剪切应力正比于湍动能）引入雷诺剪切应力输运的影响。因此它巧妙地结合了k-ω、k-ε以及J-K模型［4］的优点，规避了它们的缺点，能较好地处理湍流剪切应力在逆压梯度和分离边界层中的输运，以其精度高、鲁棒性好、适用性广的优势成为航空航天领域应用最为广泛的湍流模型之一。

随着计算能力的快速增长，计算流体力学（Computational Fluid Dynamics， CFD）也飞速发展，大涡模拟（Large Eddy Simulations，LES）技术和混合RANS/LES 技术等逐渐发展起来，人们可以用更精细的网格、精度更高的算法计算更多、更复杂的算例，画出更绚丽的流动图像，得到更多有用的信息。但Spalart［5］指出，这一局面可能会导致湍流建模的停滞不前。阎超［6］认为自SST 湍流模型提出的许多年里，在湍流模型核心理论方法方面没有突出的成果面世。虽然在工程上RANS 取得了巨大成就，但湍流模型仍伴随着很多未解决的问题。而且，由于LES 提供了更加丰富、直观的流场信息，研究者们更乐于通过该技术开展理论研究。这些原因可能会导致RANS 湍流模型的竞争力下降，并可能被LES 技术取代。但事实上，在计算能力上的提升不仅使RANS 的应用市场扩大了，而且RANS 分析更普遍地见于日益复杂的问题中［7］。Hanjalic［8］也认为，RANS 方法已经在工程实践中根深蒂固，将经验公式与湍流模型相结合，获得相对较高的预测精度，以及对绝大多数用户友好等，这些特点使得RANS 并没有走向消亡。在可预见的未来，湍流模型仍将是计算流体动力学分析，特别是工程研究最主要的手段［9］。

Durbin［10］在回顾湍流建模的进展中也指出，湍流建模是数值分析的关键，而RANS 建模的对象主要是-，即雷诺应力（“-”和上标“′”分别表示雷诺平均方法和脉动量）。根据建模方法的不同，主要可分为雷诺应力模型（Reynolds Stress Model， RSM）和涡黏性模型（Eddy Viscosity Model， EVM）2 类，其中又以形式简单、易于实现的线性EVM 模型在工程领域发展较快。目前，根据需额外求解的湍流输运方程数量，线性EVM 模型大致可分为零方程（例如C-S 模型［11］，B-L 模型［12］）、一方程（例如B-B 模型［13］，S-A 模型［14］）和二方程湍流模型。几十年来的湍流模型发展经验表明，不同湍流模型的发展是紧密联系的，例如：为改善混合长度模型提出了C-S湍流模型；B-L 模型又是为了改善C-S 模型中特征长度的计算；为改善零方程无法反映上游历史影响的问题提出了一方程；为改进一方程中对湍流长度尺度或时间尺度的计算从而研发了二方程。总之，湍流模型发展和改进不是一蹴而就的，借鉴不同模型的建模理念和优点普遍存在。比如与显式代数雷诺应力模型［15］（Explicit Algebraic Reynolds Stress Models， EARSMs）相结合的SST 湍流模型可以实现对二次运动、旋转/曲率的敏感化［16］。近年来，许多学者都开展了耦合不同物理现象到SST 湍流模型上的工作，丰富了对SST 的研究内容，同时取得了一定的成果，但研究也表明，大多只能从修正的角度较好地改善对应问题的预测，结果也比较单一。偶尔有耦合较好的SST 修正模型在仿真计算中取得了较好的结果，这是令人欣慰和大受鼓舞的。在未来的一段时间内，合并已发展的物理现象修正方案将是改进SST 湍流模型预测精度和应用范围的主要工作和进一步研究的问题。

本文从SST 湍流模型的角度梳理了不同学者纳入流动物理或物理现象的湍流模型改进研究，对基于SST 湍流模型框架发展的修正研究进行归纳和总结。在第1 节中介绍了标准SST 湍流模型及其能解释的物理和流动现象；第2 节阐述了在旋转/曲率、可压缩性、激波不稳定性、雷诺应力各向异性、应力-应变偏差特性和层流/湍流转捩等6 个方面中SST 湍流模型的改进与提升以及基于数据驱动技术开展的湍流模型改进；最后论述了目前的发展状态并展望了重点关注的方向。

1 标准SST 模型及其物理含义

Menter［1-2］提出的标准k-ωSST 湍流模型主要由湍动能和比耗散率2 个脉动量输运方程组成，具体表达式为

式中：ρ为密度；t为时间；k为湍动能；ω为比耗散率；β*、σk、γ、β、σω、σω2为模型常数；μ为动力学黏性；μt为湍流涡黏性；νt为湍流涡黏性系数；F1为混合函数。

其中：ui为笛卡尔坐标系下xi方向上的速度分量；τij为雷诺应力；δij为克罗内克符号。

湍流涡黏性系数νt为

式中：a1为结构参数，Menter［1-2］取值为0.31；F2为边界层混合函数。需要说明的是，式（2）中A′、B′和C′的上标“′”旨在与式（1）中A、B和C区分。

模型常数通过混合函数F1计算得到，混合方式为

式中：ϕ1为原始k-ω模型中的模型常数；ϕ2为标准k-ε模型中的模型常数；ϕ为SST 模型中的模型常数。混合只在边界层尾迹区域内进行。

混合函数F1旨在实现使用k-ω模型对近壁面湍流流动进行预测，而在远离壁面的流动中通过k-ε模型实现对自由流的捕捉。这2 种模型分别对相应的流场区域有较好的预测结果。

此外，为改善对逆压梯度流动的预测精度，在湍流边界层中还引入了雷诺应力正比于湍动能的假设，这是通过湍流涡黏性系数νt中的max函数实现的，并通过F2函数控制只在边界层中使用该假设。函数F1和F2有相似的变化规律。

建模中使用到的一些其他关系为

式中：ν为分子运动黏性系数；ymin为到壁面的最小距离。

建模中使用到的2 组常数为：①（ϕ1，Wilcox），σk1=0.85，σω1=0.5，β1=0.075，β*=0.09，κ=0.41，γ1=β1/β*-σω1κ2/；②（ϕ2，标准k-ε），σk2=1.0，σω2=0.856，β2=0.082 8，β*=0.09，κ=0.41，γ2=β2/β*-σω2κ2/。

基于SST 湍流模型框架展开的改进研究如图1 所示，近年来对这些内容的研究仍在进行，其中主要是以内容的影响开展的，而由此发展起来的修正可能会与实际流动不符合，因为绝大多数的流动都会耦合2 种或多种图示内容的影响。合理地衡量这些内容的影响，理清标准SST 湍流模型所能预测的物理现象和模型的缺陷，明确在流动中的物理机制是如何用数学表达式表达的，起主要影响作用和次要影响作用的机理该如何区分，这是研究SST 湍流模型必不可少的环节。

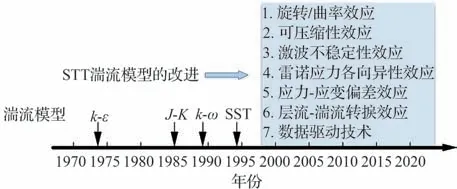
图1 SST 湍流模型主要发展历程Fig. 1 Major developments in SST turbulence model

标准SST 湍流模型对湍流运动物理现象的描述主要是通过式（1）和式（2）式实现的。首先，在不可压缩条件下，引入了Boussinesq 假设，建立起雷诺应力与平均速度应变率的线性关系：。

其次，对湍动能输运方程中的各项进行建模。式（1）中的A项：，是流体平均变形抵抗雷诺应力所做的功，表征从平均运动中输送到湍流运动中的动能，此项通常为正，起到增加湍流动能的作用，称为湍动能产生项；式（1）中的B项：，是流体抵抗脉动变形的脉动黏性应力所做的变形功，表征脉动运动引起的能量耗散，它总是消耗湍流的动能将其转化为热能，称为湍动能耗散项；式（1）中的C项：·，是由流体自然分子输运和湍流输运过程产生的湍流能量扩散，表征脉动压力、雷诺应力和脉动黏性应力对脉动能量的输送，称为湍动能扩散项。

然后，类比湍动能方程的建模，可通过Navier-Stokes 方程得到湍流脉动耗散率ε或比耗散率ω的精确方程。Kolmogorov［17］指出，流动中最普遍的几个物理过程是非定常、对流（或者平流）、扩散、耗散、散布以及产生过程，结合物理和量纲分析，给出了比耗散率输运方程的建模。经过一系列发展，最终形成了目前使用的式（2）形式，其中A′、B′和C′这3 项在表达形式和物理意义上与湍动能输运方程中的A、B、C这3 项的内容一致。

需要指出的是，式（2）中的D项：

是根据ε=β*kω的关系，将ε输运方程转换为ω方程时产生的，称为比耗散率交叉扩散项。

通过上述分析可得，标准SST 湍流模型主要描述的流动物理为

标准SST 湍流模型是在不可压缩条件下发展起来的，建模后的雷诺应力具有各向同性的性质，对具有方向性的力不敏感，一些其他行为的影响被忽略，从而获得了相对精确的SST 湍流模型，既保证了一定的流动预测能力，又具有易于实现的计算形式和较少的计算量。然而，随着计算能力的提升，应用范围的拓展，标准SST 湍流模型显现出预测能力不足的问题。由上可知，限制SST 湍流模型预测精度和应用范围的正是建模过程中的一些限定条件：比如，不可压缩流动；Boussinesq 假设的应力-应变关系；忽略了高阶脉动关联项的影响以及标定的模型常数。学者们分别从以上几点限定条件展开研究来改善湍流模型工作性能，使其具有反映应用环境的能力。

2 SST 湍流模型改进研究

近年来许多学者已经提出了切实可行的修正方案来解决SST 湍流模型对旋转/曲率效应、可压缩效应、激波效应、各向异性效应、应力-应变关系的偏差效应以及层流/湍流转捩效应预测不准的问题。虽然面临的问题对象不同，但解决问题的具体方法大体是一致的，主要可以归类为以下几种方式来改进k和ω的输运方程，从而改善对物理现象的捕捉：① 直接限定湍动能产生项；② 改进涡黏系数表达式；③ 改进雷诺应力表达式；④ 改进耗散项系数表达式；⑤ 增添脉动关联项的建模关系式；⑥ 改进常系数数值；⑦ 增加新的输运方程。这些方法或多或少提升了应用领域中关注物理量的预测精度，但这些修正是否会产生破坏其他物理量的行为仍待考察。此外，基于不同物理现象发展的修正方案能否合并耦合到SST 湍流模型中，以及合并耦合的内在机理尚未有定论。为进一步探索这些问题，现对SST 湍流模型的改进研究做一个系统的梳理。

2. 1 旋转/流线曲率效应

SST 模型是坐标不变的，很难在不修改的前提下准确地预测具有特定方向影响的流动，其中最具有代表性的是参考系旋转/弯曲壁面流动，显著增加了湍流的复杂性。许多研究人员对这些内容进行了系统研究［18-23］，指出系统旋转和流线曲率之间存在类比，2 种现象对流场的影响是一致的，故而大多以流向曲率作为研究对象。流线曲率包括2 种类型，“凸”面和“凹”面，这里术语“凸”面是指沿壁边界层的曲率中心位于表面内，另一种则相反［24-25］。Durbin［26］指出，2 种曲面中会存在2 种旋转，一种是旋转方向与剪切方向相同，旋转降低湍流强度；另一种是旋转方向与剪切方向相反，增大湍流强度。在没有旋转的情况下，Brethouwer［27］发现，湍动能k由平均切应变产生，随时间增长；但引入旋转后，可以提高或降低k的产生速率。另外，对旋转的通道研究表明，靠近一侧墙面的湍流增强，并且靠近另一侧墙面的湍流减弱，流动出现不对称［28-30］。由此可知流场在方向性力（离心力、向心力、科氏力等）的影响下，湍流中能量分配的机制会发生一定的变化，这不仅在宏观上表现出湍动能的增大或减小，在力的方面体现为雷诺应力的各向异性。

SST 湍流模型中对雷诺应力的建模是根据Boussinesq 提出的涡黏假设：τij=μt·，当i≠j时，其退化为2μtSij，这表明雷诺应力在本质上是各向同性的，但实际情况旋转/流线曲率引起的影响是特定方向上的，这会使得雷诺应力在不同的方向上有不一样的表达，从而呈现出明显的各向异性特征，然而该表达式无法复现这一特征。除此之外，SST 模型求解的是2 个标量k和ω的输运方程。这使得旋转/曲率引起的这些效应不会被各向同性的、标量的、对旋转/曲率不敏感的SST 涡黏模型捕捉到。Menter［2］和Wilcox［31］对如何将物理现象或影响效应纳入到湍流模型中去给出了指导，工程湍流建模在强调理论概念的同时，也应注重该学科的经验性质，湍流模型要求的是对流动物理的建模而不是对其微分方程进行建模。

曲率效应作用到湍流中的宏观表现是增强或抑制湍流强度，即促进或抑制k的产生，这也就是说在SST 模型基本框架不变的前提下，这一影响可以通过一定的方法耦合到k和ω的输运方程中。另一个角度是从力的影响来考虑的，旋转/曲率主要是改变了雷诺应力的表达，进而影响了能量分配和传递过程。Huang 等［23］综述了旋转/曲率的影响，指出这些效应可以通过将模型常数参数化，以实现抑制或增加湍流动能的增长速率或者将涡黏系数参数化来实现曲率效应。主要是在湍流模型方程式（1）和式（2）中的A、B、A′和B′这4 项上展开修正，或者引入额外的输运方程，从而使改进后的SST 模型对旋转/曲率敏感。需要指出的是，在保持SST 模型框架不变的前提下，额外的输运方程是通过中间参数来影响k和ω输运方程中A、B、A′和B′这4 项的表达，从而达到旋转/曲率修正的效果。

2.1.1 对输运方程中特定项的修正

Spalart 和Shur［32］指出，在均匀旋转剪切流和弱曲率/旋转的2 种极端类型的剪切流动中，前者的强旋转抵消了雷诺应力的效果，而后者雷诺应力水平有相当大的变化，通过比较涡量和应变速率的大小可以得到衡量旋转/曲率效应的伽利略不变量度。在不稳定的旋转/曲率影响下，应变率S会超过涡量Ω，反之亦然。由此提出可以设计基于S/Ω比值的经验修正，并在S-A 湍流模型［14］上给出了一种基于比值S/Ω的、经验主义的旋转/曲率修正方案，即在湍流模型方程中的产生项上乘以“旋转”函数fr1，其表达式为

其中：

式中：DSij/Dt为应变张量的拉格朗日导数；为参考系的旋转角速度；ξijk为符号函数。

修正后的S-A 模型在较宽范围的旋转/曲率流中获得了更精确的结果［33］，这激发了Smirnov和Menter［34］将这种修正方法应用到SST 模型当中的兴趣，对拓展到SST 模型的曲率修正函数做了适当的修改，然后通过它控制SST 模型中湍动能的产生和比耗散率的生成行为，曲率修正后的SST 模型为

曲率修正函数的下限为0，表征强凸曲率稳定流动情形（无湍流产生）；上限表征强凹曲率情形（湍流增强），1.25 为文献［34］中给出的最佳经验常数值。

应用到SST 中需要的一些修改为

式中：D2=max(S2，0.09ω2)；cr1=cr3=1，cr2=2。

修正后的SST 湍流模型显著提高了捕捉旋转引起的非对称速度分布的能力和预测精度，与直接数值模拟（Direct Numerical Simulation，DNS）和RSM 模型的结果对比表明，修正后的SST 模型具有相当的竞争力，且计算成本显著低于RSM。但就实现而言，在求解r͂中使用了应变率张量的导数，而这在代码中实现十分复杂。Musa 等［35］对此做了改进，将r͂的求解式变为

在U 形管道中测试了改进后的r͂，结果表明能一样有效地预测旋转/曲率效应，并且需要较少的计算量［36］。

此外，Bradshaw［37］研究了Richardson 数与旋转/曲率影响之间的关系，指出这两者之间存在相似的特征，并提出用Richardson 数来表达曲率的影响的建议。经过长期发展，提出了许多依赖Richardson 数的旋转/曲率影响方法，将影响归入到对湍流长度尺度变化的修正［38-40］，具体的表达式为

式中：l为湍流长度尺度；l0为零旋转时的混合长度；Crc为旋转/曲率敏感常数系数；Ri为Richardson 数。

根据湍流涡黏性μt与湍流长度尺度l成正比，可以直接在涡黏性表达式上乘以湍流长度尺度变化的修正公式。然而，在双方程湍流模型中，对输运方程中一个或多个湍流源项的系数进行修正更有吸引力，其中又以对耗散率方程/比耗散率方程的耗散项进行修正较为普遍。Hellsten［41］将旋转/曲率效应归入到SST 模型中k方程的耗散项上，通过改变耗散行为从而间接影响湍动能的表达。修正后的比耗散率输运方程为

给出的修正公式为

Richardson 数的广义定义为

由Ri的表达式可知，当Ω/S=1/2，Ri有最小值-1/4。如果曲率足够强（Ri＞0），函数F4会降低B′modified项，从而增加ω的增长率，这表明曲率对湍流的抑制。研究结果表明了修正后的SST 湍流模型在旋转数低于0.1 时与展向旋转通道流和凸曲面边界层流动实验结果更吻合的预测，但在凹曲面壁流动和旋转圆柱体的轴向流动中是否具有更好的预测能力仍需进一步评估。

任芸等［42］在SST 湍流模型上结合了Spalart和Shur［32］以及Hellsten［41］提出的旋转/曲率修正方法，同时对式（1）中的A项和式（2）中的A′项和B′项引入旋转/曲率敏感化修正。这种直接结合的修正方法为湍流模型的研究提供了参考，但这种结合的内在联系没有得到进一步的阐述。

旋转湍流的稳定性是一个经典问题，稳定性的程度与旋转的强弱有关，其中“稳定”指的是湍流动能的衰减，“不稳定”指的是湍流动能的增长［43-44］。从稳定性的角度，Reif 等［45］提出，如果湍流模型能够捕获从不稳定到稳定的分岔，或者捕获从稳定到不稳定的分岔，则认为模型能够反映局部旋转效应，并将这种方法称为“分岔法”。Arolla 和Durbin［46］通过对“分岔法”的理解，提出在比耗散率方程中的产生项上乘以旋转/曲率效应乘法因子的修正模型，乘法因子为

式中：α1=-0.2。

修正SST 模型的ω方程为

在测试案例中对该模型进行了测试，并比较了基于“分岔法”的修正和其他修正系数的方法，结果表明该模型得到的结果是令人鼓舞的。

Huang 等［23］指出，直接在输运方程的产生行为和耗散行为上引入旋转/曲率的修正所能实现的改进是有限的，值得注意的是，旋转/曲率通过雷诺应力影响平均流动，而雷诺应力受应变率张量影响，其中切向雷诺应力（偏雷诺应力）与应变率张量线性相关，因此，一种可能的方法是修改涡黏性μt来将旋转效应纳入模型。

2.1.2 对涡黏性表达式的改进

Reif 等［45］在EARSM［47］解的指导下，通过对涡黏性进行修正来考虑近壁面湍流中的曲率效应，涡黏性系数可以写为

式中：Cμ为模型系数，一般为0.09；f(k，ε，ω，…)为流场输运量的函数，由湍流模型决定。

若通过涡黏性实现对旋转/曲率敏感化，一般情况下，使Cμ对旋转/曲率敏感更方便。Reif等［45］采用椭圆松弛建模方法来考虑靠近壁面效应，给出修正的模型系数为

在非旋转/曲率流动条件下，该修正公式会自动简化为原始的标量形式。

Arolla 和Durbin［46］直接将Reif 等［45］提出的方法拓展到SST 模型上，涡黏系数的表达为

为保证数值稳定性，给定了修正涡黏系数的上限值为2.5。再通过对的理解和分析，又推出了更简洁的涡黏系数修正公式：

显式代数雷诺应力湍流模型对旋转/曲率是敏感的。York 等［48］采用广义EARSM 的解来计算雷诺应力的各向异性张量，由此给出对旋转/曲率的修正：

式中：K1～K8为模型常数；W为旋转项，计算式为

而W常采用经验公式，表达式为

Dhakal 和Walters［49］将York 等［48］对旋转/曲率的修正直接应用到SST 模型上，对标准SST模型中的涡黏性系数表达式进行转换：νt=，然后用替代其中的Cμ。结果表明该修正方法相较于标准SST 模型能更好地取得与实验和LES 数据的一致性，但也会存在高估旋转/曲率引起的湍流抑制以及低估湍流增强的现象。

2.1.3 增加输运方程

受旋转/曲率影响的湍流是高度各向异性的，而SST 模型的基础是涡黏假设，本质上不具备反映雷诺应力各向异性的能力。发展对旋转/曲率敏感化最合适的起点是对雷诺应力各向异性张量的输运方程进行理解和分析，如EARSM和RSM 模型，然后通过对这些模型做合理的简化，可以得到满足应用需要的简化模型，其优点在于该简化模型也能一定程度上呈现雷诺应力本身的特性，从而能够更好地预测流场信息。除了上述这些方法外，通过增加新的输运方程来衡量旋转/曲率效应的修正方案是合理的，这里新增的输运变量主要是用来描述流动的各向异性特征。

Durbin［50］提出的一个新变量为ν2，表示垂直于流线的湍流应力，并给出了这一变量的输运方程为

受这一模型的启发，Dhakal 和Walters［51］提出了对旋转和曲率敏感的三方程模型，对涡黏性系数的定义为

ν2的输运方程为

λ的表达式为

式中：x=2(1-W/S)/9。相关参数含义可参考文献［50］。

可以把ν2=λ2k作为旋转效果的判断变量，当λ=1 时，涡黏性系数就恢复到标准SST 模型，当λ＜1 时，旋转/曲率修正生效。

图2［51］展示了在旋转管道流中不同修正模型对湍动能分布的预测结果，其中纵坐标k*已采用平均壁面摩擦速度的平方进行归一化。通过对比可知，三方程的SST 模型预测精度更好，这在于该模型结合了旋转校正和各向异性输运方程，对存在系统旋转/曲线曲率的流场的预测精度进一步提高。同样地，其他修正也取得了正确的预测趋势。

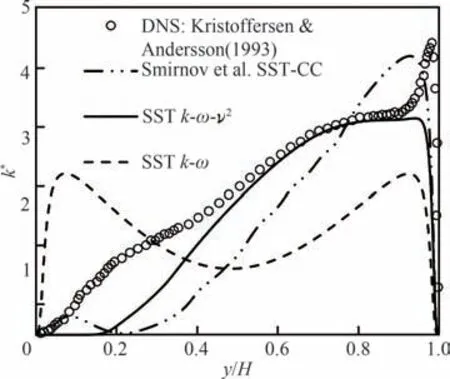
图2 旋转通道流湍动能剖面［51］Fig. 2 Turbulent kinetic energy profile of rotating channel flow［51］

通过上述的分析可知，从不同的角度，使用不同的修正方法都能一定程度地提高SST 湍流模型在旋转/曲率中的预测精度，而最具有发展前景的方向可能是突破Boussinesq 假设本身的桎梏，使雷诺应力尽可能地呈现出各向异性的能力，逐渐趋于雷诺应力本身的特性。RSM 和EARSM 模型是目前最趋于雷诺应力本身性质的湍流模型，而从宏观上控制湍动能或比耗散率的产生行为或耗散行为的修正方法要比从力的角度给出的修正方案表现出较差的预测性能。然而具有发展前景的是分岔模型和三方程模型，两者都借鉴了EARSM 的求解方法和发展思路，这是使得修正后的SST 模型具有更好预测精度和更广泛预测范围的主要原因。此外，直接将涡黏性扩展到应变率的二阶关系式或更高阶的关系式，从而使雷诺应力可以表现出各向异性的特征，也可以实现对旋转/曲率效应的捕捉。

2. 2 可压缩效应

压力波动会导致流体单元体积波动的湍流称为可压缩湍流，进而通过速度、温度和密度的脉动，影响湍流平均运动［52］。Morkovin［53］研究了来流马赫数＜5 的超声速平板边界层，并提出了Morkovin 假说：脉动密度的均方根相对于平均密度较小时，密度可以看作是一个被动标量，可压缩湍流边界层的结构与不可压缩湍流边界层的结构是相似的。Gatski 和Erlebacher［54］和Pirozzoli 等［55］也表明来流马赫数＜5 时，可压缩湍流和不可压缩湍流大部分特性差异较小，可压缩效应可以忽略不计。Bradshaw［56］讨论了湍流模型是否需要修正，指出不可压湍流模型仍然是一个很好的基础，甚至可以直接使用。基于这些研究，Morkovin 假说被应用于大多数工程可压缩壁面湍流的计算，比如SST 湍流模型直接通过计及密度的影响而应用到可压缩流动。

Coleman 等［57］指出可压缩效应对于可压缩湍流2 个方面的影响：① 当流场Ma＜5 时，可压缩效应主要影响平均量；② 压缩效应会影响到流场中热力学量（压力、密度和温度等）的脉动。在第1 种情况下，Morkovin 假说在边界层中较好地成立；在第2 种情况下，流体的可压缩性会引起湍流结构及湍流动力学特性的变化，不能使用Morkovin 假说。基于不可压缩条件发展起来的SST 模型并不能正确反映这些变化，必须对其改进，纳入可压缩效应的影响。为了更好地理清楚可压缩对流场的影响机制，Wilcox［58］、Sarkar［59］和Zeman［60］在模拟高速流动中对流体的可压缩性影响方面进行了探索性研究，认为由于压缩或扩张作用引起的湍动能和热能之间的交换是影响可压缩湍流的重要因素。可压缩湍流中平均内能、平均动能和湍动能之间能量传递方式如图3［52］所示，图中平均动能、平均内能和湍动能之间的交换通过细箭头所示的项进行，该图清晰地展示了能量与能量之间是通过哪些量直接影响的。

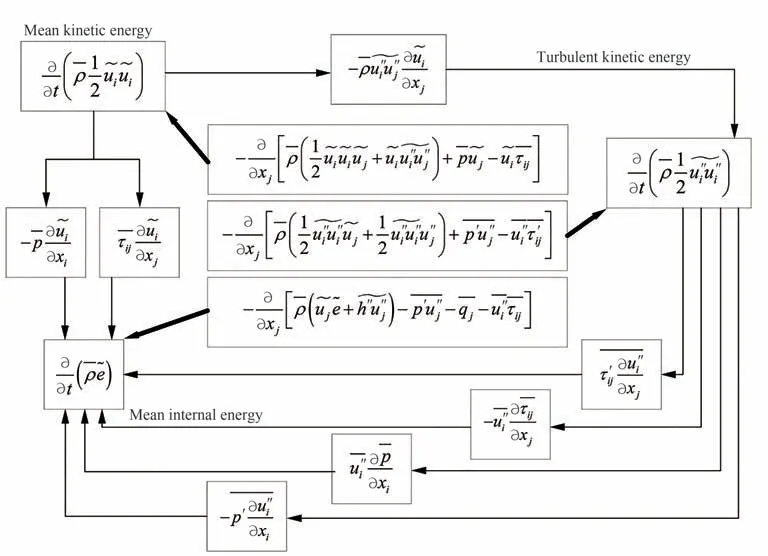
图3 可压缩湍流的能量平衡［52］Fig. 3 Balance of energy in compressible turbulent flow［52］

对可压缩湍流流动一般采用Favre 质量加权平均方法进行处理。在可压缩条件下，密度ρ不再为常数，Favre 平均的湍动能方程相对不可压缩条件下的湍动能方程主要变化在式（9）中的B″、E和F这3 项。E项和F项是由于体积膨胀而多出来的项，其中前者为脉动压力与脉动速度散度的相关项（即压力膨胀项），后者为脉动湍流质量通量与压力的相关项（压力做功项）［61］；B″项为采用Favre 平均方法而导致的可压缩性耗散率。三大守恒方程在2 种情况下是相似的。

式中：P为Favre 平均的压力；“～”表示Favre 平均；。

然而，SST 湍流模型是在不可压缩条件下由近壁面湍流模型k-ω和自由流湍流模型k-ε组成，现在要使SST 湍流模型具备可压缩效应的捕捉能力，那么按照上面的分析可知，可压缩条件下SST 模型中的k-ω模型在Ma＜5 的条件下变化不大，具有不可压的特性；在Ma＞5 时，应该能考虑边界层流场结构的变化；而k-ε模型则应该很好地反映流场中各脉动量的可压缩效应。除此之外，可压缩修正后的SST 模型还应该能反映可压缩下湍动能和热能之间的传递行为。

基于以上这些分析，下面将主要从考虑可压缩效应后模型方程中新增的项以及流场结构的变化等方面进行阐述，同时给出考虑这些可压缩效应后的SST 湍流模型的主要变化，及其在预测能力上的改变。

2.2.1 湍动能耗散率修正

通过上述分析可知，在输运方程k、ω以及ε等其中任意一方上的可压缩改进在理论上都可以被借鉴并引入SST 中。Sarkar［59］和Zeman［60］通过对可压缩流的DNS 分析指出可压缩性对湍流流场的影响是耗散的。

这里忽略了一些高阶项。再令

进一步变换得到

一般而言，

这一关系式在均匀湍流中是准确的，在高雷诺数、非均匀湍流中也是一个很好的近似。

无散度耗散率是由能量级串过程引起的，且在各向同性湍流中只与脉动涡量的平方有关，通常认为该项不受可压缩性影响，它可以被认为是等效的“不可压缩”耗散率，即。

而膨胀耗散率与脉动速度的散度有关，只在可压缩湍流中出现。

Zeman［62］假设可压缩湍流流场中存在涡旋激波，这些涡旋激波直接影响膨胀耗散率，而不影响无散度耗散率。再对照实验和DNS 结果的分析，给出了表征可压缩效应的无量纲参数，湍流马赫数Mat为

式中：c为当地声速。

湍流马赫数表征湍流波动信息传播速度与声传播速度的比值，这里湍动能反映了湍流波动传递信息的特征速度尺度。

基于湍流马赫数对膨胀耗散率εd建模：

式中：γ为比热比。

Sarkar［59］考虑了湍流波动在声学时间尺度上的演化，表明可压缩性的变化对耗散率的无散度分量的影响相对于对膨胀分量的影响可以忽略不计。还观察到膨胀耗散率与无散度耗散率之比与湍流马赫数的平方有关。基于对声波时间尺度上涨落演化的分析，给出的膨胀耗散率模型为

Wilcox［31］指出上述膨胀可压缩修正都能很好地预测混合层的增长速度，但都不能准确地预测壁面边界层情况下表面摩擦系数的变化。这表明流场的可压缩效应在不同的区域可能是不同的，即在流场中间或远离壁面区域的可压缩机制，与近壁面边界层的可压缩机制存在差异，而这种差异不能仅仅反映在湍流马赫数数值的变化上。

El Baz 和Launder［63］没有给出εd的具体表达式，但从对不可压缩模型进行可压缩修正的角度提出了一种修正，以解释由于压缩效应而产生的额外耗散率，并选择ε输运方程中耗散项的模型常数进行修改，以此来匹配观测到的可压缩各向同性湍流的衰减率。这个常数修改为

有了上述工作，Wilcox［64］根据耗散率ε与比耗散率ω之间的转换关系ε=β*kω，对其变换后有

这表明可压缩效应在k和ω输运方程中是同时存在的。基于Sarkar［59］和Zeman［62］对膨胀压缩性修正的工作，Wilcox［64］改进了输运方程中耗散项的常数系数β和β*，使其随湍流马赫数变化：

通过上述可知，一是找出无散度耗散率εs和膨胀耗散率εd之间的关系，从而在湍流模型中纳入膨胀耗散的影响；二是直接修正输运方程中耗散项的系数来引入可压缩膨胀耗散效应。虽然采用的方式不同，但最终体现在湍流模型方程上的修正方式却是类似的，即在无散度耗散率项前乘以表征可压缩膨胀耗散效应的函数，改变耗散项的表达，达到纳入可压缩膨胀耗散效应影响的目的。

Erdem 和Kontis［65］类比k-ω湍流模型与SST模型有相似的结构，直接将Wilcox［64］对膨胀耗散率的修正方法引入SST 模型中。可压缩性参与了湍动能方程中的耗散项和比耗散率方程中的耗散项。引入膨胀耗散影响的SST 湍流模型为

结果表明，在较宽的压力比范围内，该方法与实验数据吻合较好，具有一定的预测精度。

Wilcox［64］在函数F(Mat)中使用了Mat0，这是为了在湍流马赫数较高的可压缩自由剪切层中膨胀可压缩修正生效，而在趋于湍流马赫数较低的边界层近壁面区域不生效。Brown［66］发现对于马赫数＞5 的湍流边界层，湍流马赫数很容易超过Mat0值，这导致了高马赫数湍流边界层的表面摩擦和换热显著减小。为了对马赫数＞5 的情况也能使用这种可压缩性校正，重新定义湍流马赫数为

通过这一修正，可以实现可压缩膨胀率修正只应用在近壁面区域湍流边界层的外部区域而无需考虑湍流马赫数。Tu 等［67］评估了这种修正，并表明湍流马赫数的修正使分离区域比标准SST 模型略小。

Suzen 和Hoffmann［68］将膨胀耗散的可压缩效应同时引入SST 模型中，但同时也考虑了压力膨胀的效应（式（9）中的F项），可压缩效应主要在SST 模型中的k-ε方程上进行，然后通过混合函数F1将这些影响引入SST 模型中。

可压缩修正后的SST 模型为

式（13）采用了Sarkar［59］提出的压力膨胀耗散率模化方法：

修正后的SST 模型包括了可压缩耗散和压力膨胀的影响。Tu 等［67］指出同时考虑膨胀耗散和压力膨胀修正会导致预测的分离区域比实验测量的大，与标准SST 模型的预测结果对比表现出更差的预测精度。

康宏琳［69］也在标准SST 模型的框架上给出了结合式（9）中B″、E和F这3 项可压缩修正的湍流模型，旨在准确模拟高超声速湍流流动，在这种流动中基于不可压缩条件发展的湍流模型已不再适用。

这些方法都旨在实现根据流场中局部湍流马赫数信息来判断在哪些区域引入膨胀可压缩效应修正，从而改善湍流模型对流场结构捕捉精度的目的。

2.2.2 压力膨胀项修正

式（9）中的E项为压力膨胀项，是由于压力波动而同时引起的体积波动所产生的功。它可以是正的，也可以是负的，为负数的情况下表示额外的耗散［59，62-63］。

Fujiwara 和Arakawa［70］对可压缩各向同性和均匀剪切湍流的DNS 数据研究发现，压力波动和膨胀两者的相关性可以用湍流雷诺数和湍流动能产生与耗散率之比的影响来表征。Sarkar［59］对衰减的可压缩湍流和均质剪切湍流中的压力膨胀相关性演化进行了分析，建立了压力波动的泊松方程，考虑压力波动不可压缩部分和可压缩部分的演化，并将压力波动分解为快速变化部分和缓慢变化部分，基于不可压缩湍流中压力-应变关系的建模思想，提出了对压力膨胀项的修正：

Zeman［62］根据压力波动方差的输运方程的平衡，也给出了压力膨胀项的模化公式：

式中：相关参数含义可参考文献［62］。

El Baz［71］提出的修正主要是基于不可压缩流动中压力-应变相关项的模型，可压缩性的变化是通过引入一个常数来实现的，这个常数被认为是可压缩性的一个本征函数，在不可压缩极限时其值为零。由此得到了压力膨胀项的模型为

Shyy 和Krishnamurty［61］指出Sarkar［59］模型以及El Baz［71］的模型都是用于混合层的，当将其应用于边界层时，它们会降低湍动能的水平，这是一个不希望出现的结果；Zeman［62］提出的模型改善了边界层中对数层分布规律的预测。

压力膨胀修正也表明，可压缩效应在流场的不同区域表现出不同的物理行为，基于混合层发展的压力膨胀修正模型应用于壁面边界层时不能提高预测精度。然而目前的修正方案还无法根据修正公式严格地区分这些。

2.2.3 压力做功项修正

双方程模型在不可压缩流体中成功的原因之一是，除了εs或ω输运方程外，所有其他方程都是精确输运方程的模型形式。对于可压缩流动，湍动能方程经过Favre 变换后，除了上述2 处不同之外，还有式（9）中的F项，其是湍流质量通量与压力梯度之间的相关项，这一项的未知量是湍流质量通量，表明可压缩性的影响是通过密度变化来实现的。此外，湍流质量通量似乎也是非均匀可压缩湍流的基础，因为其表征平均密度梯度的影响，可以类比各向异性张量表征的是平均速度梯度的影响。

Ristorcelli［74］指出，除非存在较大的密度梯度，否则质量通量对常见的单向剪切流（如平板边界层和各种自由剪切层）的贡献不大。预计质量通量项在更复杂的流动中是重要的：这些流动包括由于高马赫数或燃烧、分离或再附着（拐点）、冷壁面边界条件、平均膨胀、冲击、逆压梯度或在斜坡型流动中发生的强流向流动。因此，提出了对湍流质量通量的可压缩修正方法，试图通过湍流质量通量模型来引入压力做功项对湍流增强或减弱的影响。

Gaviglio 等［75］在实验中观察到的总焓不变是成立的。基于这一点，Krishnamurty 和Shyy［72］假定滞止焓是不变的，由此推导出了湍流质量通量的表达式为

式中：相关变量含义可参考文献［75］。

Rubesin［76］特别引入了关于波动焓的假设，并要求规定一个多变常数，提出对质量通量的模化为

式中：相关变量含义可参考文献［76］。

Ristorcelli［74］对质量通量的建模进行了回顾，通过推导湍流质量通量的演化方程，得到质量通量与平均密度梯度成正比的结论。Chassaing［77］在对可变密度湍流的回顾中给出了对质量通量的模型：

刘景源［78］研究了上述可压缩修正的SST 模型与标准SST 模型在高超声速绕流中的表现，表明可压缩修正后的SST 模型具有更高的预测精度。甘文彪等［79］在分离流动中使用了可压缩修正的SST 模型，表明适当的可压缩修正能改善超声速和高超声速分离流动的预测。

2.2.4 其他可压缩性修正

针对在可压缩条件下湍动能输运方程新增项的建模工作已经有很多，并取得了一定的成果，但将全部的可压缩修正方案统一应用于流动计算中，并且取得较好结果的公开资料却很少。基于不同物理假设发展起来的可压缩修正模型耦合应用仍然需进一步探索和研究。2.2.1～2.2.3 节的内容阐述了在可压缩条件下湍动能k方程中新增的膨胀耗散率部分、压力膨胀部分和压力做功部分，在理论上给出了精确的湍动能方程，并对其新增的部分给出了合适的建模方法，使得湍动能方程尽可能多地涵盖了流场的信息。然而双方程输运模型以及其中的SST 湍流模型除了包含有湍动能方程外，还有比耗散率ω输运方程或耗散率ε（ε=β*kω）输运方程。通过Navier-Stokes 方程和湍动能方程可推导ε精确的输运方程，并且研究表明，可压缩下的ε方程与不可压下的有所不同，这一点与湍动能方程是一致的，即也会出现类似湍动能方程一样的可压缩效应。

Krishnamurty 和Shyy［72］认为精确的耗散率输运方程在考虑可压缩效应后，会像湍动能方程一样出现一些具有可压缩特征的项，并将这与无散度耗散率输运方程形式不同的项称之为斜压扭矩影响的项（Bε），这是由压力梯度和密度梯度方向不同而产生的产生项。εs输运方程通常遵循不可压缩形式，从而忽略了斜压扭矩的影响。而缺乏Bε的影响可能是造成计算不准确的原因之一，故对Bε进行了模化，并将其加入到无散度耗散率 输运方程中以考虑这一影响。Bε的模化形式为

式中：Cε1=1.43，需要指出的是没有实验数据或DNS 数据来指导选择这个常数。

除此之外，随着马赫数的增加，流场的结构也会有所变化。基于不可压缩条件发展起来的可压缩湍流模型认为流场结构的变化不大，并认为不需要特意考虑这一影响。正如Morkovin［53］指出的，在马赫数＜5 的情况下，可压缩湍流边界层的结构与不可压缩湍流边界层的结构是相似的。但这也意味着马赫数越大边界层的流场结构存在改变的可能性，而自由流区域更有可能。为了提高预测精度，在湍流模型中引入结构变化的影响也是必不可少的。

Sarkar［80］较早地研究了可压缩流动下流场结构是否会发生变化的问题，观测表明可压缩性会极大地减少湍动能的再分配行为。研究发现梯度马赫数可以很好地作为一个无量纲参数来衡量可压缩对流场结构的影响，梯度马赫数为

式中：l为湍流长度尺度；c为声速。

最初最具代表性的结构压缩效应模型，是由Heinz［81］提出的，通过对的值与湍动能产生率和耗散率比值的研究，对k-ε模型中的常数Cμ进行了修正，使其随梯度马赫数进行变化来引入可压缩对流场结构的影响，这也就是说常数Cμ可以表征为流场的结构参数：

而当梯度马赫数为0 时，系数的值与不可压下的常数值0.09 不一致，因此Niu 和Hou［82］将其改进为

Cμ和SST 模型中的系数β*是一致的，将上述修正应用到SST 模型当中去，只要进行替换。

韩省思［83］指出通过Cμ=0.09exp (-0.4Mag)表征的结构可压缩修正来计算耦合的湍流涡黏性μt可能会产生较大的误差甚至错误的结果，为解决这一问题，引入了Durbin［84］提出的涡黏性可实现性限定来保证其在正确的范围，限定式为

此外，SST 模型中在近壁面区域内采用的是Bradshaw 的假设，即湍流边界层中的主湍流应力与湍流动能成正比，由此引入了结构参数a1，并取值0.31，这是基于不可压缩平衡边界层数据。值得注意的是，可压缩零压力梯度边界层的结构参数也表现出相似的值［85-86］。而对于非平衡可压缩流，结构参数值需要增大才能获得更好的预测结果。刘景源［87］指出SST 湍流模型引入的结构参数a1在高超声速绕流中并不成立。一些研究者在使用标准SST 模型研究激波不稳定现象中也指出，Menter［2］校准的结构参数a1在预测激波诱导分离中有较大的影响。Georgiadis 和Yoder［88］在激波/湍流边界层相互干扰（Shock Wave/Turbulent Boundary Layer Interaction， SWTBLI）的流动中研究了0.31 ≤a1≤0.4 范围内结构参数a1的影响规律，表明涡黏系数限制器中结构参数在预测雷诺应力中确实存在重要影响，将a1提升到0.355 附近，可以显著提高激波与湍流边界层相互作用的分离流预测精度，如表1［88］所示实验数据和SST 模型对分离程度的测量结果。Evans 和Lardeau［89］进一步指出将结构参数a1提高到0.355，它可以完全消除SST 模型中涡黏系数限制器本身的任何影响，但在许多复杂的流动配置中得到了很大的改善，在复杂的流动结构中，将a1增加到至少0.36 可得到更稳定的解。总体而言，标准SST 湍流模型中的结构参数a1在很大程度上高估了分离区域的湍流黏度比，同时也低估了回流区域的湍流黏度比，而通过改变结构参数的值可以实现更好的预测精度。

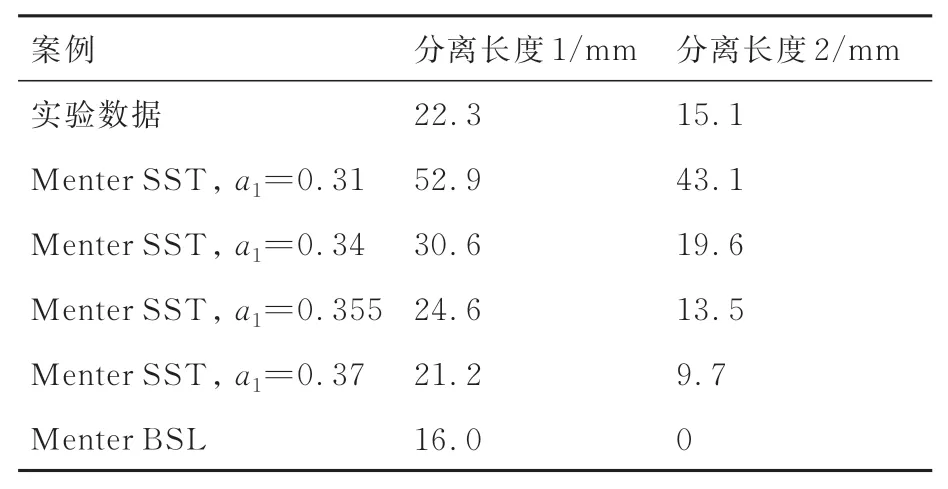
表1 在Ma=2.25 的UFAST SWTBLI 算例中实验与不同a1值的SST 模型对分离程度的测量结果［88］Table 1 Measurement results of separation extent for experiment and SST model with different a1 in UFAST SWTBLI of Ma=2.25［88］

通过以上的研究可知，可压缩效应的影响随着马赫数的增加而不断增强，虽然应用不可压缩条件发展的湍流模型能取得一定精度的计算结果，但完备的可压缩模型在理论上是更完备的。针对可压缩效应的脉动关联项以及流场结构的变化等开展了工作，得出了一些有意义的结论，可压缩性是区域性的，但单独使用基于湍流马赫数或梯度马赫数发展的可压缩机理还不能很好地表征可压缩效应，直接耦合不同的可压缩修正也难以取得更好的预测精度，这可能在于可压缩下建模的脉动关联项在本质上也是流动物理的产生行为、耗散行为和扩散行为中的一部分。

2. 3 激波不稳定性效应

无论是膨胀可压缩性修正还是结构可压缩性修正，均是在可压缩混合层这一基本自由发展的湍流流动研究中发展来的，而本节的出发点旨在将激波/湍流边界层相互作用这一基本物理现象对流场的影响纳入湍流模型中。

过去几十年通过压缩角、膨胀压缩角、正激波和斜激波等装置［90-92］对SWTBLI 做了广泛的研究，在高速环境中激波与湍流边界层之间的耦合非常强，常伴随着边界层分离和激波低频脉动现象。流动分离常常与逆压梯度相统一，而对于产生激波低频不稳定现象的机理仍没有完全统一。在激波与均匀各向同性湍流、均匀剪切湍流、湍流射流、剪切层、湍流尾流等相互作用研究的回顾中可知［93-97］，激波区域中的湍流特征速度、时间和长度尺度发生了很大的变化，而这取决于激波的强度、方向、位置和形状，以及流动几何形状和边界条件，但速度波动的放大和长度尺度的实质性变化是激波/湍流边界层相互作用最本质的结果。

张昊元等［98］研究了SST 模型中湍动能k忽略对RANS 方程的影响，指出部分湍动能项的忽略会改变有效平均压力场，从而影响分离点附近的逆压梯度，使得流动分离区范围大幅度变化。Clemens 和Narayanaswamy［96］提出剪切层卷吸再补给机制来描述激波的低频脉动，认为上游边界层波动似乎是扰动的一个重要来源，且影响随着分离流尺寸的增大而减小。此外，范孝华等［99］就激波低频非定常性的几种物理机制做了评述，指出不同的物理机制都在一定程度上提及了上游/下游机制的综合作用，表明调和上游/下游机制之间的争论，对于解决SWTBLI 低频非定常性的驱动机制具有较大潜力。程剑锐等［100］构建了一种新的弯曲激波/边界层干扰理论体系，将流场划分为弯曲激波/膨胀波干扰区、弯曲激波/分离激波干扰区和边界层流动分离区3 个典型流动区域。这些工作为更好地将激波/湍流边界层干扰流动物理纳入湍流模型中奠定了基础。

2010 年AIAA 的SWTBLI 研讨会报告指出，湍流模型对激波/湍流边界层相互作用预测的影响与网格的影响一样强烈［101］。Vieira 和Azevedo［102］比较了不同湍流模型的预测能力，指出相较于其他涡黏模型，SST 湍流模型在大多数SWTBLI 情况下显示了更好的结果。EARSM和RSM 是可以改善结果的替代方案［103］。

尽管标准SST 湍流模型在预测激波/湍流边界层的相互干扰中整体表现出较好的结果，但其计算的平均激波厚度比实验中观察到的更小，这在于激波不稳定性导致激波平均厚度远远大于稳态激波的平均厚度，而标准SST 模型并没有考虑这一物理现象。此外，激波厚度还取决于计算的数值格式和激波附近网格的分辨率［101］。Sinha等［104］指出计算的激波变薄，会使得湍动能和无散度耗散率的放大量迅速增加，而这是由于产生项和压力膨胀项与激波厚度倒数相关的非物理变化导致，通过对相关工作的归纳整理，认为原来的涡流黏度假设在通过激波的高度非平衡流中失效，但通过等式，将涡黏性μt设为0，能获得更精确的湍动能k。进一步指出，非定常激波运动会抑制k在激波区域中的放大，并建议通过抑制激波区域内湍流动能产生项或涡黏系数从一定程度上衡量激波不稳定性效应。根据线性分析结果，提出了一个可行的激波不稳定性修正模型，要求在激波区域湍动能产生项的计算式为

式中：b′1为激波非稳态参数，表征由激波不稳定性和上游速度波动之间的耦合引起的阻尼效应，当M1n＜1 时，不应用激波不稳定性修正；u1为激波前的来流速度；c1为激波前的当地声速。M1n是在相对于激波静止的参考系中的测量值。

为将这一约定与原来的湍动能产生项公式耦合起来，故将湍动能产生项中的涡黏性μt替换为，故有

以此实现在激波区域内对k的捕捉［105］。

在k-ω模型中，fs和ξ的求解方式为

式中：激波区域根据比值Sii/Ss确定，在高可压缩区域fs=1，在不可压缩区域中fs=0。

激波不稳定性修正仅适用于k方程。激波不稳定模型改变了平均动能和湍流动能之间的传递，但不影响总能量的整体守恒。此外，使用激波不稳定修正获得的解是稳态的，并且修正考虑的是冲击不稳定的平均效应。采用这一修正可以准确预测激波/均匀湍流相互作用下湍动能k的放大。

后续工作中对C′μ和fs的求解方式为［106-108］

式中：U∞为自由流速度；δ0为入射边界层厚度。Raje 和Sinha［109-110］进一步将激波/湍流边界层相互干扰的物理纳入SST 模型中，此外还纳入了各向异性和流场结构变化的物理模型，类比Menter［2］的分析，湍动能产生项的等效形式为

即湍动能的产生项用等效雷诺应力τeq和平均膨胀Sii表示。根据近壁面边界层附近雷诺应力正比于湍动能的关系，可得

式中：su为考虑激波不稳定效应的参数。

通过变换可以得到

将其写成SST 模型中涡黏系数的表达形式：

需要指出的是，这里使用的是应变率张量的值S，而不是涡量张量的值Ω。对于弱激波，激波非定常模型参数su假定值为2 左右；对于M1n→∞，su的渐近线为1.29，这表明激波不稳定性修正后的结构参数取值在0.4 ≤≤0.62 范围内。更大的产生较小的分离和相互作用区域。 此外激波强度也有影响。 Raje 和Sinha［109-110］选择=0.4 作为激波区域结构参数的极限值，以满足整个马赫数范围的约束，而且选取恒定的结构参数常数值使得模型方便实现。

最后通过对标准SST 模型中混合函数F2进行改进纳入修正，改进后的混合函数为

混合函数F′2保证了只在边界层中有效，然后通过比较，由fs识别出激波区域，它从激波区域外的0 值光滑地过渡到激波区域内的数值1。用到的一些其他关系为

式中：相关变量含义请参考文献［109］。

图4［110］展示了纳入激波/湍流边界层相互干扰现象的SST 模型与其他模型在压缩拐角中的预测结果。通过对比可知，考虑了激波不稳定影响的SST 模型显示出了更好的预测能力，明显改善了对激波诱导分离点和再附着点的预测。

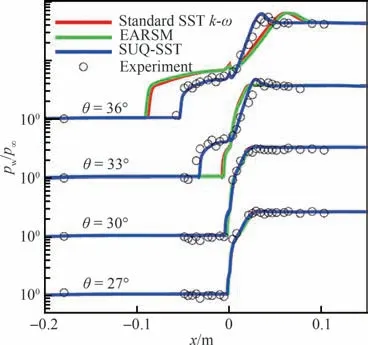
图4 Ma=8 的SWTBLI 案例中不同斜坡角下不同湍流模型与实验数据的壁面压力结果比较［110］Fig. 4 Comparison of wall pressure profile from different turbulence models with experimental data under different slope angles in SWTBLI case of Ma=8［110］

激波区域内各种流动参数变化较剧烈，相应的梯度也较大，该区域内的流动是一个高度非平衡的流动，从广义上说，结构可压缩性和激波不稳定性均表征了高马赫数湍流的非平衡特性，两者之间存在统一，韩省思等［111］指出，开展激波不稳定性修正工作可以在一定程度上借鉴结构可压缩修正的方法和思路。Niu 和Hou［82］也提出根据激波不稳定性会导致湍动能预测过大的现象，可直接在湍动能产生项上设置限定值来实现对激波不稳定性的修正。

上述对激波与湍流边界层相互干扰对流场的影响进行了分析，并给出了一些提高预测精度的方案，然这些方法的主题都是针对流动经过激波区域后湍动能会增加这一现象来开展工作的，有的是直接限定湍动能的产生项，有的是将激波效应耦合在涡黏性表达式上，还有的是通过改进涡黏系数中的常数值来考虑激波/湍流边界层的相互作用效应。然而，目前处理激波问题有效的手段是改进SST 湍流模型中结构参数的数值大小，将激波与湍流边界层相互干扰的物理现象纳入湍流模型中仍需进一步的研究。

2. 4 雷诺应力各向异性效应

在平均应变率突变的、流过曲面的、带二次运动管道的、三维的和激波/湍流相互作用的流动中SST 湍流模型不能获得较好的预测结果［112-113］。在这些流动中，雷诺应力均表现出强烈的各向异性，而SST 模型采用的是雷诺应力与平均应变率之间的线性关系，这使得SST 模型在本质上不能正确地反映这类流场现象。Pope［114］对Boussinesq 线性涡黏假设在具有各向异性的或强逆压梯度的流场中的预测能力不足，提出了非线性涡黏性湍流模型理论，以使雷诺应力表达式具有表达各向异性的能力。非线性涡黏湍流模型基本思想是将一阶应力-应变关系拓展到更高阶，使雷诺应力张量不仅包含剪切应变张量的线性相关项，而且还包含剪切应变张量和旋转应变张量的高阶点积复杂相关项［115］，非线性雷诺应力可以表示为

式中：α′n为模型常数；为流场量的张量形式。

数学上严格推导出的各非线性项表达形式确定不变，但各项的系数不确定，由此可以构造不同的非线性湍流模型。对于SST 湍流模型，2 个输运量仍通过求解常规的两方程得到。

在工程实际应用中，常使用介于一般的线性双方程模型和完全非线性模型之间的中间模型，这在一定程度上能实现各向异性的能力，也能较线性模型更好地预测一些流动现象，并且简单、易于实现，计算量不大。其基本思想是在不引入更高阶应力-应变关系的前提下，改进雷诺应力或涡黏性的表达式［116］。

例如，目前常用的雷诺应力关系：τij=，在i、j、k这3 个主流方向上，正应力引入了湍动能k的影响，但切应力仍采用与应变率的线性关系。又例如，SST 湍流模型使用的涡黏性系数的定义：νt=，在湍流边界层中，采用了Bradshaw 提出的雷诺应力正比于湍动能的假设，涡黏性与涡量有关。

这些方法在本质上偏离了线性的应力-应变线性关系，在某些方向上、某些流场区域中表现出一定的非线性，从而表现了一定的各向异性，但不具有非线性涡黏的通用表达形式，故而称其是弱非线性的。

为了更好地捕捉大流向梯度、流体分离、撞击、流线弯曲/旋转下的流动现象，Wilcox 和Rubesin［117］发展了二阶应力-应变关系的WR 模型。Shih 等［118］也提出了典型的二阶SZL 模型。除此之外，也发展出了一些三阶应力-应变关系的模型：CLS 模型［119］和AL 模型［120］。但这些非线性模型较为复杂，应用不方便，没有得到广泛使用。

事实上，在翼身接合区角回流区流动和三维强激波诱导分离等典型航空分离流流动问题中雷诺应力模型较涡黏模型更有优势［121］。然而，只要将线性的雷诺应力表达式拓展到应力-应变的二阶关系式就能使雷诺应力具有各向异性，能更好地反映流场现象，满足工程应用的需求。RSM输运方程是雷诺应力的具体表达形式，完整地体现了雷诺应力的各向异性，是非线性涡黏模型建模工作很好的起点。基于RSM 发展起来的EARSM 不仅简化了对雷诺应力各项的建模工作，而且为改进涡黏模型本构关系提供了适合的思路和方法。通过将雷诺应力输运模型层面对部分高阶物理过程的描述转移到SST 湍流模型层面上，可解决SST 模型对各向异性预测能力不足的问题，达到拓宽SST 应用范围和预测精度的目的。

Raje 和Sinha［109-110］在扩展标准SST 模型的适用性和有效性范围的工作中，选择了EARSM作为改进非线性关系的研究对象。根据Wallin和Johansson［122］指出的，雷诺应力与平均应变率和涡度张量之间的一般关系可以用有效湍流涡黏性和额外的各向异性项表示：

选择在预测跨声速分离流中取得成功的二次应力-应变关系［123］模化额外的各向异性项，其为局部平均应变率的函数：

式中：τ=1/(Cμω)为湍流时间尺度。各向异性参数的定义为

需要用到的一些其他关系为

式中：gc为Rung 等［123］采用的压力膨胀模型形式的压缩系数修正，模拟了压力-应变关系的膨胀部分，这代表了湍流的重新分布和松弛的机制。

然后通过以下涡黏性关系，耦合到SST 模型中：

式中：F2′ 已在2.3 节中阐述；为实现结构可压缩修正和激波不稳定修正而给出的相关修正函数［109-110］。图5［110］给出了激波/湍流边界层相互作用区域附近值的分布，可以看出改进后的SST模型（SUQ-SST）给出的计算结果与实验得到的流场结构是一致的，在激波/湍流边界层相互干扰的、具有雷诺应力各向异性的流动中给出了较好的预测，即纳入应力-应变二次关系式增强了SST 模型在反映各向异性上的能力。

图5 激波/湍流边界层相互作用区域附近流场实验数据与SUQ-SST 模拟结果对比［110］Fig. 5 Comparison of experimental data and SUQSST simulation results of flow field near shock/turbulent boundary layer interaction region［110］

为了改善Boussinesq 假设的局限性，研究者一直探究实现雷诺应力原本能力的方法，但多年来对Boussinesq 的使用，奠定了涡黏假设关系框架不变是改进研究的基础。目前大多改善雷诺应力表达式的方法是通过增加额外的项或修正模型系数来完善雷诺应力表达式的表达能力，主要是采用流场中的应变率张量和涡量参数。这在一定程度上实现了雷诺应力的各向异性，而且需要较少的计算量，同时也没有增加SST 湍流模型的复杂度。更好地复现雷诺应力的特征，EARSM 和RSM 是雷诺应力进一步改善的主要参考依据。

2. 5 应力-应变偏差效应

目前对k-ωSST 湍流模型已经做了许多改进工作，以解决其在旋转/曲率、可压缩性和各向异性流动中预测不准的问题。然而，这些解决方案在工业中并不普遍使用，因为它们经常被发现要么不可靠（在特定地区改善结果，在其他地区恶化结果），要么不够稳健（难以实现完全融合），要么不完整。每个修复都会带来一系列的问题。从RANS 的角度来看，Boussinesq 假设只使用了雷诺应力与应变率张量的一阶线性关系，即使在非线性等修正中，试图引入二阶、三阶、甚至更高阶的关系，但总的来说，在应力-应变之间仍然存在偏差，而忽略偏差可能会导致过高估计湍流动能的产生，特别是在非平衡湍流中应力-应变偏差起着重要作用。

为衡量Boussinesq 近似关系引起的应力-应变偏差的影响，Revell 等［124］在传统的线性涡黏模型上，研究了应变张量与应力张量主分量之间的不对齐，并称其为滞后模型研究，而所谓的滞后模型是从RSM 模型一个潜在的解导出的，这避免了使用完整RSM 模型的复杂性，同时引入了应力-应变偏差的影响。从本质上说，在应力-应变偏差较大的区域，滞后会改变湍流动能的产生，从而改善湍流剪应力的预测。

一个偏差参数被定义为

通过以下输运方程求解Cas：

将应力-应变偏差的影响引入到SST 公式中，使用Cas来降低发生错位时的湍动能的产量，对涡黏性系数的修正为

式中：Cas的最大限制值为0.3，并使用max 函数确保了涡黏性系数仍然是正的，避免了可能导致的数值不稳定。

Cas输运方程旨在提供与使用全雷诺应力输运模型类似的对平均流动不稳定性的敏感性的描述，同时只求解3 个输运方程，而不是7 个。新增的输运方程改变了耦合SST 两方程的行为，使它得到的结果与RSM 的结果接近。考虑了应力-应变偏差影响的SST 模型比标准SST 模型更能改善平均流场的预测，其预测结果与更复杂的RSM 和成本更高的DES-SST（Detached-Eddy Simulations SST）模型相似。

Lardeau 和Billard［125］扩展了Revell 等［124］的研究结果，建立了修正的椭圆混合滞后输运方程，椭圆滞后的输运参数定义为φ，以衡量应力-应变偏差对涡黏性的影响：

采用椭圆混合雷诺应力模型［126］推导φ的输运方程：

式中：相关变量的含义可参考文献［126］。

滞后方程允许φ(x)捕捉与压力-速度相关性相关的效应，从而增强了预测能力。

模型的椭圆度由α公式建立，其满足

Biswas 等［127］在其基础上发展了“椭圆混合滞后k-ω模型”。尽管滞后模型的动机是表示应力和应变速率之间的不平衡，但它的一个非常重要的方面是对近壁面湍流行为的改进，对中度分离流的预测也有较好的精度。这里使用的椭圆滞后输运参数为φ*，其表达式为

Shang 和Agarwal［128］总结了以上研究者的工作，借鉴其方法将椭圆混合滞后方程引入到SST湍流模型中，提出了椭圆混合滞后SST 模型。k-ω模型与SST 模型有很相似的情况，对Biswas等［127］提出的滞后方法做微调就可以用于求解滞后参数φ*，应用于SST 模型的滞后参数φ*的输运方程为

一些其他项的关系为

引入应力-应变偏差效应的涡黏性系数为

其他相关变量的含义参考文献［128］。

图6［128］给出了驼峰表面压力系数分布预测的结果对比，可知椭圆滞后SST（LAGSST）模型整体性能优于SST 模型，并与实验取得很好的一致性。

图6 二维驼峰上LAGSST 和SST 模型计算的压力系数与实验数据的比较［128］Fig. 6 Comparison of calculated pressure coefficient with LAGSST and SST models with experimental data for two-dimensional hump［128］

随后，Shang 和Agarwal［129］在无壁距（WDF）SST 模型［130］的基础上发展了无壁距椭圆滞后方法。

无壁距椭圆滞后SST 模型的实现主要在于对混合函数F1和F2进行修改：

式中：相关参数的含义可参考文献［129］。

通过几个标准的基准测试用例表明，椭圆滞后方法很好地修正了湍动能的产生，使用无壁距湍流模型的预测精度进一步提高。椭圆滞后混合SST 模型弥补了Boussinesq 近似涡黏性关系的局限性，抑制了湍动能过高的预测，但由于椭圆滞后输运方程的加入，计算时间也相对增加，在未来的发展中寻找更简化的滞后模型将是一个发展方向。虽然该方法通过滞后参数的定义推导而来，但其通过椭圆混合滞后方程纳入了壁面紧邻性。

标准SST 湍流模型采用的是一阶应力-应变关系的涡黏关系式，其截断了二阶项、更高阶项的影响，这在应变率张量值不大的区域是合理的近似，但对于流场梯度变化显著的区域，截断项的影响是不可忽略的。将雷诺应力扩展到二阶项可以实现对旋转/曲率的捕捉，这也在一定程度上表明二阶项、更高阶项的影响是预测不准的原因之一。虽然应力-应变率关系式在本质上存在偏差的影响，但椭圆滞后混合方法可以评估一定的截断影响，而且修正后的椭圆滞后混合SST湍流模型在本质上更趋于完备。

2. 6 层流/湍流转捩效应

除了改善SST 模型在湍流状态中的预测精度外，另一个研究内容是层流-湍流转捩过程对流场细节和整体性能的影响，然而转捩过程可以由许多路径触发，如自然［131］、旁路［132］、分离诱导［133］等，这使得基于物理的方程框架很难对所有这些机制（或其中几个）进行建模。还有就是传统的雷诺平均程序消除了线性扰动增长的影响，然而在转捩流中线性和非线性效应是相关的。工程上除了采用低雷诺数湍流模型外，还通过底层湍流模型的壁面阻尼函数触发转捩的开始。还有一种方法是使用实验相关性，相关性的关系式通常是将自由流湍流强度与转捩开始时的动量厚度雷诺数相关联。为了避免在基于相关模型中需要用到的非局部信息，Menter 等［134-136］提出了基于局部相关性的过渡建模（Local Correlation-based Transition Modeling， LCTM）的统一概念来处理不同的转捩机制，只使用局部信息来激活间歇方程中的产生项，利用涡度雷诺数将相关关系与间歇方程联系起来。间歇因子用于开启转捩点下游湍动能的产生项。转捩起始动量厚度雷诺数用来捕捉湍流强度的非局部影响，这里湍流强度的变化是由于自由流中的湍流动能的衰减，以及边界层外自由流速度的变化。2 个输运方程已经被建立起来：一个是湍流间歇输运方程γ，另一个是转捩动量厚度雷诺数的输运方程，被称为模型，模型方程为

将间歇公式与SST 湍流模型耦合实现对转捩过程的预测，它是根据转捩动量厚度与应变率雷诺数的关系来打开转捩点下游湍动能的产生项。引入转捩过程的SST 模型为

一些其他关系为

式中：γreff为有效间歇因子。

此外，需重新定义SST 湍流模型中的函数F1使其在层流边界层中也可使用。方法为

式中：F1orig为标准SST 模型中的混合函数F1。

间歇因子γ对湍动能k方程有直接的影响，而过渡动量厚度雷诺数Reθt只对间歇因子有直接的影响。改进后的SST 模型能够更加精确地预测自然、旁路和分离诱导的层流转捩的位置。

后来，Menter 等［134-136］充分披露了γ-Reθ模型完整的相关性，以便继续进一步验证和可能的扩展或改进［137］。孟德虹等［138］指出在中等雷诺数范围，层流区域和湍流区域有相同的量级，采用γ-Reθ模型才能更准确地模拟气动力。

Hou 等［139］在γ-ReθSST 模型的基础上耦合了基于等效沙粒方法［140］的表面粗糙度修正，几种不同模型对转捩过程预测的对比如图7［139］所示。考虑粗糙度的修正模型也能很好地呈现层流-湍流转捩过程的相应趋势。γ-Reθ模型在和EARSM 模型结合的模拟中也取得了更好的结果，肯定了通过间歇性因子实现对转捩过程捕捉研究的可行性［141］。

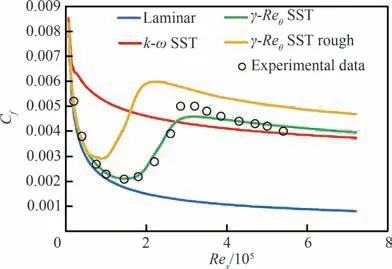
图7 有粗糙度的T3A 平板表面摩擦阻力分布［139］Fig. 7 Surface frictional resistance distribution of T3A plate with roughness［139］

Barrouillet 等［142］也对这一模型进行了修改和重新校准，以更好地匹配实验结果。一些改进如下：

1） 提高对沿表面的过渡起始点的预测，又不影响其他特征，改进了Fonset3，得到

2） 为了避免在一些情况下，在前缘位置处有非物理解，将FTu的计算式修改为

3） 采用的湍动能方程中耗散项的计算式为

4） 研究发现，不可微函数会引入不稳定性，阻碍收敛。Piotrowski 和Zingg［143］提出了相同的观察结果，故对Fonset公式作出改进：

式中：相关变量可参考文献［142］。

根据Durbin［144］和Ge 等［145］基于局部变量单个间歇输运方程提出的转捩模型，Menter 等［146］对γ-Reθ模型进行了改进，给出了只用间歇因子的输运方程与SST 模型结合的模型。改进后的间歇因子输运方程为

式中：Pγ为转捩源项；Eγ为耗散项/再层流化源项。

这里间歇因子γ触发层流边界层向湍流边界层的转变。在自由流中，间歇因子被设置为1，在层流边界层中，间歇因子向0 变小。

耦合了转捩过程的SST 湍流模型为

需要指出的是，为了避免滞止区湍流强度过高，对湍动能产生项采用Pk=μtSΩ［147］计算（注意，当使用此公式时，标准SST 模型中产生项的限制器停用）。相比γ-Reθ模型，这里在k方程中还引入了一个额外的产生项，以确保在任意低（降至0）湍流强度水平下，在过渡点产生适当的k。该方法能很好地预测转捩现象，包括起始位置和转捩长度［148］。

一般工业CFD 基本上不考虑转捩过程的影响，这不仅在于转捩方式种类多，而且在平均流场中也难以实现对转捩过程的捕捉。然而提出的LCTM 概念较好地解决了这些问题，并发展出了转捩模型，而且对于基础湍流模型而言，转捩模型的间歇性概念是通用的，容易与SST 湍流模型相结合，其只需要通过间歇性因子控制湍动能方程中的产生项和耗散项，从而将转捩过程对湍流发展的影响纳入模型中。

2. 7 基于数据驱动技术的模型改进研究

基于理论模型框架建模虽然降低了湍流计算复杂性，但不可避免地引入了不确定性和误差，而且需要研究者对物理过程有深刻的理解。近年来，Weatheritt 和Sandberg［149］指出，通过对高保真仿真/实验数据进行机器学习可以促进对不确定性的理解并减小误差。对此，学者们已开展了许多基于数据驱动技术对湍流模型改善以及更复杂机器学习方法应用的研究工作［150］。

鉴于Boussinesq 线性涡黏本构关系是导致湍流模型在非平衡、分离和激波/湍流边界层干扰等流动中预测不确定性和误差的主要来源［151］，Ling 等［152］指出预测的雷诺应力差异是基于数据驱动技术研究的合适目标，而且现有的非线性涡黏模型［114，119，122］因其可以在理论上弥补线性涡黏模型的缺陷，还可以通过平均流场的物理量来定量解释高阶非线性涡黏关系式与线性涡黏关系式之间的差异，是用于机器学习很好的先验假设。Wang 等［153］进一步指出，这些差异可能是普遍的量，并且可以从一种流动外推到另一种流动，至少在具有相同特征的不同流动之间是这样的，例如分离流。

Weatheritt 和Sandberg［149］选取BSL 模型作为机器学习的基准模型，根据经典EARSM 模型的雷诺应力本构关系，选择以下4 个基函数和2 个标量不变量来构造非线性涡黏假设的各向异性部分：

采用M-GEP（Multidimensional Gene Expression Programming）算法在BFS（Backward Facing Step）和PH（Periodic Hills）流动算例中进行机器学习和训练，分别得到了以下2 个函数：

式中：τI为湍流时间尺度。2 个函数都来自算法的2 次单独运行，这意味着不同的初始种群和随机常数产生了2 个语法相似的函数，同时也表明非确定性算法已经收敛到结构组成相似的表达式，这是令人兴奋和鼓舞的。

图8［149］显示了基于机器学习方法改进的BSL 湍流模型在PH 算例下x/h=4.0 处的应力和速度曲线图，其中M-GEP 样本的置信区间的均值为99.9%，表面摩擦力系数和速度分布与实验结果吻合，预测的雷诺应力也在趋势上取得了更好的一致性，在一定程度上表明了基于机器学习方法研究湍流模型改进的可能性。米俊亦［154］对雷诺应力展开了研究，结果也表明数据驱动技术有助于重新构建雷诺应力的本构关系。孙亮［155］也探究了机器学习算法对湍流模型预测能力的改善。

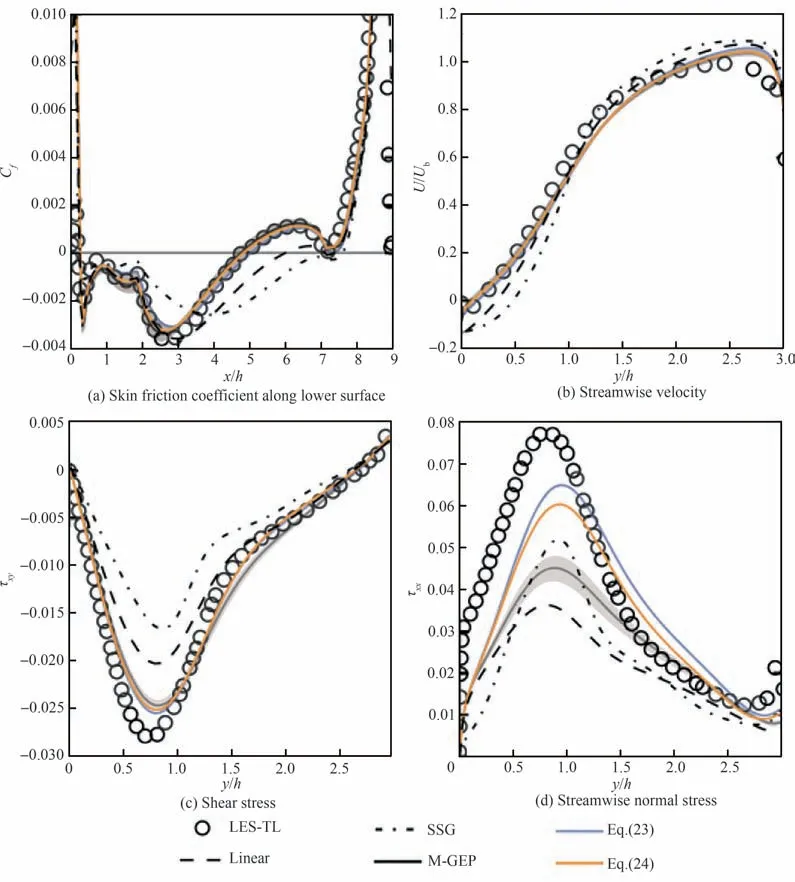
图8 PH 算例的统计结果［149］Fig. 8 Statistical results from PH Case［149］

近期，Banko 和Eaton［156］提出最佳张量基扩展的概念，通过最优扩展实现给定张量基与流场各点的真实各向异性张量的最佳拟合。叶舒然等［157］也指出卷积神经网络强大的非线性映射能力以及分层提取信息特征的功能是当下流场特征研究不容忽视的工具。基于数据驱动发展流体力学多学科、多物理耦合建模以及流动智能自适应控制等方面是有益的［158］。

目前数据驱动技术主要是使用神经网络、基因表达编程或随机森林的机器学习方法在与要预测的流动具有相似特征的训练流DNS（Direct Numerical Simulation）数据库/高保真LES 数据库中来学习和训练，构建局部平均流场标量和张量与建模项之间的复杂函数［159-161］，其中建模项的主要对象是雷诺应力的各向异性部分和单方程的涡黏性。一些经此修正的湍流模型已在曲面壁流、方形管道二次流以及不对称扩散器分离流中进行测试，计算精度得到一定改善。

虽然基于数据驱动技术改进湍流模型的研究取得了一定的成功，但是该方法也产生了新的问题，即用于数据驱动技术开展训练的流场是特定的或是特定的参数范围，由此得到的修正模型在推广到更广泛的流场或更通用的条件中仍需进一步工作。结合机器学习开展湍流模型改进研究大多是对k-ε、k-ω和S-A 湍流模型开展的，针对SST 湍流模型的研究少有报道。而SST 湍流模型在边界层中使用了雷诺应力正比于湍动能的假设可能会是制约该研究工作的一个挑战。此外，尽管基于机器学习的模型改进工作已经取得了一定的成功，但基于机器学习的改进是否受到选取张量基、输入特征或算法等因素的限制尚不清楚。

3 结论与展望

SST 湍流模型面世以来，得到广泛研究和应用，是目前使用最广泛的模型，在很多问题上取得很好的预测效果，但是还存在预测精度不高、应用范围局限以及改进模型难以拓展等问题，主要原因是：① Boussinesq 线性涡黏关系式；② 忽略了一些力或高阶脉动关联项的影响。

针对此，学者们开展了旋转/曲率、可压缩性、激波不稳定性、雷诺应力和层流/湍流转捩等方面的改进，并取得了较好的研究成果。从基于局部信息来主动控制宏观湍流量表达转变为通过力的作用来影响湍流量的表达，能够使SST 模型得到更好的改善。对现有的研究成果和研究内容进行整理，可以发现集成/耦合出更加完备的湍流模型是一个有前景的研究方向，目前耦合雷诺应力模型与SST 模型的工作以及合并雷诺应力各向异性、激波不稳定性和可压缩性结构变化的工作证明了该方法的可行性。

然而，目前开展的这些工作还没有完全解决问题。构造流场中剪切应变率张量、涡量、湍动能、当地声速等物理量的函数关系式，然后将该函数结合到湍流模型方程中的某些项或模型常数上，从而改变这些项或常数的表达，实现对预测结果的修正，但是这种修正会因流场结构的不同而表现出不一样的预测能力，存在预测性能的不确定性。针对这些物理量，采用不同的分析方法和组合方式可以得到解决不同物理问题的修正函数，但这些函数有可能是作用于同一项或同一模型常数，所以也很难判断耦合多种修正策略的方法是改善预测还是破坏预测。

此外，现有的改进工作大多是对基于不可压缩条件开发的SST 湍流模型开展的，对基于可压缩条件下SST 的发展和改进仍然较少。学者们已经对膨胀耗散、压力膨胀耗散和压力做功展开了可压缩效应研究，但大多是构建梯度马赫数或湍流马赫数与不可压缩湍流模型中的产生项、耗散项等的函数关系式进行修正，而这种可压缩效应修正策略与湍流模型纳入其他物理现象的修正在实现方法上是基本一致的，最终均是改变某些项的系数的表达来纳入相关效应的影响，所以可能由于相同的原因导致耦合可压缩修正工作进展缓慢。

近年来基于数据驱动技术研究湍流模型为改善仿真计算提供了另外一种研究策略。基于数据驱动技术改进湍流模型能够一定程度上提高复杂流场的预测准确性和时效性，并降低模型封闭或湍流相关变量建模的难度，这是有吸引力的，但是也面临着亟需解决的新问题。目前的工作主要在于改进雷诺应力各向异性部分和涡黏性，然而改进是否会受到算法、输入特征量等因素的影响还不清楚。选取SST 作为基准模型的机器学习研究也少见报道。

通过对SST 湍流模型改进研究的不断深入探索和学习，对于进一步发展SST 湍流模型，有以下几点值得注意：

1） 合理集成现有物理现象的研究成果仍是SST 湍流模型改进研究的可行方案之一。

2） 对耦合不同的修正方案存在预测性能不稳定以及实现自适应的问题，需进一步研究揭示耦合的内在机理。

3） 纳入可压缩效应修正的耦合研究有待加强。

4） 基于数据驱动技术开展SST 湍流模型改进研究是一个颇有前景的方向。