航天高性能薄壁构件的材料-结构一体化设计综述

张卫红，周涵，李韶英，朱继宏，周璐

西北工业大学 航宇材料结构一体化设计与增材制造装备技术国际联合研究中心，西安 710072

航天重大装备是国际竞争的战略制高点，是国家整体制造实力的重要体现。复杂薄壁构件是航天装备最重要的主承载结构，如高超声速飞行器舱体、运载火箭箭体、航天发动机尾喷管等。这类复杂薄壁构件多服役于严酷的热机械耦合环境。以高超声速飞行器舱体为例，需满足飞行气动加热、再入大气层、高机动过载、超远程巡航等服役条件，要求具备超强承载、极端耐热、超高精度、超轻量化等特性。这些要求对传统结构设计方法提出了严峻挑战，特别是防热与承载独立、材料与结构分离的设计模式已无法充分挖掘材料和结构在不同尺度下的性能潜力，结构减重和性能提升面临技术瓶颈。因此，发展先进材料-结构一体化设计方法理论、突破多材料多尺度结构的整体制造技术瓶颈、准确描述和精确调控材料与结构的交互作用成为突破传统设计性能极限、实现高性能构件制造的关键。

近年来，国外高超声速飞行器、先进航天运载器飞行故障分析表明，航天薄壁构件热结构失效问题、结构维形失效问题、振动失效问题的根本原因均可以归结于严酷热-机械耦合载荷环境下构件材料-结构-性能的不匹配设计。为了保证严酷服役环境下的结构防热、承载、振动等综合性能以及轻量化设计要求，必须从多个尺度以及设计制造多个层面更深入地挖掘材料-结构潜力，提升材料、结构、工艺等多种因素匹配设计水平。

1 相关研究内容

1. 1 材料-结构的多尺度建模与性能表征

结构件性能取决于材料-结构宏微观构型和不同制造工艺条件形成的组分性质，精确描述二者之间的映射关系是深刻认识材料-结构宏微多尺度建模和性能表征原理的基础，也是实现材料-结构多尺度一体化设计的前提。多年来，国内外学者发展了多种解析、半解析和数值多尺度分析方法，如均匀化方法［1-3］、Voronoi 单胞有限元法［4-6］、多尺度有限元法［7-10］、局部拉格朗日乘子方法［11-12］、代表单胞分析方法［13-14］、镶嵌单胞方法［15-16］，构成了材料-结构多尺度分析的理论基础。

20 世纪70 年代，均匀化理论将周期性的非均质结构等效为宏观均质材料［1］，形成了双尺度渐近分析方法。在宏微观两个尺度下，由微结构单胞计算出宏观尺度下材料的等效物性参数，从宏观平均场方程出发利用双尺度渐近展开计算出微观尺度下物理量的局部涨落，实现材料-结构位移场、应变场和应力场局部表征［17-18］。梁军等［19］利用双尺度方法模拟了三维编织复合材料的力学性能。Zhai 等［20］应用均匀化方法实现了三维编织复合材料的热-机械性能双尺度模拟。均匀化方法可有效减少多尺度计算量，但是无法反映宏微观结构之间的真实尺度比例。

Feyel 和Chaboche［7］针对非线性结构发展了基于均匀化理论的多尺度计算均匀化方法，通过有限元方法嵌套求解宏微观两个尺度的边界值问题，也被称作有限元平方法或多尺度有限元法。该方法仅需定义微观尺度各组分材料的本构模型，宏观尺度的材料本构则由其所对应微结构单胞的等效应力-应变关系直接决定，充分考虑了微结构复杂几何特征和本构模型对宏观机械力学响应的影响，目前已成为多尺度计算领域应用最广泛的计算模型。与此同时，多尺度有限元法存在两大制约因素：①空前的计算消耗和存储需求，尤其是涉及与加载路径相关的复杂非线性材料本构模型，因此相关学术研究也基本局限于二维问题；②实际工程结构的宏微观尺度的比例常不符合均匀化理论尺度分离的模型假设，难以通过该模型精确有效地表征结构的力学性能。

近年来，基于快速傅里叶变换（Fast Fourier Transform， FFT）的均匀化算法被广泛应用于诸如纤维复合材料的强非均质介质的等效宏观性能表征相关研究［21-24］。Vondřejc 等［25］提出了应用FFT 均匀化算法的Galerkin 有限元方法，并计算了宏观等效性能的上下限。值得注意的是，基于FFT 的均匀化算法仅在求解网格规则划分的非均质介质例如高精度电镜材料微结构图片时，相对其他均匀化算法才具有显著的计算效率优势，同时在处理非线性问题时该方法仍具有相当的局限性。

另一类尺度关联的计算策略是区域分解，直接将宏观结构离散成多个子结构，通过约束子结构界面间的位移或应力一致来实现整体结构和离散子结构的耦合迭代求解。Ladevèze 等［26］发展了一种求解此类问题的混合法，无需满足子结构界面间位移/力的一致性，同时结合该团队开发的迭代求解算法，可有效实现宏观结构和子结构的耦合迭代求解。Ibrahimbegović 和Markovič［27］采用类似的区域分解计算策略实现了非弹性非均质结构的多尺度模拟。然而，该策略仅适用于宏微观尺度接近的情况，当微观尺度几十甚至上百倍小于宏观尺度时，将导致巨大的计算量以及非线性求解难以收敛的问题。

1. 2 材料与结构优化设计

材料-结构多尺度建模与性能表征是实现材料-结构一体化设计的基础，而以拓扑优化为核心的多尺度结构设计方法是实现航天薄壁构件材料-结构一体化的关键手段。

拓扑优化最早可以追溯到Cheng 和Olhoff［28］提出的薄壳厚度拓扑分布优化以及Bendsøe 和Kikuchi［29］提出的基于均匀化的连续结构拓扑优化设计方法。这期间，形成了以密度变量法（Density Based Method， DBM）［30-31］、渐进结构优化方法（Evolutionary Structural Optimization，ESO）［32-33］、水平集方法（Level Set Method，LSM）［34-35］等技术为代表的不同设计方法，并在机械工程、航空航天结构设计领域得到广泛应用［36］。然而，单纯考虑宏观构型设计的拓扑优化方法仍然没有充分发挥材料的承载和多功能潜力。为此，在航空航天和高端机械装备应用需求的推动下，国内外众多院校与科研机构开始从细观力学、材料-结构多尺度计算等方面积极探索材料与结构宏微观匹配的优化设计新理论与新方法。

20 世纪末，Lakes［37］提出了具有负泊松比的泡沫多孔材料构型并发现不同组分材料的复合可以获得单相材料无法实现的极端特性，如零热膨胀系数。在此启发下，Sigmund［38］提出了基于均匀化理论与拓扑优化方法的各向同性材料单胞构型逆向设计技术，根据预先给定的性能要求进行微结构构型设计。这一思路使材料微结构拓扑优化设计可以同时从材料与结构多个尺度入手，获得了进一步减轻结构重量、改善材料与结构性能的机会。从此，微结构设计、等效性能计算以及微结构对宏观性能的影响规律等基础问题引起了世界上众多学者的关注，并发展了以材料特定性能为目标、基于均匀化方法的微结构逆向设计与正向设计等技术［39-40］。刘书田和程耿东［41］开展了基于均匀化理论的梯度功能材料优化设计研究。袁振和吴长春［42］研究了具有最大等效弹性模量或刚度的周期性微结构以及复合材料扭转轴截面的微结构拓扑优化设计技术。近期，Huang 等［43］采用双向渐进优化方法实现了材料微结构的刚度最大化设计、电磁性能优化设计以及粘弹性性能优化设计。Xia 和Breitkopf［44］详细阐述了基于能量法的均匀化分析以及材料微结构拓扑优化设计的流程。Cadman 等［45］综述了材料微结构拓扑优化的相关研究进展。

随着拓扑优化方法在材料微结构领域应用的日渐成熟，更多的研究关注投向了多尺度材料-结构一体化设计。Rodrigues 等［46］在假设宏观结构由单一材料微结构、多种微结构组成及组分材料用量一定的条件下，实现了保证宏观结构刚度最大的微结构优化设计。Adams 等［47］指出微结构设计与宏观结构设计具有不可割裂的相互内在联系，阐述了材料-结构一体化设计的内涵。Zhang 和Sun［48］采用微元单胞超单元建模、宏微串行设计的思路发展了关联尺度效应的宏微结构多尺度优化设计方法。Yan 等［49］采用基于均匀化的宏微观协同优化方法开展了热弹性结构的拓扑优化设计，并开展了热力耦合作用下的刚度和传热多目标双尺度结构拓扑优化设计。Su 和Liu［50］假定宏观结构由具有一定孔隙率的均一微结构构成，通过拓扑优化实现了宏微观结构构型协同设计。Xia 和Breitkopf［51］提出逐点开展微结构设计，即假定宏观结构的每一个材料点对应一个独立的微结构设计，同时通过非线性求解策略实现宏微观尺度的机械性能耦合计算并建立代理计算模型，替代微观尺度材料优化设计，实现双尺度结构拓扑优化设计，并综述了多尺度拓扑优化设计相关研究进展［52］。

拓扑优化也在复合材料领域得到了广泛应用，设计纤维取向、铺层厚度、空间材料分布等，提高超轻复材构件的力学性能［53］，需要将复材结构设计域离散为一系列空间密度，通过梯度算法得到具体取值［54］。而对于纤维取向等工艺参数变量的处理，经典方法是将纤维取向和单元的第一主应力的方向耦合起来，建立多尺度/多相材料的拓扑优化数学模型进行求解［55］。Boddeti等［56］建立了多尺度的复材板壳拓扑优化流程，协同设计了结构构型和短切纤维的取向。在此工作基础上，Boddeti 等［57］进一步提出了基于多材料喷射增材制造技术的变刚度复合材料设计方法，通过几何视觉处理方法将短切纤维连接为长纤维。Papapetrou 等［58］集成了密度法和水平集方法的优势，对宏观结构构型和纤维取向排布进行了协同设计，证明复合材料拓扑优化可通过多种数学方法实现。

1. 3 结构增材制造

高性能复杂薄壁构件的设计方案最终要依赖先进的制造手段来实施。传统制造工艺多局限于均质材料和单一尺度结构，几乎无法满足高性能航天薄壁构件材料梯度分布和多尺度结构的整体制造要求。增材制造技术的快速发展为复杂结构的制造提供了新的途径。增材制造通过材料逐层叠加的方式可以实现复杂构件的快速制备，有效避免了铸造、锻造工艺中脱模方向限制和切削工艺中的刀具可达性限制等问题。但仍需考虑最小尺寸、悬空角、连通性等工艺约束问题［59-61］。

王华明团队开发出了大型钛合金增材制造装备系统［62］。Huang 和Lin 采用激光熔化沉积技术制造出C919 客机翼肋缘条，长度达3 100 mm［63］。Yang 等［64］从材料、结构、工艺、性能等方面实现了多种仿生结构设计与调控。增材制造技术的快速发展为大型、复杂结构件的整体成形提供了重要途径，然而金属经历的循环熔化冷却历程以及传热的非均匀性非常容易产生组织缺陷，影响成形结构件的性能，而且激光加热产生的热应力也易导致大型结构件的翘曲变形，为激光成形工艺中的控形与控性带来了挑战，顾冬冬等［65］对航空航天结构件的增材制造进行了详细综述。

增材制造技术为多材料或材料梯度分布的复杂构件整体制造提供了新的解决方案，摆脱了传统制造工艺无法实现构件内部材料分布可控的局限性。刘建涛等［66］利用激光立体成形技术制备了Ti-Ti2AlNb 梯度材料，实现了α 型钛合金经α+β 型及β 型钛合金向Ti2AlNb 基合金的梯度转变。随后，杨模聪等［67］利用激光立体成形制备了沿成形方向成分连续变化、外形规整的Ti60-Ti2AlNb 梯度材料。解航等［68］利用激光金属直接成形了Ti6Al4V-CoCrMo 梯度材料实体件，尽管CoCrMo 组分体积分数在10%时形成了均匀的Ti6Al4V-CoCrMo 有限固溶体，但由于两种组分的热物性属性不匹配，当CoCrMo 含量在20%和30%时，在结构内部出现显著的应力集中，形成裂纹源，甚至出现开裂现象。目前相关研究仅能实现材料在特定方向上的梯度分布，如何制造组分任意梯度分布的高性能复杂结构仍面临较大的技术挑战。

本研究结果和其他有关研究结果有些不一致[2]，这可能和本研究样本所在地区有关系,在江西,男女教师的角色职责差异较小,男女教师有着相同的自我发展的社会需求,也同样承受着来自于家庭、职业的压力,因而健康水平相当。但由于男女间不同的身心特点和承担不同社会分工所致：女性在个性方面则相对比较敏感、细腻，承担家庭更多繁杂的琐事。男特级教师更具有自信和果断的性格,若走向极端,便有可能使其变得偏执,更具有敌意。

增材制造过程中由于散热不均导致晶粒组织沿不同方向生长速度不同，如采用选区激光熔融技术制备Ti6Al4V 材料时，晶粒会沿着成形方向以柱状方式生长，导致宏观材料属性表现出显著的各向异性［69］。同时，制件在成形过程中经历了周期性、剧烈、循环加热冷却的复杂热物理过程，导致组织晶粒形态复杂多变。此外，成形过程中产生的未熔融区域、气孔等缺陷，是影响结构件疲劳性能的重要因素。 Edwards 和Ramulu［70］在研究选区激光熔融Ti6Al4V 的疲劳性能时，利用热等静压处理，通过高温高压共同作用改善内部缺陷和晶粒组织的方向性，提升了疲劳性能。此外，在制备多材料结构时由于材料界面的热物性梯度变化剧烈、热应力过大，极易引入制造缺陷，引起热失效。因此多材料梯度、多尺度结构的整体制造技术已成为未来高性能构件制造的关键。

2 研究热点

2. 1 结构设计中的制造工艺约束建模方法

结构可制造性是拓扑优化设计的一个重要研究方向，在结构设计时考虑制造技术中的工艺约束，包括铸造、锻造工艺中的拔模约束，切削工艺中的刀具可达性约束，增材制造中的连通性和悬空角约束，才能实现结构设计和工艺约束的一体化，避免结构无法制造或修改结构破坏性能等问题。

在传统制造工艺中，铸造、锻造中的凹坑、拔模方向，切削加工中的刀具形状、尺寸以及刀具可达性等是考虑较多的因素。在涉及铸造约束的工作中，Sato 等［71］提出了一种虚拟物理模型用于评估铸造结构的可制造性。Wang 和Kang［72］结合水平集法建立了一种区域积分形式的约束。Hou 等［73］在设计加强筋的同时考虑了拔模方向。Li 等［74］使用改进的虚拟温度场模型解决了单向或多向铸造中结构出现凹坑、封闭孔洞的问题。Wang 等［75］额外进行了分型面位置的优化。

考虑切削工艺约束时，Langelaar［76］和Lee等［77］基于密度法分别采用密度过滤、密度投影的方式考虑了刀具形状、长度等因素对优化结果的影响。Gasick 和Qian［78］计算并约束了结构中刀具不可达的材料体积。Mirzendehdel 等［79］识别多轴加工中不可制造的特征并建立了通用的度量方法。Morris 等［80］在水平集方法的基础上通过限制边界移动速度施加制造约束。

增材制造的出现有效扩展了设计空间，但其独特的工艺约束如悬空角、连通性、最小尺寸约束等无法忽略。针对悬空角工艺约束的工作主要涉及自支撑结构的拓扑优化方法研究，即设计满足悬空角条件的结构以达到无支撑制造的目的。在密度法的框架下，Langelaar［81］、Johnson 和Gaynor［82］通过比较上下层单元密度关系逐层过滤密度场获得自支撑结构。Van 等［83-84］利用前传播的时间延迟对密度场进行整体过滤实现自支撑结构设计。Qian［85］、Zhang 等［86-87］利用密度梯度信息构造约束限制结构中的悬空角。Liu 等［88］采用密度过滤技术实现自支撑填充结构设计，同时结合最小尺寸约束可以调整自支撑结构进一步演化为多孔结构，如图1 所示。Wang 等［89］基于参数化B 样条方法建立边界角度约束。在水平集法的框架下，Allaire 等［90］和Wang 等［91］分别建立了边界积分式以及区域积分式约束限制结构悬空角。Guo 等［92］针对可移动变形组件和可移动变形孔洞建立了悬空角约束。Zhang 和Zhou［93］、Zhou 等［94］利用多边形、多面体有限边界的几何特性实现了悬空角控制。

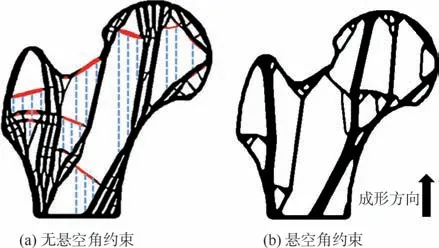
图1 自支撑结构设计［88］Fig. 1 Design of self-supported infilled structures［88］

围绕结构连通性研究，Li 等［95］在空腔中赋予高导热材料、实体赋予隔热材料建立虚拟温度场，通过限制最大温度保证结构连通性。Zhou 和Zhang［96］基于孔洞特征的移动、变形和融合实现结构优化，并通过控制孔洞特征的位置实现连通性约束建模。Xiong 等［97］建立连接封闭孔洞之间的通道或封闭孔洞与结构边界之间的通道来保持结构的连通。Gaynor 和Johnson［98］结合悬空投影和孔洞投影实现无封闭孔洞的结构设计。

围绕结构最小尺寸控制方法研究，Dunning［99］针对参数化隐式方程的拓扑优化建立了通用的最小尺寸约束，可同时实现实体和孔洞的最小尺寸控制。Hoang 和Jang［100］、Wang 等［101］通过直接约束可移动组件的几何设计变量，并且在组件相交处施加约束达到了结构最小尺寸控制的目的。Liu 和Ma［102］通过建立多个水平集场实现了多材料结构的最小尺寸控制。Liu［103］实现了结构最小尺寸的分段控制。

随着先进制造工艺的不断发展，如多轴增材制造系统和增-减材制造系统，可以有效避免一些常见的工艺约束，如悬空角约束，进而显著提升对复杂构型的制造能力。然而复杂的制造工艺也对制造效率和时间成本提出了更高的要求，因此高效的工艺规划建模研究也成为了拓扑优化设计与先进制造技术深度融合的重要发展方向。

2.2 制造工艺参数与结构协同优化设计

当结构设计满足制造约束后，零部件在制造过程中，其微观材料性能，包括延展性、强度和韧性等力学属性，会不可避免地受到工艺参数的影响。例如在铸造过程中，由于冷却速率不均匀，在大型铸件中容易出现枝晶、成分偏析和孔洞裂纹［104］，常通过锻造加工使铸件中的粗大枝晶和柱状晶粒转变为晶粒较细、大小均匀的等轴再结晶组织，提高金属的塑性和力学性能［105］。和常规工艺相比，金属激光增材制造可调整局部熔池的热量，最终形成容易调控的组织结构，已经在复杂航天薄壁构件制造中得到了大规模应用［106］。在典型高温载荷下，Dai 等［107］建立了选区激光熔化成形的铝合金修正Arrhenius 模型，预测了热变形条件下铝合金的流动行为和组织演变规律。Souza 等［108］在Arrhenius 模型的基础上，建立了经验公式下的钛合金高温变形本构模型。

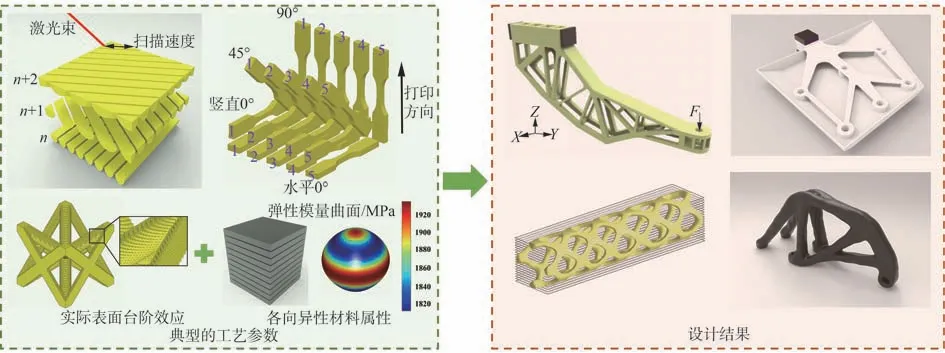
图2 增材制造工艺-结构协同优化［113-114］Fig. 2 Integrated process-structure optimization for additive manufacture［113-114］

除此之外，制造过程往往会引入额外的几何误差。Park 和Rosen［115］对实际打印结构进行了纤维观测和拉伸测试，发现分层造成的表面台阶效应对零部件力学性能具有较大影响。对于精细结构，尤其是微观点阵结构，这种表面几何误差会导致实际点阵力学性能严重偏离初始设计。因此，Li等［116］在点阵设计阶段考虑了增材制造工艺引起的材料各向异性和几何台阶效应，从设计源头上规避制造工艺带来的性能偏差，并且基于统计值给出了点阵结构工艺-尺寸参数通用设计准则。

2. 3 材料结构一体化设计

多尺度结构优化设计同时从宏观和微观充分发掘材料的应用潜力，是发展高性能、轻量化、多功能先进结构的重要途径，受到了国内外学者的广泛关注和研究。早期的多尺度结构优化设计工作由于过度追求设计自由度导致了设计变量多、计算规模巨大、相邻微结构难以保证连接性等问题。如何减小计算量、约束相邻微结构连接性和保证可制造性是近期材料结构一体化设计的重要研究焦点。Wang 等［39］基于同一水平集函数利用形状插值技术构造一系列构型渐变的微结构，这些微结构在边界上呈现出相似的材料分布和拓扑特征，因此自然地保证了相邻微结构之间的连接性。Li 等［40］依据宏观单元密度对微结构进行分类，具有相同密度的单元对应同一种微结构，有效减少了微结构的种类，同时在相邻微结构之间设置刚性连接点保证相邻微结构的连接性。随后，Gao 等［117］通过正则化的变厚度法首先获取宏观单元密度分布，并根据密度值分类得到多片式密度区域分布，每个区域对应一种微结构，其密度值作为后续优化的微结构体积分数约束；然后运用水平集方法和数值均匀化理论实现宏微观协同优化。Zhang 等［118］将形状插值技术构造可连接性微结构的方法应用到多尺度点阵动力学设计，实现了频率响应最小化的优化设计。为改善纯点阵结构的力学性能，Chu 等［119］在宏观尺度上应用参数化水平集方法描述点阵外层涂层的分布，配合密度法优化不同种类点阵结构分布，实现了点阵填充涂层结构的协同优化设计。Wang 和Kang［120］提出了基于密度模型和水平集模型的协同优化框架，在宏观尺度上基于速度水平集方法可以直接获得不同类型微结构的分布，在微观尺度上基于密度方法进行单胞构型设计，同时设置刚性连接点保证微结构的连接性。Xu 等［121］基于特征驱动的拓扑优化方法提出了多尺度协同优化模型，在宏观尺度上每一个宏观特征对应一种微结构，既保证了微结构种类的灵活性选择同时又减少了设计变量数目，显著提高了计算效率。Groen 和Sigmund［122］提出了一种投影方法将基于均匀化的拓扑优化结果映射为高分辨率可制造的结构，使复杂的周期性微结构可以在细观尺度上平滑连续过渡，如图3所示。

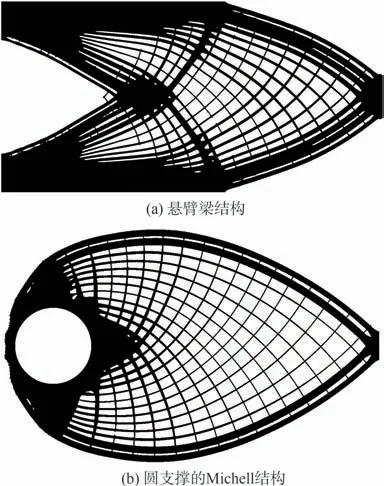
图3 多尺度结构优化设计［122］Fig. 3 Multiscale structure optimization design［122］

然而，在上述研究工作提出的多尺度结构优化模型中，需要重复对微结构进行宏观性能等效。为避免这一弊端，Wang 等［123-124］提出了参数化点阵结构和代理模型的概念，即预先由一组或多组参数控制生成一系列微结构样本库，并基于均匀化理论等效其宏观力学性能，随后采用多项式插值建立微结构宏观性能与控制参数之间的映射关系。这一过程不仅与优化过程互相分离，而且可以重复应用于不同的优化问题中，有效的兼顾了设计自由度和计算效率。对简支梁结构的数值仿真和试验测试均验证了此方法的有效性，如图4 所示［123］。White 等［125］以神经网络作为代理模型，对多参数控制的点阵性能预测比多项式插值表现出更好的拟合能力。

图4 基于参数化点阵的MBB 梁优化设计结果［123］Fig. 4 MBB beam optimization design results via parameterized lattice［123］

基于均匀化理论的多尺度结构优化设计方法依赖尺度分离假设。围绕考虑尺度效应的多尺度优化方法研究，Wu 等［126］基于子结构法提出了近似降阶惩罚模型，建立了密度变量与点阵刚度矩阵之间的关系，通过适当调节惩罚因子达到调控宏观结构的目的。由于将点阵单胞视为一个超单元，因此避免了均匀化理论带来的尺度分离效应。在此基础上，Liu 等［127］结合多材料插值模型实现了混合点阵的匹配设计。Wu 和Li［128］采用多扩展多尺度有限元方法实现了共形点阵结构的尺寸优化，有效提升了计算效率。Zhou等［129］基于参数化点阵和多尺度有限元方法提出了实体-点阵的混合变量优化模型，避免了均匀化理论中的尺度分离假设。Wu 等［130］对多尺度结构优化设计进行了详细的综述。

直接采用梁单元对点阵结构进行全尺寸建模也可以避免尺度分离效应。Chen 等［131］采用预定义点阵单胞替换实体单元的方式实现大规模点阵结构的参数化建模，以杆径为设计变量建立参数优化模型得到梯度点阵结构。Tang 等［132］提出了点阵/蒙皮结构优化设计方法，在点阵区域采用梁单元进行参数化建模，并采用ESO 方法优化点阵尺寸。然而，采用梁单元对点阵建模的同时也引入了额外误差［132］：①梁单元在节点处重叠部分使统计体积偏大；②材料堆积使节点附近实际刚度偏大。

多尺度结构一体化设计在静力学和动力学领域取得了大量的研究成果，多尺度结构不仅可以有效发掘材料的承载潜力，而且在多物理场应用中表现出更优异的属性，如减震吸能、隔热降噪等，为多尺度结构一体化设计在多物理场耦合领域和交叉学科中的应用提供了巨大的研究和应用前景。

2. 4 航空航天应用

材料结构一体化设计为高性能航空航天结构设计提供了坚实的理论基础。张卫红等针对材料结构一体化设计理论在航空航天领域的成果应用开展了大量研究。首先针对易受振动激励影响的卫星天线结构，基于模态加速度法提出了动力学拓扑优化方法，并进一步借鉴骨骼腔体仿生结构形式，拓展为结构拓扑-点阵仿生构型的协同优化技术，实现了宏观结构拓扑构型和点阵填充样式的匹配设计，如图5 所示，相比原有结构构型，动响应降低25%以上，减重17%以上。其次，针对某卫星平台，在保证固有频率大于50 Hz 的前提下，进一步将卫星设备组件布局集成到一体化设计模型中，在满足结构性能的基础上，实现减重32%的设计目标。另外，针对高速飞行器防热-承载一体化设计需求，提出了由耐高温陶瓷基复合材料层、轻量化隔热点阵层和金属加强筋结构组成的多层热防护系统，如图6 所示。并集成结构拓扑变量、点阵位置变量和点阵构型参数三种混合变量，对集成热防护系统进行一体化设计，点阵相对密度和构型与外部不均匀的热-机械载荷进行匹配设计，热防护效果提升了22.7%，应力降低了27%。

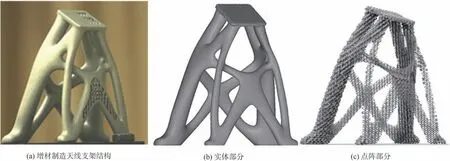
图5 点阵填充的卫星天线支架结构Fig. 5 Satellite bracket structure filled with lattice

图6 高超声速飞行器头锥多层热防护结构Fig. 6 Multilayer thermal protection structure for hypersonic aircraft nose cone

Wang 等［133］提出了实体-点阵混杂结构的优化方法，主要包含两个核心流程。首先采用基于实体各向同性材料惩罚模型（Solid Isotropic Material with Penalization， SIMP）的拓扑优化技术在给定设计空间内寻找最佳的材料布局形式，通过几何特征识别提取出最优承力路径，然后进行结构重构并区分出实体域与点阵填充域；其次采用点阵各向异性材料插值模型（Lattice Anisotropy Material with Interpolation， LAMI）在点阵填充域中寻找最优的单元相对密度分布场，然后依据各单元的相对密度值进行点阵结构填充，最后通过优化点阵结构中所有杆件的横截面积获得满足设计要求的多尺度实体-点阵混杂结构。基于该方法对整体式舵面结构进行设计，设计结果表明相比纯实体结构和纯点阵结构，刚度提升20.3% 和55.5%，如图7 所示［133］。 Zhou 和Geng［134］将参数化点阵设计与主动冷却流道设计相结合，基于代理模型实现了复合点阵单胞的热-机械性能快速表征，在优化过程中综合模拟热力耦合作用下的结构响应，有效平衡了复合点阵结构的承载性能与隔热性能。

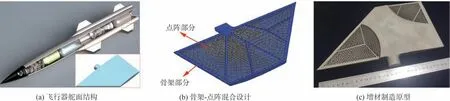
图7 舵面结构的骨架-点阵混合设计［133］Fig. 7 Skeleton-lattice hybrid design for rudder structure［133］

然而，基于密度法拓扑优化结果通常会产生锯齿状边界，在转化成三维模型时通常需要人工光顺，重构后的结构性能相比原有设计产生一定偏差，因此将优化设计结果直接转化为几何模型仍是限制工程应用的重要因素。基于此，Liu等［135］利用自适应B 样条拟合将优化结果转化为参数化CAD 模型。Jiu 等［136］应用特征驱动的拓扑优化方法直接对CAD 模型进行拓扑优化，避免了重构再设计过程。

3 展 望

面对新一代航天器技术发展对高性能结构件超强承载、极端耐热、超高精度和超轻量化的设计需求，充分利用增材制造技术的工艺优势，实现材料、结构、工艺、功能一体化设计是发展先进高性能航天结构的重要研究方向和发展趋势。未来值得开展的研究工作包括：

1）基于仿生思想、拓扑优化实现航天结构件的多功能、多学科设计。传统的刚度强度设计指标已无法满足航天器快速发展的需求，抗冲击性能、抗疲劳性能、热防护性能等指标，乃至声、光、热、电、磁等多领域功能需求对先进结构设计方法提出了新的挑战。基于此，Zhang 等［137］和Zhao 等［138］分别发展了基于疲劳性能约束下的拓扑优化方法，取得了良好的设计效果。Yang等［139］将拓扑优化技术拓展到热防护结构的设计应用中，基于多目标优化手段实现承载性能和防热性能的匹配设计。Chen 等［140-141］基于拓扑优化方法对隐身材料分布进行优化，有效提升了隐身材料的利用效率。然而，关于多学科、多功能结构优化技术研究工作十分有限，而且多物理场分析对计算时间和硬件的需求也使这些研究工作局限于二维结构。因此，结合机器学习等智能算法，发展基于多物理场下的高效结构优化技术，综合评估不同物理属性之间的内在耦合关系，是发展多功能、轻量化航天结构的重要途径。

2）发展现有材料所不具备的声光电热磁等物理属性的超材料，从微观尺度实现功能性结构设计。如隐身、降噪，防热问题一直都是飞行器设计面临的关键性问题，Yang 等［142］基于增材制造技术成功制备出了具有梯度特性阻抗指数的多层吸波超材料，与传统吸波材料相比有效提升了广角电磁波的吸收特性。Sun 等［143］提出了一系列基于六边形或kagome 子单元的分层蜂窝结构超材料，具有良好的窄频降噪效果。将拓扑优化技术应用于超材料设计，甚至与承载结构进行整体设计，在承受或传递载荷的同时具备隐身、降噪等传统材料无法具备的多功能特性，是未来高性能航天结构发展的新方向。

3）结构智能化和结构器件的一体化增材制造。通过智能材料如压电陶瓷、形状记忆合金等作为驱动元器件取代传统的机械传动方式，实现飞行器作动面的柔性变形，不仅具有变形灵活、系统简单等特点，而且实现了变形承载一体化的设计目标。Gu 等［144］基于形状记忆合金设计并优化了可精确变形控制的柔性机翼。Chen 等［145］基于压电复合材料实现翼梢小翼倾角自适应调整，提升气动性能。一方面，需要发展制备兼具响应速度快和大驱动载荷的智能材料，同时利用先进增材制造技术实现智能元器件与结构件的一体化成形。另一方面，为了达到精确变形的设计目标，需要发展作动元器件布局与主体结构构型的匹配设计方法，建立元器件与主体结构之间耦合的精确高效非线性变形评估和分析模型，同时解决智能变体结构系统的稳定性和可靠性问题。