2219-O 铝合金声软化效应建模与预测
2023-06-28李双利赵亦希于忠奇崔峻辉寇琳媛
李双利,赵亦希,*,于忠奇,崔峻辉,寇琳媛
1.上海交通大学 薄板结构制造研究所,上海 200240 2.宁夏大学 机械工程学院,银川 750021
大型带内筋薄壁筒形件是航天器中的主承力结构,由于2219 铝合金在室温下具有较高强度、良好的耐高温、耐应力腐蚀等特性,目前作为一种首选材料已广泛应用在带内筋薄壁筒形件旋压成形工艺中,但存在内筋填充高度不足等问题,这是由旋压过程中材料流动有限导致的,因此可借助外部能场辅助旋压改善成形过程中材料的塑性流动,实现更优的成形性能。现阶段超声能场已在金属的焊接、切削、铸造及成形等领域有广泛应用[1-4],但多数成形研究仅限于试验现象的分析,未对前述现象的内在机理进行详细分析。因此从声软化建模的角度解释超声振动辅助成形中的声软化现象,探究其内在机理,可实现超声振动辅助塑性成形技术更为有效的应用,尤其在2219-O 铝合金带内筋薄壁筒形件超声辅助旋压成形过程中,通过声软化效应模型的建立探明超声作用下铝合金在旋压过程中的内在成形机理,可为旋压成形过程中声软化效应的调控提供理论基础,对提高内筋的填充高度具有重要意义。
Blaha 和Langenecker[5]于1955 年首次对超声振动条件下锌拉伸变形进行了研究,他们在试验中发现超声振动的作用会导致屈服应力和流动应力大幅度降低。到目前为止,尽管对超声振动基本作用机理的研究存在很多不同观点,但普遍认为将超声振动加载到金属静态变形上可显著改善材料的塑性流动并降低成形载荷。近年来许多学者对声软化效应的机理进行了相关解释[6-7]。Abramov[8]研究了超声振动对材料微观结构和力学性能的影响,结果表明超声振动产生的应力作用在金属材料晶体中,当超过其屈服强度时位错密度会得到提高,进而发生位错排列,而位错可从超声振动中吸收能量降低流动应力。Dutta等[9]对有无超声振动的低碳钢样品的核平均取向差(KAM)和位错密度分布进行了X 射线衍射(XRD)和电子背散射衍射(EBSD)观测和对比分析,发现位错偶极子湮灭的增强导致位错密度的降低,超声振动使位错传播的行程增加从而提高了湮灭的概率。Siu 等[10]进行了铝超声振动加载压痕试验,通过EBSD 和透射电子显微镜(TEM)观测表明超声振动诱发材料发生软化效应,与具有不同层错能的金属中位错湮灭和/或亚晶粒的形成有关。
由以上的研究内容可知超声振动作用下材料的变形行为不仅与超声振动的振幅、频率及作用时间等工艺参数有关,还与晶体结构、位错密度等材料微观结构变化有关,这就使关于声软化效应的建模变得相对困难。Siddiq 和El Sayed[11]通过对传统晶体塑性理论的修正建立了一种唯象微观力学的材料模型,该模型考虑了变形过程中的声软化和热软化效应。Yao 等[12]基于晶体塑性理论提出了统一的声塑性模型解释声软化和残余硬化现象,该模型能准确预测铝试样在超声振动辅助镦粗过程中的应力-应变曲线。但这两种模型都只是基于宏观尺度的声软化效应建模,未分析超声振动对微观结构组织的影响。Wang 等[13]基于Bata 和Pereloma[14]的半物理Hall-Petch 模型提出了一种基于能量的模型,并通过EBSD、XRD 和TEM 分析了超声振动辅助微拉伸样品的织构演变、位错密度和位错分布,该模型在小应变下与试验结果较为匹配,但模型局限于静态某一点应变下的预测。
本研究主要通过建模和试验验证结合的方式研究2219-O 铝合金超声振动辅助拉伸过程中晶粒尺寸与流动应力之间的关系。首先建立与超声振幅相关的应变-晶粒尺寸的关系式,随后基于Hall-Patch 关系建立晶粒尺寸变化对应力-应变曲线影响的模型,使用粒子群(PSO)算法对参数进行识别,并通过不同超声振幅条件下2219-O 铝合金的拉伸试验及EBSD 微观结构组织观测验证模型的正确性。
1 模型描述
一般利用式(1)所示的Hall-Petch 公式描述晶粒尺寸d与屈服应力σy之间的关系:
式中:σo和Khp分别为晶格摩擦应力和Hall-Petch斜率。基于式(1),一些用于解释Hall-Petch 相关物理意义的假设得以提出,其中较为经典的有:① 相邻晶粒成核的滑移是由晶界的位错堆积引起的;② 晶粒发生屈服时位错密度与晶粒尺寸的倒数成正比;③ 基于统计模型,障碍物强度和障碍物间的间距对位错运动的影响决定屈服应力[15-18]。然而在描述这些假设时,由于相关参数难以测量,很难通过试验进行验证,尤其是引入超声能场辅助工艺后难以测量相关参数如临界应力、位错密度、障碍物强度及障碍物间的间距。因此以能量为基础明确解释Hall-Petch 斜率的物理意义,建立基于位错弹射机理的Hall-Petch模型,得到Hall-Petch 斜率Khp[13]:
式中:mT为泰勒因子;μ和b分别为剪切模量和Burgers 矢量的大小;h为位错间的间距,取决于晶界的性质,设ρgb是晶界处的位错密度,则可用表示;ρ为位错在晶粒内部的密度;λ为与晶界处位错密度相关的比例因子;Ko为初始能量因子,取Ko=1,对应螺旋位错,因为它们在超声激励下容易被激活[10];βK和nK为试验确定的参数;εinc为应变增量。
Wang 等[13]的模型是基于晶粒尺寸d不变的前提下的,然而在拉伸过程中晶粒尺寸d是在不断变化的,尤其在引入超声振动后超声能量的加入会使晶粒尺寸d发生相对更显著的变化。
因此考虑变化的晶粒尺寸在超声拉伸过程中对流动应力的影响,将晶粒尺寸d设为
式中:do为初始晶粒尺寸;Δd(i)为随应变变化而变化的晶粒尺寸。i为拉伸过程中的应变点,将变化晶粒尺寸与应变的关系设为
式中:s为与超声振幅相关的系数;ε为应变;l为应变指数。则变化的流动应力为
式中:ΔKhp(i)为Hall-Petch 斜率的变化量[13],其表达式为
式中:p和q分别为控制位错产生的系数和控制位错湮灭的系数[19];η为与位错密度和剪切应变相关的比例系数;β和n为与固定材料的内在金相性能有关的参数,是由试验决定的常数;εinc(i)为变化的应变增量;Euv为声能密度;ΔKrefhp为参考应变下的Hall-Petch 斜率的减少量;κ为比例因子,κ>1;r为晶界分数;K为能量系数,与局部障碍的强度相关联,可用剪切应变γ的唯象幂定律描述[19]:
声能密度可表示为[12]
式中:ξ和f分别为超声振动幅值和振动频率;ρFe为不锈钢变幅杆材料密度,ρFe=7.85 g/cm3;αv为声功率透射系数,表示为
式中:ρAl为拉伸铝合金试样材料密度,ρAl=2.84 g/cm3;cAl和cFe分别为超声在拉伸试样和变幅杆中的波速,。通过计算得声功率透射系数αv=0.374 0。因此在超声频率一定的情况下,根据式(10)可得不同超声振幅下的声能密度Euv,如表1 所示。

表1 不同超声振幅下的声能密度Table 1 Acoustic energy densities with different ultrasonic amplitudes
利用式(5)可将式(1)改写为
式中:σ(i)为拉伸过程中随Hall-Patch 斜率及晶粒尺寸变化的真应力,当i=1 时σ(1)=σin,其中σin为拉伸开始时由瞬时应变引起的初始瞬时应力,i的取值范围依据试验的应变数据点。
2 试验方法
2. 1 超声拉伸试验
如图1(a)所示,采用的超声发生装置主要由超声波发生器、超声波换能器及超声波变幅杆构成。超声波发生器的频率为20 kHz,频率可在较小范围内调整,最大输出功率为3 500 W。可通过更改超声波发生器输出功率占比进而改变输出振幅大小,试验最小振幅为3 μm,最大可实现振幅为9 μm。对设计的变幅杆结构进行模态分析,使其固有频率在工作频率附近,在超声拉伸的试验中为试样提供轴向方向的振幅。

图1 超声单轴拉伸试验设备Fig.1 Ultrasonic uniaxial tensile experimental equipment
图1(b)为超声拉伸测试设备。支撑座为圆柱形空心结构,能有效保证超声拉伸过程中的同轴度;由法兰盘固定的超声变幅杆及换能器嵌入圆柱型支撑座中,拉伸加载试验是在万能试验机上进行的。试验前试样的一端旋入变幅杆一端,另一端旋入连接夹具中,最后万能试验机的上端对连接夹具进行夹持固定。在超声振动拉伸过程中利用万能试验机的力传感器对过程应力进行测量,使用数字图像相关(Digital Image Correlation,DIC)系统测量过程应变。
2. 2 样品制备及处理
试样初始材料为2219 铝合金轧制板。为方便试样与超声变幅杆连接,试样加工为圆柱状且两端带有螺纹,试样结构尺寸及实物如图2 所示,先通过车削加工制备,套丝加工螺纹,再打磨测试段表面以降低表面粗糙度,最后利用SGL-1400 真空管式炉对试样进行完全退火热处理(退火温度为300 ℃,退火时间为120 min),消除材料加工过程中产生的加工硬化,保证材料最终处于O 态,具体化学成分如表2[20]所示。此外由于使用3D-DIC 测量应变,试样表面需喷涂散斑,如图2(b)所示。

图2 试样结构Fig.2 Sample structure
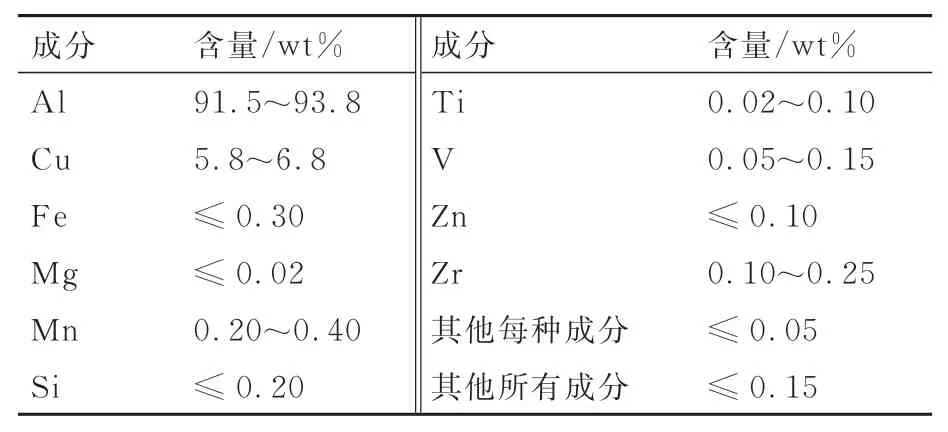
表2 2219-O 铝合金化学成分[20]Table 2 Chemical composition of 2219-O Al alloy[20]
2. 3 超声拉伸试验过程
为探究不同拉伸位移及超声振幅对拉伸过程中试样微观结构组织的影响,设置了不同的超声振幅(3、6、9 μm)及拉伸位移(1.5 mm(均匀塑性变形起始点)、3.0 mm(颈缩处)、拉断)。具体步骤如下:① 在不加超声振幅的条件下单向拉伸的位移分别为1.5 mm、3.0 mm、拉断,得3 种位移的应力-应变曲线,作为原始的对比;② 以相同的操作条件进行向上拉伸,施加不同超声振幅(3、6、9 μm)分别拉伸至相同位移(1.5 mm、3.0 mm、拉断)处,得到9 种不同状态下的应力-应变曲线。
2. 4 EBSD 观测
将2.3 节中超声拉伸试验后的样品沿拉伸方向利用电火花切割技术切下长度为10 mm 的半圆柱样品,采用MIRA 3 LMH 分析型高分辨扫描电子显微镜(SEM)和Oxford EBSD,在加速电压为20 kV 的条件下获得了晶粒的微观结构。用HKL CHANNEL5 软件处理,图3 为数据处理后的2219-O 铝合金初始微观结构组织EBSD 图,由于初始材料为2219 铝合金轧制板,且沿轧制方向加工得到试样结构,因此试样初始微观结构呈现沿轧制方向细长晶粒堆叠的特征,试样初始晶粒尺寸约为11 μm。

图3 2219-O 铝合金初始微观结构组织EBSD 图Fig.3 EBSD diagram of initial microstructure of 2219-O Al alloy
2. 5 显微硬度测试
对2.4 节中EBSD 观测后的样品进行显微硬度测试,所用LCD 型步进工作台图像分析自动转塔显微硬度计型号为HXD-1000TMJC,试样的测试面为EBSD 观测面,且为保证测试准确性,每个试样取10 个点测试并求平均值,得不同拉伸位移及不同超声振幅条件下试样的显微硬度。
3 结果与分析
3. 1 应力-应变曲线
图4 为2219-O 态铝合金试样在不同超声振幅下的拉伸应力-应变曲线,声场发生时间持续整个拉伸过程,拉伸直至拉断。由图4 可知在拉伸过程中,超声振幅的引入使试样所受应力始终小于相同应变下无超声状态时所受应力,这说明在超声振动加载的过程中试样始终受声软化效应影响。不同超声振幅条件下2219-O 铝合金具体的材料特性如表3 所示,可见随超声振幅增加材料的屈服强度逐渐降低,即声软化效应逐渐增强,这与之前研究显示的趋势一致[21]。由表1 可知超声振幅越大,声能密度越高,更多的能量作用在拉伸过程中,试样因此在宏观层面表现出更明显的声软化效应,但为进一步探究超声能量作用于拉伸过程的机理,还需对其微观内在机理进行分析。

图4 不同超声振幅下的单轴拉伸应力-应变曲线Fig.4 Uniaxial tensile stress-strain curves with different ultrasonic amplitudes

表3 不同超声振幅下2219-O 铝合金材料特性Table 3 Material properties of 2219-O Al alloy with different ultrasonic amplitudes
3. 2 EBSD 及显微硬度测试结果分析
3.2.1 拉伸位移对晶粒尺寸的影响
由图5 可知晶粒的平均尺寸会随拉伸位移的增加而增大。当不施加超声振幅时,随拉伸位移从1.5 mm、3.0 mm 增加至拉断,晶粒的平均尺寸分别为10.502、15.657、21.630 μm;当超声振幅为6 μm 时晶粒的平均尺寸分别为16.726、20.751、28.175 μm。这意味着拉伸位移的增加可在一定程度上促进晶粒尺寸的增大。这是由于拉伸位移的增加使应变逐渐增加,根据式(4)可知应变的增加会导致随应变变化的晶粒尺寸变化量增大,从而使式(3)中晶粒尺寸增大。
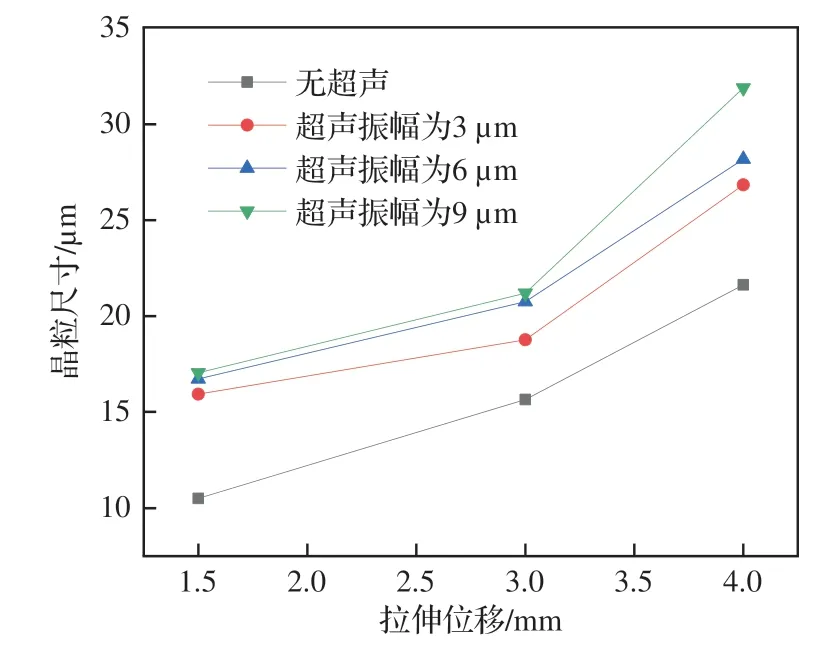
图5 单轴拉伸位移与晶粒尺寸的关系Fig.5 Relationship between uniaxial tensile displacement and grain size
3.2.2 超声振幅对晶粒尺寸的影响
图6 为拉伸过程中超声振幅与晶粒平均尺寸的关系。以拉伸位移3.0 mm 为例,不加超声振幅拉伸后的晶粒平均尺寸为15.657 μm,而在超声振动条件下随施加超声振幅增大(3、6、9 μm),其晶粒尺寸分别为18.771、20.751、21.186 μm。这说明加入超声振幅会引起晶粒尺寸增大。同时这种趋势也表明超声能量可在一定程度上抵消加工硬化对晶粒尺寸的限制,使晶粒尺寸比未超声振动的晶粒尺寸增大更明显。根据式(6)可知,超声能量的增加使ΔKhp(i)的变化量逐渐降低,同时晶粒尺寸的变化量Δd(i)逐渐增大,从而使式(5)中应力的变化量Δσ(i)逐渐降低。因此在相同拉伸条件下,材料的软化效应随超声振幅的增加而更加明显,呈现出与图4 相同的趋势,即流动应力随超声振幅的增大而降低。由图4 计算可知超声振幅每增加3 μm,平均流动应力降低约6.5%,这说明超声振幅的增加在一定程度上促进了金属塑性成形过程中的材料流动。

图6 超声振幅与晶粒尺寸的关系Fig.6 Relationship between ultrasonic amplitude and grain size
3.2.3 超声振幅对显微硬度的影响
为进一步说明超声振幅在拉伸过程中对材料软化效应的影响,对试验后的样品进行了显微硬度试验(原始样品硬度为120 HV)。图7 为所得样品的硬度,可见随拉伸位移增加,材料硬度降低的趋势愈加明显,且在相同拉伸位移条件下随超声振幅增加,材料硬度降低。
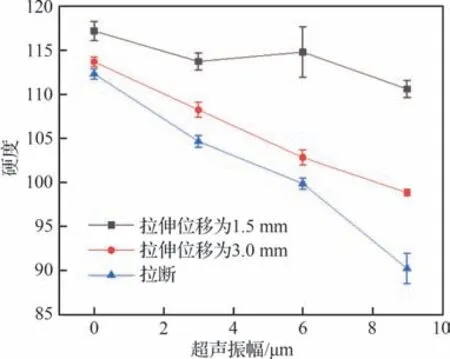
图7 超声振幅与显微硬度的关系Fig.7 Relationship between ultrasonic amplitude and microhardness
通过硬度测试进一步说明了拉伸位移及超声振动对材料软化效应的影响。在拉伸过程中由于超声振动能量的叠加,试样晶粒尺寸出现适当的增大,因此降低了试样的显微硬度。此外试验后样品显微硬度测试表现出的趋势也可对超声振动拉伸试样的声残余软化效应[22]进行相应的解释与说明。
3. 3 参数识别与模型验证
一些基本参数可通过文献和公式计算得到,其他参数可通过将模型公式与2219-O 铝合金的拉伸试验曲线进行拟合确定。得到相关参数后通过模型进行预测,并与试验结果进行比较。
采用3 种不同超声振幅的拉伸试验识别材料参数,模型参数拟合最常用的方法是最小二乘法,但当模型参数较多时往往迭代次数过多,容易陷入局部最优解的情况,而粒子群(PSO)算法具有收敛速度快、参数少、算法简单易实现的优点,且对于高维度优化问题比遗传算法更快收敛于最优解。需拟合识别的参数有16 个,参数较多,因此利用PSO 算法进行曲线拟合,其拟合过程如图8 所示,PSO 算法最大迭代次数为100,每隔50 代输出一次,粒子数设为20,学习因子为2,初始惯性权重为0.9,结束惯性权重为0.4,最小全局误差为1×10-6,采用针对被优化目标函数的优化型适应度函数,粒子维数为16。

图8 PSO 算法流程图Fig.8 Flow chart of PSO algorithm
通过查阅文献得式(2)中的参数mT、b及式(7)、式(8)中的参数r[23],由ρgb=κρ[13]可得式(7)、式(8)中的比例因子κ。
根据3 种超声振幅条件(3、6、9 μm)拉断状态下的试验应力-应变数据参数识别得到其他参数,并在如表4 所示的模型参数中进行标注,其中s作为与超声振幅相关的系数会随超声振幅的改变发生变化,上标*代表需要进行参数识别得到的参数。

表4 2219-O 铝合金模型参数值Table 4 Model parameter values for 2219-O Al alloy
参数识别得到的不同超声振幅下应力-应变曲线与对应试验曲线拟合如图9 所示,并对数值拟合数据与试验数据进行误差计算,当超声振幅为3、6、9 μm 时模型与试验结果的平均误差分别为8.0%、4.0%、6.7%。因此模型计算结果与试验结果具有较高的一致性。
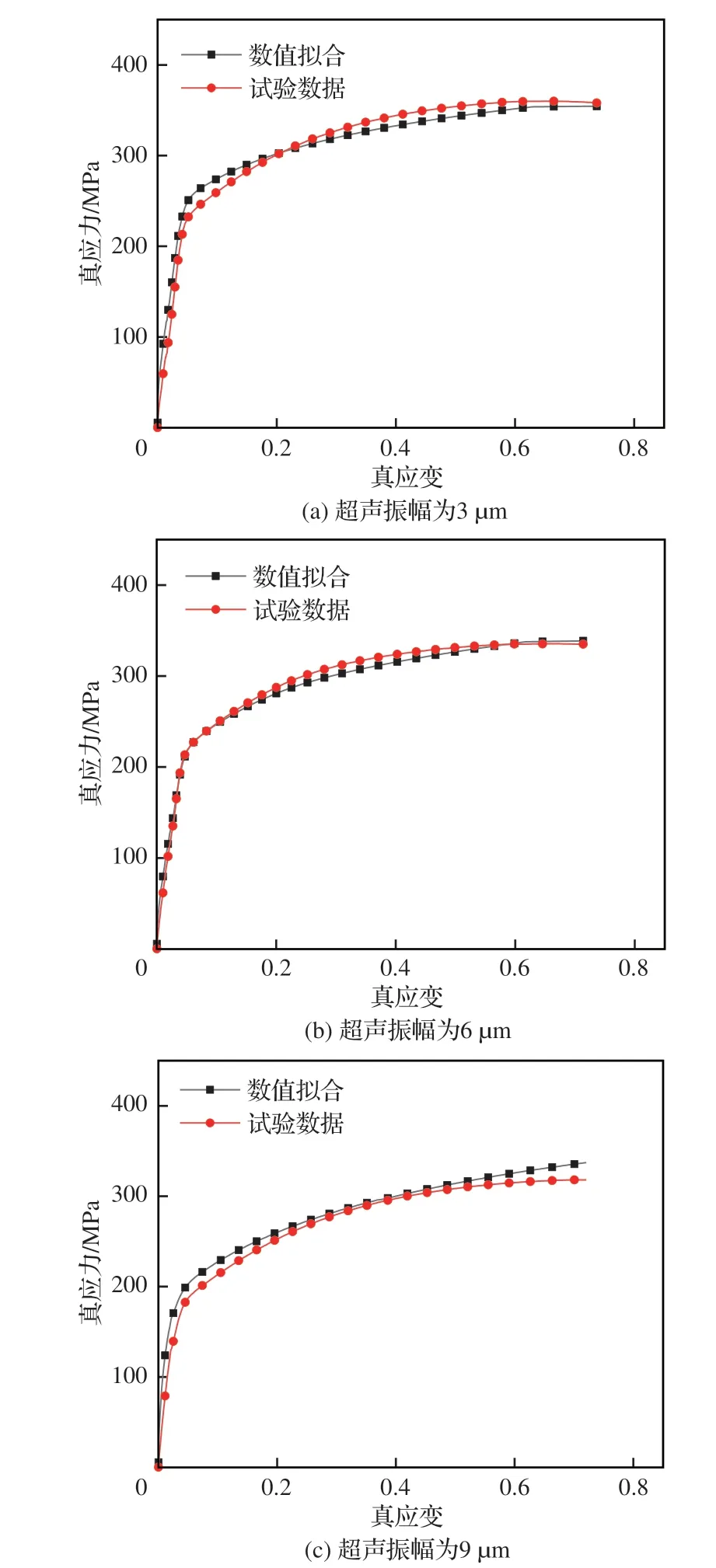
图9 参数识别得到的应力-应变曲线与试验曲线拟合Fig.9 Fitting of stress-strain curves obtained by parameter identification to test curves
为验证表4 中参数的准确性,利用识别出的参数进行3 种超声振幅下拉伸1.5 mm 及3.0 mm的模型计算并与相应试验数据对比,且每组模型计算重复多次,其中的两组(超声振幅为3 μm、拉伸位移为1.5 mm,超声振幅为6 μm、拉伸位移为1.5 mm)对比结果如图10 所示,可见预测与试验结果吻合较好,表明了模型计算的准确性,对于拉伸过程中的声软化效应可进行较为精确的预测。

图10 模型参数验证Fig.10 Validation of model parameters
利用建立的模型对不同超声条件下拉伸的应力-应变曲线进行预测,选择超声振幅为12 μm和15 μm,预测至颈缩状态过程中的应力-应变曲线。根据式(4)可知晶粒尺寸的变化与应变相关,因此预测的应力-应变曲线中应变采用超声振幅9 μm 颈缩试验中的应变数据。预测的曲线如图11 所示,随超声振幅增加拉伸过程中的应力逐步下降,声软化效应愈加明显,这与图4 中试验结果表现出的趋势是一致的,此外超声振幅每增加3 μm,由于声软化效应导致的应力下降约6.5%,同样与试验结果较为一致,因此建立的模型可对一些试验无法实现的高超声振幅条件下拉伸过程的声软化效应进行分析预测。
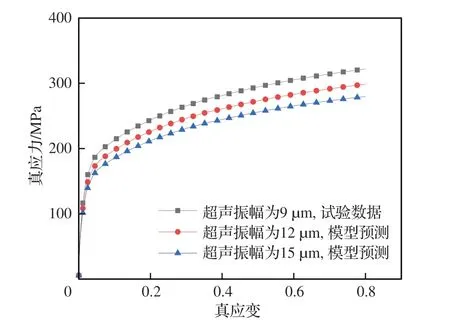
图11 预测得到的高超声振幅单轴拉伸过程的声软化效应Fig.11 Predicted acoustic softening effect during uniaxial tension with high ultrasonic amplitude
4 讨 论
过去的研究表明塑性变形的本质是位错滑移,而这种滑移的形成是基于能量吸收的[22-26]。在拉伸试验过程中拉力的施加会为位错的滑移提供能量,而超声振幅的引入作为一种能量源,在塑性变形整体所需能量不变的前提下,超声能量的加入势必会降低拉应力的大小,因此在整个拉伸过程中若超声能量持续存在,则与未加超声振幅相比拉伸所需的拉应力较小,且拉应力的大小与超声振幅大小成反比,如图4 所示,这从宏观层面上对声软化效应的作用机理进行了解释。
在微观层面上,通过对不同试验条件下样品的EBSD 观测发现在拉伸过程中,晶粒的平均尺寸会有一定变化,如图12 所示,这种现象在一定程度上会对拉伸过程中应力的变化造成一定影响。因此对EBSD 图进行处理,得不同试验条件下晶粒平均尺寸的变化,如表5 所示,可见随拉伸位移增加,晶粒平均尺寸会略有增大。从位错变化机理的角度分析,拉伸位移增加引起应变增大,机械能传递进入到材料内部被晶粒吸收,这提高了材料跨越障碍的能力,位错增殖因而降低,同时位错湮灭的概率增加[21],造成晶界处的晶界能降低,导致晶粒尺寸增大,然而随拉伸位移增加材料会出现硬化现象,即塑性变形引起位错储存,阻碍了位错湮灭和位错弹射的发生[13],因此晶粒尺寸的增大受限制。而超声波的加入可补充材料克服障碍所需的能量,从而在一定程度上抵消拉伸过程中出现的硬化,这与超声振幅变化有关。
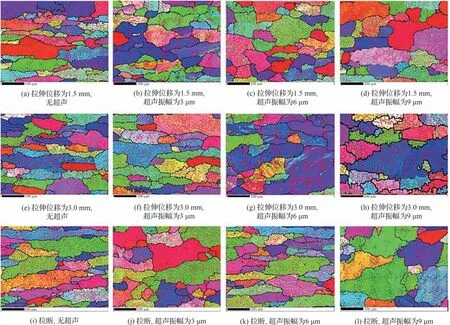
图12 不同试验条件下样品的EBSD 图Fig.12 EBSD diagrams of samples with different experimental conditions

表5 不同试验条件下的晶粒尺寸Table 5 Grain sizes under different experimental conditions
随超声振幅增大,晶粒尺寸也呈现出更为明显的增大趋势,如表5 所示。这种现象可通过超声振幅的增大可促进晶界处位错密度的降低解释。此外由于超声振幅还会增大晶界处位错湮灭的概率,两者导致晶界处的晶界能较无超声状态下降得更多,而晶粒长大的驱动力是晶界能的下降。因此在相同应变条件下,随超声振幅增大晶粒尺寸也随之增大。
基于模型预测得到的不同超声振幅条件下晶粒尺寸随应变增大而变化的趋势与试验结果基本吻合,如图13(a)所示(初始晶粒尺寸设为10 μm)。这不仅验证了所建模型的正确性,也表明了晶粒尺寸的增大可有效解释超声拉伸过程中出现的声软化效应。

图13 预测得到的晶粒尺寸与应变的关系Fig.13 Relationship between predicted grain size andstrain
图13(b)为超声振幅9 μm 条件下模型预测结果与试验结果对比,在相同应变处超声拉伸试验样品的晶粒尺寸与模型预测的晶粒尺寸较为吻合,超声振幅3、6、9 μm 条件下模型预测结果与试验结果的对比误差分别为5.6%、6.8% 及6.6%。这说明建立的模型可较为精确地阐明在超声拉伸条件下晶粒尺寸随应变增大的变化趋势,同时进一步证明了在超声拉伸过程中会出现晶粒尺寸增大,从而引起声软化效应。
5 结 论
通过数值模拟和试验对比的方法研究了2219-O 铝合金在超声拉伸过程中出现的声软化效应。基于Hall-Petch 效应建立了与超声振幅相关的声软化效应模型,利用PSO 粒子群算法进行模型参数拟合,通过超声拉伸试验验证了所建模型及拟合参数的正确性,利用所建模型预测了高超声振幅拉伸过程的声软化效应,对于数值模拟超声辅助金属塑性成形过程具有一定的参考意义,研究得出的结论如下。
1) 基于Hall-Petch 理论,考虑超声引起的晶粒尺寸动态变化可反映材料在超声辅助下的变形行为,从而定量计算超声作用下的软化效果。针对复杂的未知参数,在建立模型的过程中采用粒子群优化算法可很好地解决参数拟合问题,获得的模型与试验结果具有较好的一致性。
2) 对显微结构组织的EBSD 观测发现超声辅助单轴拉伸过程会导致晶粒尺寸增大,其增大的程度与超声振幅的大小成正比。预测得到的晶粒平均尺寸随应变的变化同EBSD 观测结果基本吻合,且与试验观测结果相比,所建立的关系式可动态反映晶粒尺寸随应变的变化,同时通过微观观测及模拟结果说明超声拉伸过程中声软化效应可一定程度上从微观晶粒尺寸增大的角度进行解释。
3) 通过研究预测得到的高超声振幅(9~15 μm)拉伸过程声软化效应发现超声振幅每提高3 μm,相同应变条件下拉伸应力下降约6.5%,与试验结果表现出的趋势一致,可为模拟超声辅助2219-O 铝合金塑性成形的定量研究提供理论基础。
