发动机泵后模拟供应系统频率特性的液流激励试验

董蒙，谭永华，何闯，邢理想，赵瑞国

1．西安航天动力研究所 液体火箭发动机技术重点实验室，西安 710100

2．航天推进技术研究院，西安 710100

在液体火箭发动机工程研制过程中，经常会出现大量系统级的稳定性问题。其中，推进剂供应系统与燃烧组件耦合稳定性问题在系统级振荡中表现突出［1-2］。系统稳定性与频率特性息息相关，针对发动机中供应系统与燃烧组件的稳定性问题，学者们常从频率特性角度完成理论研究［3-5］。频率特性重点关注各环节的幅相频率特性，结合稳定性判据，可评判发动机闭环系统稳定性。例如，美国ROCCID 软件结合分析理论和经验数据，利用频率特性曲线与频率稳定判据给予发动机稳定性评价［6-7］。Casiano［5］则利用频率特性与Nyquist 稳定性判据分析系统稳定性。可见，发动机局部或整机系统频率特性研究是发动机稳定性研究的基石。针对发动机频率特性理论研究，刘上等［4］对燃气发生器、煤油副路供应系统以及液氧供应系统的频率特性进行了深入探索。何闯［8］与张淼［9］等则分别研究了发动机入口处预压涡轮参数与燃气冷凝掺混对液氧供应系统的影响。李斌等［10］通过矩阵模块组装，分析了液氧煤油发动机整机的低频特性。

一般，采用液流激励试验系统完成系统或组件的频率特性试验研究。目前液流激励试验中使用的人工激励器有转盘式、转子式、活塞式、高速开关阀。其中，转盘式激励器因其结构简单，输入功率较低，在液流激励试验中普遍使用。学者们利用转盘式脉动激励器开展了一系列频率特性试验研究。最早，Bazarov 等［11-12］针对喷嘴动力学频率特性开展了试验研究，设计了一种转盘式脉动激励器。Chung［13］、富庆飞［14-15］等利用同类型的脉动激励器，得到喷嘴的动力学响应特性，并分析了结构参数对喷嘴频率响应的影响。薛帅杰［16］、李佳楠［17］等利用转盘激励器分别开展了敞口离心喷嘴、直流撞击式喷嘴的动力学特性试验，并利用高速相机展示了受迫扰动下的雾化响应。然而，转盘式激励器也有其固有缺点，即产生的脉动信号受液流试验系统的上游影响较大。为解决此问题，文献［18］采用支路贮箱单独供应的方式，利用近乎汽蚀的节流圈保证主路与激励系统的隔绝。这种系统设计的优点是激励源受主路的影响较小，便于试验数据处理，缺陷是不适用于激励引入处压力较高的试验系统。

上述系统皆是基于喷嘴动特性研究的组件级试验，不需要考虑整个激励系统边界对组件的影响，当重点关注系统级频率特性，便需要能够相对准确地模拟边界条件。刘上等［18-20］利用转盘式激励器产生了最高频率为1 200 Hz、最大幅值为1 MPa 的脉动压力［19］，并分别开展了针对泵后供应系统以及汽蚀管-管路系统的动态特性研究［18，20］，重点考虑了闭端边界条件的模拟，但由于此装置压降过高，产生的汽蚀效应大大增加了出口柔性，最终形成了与预设相反的声学开端边界［18］。对于系统频率特性研究中的闭端边界模拟，文献［21］中描述了一种节流短管与整流栅结合方式的闭端装置。利用入口与出口处的截面变化及整流栅压降损失增加流阻，利用细管增加流感，整体达到增加阻抗的目的。然而，根据该专利设置原则设计的闭端装置模型只对中高频波动具有较好的阻隔效果，由于低频段波长较长，穿透性强，声学闭端装置在低频段的闭端效果较差。

综上可见，目前，学者们对发动机系统的频率特性理论研究较多，相应的试验研究有所欠缺，表征系统真实特性的试验工作亟待开展。再者，上述学者们开展了低压工作状态下系统频率特性试验研究，本文液流激励系统背景环境为高压状态，在各组件结构承压能力限制下，液流激励系统需能产生足够的脉动信号，且需准确模拟边界条件，根据试验结果评估液流激励系统。

1 试验原理

1. 1 试验系统

对于高压补燃液氧煤油发动机系统而言，实际泵后供应系统如图1 所示。流量调节器所在流路环境为：上游是燃料二级泵，下游是燃气发生器［22］。由于真实产品的加工复杂性以及真实产品对试验辅助系统要求的严苛性，一般在地面试验中采用模拟手段研究该真实系统的频率特性。节流圈与流量调节器同属于节流组件，文献［23］研究了流量调节器-管路系统与节流圈-管路系统频率特性的区别，调节器与节流圈对频率特性的影响体现在幅值，当频率较低时，调节器系统幅值小于节流圈系统的，当频率较高时，则反之。然而，各阶谐振频率由系统决定，两者之间的差别不大。因此对于反映供应系统整体频率特性而言，可采用节流圈模拟调节器进行分析，并在系统设计时，保证两者的阻抗2Δp/qv（Δp为稳态压降；qv为体积流量）相同。实际发动机系统中预燃室压力较高，由于实际系统与模拟系统重点关注脉动量，稳态压力是通过作用于阻抗而影响频率特征，即实质上影响频率特性的特征参数为阻抗，而非单纯的稳态压力量。因此当稳态压力不是主要影响因素时，一般皆采用低压试验系统模拟实际压降和流量。例如，在同类的发动机液流激励试验中，学者们利用稳态压力较低的脉动激励器模拟高压热力组件的振荡［16-17，20］。

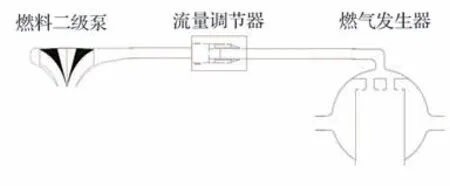
图1 实际泵后供应系统示意图Fig. 1 Schematic diagram of real feed system after pump

模拟准则为：① 介质模拟，试验介质为水，真实介质为煤油，水通过密度和声速换算可模拟真实煤油介质。② 结构模拟，将该液流激励系统的管路长度与真实系统保持一致，调整管路直径以保证两系统管路特征阻抗相同。③ 工况模拟，在保证阻抗相同的情况下，根据水和煤油的密度关系，将煤油质量流量工况换算为水，通过调整孔径达到模拟不同工况的目的。④ 激励边界模拟，燃气发生器中推进剂燃烧在供应系统出口产生宽频扰动波，可认为是激励源，利用激励器扫频模拟宽频扰动信号，引入了幅值与燃气发生器同等量级的相对脉动压力p′input/pˉinput（p′input和pˉinput分别为输入的脉动压力与稳态压力），扫频范围覆盖真实发动机系统出现的频率。⑤ 闭端边界模拟，燃料二级泵属于离心泵，泵叶片高速旋转使流体压力大幅提升，下游供应管路中扰动压力波传播至叶片处时，大部分会被离心泵叶片反射回来。此外，流体通过泵时压升很高，由此带来的泵端阻抗（（6.32～7.93）×109Pa·s·m-3）远大于管路特征阻抗（7.13×108Pa·s·m-3），下游的压力扰动波大部分被反射而不易传播至上游。因此二级泵端可认为是硬声场反射边界，即声学闭端，利用声学闭端装置模拟，即二级泵端与声学闭端装置处脉动压力p′处于流路的波腹位置。

根据模拟准则，表1 给出了两系统的设计参数对比（需要说明的是，由于介质不同，表1 中阻抗表示为脉动压力与脉动体积流量之比；本文其他地方阻抗均以水为介质，表示为脉动压力与脉动质量流量之比）。在模拟供应系统与真实系统中，试验件阻抗与主管路特征阻抗保持一致；对于泵端（闭端）阻抗、激励脉动压力与稳态压力之比以及频率范围，模拟供应系统涵盖真实供应系统的参数包络。

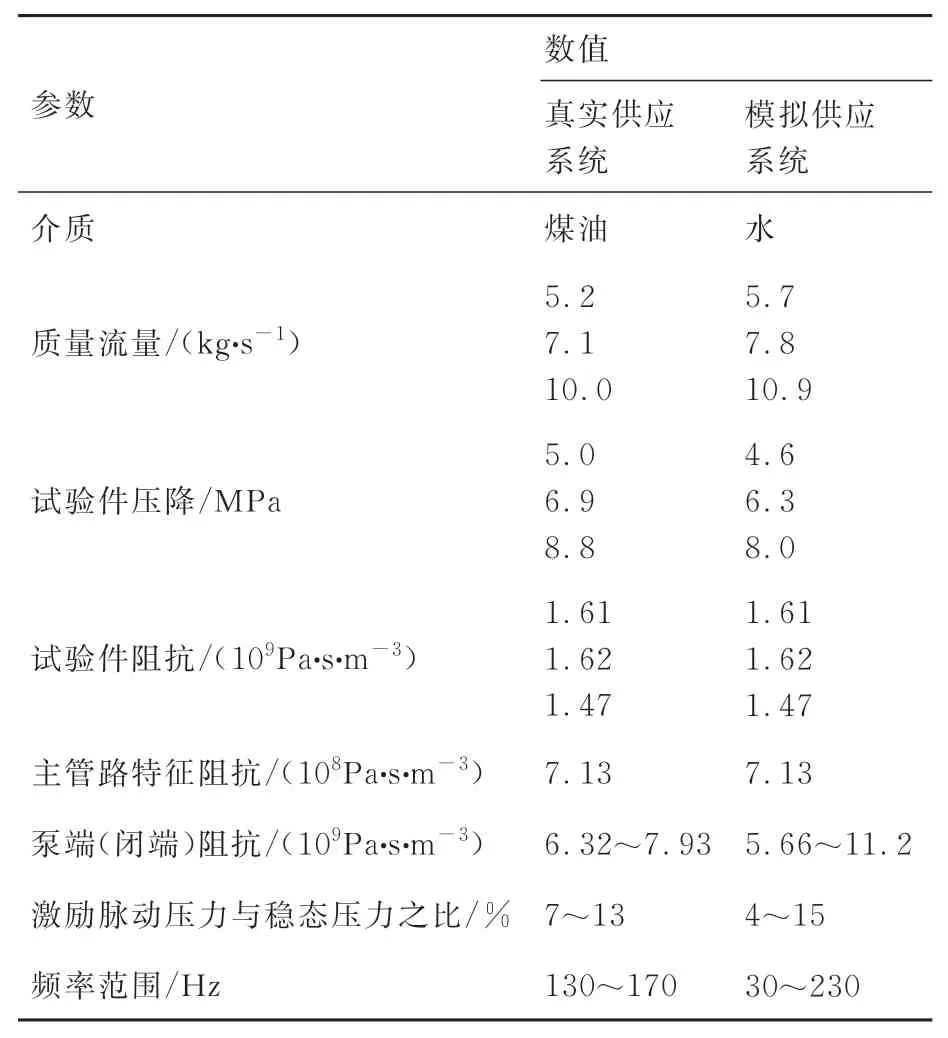
表1 真实供应系统与模拟供应系统设计参数对比Table 1 Comparison of design parameters of real feed system and simulated feed system

根据上述相似模拟准则，该液流激励系统与实际发动机泵后系统的结构参数、工况参数保持一致，并保证了闭端边界与激励边界模拟的相似性。液流激振试验系统如图2 所示，对应的实物见图3。试验介质为水，由贮箱6 供应。利用声学闭端装置1、激励器5 和节流圈2 分别模拟真实系统中的燃料二级泵、燃气发生器和流量调节器。其余节流圈用于调整系统压力，并可通过调整节流圈孔径改变主路流量，从而创造不同稳态流量和压力的工况条件。试验系统最高模拟压力为29 MPa，流量为40 kg/s。

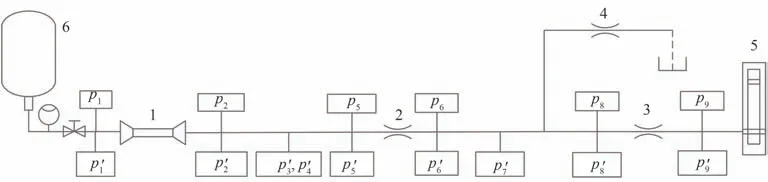
图2 试验系统原理图Fig. 2 Schematic diagram of test system

图3 试验系统照片Fig. 3 Photos of test system

本试验所用的激励器为转盘式激励器，激励器内转盘转动会周期性切断流入激励器的流量，在激励器路产生脉动压力，通过三通向上游传播。可以通过调整转盘孔径与个数分别控制脉动压力幅值与所能达到的最高激励频率，试验中通过调节电压控制电机带动转盘转动的速度，从而改变激励频率。采用2 种转盘孔径的激励器测试激励水平，分别为66×∅4 mm 和44×∅6 mm，其中转盘直径为170.6 mm，电机输出电压范围为0～ 5 V，精度为±5 mV。

试验中主路管道内径为∅50 mm，激励路管道内径为∅20 mm。主路节流圈2 孔径随工况变化，分别为∅9.9 mm、∅9.6 mm、∅8.9 mm，其中对应的设计工况流量分别为10.9、7.8、5.7 kg/s，节流圈3 孔径有∅5.3 mm 和∅7 mm这2 种尺寸。试验系统中共布置9 个脉动压力测点，6 个缓变压力测点，其中脉动压力传感器的采样频率为20.48 kHz，缓变压力传感器在30 MPa压力下的测量精度为±0.5%。声学闭端装置入口和出口分别布置脉动压力测点p′1和p′2，节流圈2 前后分别布置测点p′5和p′6，节流圈3 前后分别布置测点p′8和p′9。在闭端装置与节流圈2 之间沿程增布2 个测点p′3、p′4，在节流圈2 与三通之间增布一个测点p′7。系统从入口到激励器沿程缓变压力测点分别为p1、p2、p5、p6、p8、p9。

稳态流量与压力利用缓变参数表征，在不同入口稳态流量（qm）工况下，试验系统流路实测稳态压力（pi，i=1，2，6，9）如表2 所示。

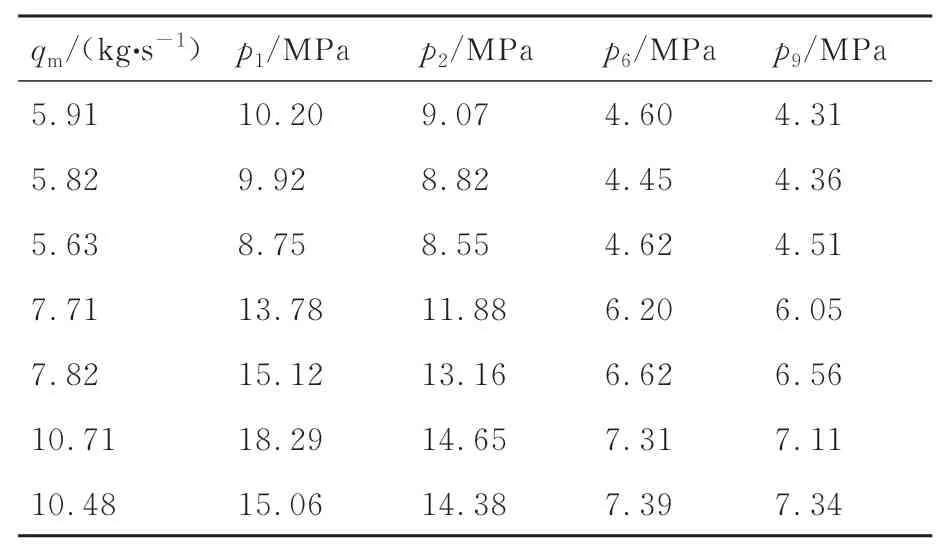
表2 不同流量工况下系统稳态工作压力Table 2 Steady-state working pressure of system under different flow conditions

1. 2 数据处理

频域的幅值和相位由原始时域脉动压力数据经傅里叶变换处理得到，由于激励信号频率是随时间变换的非平稳信号，因此采用短时傅里叶变换进行数据处理。脉动压力传感器采样频率为20.48 kHz，比最高研究频率1 kHz 的2.5 倍高，因此满足奈奎斯特采样定律，可保证整个研究频带无混叠。连续信号的短时傅里叶变换公式为

式中：t为时间；f为频率；x为原始时域信号；h为时间窗函数。

在实际计算机处理时，用到离散短时傅里叶变换，公式为

式中：k为离散时间步；N为采样总数。

进而，可得到各个时间点下的频谱为

式中：A为幅值；φ为相位。

最终，在每个时间点下，取频谱幅值最大点Amax（f1，k）、该点对应的频率f1以及该频率下对应的相位φ（f1，k），最终得到该时间点下的幅相频关系。

对采集的时域数据进行短时傅里叶变换时，选择时间窗长为1 s，时间增量为1 s，重叠率为0，频谱幅值采用RMS（Root-Mean-Square）格式。当时间窗取为1 s，频率分辨率为1 Hz，在数据分析范围内精度足够。为使时域信号满足傅里叶变换的周期性要求，减少频谱泄漏，对时域数据进行加窗处理，Hanning 窗具有较小的主瓣宽度，频率分辨能力较高，对时域信号叠加Hanning 窗，获取试验系统中脉动压力的时频数据结果。对于该液流激励系统而言，由于流体流动或声学系统固有的非线性，易激起人工激励频率之外的倍频或固有定频。图4 展示了压力脉动测点的色谱图，从图可见，在一个时间窗内可清晰识别出人工激励频率，其幅值较大，但同时也可能存在呈放射状的其他频率，但幅值较小。由于真实的水力激振系统为分布式的非线性系统，在外界施加激励条件下，系统除了在人工激励频率处有较大响应之外，确实表现出倍频特征。因此，每一帧的幅频图可能会对应多个突频，由于数据分析时重点关注人工激励频率下的响应特性，为防止其与非人工激励频率特性混杂，在时频色谱图人工激励突频附近添加阈值线。在阈值范围内进行寻找最大幅值操作，最终得到幅频响应曲线。进而，找到每一帧最大幅值对应的频率以及该频率处的相位，便可得到相频曲线。

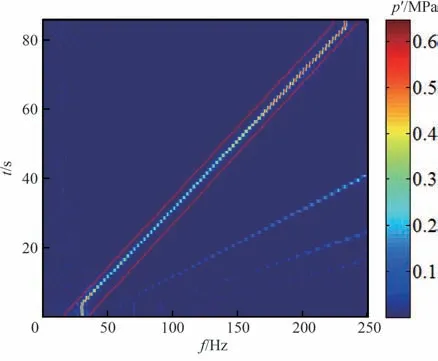
图4 压力脉动时频色谱图Fig. 4 Time-frequency chromatogram of pressure pulsation

2 试验结果

2. 1 激励水平

对于被试件而言，液流激励试验频率特性研究关键在于脉动信号的大小和品质。激励器转盘孔的遮盖与导通，产生类似开关阀的周期性水击效应，从而产生流量和压力脉动。试验中共研究了∅4 mm 和∅6 mm 这2 种转盘孔径对激励水平的影响，结果见图5。当激励器的转盘孔径为∅4 mm 时，流量工况为10.48 kg/s，激励器处稳态压力为7.34 MPa，脉动压力分频值为0.1～0.7 MPa，脉动压力与稳态压力之比为1.36%～9.54%。激励器的转盘孔径为∅6 mm 时，流量工况为10.71 kg/s，激励器处稳态压力为7.11 MPa，脉动压力分频幅值为0.3～1.07 MPa，脉动压力幅值与稳态压力之比为4.22%～14.77%。为了使代替试验件的节流圈2 处产生幅值大小合适的脉动信号，考虑到流体管路激励路传播至主路过程中，激励路节流圈和流体黏性对脉动信号的衰减作用，以及排放路的存在使得高频信号幅值大大降低这两方面因素，选择能产生较大压力脉动幅值的∅6 mm 转盘激励器为宜。

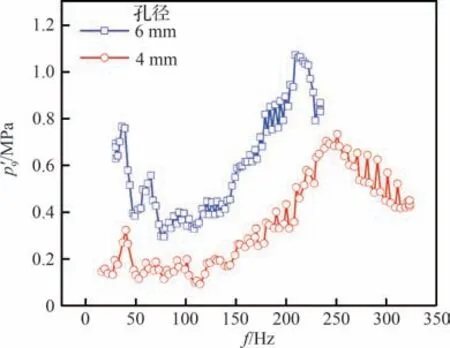
图5 转盘孔径对激励水平的影响Fig. 5 Influence of turntable aperture on excitation level

在选择∅6 mm 转盘的激励器作用下，液流激振系统主路和激励路产生的压力脉动时域曲线如图6 所示，稳态流量为10.71 kg/s。其中，激励路压力测点p′9接近激励源，产生较大的压力脉动，当脉动压力传播至主路（即测点p′6）时，脉动压力有所减小。在50、100、150、200 Hz 附近，激励源处分别产生大约峰峰值为1.25、1.50、2.50、2.80 MPa 的压力脉动，随着频率增加激励源产生的脉动压力幅值也增加，此频率反映了激励路部分子系统的频率响应特性。在各个频率段，激励出主路的脉动压力幅值峰峰值基本维持在0.8～1.0 MPa，说明高频段压力脉动传至主路时衰减较大。在50 Hz 时，激励路激励源处脉动压力波峰和波谷分布均匀，波形较好。从100 Hz 开始，由于倍频信号的叠加，波形呈现出上宽下窄的特征，从图4 也可见随着时间变化，参数明显表现出人工激励频率之外的倍频特性。由于激励路传播至主路时，高频段脉动压力衰减较为明显，因此主路参数倍频信号能量也大幅衰减，在各个频率段都表现出较为规整的波形。此外，在研究频率范围内人工激励主频可较为明显地分辨出来，本文重点关注人工激励频率下的系统响应特性，数据进行傅里叶变换后可辨识出人工激励频率以及对应的幅值相位，倍频及杂波信号的存在只影响人工突频的能量，不影响人工激励的频率，理论分析时可直接应用线性频域理论模型及相关结论。

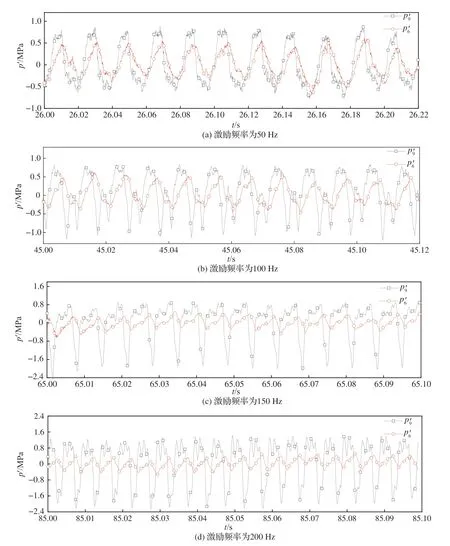
图6 主路和激励路压力脉动时域数据Fig. 6 Time domain data of pressure pulsation in main circuit and excitation circuit

由于人工激励倍频、非线性系统固有的定频、流体噪声存在以及脉动信号周期性截断的影响，各测点分频幅值较时域幅值具有较大差别。图7 给出了不同流量工况下的激励水平加窗短时傅里叶变换分频值，其中，在50、100、150、200 Hz附近，分频幅值在时域幅值中的占比为60.8%、46.0%、44.8%、61.4%，平均占比53.25%。为研究不同稳态工况对激励水平的影响，对比了3种稳态流量不同的工况，稳态压力也相应变化，分频结果如图7 所示。在3 种主路流量分别为5.82、7.71、10.71 kg/s 的工况下，激励器前稳态压力分别为4.36、6.05、7.11 MPa，对应的激励路稳态流量分别为0.41、0.53、0.65 kg/s。可见，随着主路稳态流量的增加，激励幅值增大，且特征频率保持不变。此外，从图7 中主路流量为10.71 kg/s 与7.71 kg/s 的曲线可见，稳态流量对谐振频率影响较小，但稳态流量较大时，系统更易表现出谐振特征。从图7 中可见，当流体稳态流量极小时，激励出的脉动压力幅值本身较小，且由于流体噪声、高频衰减等因素影响，使得激励源处特征频率被淹没。

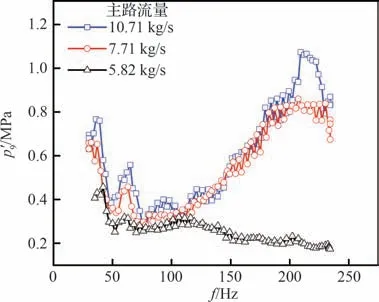
图7 流量工况对激励水平的影响Fig. 7 Influence of flow conditions on excitation level

进一步分析稳态压力与稳态流量对激励水平的影响。激励器前稳态压力由主路和激励路节流圈3 共同调节，激励路稳态流量的调整是通过节流圈3 完成，考虑单因素影响，保持主路节流圈不变，改变节流圈3 孔径以研究稳态流量和压力的影响。图8 给出了2 种节流圈孔径下的激励水平，5.3、7.0 mm 孔径下激励器前稳态压力分别为4.31、4.36 MPa，前者工况小于后者，稳态流量为0.42、0.40 kg/s，前者工况大于后者，激励幅值大小关系与稳态流量一致，可见激励水平与稳态流量成正相关。因此，激励路稳态流量越大，激励幅值越大，可通过调整激励路节流圈3 来改变激励路稳态流量从而获得更高的激励幅值。

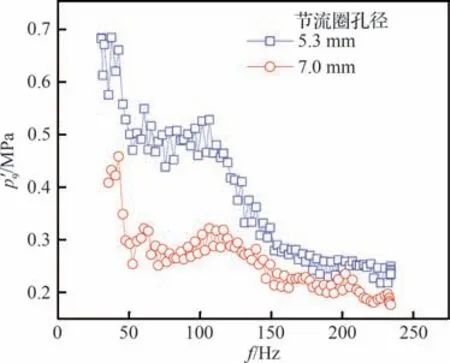
图8 激励路节流圈对激励水平的影响Fig. 8 Influence of throttle plate on excitation level in excitation circuit

2. 2 激励类型

在完成原试验件试验后，经特性分析得到产品大致改进方向，但由于试验件改进加工、试验系统搭建周期较长，因此既难以完成多种因素组合下大量产品的加工与试验，又无法及时、精确地预测结构优化后的产品性能。较试验而言，理论数值仿真可得到更多中间变量以及可更灵活地进行重要敏感因素分析，适合探索系统频率特性机理。因此，试验辅以仿真可使产品快速改进完成闭环迭代。此系统具有3 个边界，分别为贮箱、排放口与激励器，贮箱与主路排放口是比较明确的声学开端，激励源的类型与阻抗尚不明确。

系统频率特性仿真的首要任务是确定激励源即干扰施加类型，试验数据作为理论分析和数值模拟结果的校验标准，对于激励源类型分析具有直接参考价值。为判断激励源是属于流量脉动激励源还是压力脉动激励源，将激励器频率提高至670 Hz，得到长程激励试验数据，此时流量工况为7.82 kg/s。其中离激励源最近的2 处测点脉动压力幅值如图9 所示，可见在378 Hz 时p′9出现明显谐振峰，该频率是激励路这一局部系统的固有特性。从三通至激励源管长0.82 m，激励路管径为主路的2/5，则激励路管路特征阻抗为主路的6.25 倍，三通处主路可作为激励路的开端。若将激励源看作压力激励源端，此处压力脉动不受系统影响，认为是开开边界，计算获得一阶谐振频率为853 Hz；若将激励源看作流量激励源端，此处流量脉动不受系统影响，可认为是开闭边界，一阶谐振频率为427 Hz。考虑到三通处未达到绝对的开端条件，且激励路本身存在分支，带来部分柔性，可认为此激励源为流量激励源。此外，p′8也可表现出此频率，该测点处于信号传播至主路的途中，由于节流圈3 的衰减作用，在谐振峰附近的脉动压力信号衰减为p′9的41%，可见经过节流圈后的压力脉动表现出大幅衰减特点，可表明节流圈3 的隔绝作用。因此，可通过分析试验数据为数值模拟提供激励源这一边界条件类型。

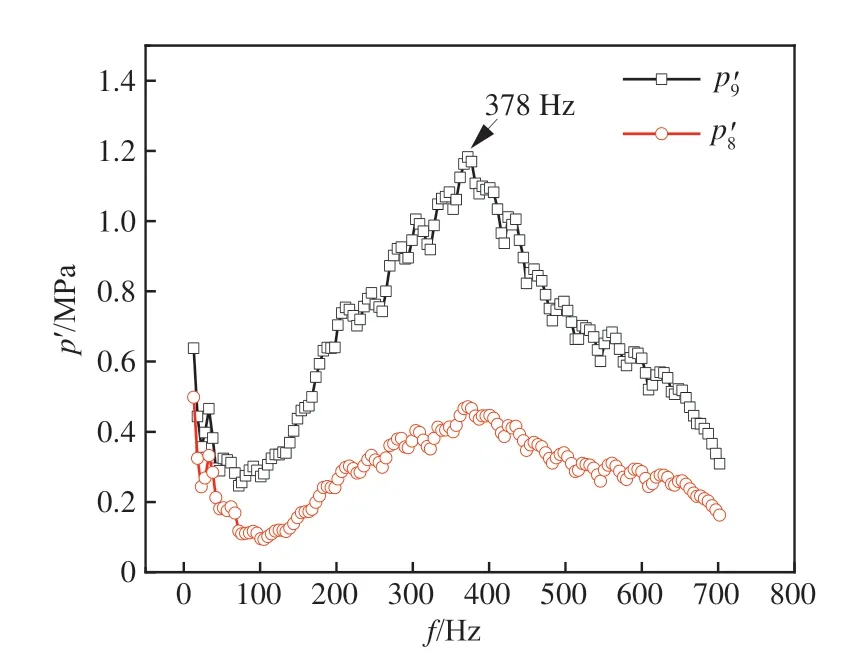
图9 长程激励试验的测点频谱数据Fig. 9 Spectrum data of measuring points in longrange excitation test

激励源阻抗可表征激励端边界条件，利用距激励源最近的测点p′9阻抗表征激励源阻抗，计算结果如图10 所示。可见，激励源阻抗在100 Hz的低频范围内，其值为实部与虚部大小相当的复阻抗；在＞100 Hz 的高频范围内，其值为虚部接近于0 MPa·s·kg-1，实部约为-0.8 MPa·s·kg-1的实阻抗。此试验值可作为数值计算的真实边界条件。

图10 激励源阻抗Fig. 10 Excitation source impedance

2. 3 激励隔离效果

进行数据处理时，需要保证激励源处的幅频特性受主路影响较小，此时可通过分析主路与激励路的脉动压力频率特性来研究隔离效果。图11 对比了p′9与p′6测点的脉动压力频率特性，其中p′9为激励源处脉动压力测点，p′6为主路试验件后处脉动压力。由p′9测点可见，整体上激励源处脉动压力幅值随频率变化。在100 Hz 以内，随着频率增加，幅值呈下降趋势，在35 Hz 和65 Hz 处表现出谐振峰，全系统的特性在此测点处也有体现；在100 Hz 以上，该测点表现出激励路的局部特征，由于扫频频率较低，未达到局部系统的一阶谐振频率，因此脉动幅值随着频率的增加而增加。由p′6测点可见，主路压力脉动幅值整体随着频率增加呈下降趋势，且在低频范围内下降较为明显，在整个频率段明显表现出全系统的谐振特征。另可见，高频段信号传播至主路时衰减较大，由于激励源处压力脉动幅值本身较高且呈增加趋势，因此，主路高频信号随频率增加而下降较为缓慢。通过分析可知，在75 Hz 以内，两测点谐振频率与幅值接近，即主路特性传播至激励路，主路对激励路的影响主要体现在小范围的低频段。＞75 Hz 时，激励源处测点主要表现出激励路的频率特征，幅值较大且整体呈上升趋势，无明显多阶谐振峰，主路整体表现为幅值较小的多阶谐振峰，与激励路谐振特征差别较大，可认为主路特性较少地传播至激励路。因此，在大部分频率范围内，激励源处的幅频特性受主路影响较小，即主路与激励路的隔离效果较好。

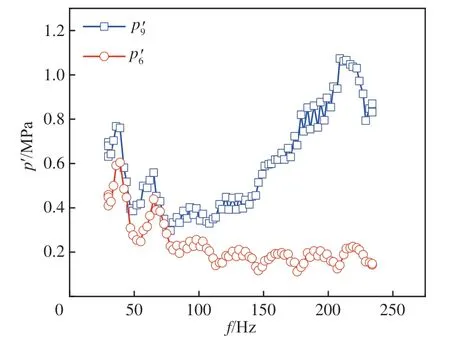
图11 部分脉动压力测点幅频特性Fig. 11 Amplitude-frequency characteristics of some pulsating pressure measuring points

2. 4 声学闭端效果

通常为了模拟声学闭端边界条件，其阻抗需远大于主管路的特征阻抗。如果采用设置纯节流元件措施，为了满足其阻抗2Δp/qm远大于主管路的特征阻抗a/A（a为声速，A为截面积），需要节流压降极大，可能会因为流阻过大，导致入口压力供应不足而限流，同时压降过大时容易汽蚀。因此，本试验采用一种特殊的声学闭端模拟装置，既能够实现声学闭端，又能降低管路的集中流阻，降低试验台压力供应要求。下面将对比以节流圈替代的无闭端装置与有闭端装置情况下的试验结果。

试验中，在5.91 kg/s 流量下，闭端装置压降为1.13 MPa。有/无闭端装置的实测压力脉动曲线如图12 所示，对应的流量工况分别为5.91 kg/s 与5.63 kg/s，其中p2、p′2测点为闭端装置后接近于激励源的测点，p1、p′1为闭端装置前接近于贮箱的测点。试验通过线性扫频完成，即随着时间增加，激励频率增加。通过时域试验数据图12（a）和图12（b）可见，相较于无闭端装置情况两测点脉动幅值相差较小，有闭端装置情况下p1测点脉动幅值明显小于p2测点。接下来分析有/无闭端装置情况下两测点分频值，如图12（c）和图12（d）所示。无闭端装置情况下，p′2测点较明显的谐振频率为47、111、150 Hz，p′1测点前三阶谐振频率分别为46、128、176 Hz；有闭端装置情况下，p′2测点较明显的谐振频率为42、58 Hz，p′1测点前三阶谐振频率分别为59、121、169 Hz。然而，有闭端装置情况下，两测点幅值随频率变化的差异性更大，可见该装置的存在使得闭端效果更好。

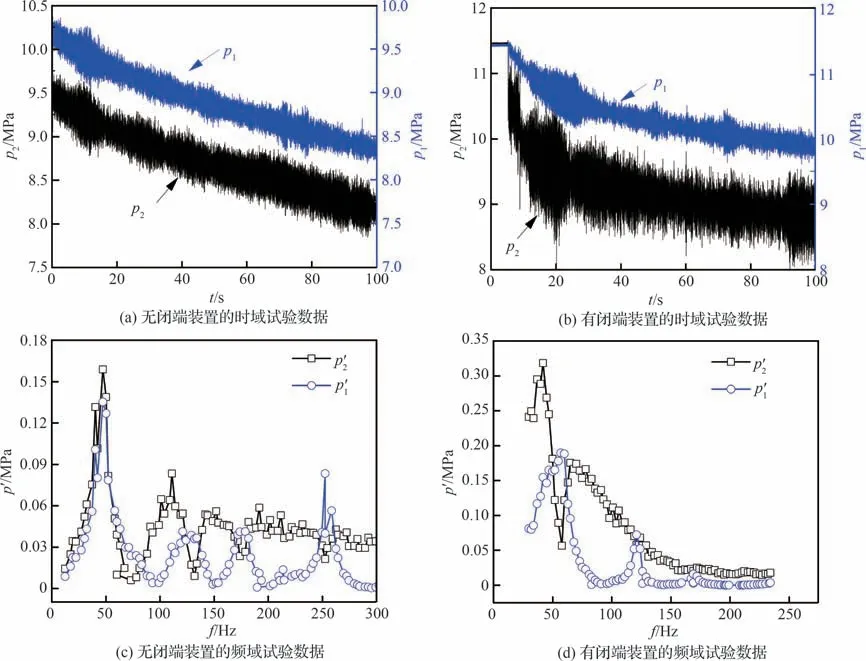
图12 有/无声学闭端装置下试验系统压力脉动幅值Fig. 12 Amplitude of pressure pulsation of test system with and without acoustic closed-end device

对于2 种结构状态，在小于一阶谐振频率附近的低频段，两测点的幅值皆较高，对低频信号的衰减效果较差。其中，p′1测点主要表征贮箱至闭端装置之间局部系统频率特性，由于闭端装置细管长的存在，理论上有闭端装置情况下的p′1测点谐振频率应低于无闭端装置情况。第二和第三阶频率符合此规律，第一阶谐振频率规律相反主要是由于闭端装置的低频闭端效果较差，主管路的低频特性会较大程度体现在p′1测点上，从而影响一阶频率规律。

再者，通过幅值衰减特性进一步分析闭端效果，有/无声学闭端装置前后两测点的压力脉动幅值比如图13 所示。以幅值比为1 对应的频率作为闭端装置是否起作用的频率点，将幅值比＜0.5的频率范围视为闭端效果较好的频率段。对于该试验系统而言，可认为无闭端装置的系统结构在82 Hz 以上能起到闭端作用，在87～116 Hz、140～165 Hz、185～230 Hz 处闭端效果较好。有闭端装置的系统结构在62 Hz 以上能起到闭端作用，在66～117 Hz、125～168 Hz、172～230 Hz 以及低频30～43 Hz 时效果良好。可见，声学闭端装置具有较高的频率选择性，有/无声学闭端装置闭端效果较好的频率段在研究频率（30～230 Hz）中的占比分别为49.5%和82.5%。闭端装置使闭端作用最低频率降低了25%，使闭端效果较好的频率范围增加了67%。在近乎相同工况下，增加声学闭端装置后，该装置上下游压力脉动幅值相差较大，衰减效果较好，具有更佳的闭端效果。

图13 声学闭端装置前后压力脉动幅值比Fig. 13 Amplitude ratio of pressure pulsation before and after acoustic closed-end device

有闭端装置情况下，闭端装置前后的压力脉动的衰减作用较强，且除谐振频率外，在更宽频率范围内p′2测点的压力脉动幅值远大于p′1测点。为验证声学闭端装置的闭端效果，可分析各阶谐振频率下直管段的压力振型，其中幅值极大值点为波腹，幅值极小值点为波节，且压力波腹位置可认为是良好的声学闭端。从图14 可见，除一阶、二阶振型变化较平缓外，p′2、p′3、p′4、p′5测点的压力脉动幅值明显依次降低，呈现出波腹-波节形式的1/4 波长振型，即靠近闭端装置的p′2测点处于压力波腹位置，说明闭端装置效果较好。试验中也发现在不同工况下，改进装置的闭端效果一致性较好，不受稳态流量工况影响。

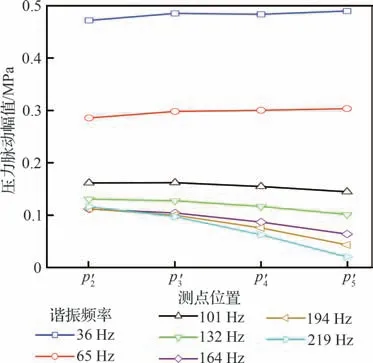
图14 直管段在各阶谐振频率下的振型Fig. 14 Mode shapes of straight pipe section at various resonant frequencies

2. 5 扫频策略影响

为分析扫频方式对液流激振试验数据的影响，对比阶梯扫频和线性扫频策略数据特征。阶梯扫频方式为1 s 均匀增加10 Hz，频率不变停留3 s；线性扫频方式为4 s 均匀增加10 Hz，不停留。理论上而言，理想的激励器控制系统须使系统产生具有足够定频维持时间的稳态振荡，在固定采样频率的时间分辨率下，能够使数据具有足够高的频率分辨率。因此，较为精确的扫频方式为阶梯扫频，但线性扫频具有数据易处理的优势，因此文中研究2 种扫频方式的数据区别。图15 为在2 种扫频方式下不同时间处所识别的振荡频率，对应流量工况为5.91 kg/s，其中线性扫频频率随时间线性增加，阶梯扫频准确数据分析应取停留3 s 内的定频激励，由于机械及电器惯性延迟存在，识别的真实频率在2 s 内能够保持定频。因此，取2 s 内频率停留平台处的幅值数据作为该频率下的准确幅值，此数据为“阶梯平台”，见图16。可见，由于阶梯扫频频率停留平台处能量几乎全部集中在该频率处，其幅值位于阶梯扫频锯齿状数据的尖峰处。对于线性扫频策略而言，在＜100 Hz 的低频范围内的识别幅值与阶梯平台处数据一致，＞100 Hz 时识别幅值相对较小。幅值较小是由于在数据分析的一个时间窗内系统参数振荡频率线性变化，部分能量会被识别频率附近其他频率带走，从而造成识别频率处幅值较低。然而，2 种扫频方式下识别出的系统谐振频率皆为 65 Hz，频率识别准确度一致。

图15 2 种扫频策略下识别频率随时间变化Fig. 15 Variation of recognition frequency with timefor two frequency sweep strategies

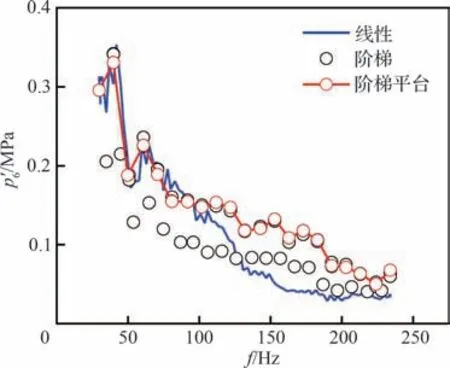
图16 不同扫频策略下的测点频谱数据Fig. 16 Spectrum data of measuring points for different frequency sweep strategies

2. 6 幅相特性分析

在压力脉动信号由激励路下游传播至主路上游的沿程途中，各测点的频率特征能反映出测点所在的局部子系统或全系统的频率特性，10.71 kg/s 流量工况下各个测点的幅频曲线如图17 所示。可见，脉动压力向上游传播过程中，脉动幅值整体呈现依次减小。p′9测点在37、65 Hz 处表现出极大值，高频段幅值随频率增加大幅升高，直至如图9 所示，在378 Hz 处出现幅值超过 1 MPa 的谐振峰，表现出激励路的局部特性。p′6、p′5、p′2这3 个测点表现出整个系统在贮箱入口、主路排放口、激励源3 个边界条件下的多阶谐振特征，各阶谐振频率为36、65、101、132、164、194、219 Hz，前三阶谐振频率对应幅值约分别为0.55、0.35、0.18 MPa，幅值随阶数增加依次降低。p′8测点整体谐振与p′6、p′5、p′2这3 个测点类似，呈现出整个系统的多阶谐振特征，不同的是受p′9测点影响，p′8测点高频段幅值随频率增加稍增大。可见，代表主系统的p′6、p′5、p′2测点与代表局部激励系统的p′9测点频率特性不同，而连接两部分系统的p′8测点表现出交叉特征。p′1测点频率特征与其他测点明显不同，表现出贮箱至闭端装置局部子系统的谐振特征，各阶谐振频率为57、123、169 Hz。此外，通过对比图16 中的线性扫频曲线与图17 的p′6测点，可明显看出随着稳态流量工况增加，幅值整体增加，且系统多阶谐振特征更加明显。

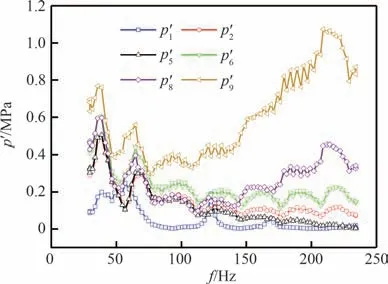
图17 测点的幅频曲线Fig. 17 Amplitude-frequency curves of measuring points

进一步分析流路中激励经过节流圈和三通前后以及直管沿程的相位关系，各个测点的绝对相位值受激励源初相位影响，利用测点之间的相位差可消除此影响，测点的幅值比与相位差如图18 所示。从整体可见，除个别谐振点外的其他频率处相位差为负值，说明激励从激励路—主路下游—主路上游传播过程中，整体呈现相位滞后的特点，也表现出谐振特征，但相位谐振频率与幅值谐振频率不一致。从图18（a）可看出，脉动信号经过激励路节流圈3 相位会产生较大变化，在100 Hz 以下，随频率增加，相位差绝对值增加，最大可达50°；在100 Hz 以上，相位差绝对值逐渐减小，最终趋于0°。在图18（b）中，脉动压力信号经过激励路与主路交界的三通后，相位差绝对值随着频率增加而增加，此相位差是由于较长的排放路引进了较大的惯性与容性，对相位差的影响最大可达100°，且p′6与p′8测点的幅值比也呈现出非1 的谐振特征。在图18（c）中，信号流经主路节流圈2，与图18（a）中所描述的经过激励路节流圈不同的是随着频率增加，相位差绝对值一直增加，在225 Hz 处达95°。从幅频曲线图17 可见激励路与主路频率特性的不同，因此节流圈相位差也呈现不同特征。可见，节流圈前后相位差与幅值相似，同样受局部子系统的影响。图18（d）给出了管路沿程幅值比与相位差，随着频率增加，幅值比越大，意味着直管段振型越明显，除前两阶谐振点附近外，其他频率点相位差绝对值＜10°。两测点距离为1.18 m，声速取为1 400 m/s。以100 Hz 为例，从行波观点分析，相位差应达到30.3°。以驻波观点来看，两测点相位差为0°。因此，液流激励系统处于驻波与行波叠加的状态。

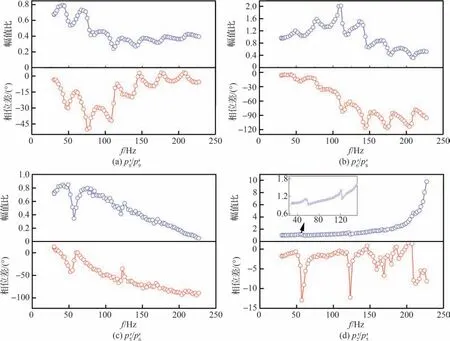
图18 幅值比与相位差随频率的变化Fig. 18 Variation of amplitude ratio and phase difference with frequency

3 结 论

为了探索试车中液体火箭发动机关键组件以及所在局部子系统的频率特性，本文利用地面液流激励试验模拟真实局部子系统的受迫振荡，获得的关于模拟供应系统频率特性的相关结论如下：

1） 在30～230 Hz 的研究频率范围内，激励源处可产生分频幅值为0.3～1.07 MPa 人工脉动压力信号。试验系统除主路较少低频特性传播至激励路外，大部分频率范围内皆表现为局部激励系统特性，即激励路受主路影响较小，具有较好的激励隔离效果。转盘式激励器为流量脉动型激励器，激励器的线性与阶梯扫频在识别频率方面并无差别，但在100 Hz 以上线性扫频识别幅值比阶梯扫频平台处的真实幅值小。

2） 声学闭端装置具有明显的频率选择性，当谐振频率高于二阶时，闭端装置后直管段振型在靠近闭端装置处表现出波腹特征。安装声学闭端装置的试验系统中，闭端效果较好的频率段在研究频率范围中的占比为82.5%，此措施使该频率段范围增加了67%，试验系统呈现出较良好的闭端边界。

3） 脉动压力向上游传播过程中，脉动幅值逆流向整体呈现依次减小趋势；随着稳态流量增加，脉动幅值增加，同时主系统多阶谐振频率特征更加突出；在下游激励时，主系统整体表现出以贮箱开端、主路排放开端以及激励源为边界的多阶谐振特征，谐振幅值随阶数增加而降低（前三阶谐振频率分别为36、65、101 Hz，幅值分别为0.55、0.35、0.18 MPa）。

4） 以大阻抗元件分割的两局部系统频率特性不同，而连接两局部系统的测点表现出交叉特征；在具有强边界的局部子系统内，重点表现此边界下的局部系统频率特性，该特性在其他局部子系统中表现较弱。例如，闭端装置前局部子系统前三阶谐振频率分别为57、123、169 Hz，激励器附近局部子系统谐振频率为378 Hz，明显与主系统谐振频率不同。

5） 对于该纯受迫激励系统，沿激励传播方向相位依次滞后，并在谐振点附近产生极值，脉动压力在节流圈以及带长支路的三通组件前后会形成较大相位差，最大可达-100°。从相位差可见，该液流激励系统处于驻波与行波叠加的状态。