贝叶斯统计中单参数后验分布的精确计算方法

党 红

（长治学院 数学系，山西 长治 046011）

1 引言

统计学界主要分为两大学派：经典统计学派和贝叶斯统计学派，两者的主要区别在于是否利用先验信息，主要分歧在于是否把总体中的未知参数看作是一个随机变量。

近年来，贝叶斯统计思想在不同的领域都得到了广泛的应用，2017年薛玲余研究了贝叶斯估计在教育学中的应用[1]，2017年钟建军等研究了贝叶斯统计在心理学上的应用[2]，2018年张翠玲，谭铁君研究了基于贝叶斯统计推理的法庭证据评价[3]，2012年王彩凤等研究了中国股市量价关系分析中的后验分布构造与模拟[4]。贝叶斯统计中一切统计推断都是基于后验分布来进行的，所以后验分布的重要性不言而喻。

2 后验分布的计算方法

2.1 直接计算后验分布

在一个单参数贝叶斯统计问题中，设X～p（x|θ），在获得样本X后，参数θ的后验分布即为给定X=x条件下θ的条件分布，记为π（θ|x）

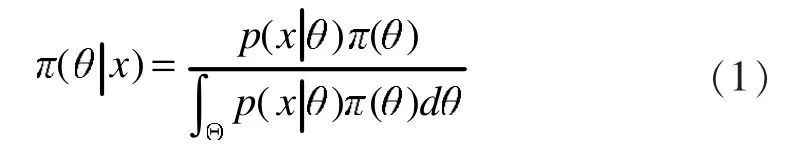
其中，p（x|θ）为样本 X 对应的总体分布，π（θ）为参数的先验分布。

当已获得样本为X1，X2，…Xn时，可以利用似然函数 L（x|θ）代替（1）式中的总体分布 p（x|θ）来计算后验分布，即

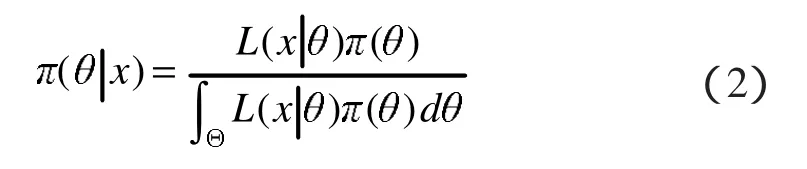
例 1 设 X|θ～B（n，θ），参数 θ服从均匀分布 U（0，1），求参数 θ的后验分布[5]。

解：因为 X|θ～B（n，θ），则其概率分布为

参数 θ的先验分布为 π（θ）=1，θ∈（0，1），故由后验分布

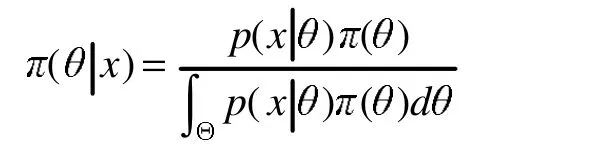
得到

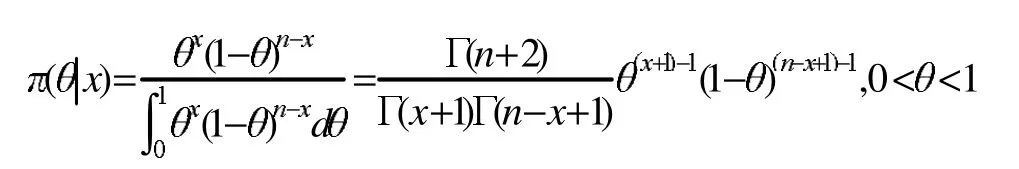
即，参数θ的后验分布为贝塔分布Be（x+1，n-x+1）

2.2 由后验分布的核计算后验分布

式（3）中，p（x|θ）π（θ）即可作为后验分布 π（θ|x）的核，左端和右端两式相差一个与参数θ无关的常数因子，将 p（x|θ）π（θ）正则化即可得到后验分布。

例 2 设 X|θ～N（θ，σ2），其中 σ2已知而 θ未知，参数 θ的先验分布为 N（μ，τ2），其中 μ 和 τ已知，求参数θ的后验分布[5]。

解：因为 X|θ～N（θ，σ2），则其概率密度为

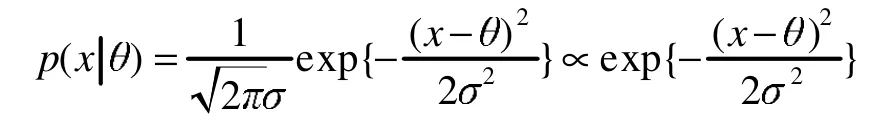
参数θ的先验密度为

则参数θ的后验密度

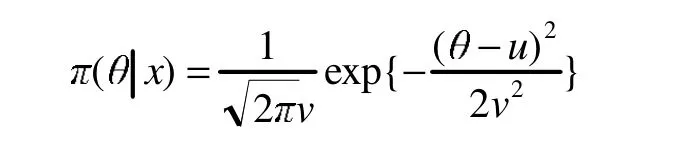
然而，常见的统计分布是非常有限的，式（3）中后验分布的核在针对较为常见的分布时才便于计算。

上述两种方法是仅有的针对单参数贝叶斯统计模型的精确后验分布的计算方法。由于常见的分布十分有限，精确计算方法在实际应用过程中具有局限性，这也是精确计算方法的主要缺点。

3 结束语

文章旨在为后验分布在实际应用中的计算提供理论基础，如果对后验分布计算中的要求精度不高的话，在后验分布计算方面还可以用利用R软件[6]、SPSS软件或Matlab软件做辅助工具，更有利于简化贝叶斯统计中后验分布的计算，这也是后续研究过程中需要注意的方向。